bzoj 3111: [Zjoi2013]蚂蚁寻路（DP）

3111: [Zjoi2013]蚂蚁寻路

题目描述 Description
在一个 n*m 的棋盘上，每个格子有一个权值，初始时，在某个格子的顶点
处一只面朝北的蚂蚁，我们只知道它的行走路线是如何转弯，却不知道每次转弯
前走了多长。蚂蚁转弯是有一定特点的，即它的转弯序列一定是如下的形式：
右转，右转，左转，左转，右转，右转…左转，左转，右转，右转，右转。
即两次右转和两次左转交替出现的形式，最后两次右转（最后两次一定是
右转）后再多加一次右转。我们还知道，蚂蚁不会在同一个位置连续旋转两次，
并且蚂蚁行走的路径除了起点以外，不会到达同一个点多次，它最后一定是回
到起点然后结束自己的行程，而且蚂蚁只会在棋盘格子的顶点处转弯。
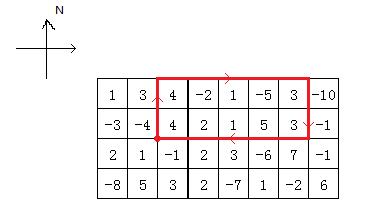
设 k为蚂蚁左转的次数除以2，当k=0 时，蚂蚁可能行走的路径如下图

转弯序列为：右转，右转，右转。
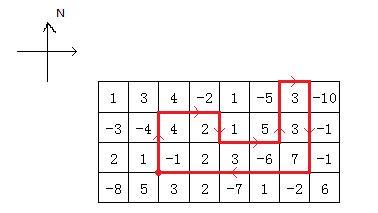
当 k=1 时，蚂蚁可能行走的路径如下图


转弯序列为：右转，右转，左转，左转，右转，右转，右转。
现在已知棋盘大小、每个格子的权值以及左转次数/2 的值，问蚂蚁走出
的路径围出的封闭图形，权值之和最大可能是多少。


输入描述 Input Description
在输入文件ant.in 中，第一行三个数n,m,k。意义如题目描述。
接下来一个n 行m 列的整数矩阵，表示棋盘。
输出描述 Output Description
一个数，表示蚂蚁所走路径围出的图形可能的最大权
值和。
样例输入 Sample Input
2 5 2
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
样例输出 Sample Output
-8
数据范围及提示 Data Size & Hint
【样例说明】
除了第一行的第二个和第一行的第四个都要围起来才至少合法。
【数据规模与约定】
10%的数据所有格子中权值均非负
另20%的数据n=2
另30%的数据k=0
100%的数据1≤n≤100,1≤m≤100,0≤k≤10 保证存在合法路径，数据有梯度，格子中每个元素的值绝对值不超过 10000

分析：

蚂蚁走的区域一定是以下形状：左边右边下面都是平的，上面凹凸不平，但一定是一凸一凹一凸一凹一凸……

就如样例的第二张图，可以理解为若干个矩形连在一起，底在一条线上，高h满足h1>h2<h3>h4<h5……

dp[i][j][x][p]表示当前是第k个矩形，右下角那个点在坐标(i, j)上，右上角那个点在坐标(x, j)上能包住的最大数字和

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
#define inf 1000000005
int a[102][102], sum[102][102], dp[102][102][102][22];
int main(void)
{
	int n, m, k, i, j, h, p, ans, now;
	scanf("%d%d%d", &n, &m, &k);
	k = k*2+1;
	for(i=1;i<=n;i++)
	{
		for(j=1;j<=m;j++)
			scanf("%d", &a[i][j]);
	}
	for(j=1;j<=m;j++)
	{
		for(i=n;i>=1;i--)
			sum[i][j] = sum[i+1][j]+a[i][j];
	}
	ans = -inf;
	memset(dp, -62, sizeof(dp));
	for(j=1;j<=m;j++)
	{
		for(i=1;i<=n;i++)
		{
			for(h=1;h<=i;h++)
			{
				if(j==1)
					dp[i][j][h][1] = sum[h][1]-sum[i+1][1];
				else
					dp[i][j][h][1] = max(dp[i][j-1][h][1], 0)+sum[h][j]-sum[i+1][j];
				if(k==1)
					ans = max(ans, dp[i][j][h][1]);
			}
		}
	}
	for(p=2;p<=k;p++)
	{
		for(j=1;j<=m;j++)
		{
			for(i=n;i>=1;i--)
			{
				if(p%2==0)
				{
					now = -inf;
					for(h=2;h<=i;h++)
					{
						now = max(now, dp[i][j-1][h-1][p-1]);
						dp[i][j][h][p] = max(dp[i][j-1][h][p], now)+sum[h][j]-sum[i+1][j];
						if(p==k)  ans = max(ans, dp[i][j][h][p]);
					}
				}
				else
				{
					now = -inf;
					for(h=i-1;h>=1;h--)
					{
						now = max(now, dp[i][j-1][h+1][p-1]);
						dp[i][j][h][p] = max(dp[i][j-1][h][p], now)+sum[h][j]-sum[i+1][j];
						if(p==k)  ans = max(ans, dp[i][j][h][p]);
					}
				}
			}
		}
	}
	//printf("%d\n", dp[5][4][3][3]);
	printf("%d\n", ans);
	return 0;
}
/*
5 5 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
*/