模型:
一个有向图G,设定一个点r,要求点r能到达G中所有的点,如果这样的点不存在,新建并向所有入度为0的点连边
支配点:
对于点u,如果在删掉点p之后,r不能到达u,那么称p(p!=u)点是u点的一个支配点,规定idom[u]为u点的最近支配点,注意r点可以是u点的最近支配点
支配树:
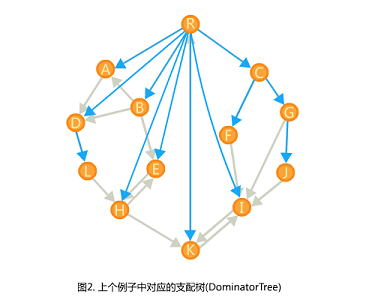
r为根,所有的idom[u]向u连一条边,可以形成一棵树
很好发现:①idom[u]是u的父亲,②从根到u上的所有点都是u的支配点
引用一张图:
主要问题:如何求出支配树
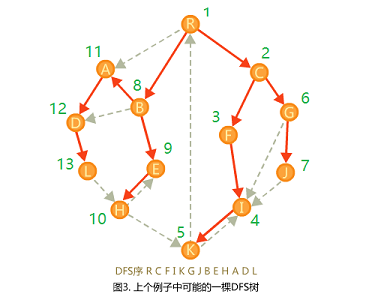
先求出DFS树和DFS序,如上图:
设dfn[x]为x点的dfs序,有
半支配点:若u是v的祖先,且存在一条u到v的路径,路径上所有点i(i!=u && i!=v)都满足dfn[i]>dfn[v],那么称u点是v点的一个半支配点(相当于从u到v有两条完全独立,没有交点的路径,或者u是v的父亲,例如图中的8->12,2->6->4),规定sdom[u]为dfn[]最小的半支配点
性质①:若dfn[u]<dfn[v],那么u点到v点的所有路径一定都经过u和v的最近公共祖先
性质②:对于除了r以外的所有点x,在DFS树中,idom(x)和sdom(x)一定都是x的祖先(不包括x),并且idom(x)一定是sdom(x)的祖先(包括sdom(x),也就是说可能idom(x)==sdom(x))
性质③:对于DFS树上两点x和y,如果x是y的祖先,要不idom(y)在x->y这条路径上,要不idom(y)是iodm(x)的祖先(当然可能idom(y)==iodm(x))
定理①:对于DFS树上某点x,如果从sdom(x)到x的这段路径上(不包括sdom(x),包括x)所有点i都满足sdom(i)也在这个路径上(包括sdom(x)),那么idom(x)=sdom(x)
定理②:对于DFS树上某点x,定义从sdom(x)到x的这段路径上(不包括sdom(x),包括x)所有点i中dfn[sdom(i)]最小的那个点是y,如果sdom(y)==sdom(x),那么idom(x) = sdom(x),否则idom(x) = idom(y)
其实定理②已经包含定理①了
Lengauer-Tarjan算法:
步骤①输入,如果入度为0的点不止一个,新建一个节点r连向所有入度为0的点,将其作为支配树的根
G[]:有向图; Gp[]:G[]的反向图
in[x]:x点的入度
步骤②DFS一遍求出DFS序和DFS树,并用DFS序对每个点重新标号
dfn[x]:x点的dfs序
rak[cnt]:dfs序为cnt的是几号点
fa[x]:DFS树中x节点的父亲
步骤③求出所有的sdom()
val[k]:k是点,val[k]也是点,具体用途看下面:
sdom[u]:u点的最小半支配点
初始化sdom[x] = x,val[x] = x
一个点u的sdom有两种情况:
1. sdom[u] = fa[u];
2. 若dfn[v]>dfn[u],且v的某个子孙x满足x到u在原图中有一条边,那么sdom[u] = min(sdom[u], sdom[v])
翻译过来就是:若dfn[x]>dfn[u],且x到u有一条非树边,那么x到(x,u)最近公共祖先(不包括祖先)这段链上所有点的sdom[]都一定是u点的半支配点
那可以从dfs[]最大的点开始遍历,对于当前点u,遍历原图中所有与u的前驱k,
sdom[u] = min(sdom[val[k]] (k为u的所有前驱))
很显然k只有两种情况:
1. k点是u点的父亲,这时val[k] = k且sdom[k] = k刚好是上面sdom[]的第一种情况;
2. k点满足dfn[k]>dfn[u],这时只要能够快速查找k到(k,u)最近公共祖先这段链上所有点sdom[]值最小的那个点val[k]即可!主要是如何快速求出k到u这段链上所有点sdom[]值最小的那个,也就是快速求确定所有点的val[],其中val[]还会因当前u点的不同而改变,这里可以用带权并查集实现
举个例子:还是这张图
假设当前u遍历到了4,枚举点4的所有前驱(k = 3, 6, 7)
k = 3时,点3还没被遍历,并且正好是4点的父亲,sdom[4] = sdom[val[3]] = sdom[3] = 3
然后k = 6,点6已经被遍历,根据上面红色粗斜体可得val[6] = 6,这时有sdom[4] = min(3, sdom[val[6]]) = 2
然后k = 7,点7已经被遍历,依旧可得val[7] = 6,这时有sdom[4] = min(3, sdom[val[7]]) = 2
得出sdom[4] = 4,具体遍历下一个点3
步骤④根据上面的定理,求出所有点的idom[]
Sp[]:Sp[x]中存的所有点i,都满足sdom[i] = dfn[x]
再回顾下那个定理:从sdom(x)到x的这段路径上(不包括sdom(x),包括x)所有点i中dfn[sdom(i)]最小的那个点是y,如果sdom(y)==sdom(x),那么idom(x) = sdom(x),否则idom(x) = idom(y)
注意上面的红色部分!它正好是带权并查集所维护的,也就是说,如果当前u遍历到了sdom[v]的儿子,所有点i中dfn[sdom(i)]最小的那个正是点val[v]!这时直接判定就好了!
可是当sdom[val[v]]!=sdom[v]时,你不能直接idom[v] = idom[val[v]],因为val[v]点的idom[]值可能还未求出
那么就暂时idom[v] = val[v],等处理完毕之后,遍历所有点(注意这个是原标号!),若idom[p]!=rak[sdom[p]],就让idom[p] = idom[idom[p]];
步骤⑤构造支配树
到这一步就简单了,所有的idom[i]到i连一条边,最后形成的就是如假包换的支配树
不过sdom[]存的不是原标号,可以恢复原标号(也可以不管它了反正没用了)
支配树模板:
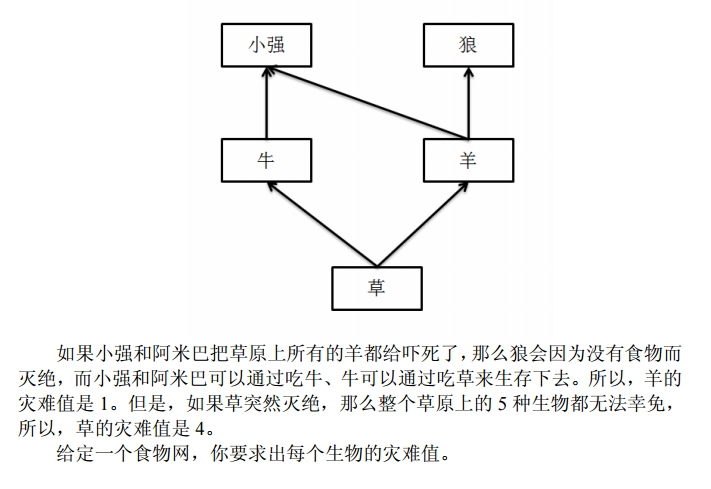
支配树裸题
A吃B,那么B到A连一条有向边,之后求出支配树
每个节点的答案就是支配树中以当前节点为根的子树大小-1
#include<stdio.h>
#include<vector>
using namespace std;
int dfn[200005], rak[200005], fa[200005], sdom[200005], idom[200005];
int n, cnt, ufs[200005], val[200005], size[200005], in[200005];
vector<int> G[200005], Z[200005], Gp[200005], Sp[200005];
int Find(int p)
{
int r;
if(ufs[p]==p)
return p;
r = Find(ufs[p]);
if(sdom[val[ufs[p]]]<sdom[val[p]])
val[p] = val[ufs[p]];
return ufs[p] = r;
}
void Sech(int p)
{
int i, v;
sdom[p] = dfn[p] = ++cnt;
rak[cnt] = p;
for(i=0;i<G[p].size();i++)
{
v = G[p][i];
if(dfn[v]==0)
{
Sech(v);
fa[v] = p;
}
}
}
void Sech2(int u)
{
int i, v;
size[u] = 1;
for(i=0;i<Z[u].size();i++)
{
v = Z[u][i];
Sech2(v);
size[u] += size[v];
}
}
int main(void)
{
int i, x, p, j, k, v;
scanf("%d", &n);
n += 1;
for(i=1;i<=n;i++)
{
dfn[i] = in[i] = 0;
ufs[i] = val[i] = i;
Gp[i].clear();
Sp[i].clear();
Z[i].clear();
}
for(i=1;i<=n-1;i++)
{
while(scanf("%d", &x), x!=0)
{
G[x].push_back(i);
Gp[i].push_back(x);
in[i]++;
}
}
for(i=1;i<=n-1;i++)
{
if(in[i]==0)
{
G[n].push_back(i);
Gp[i].push_back(n);
}
}
Sech(n);
for(i=n;i>=2;i--)
{
p = rak[i];
for(j=0;j<Gp[p].size();j++)
{
k = Gp[p][j];
/*if(dfn[k])
{*/
Find(k);
sdom[p] = min(sdom[p], sdom[val[k]]);
//}
}
ufs[p] = fa[p];
Sp[rak[sdom[p]]].push_back(p);
for(j=0;j<Sp[fa[p]].size();j++)
{
v = Sp[fa[p]][j];
Find(v);
if(sdom[val[v]]==sdom[v])
idom[v] = rak[sdom[v]]; //同理:idom[v] = fa[p];
else
idom[v] = val[v];
}
Sp[fa[p]].clear();
}
for(i=1;i<=n;i++)
{
p = rak[i];
if(idom[p]!=rak[sdom[p]])
idom[p] = idom[idom[p]];
}
/*for(i=2;i<=n;i++)
{
p = rak[i];
sdom[p] = rak[sdom[p]];
}*/
for(i=1;i<=n-1;i++)
Z[idom[i]].push_back(i);
Sech2(n);
for(i=1;i<=n-1;i++)
printf("%d\n", size[i]-1);
return 0;
}
/*
13 21
1 2 11 12 7 4
2 3 12 13 6 4
3 4 1 11
4 5 8 12
2 6 13 10
6 7 10 9
1 8 10 5
8 9 5 1
9 10 5 4
8 11
5 5
1 2
2 3
3 4
4 5
5 1
5
0
1 0
1 0
2 3 0
2 0
*/
























 1016
1016

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








