DAY14.
我不想过那种一眼望得到头的人生,所以我努力摆脱困境。
二重积分
二重积分的例题一般要求你求平面区域的面积
所以这里就分两种坐标计算的题型
- 平面直角坐标
I = ∬ D f ( x , y ) d x d y I = \iint_D f(x,y)d_xd_y I=∬Df(x,y)dxdy
X型区域:
I
=
∫
a
b
d
x
∫
y
1
(
x
)
y
2
(
x
)
f
(
x
,
y
)
d
y
I = \int_a^{b} d_x \int_{y_1(x)}^{y_2(x)} f (x,y)d_y
I=∫abdx∫y1(x)y2(x)f(x,y)dy
Y型区域:
I
=
∫
a
b
d
y
∫
x
1
(
y
)
x
2
(
y
)
f
(
x
,
y
)
d
x
I = \int_a^{b} d_y \int_{x_1(y)}^{x_2(y)} f (x,y)d_x
I=∫abdy∫x1(y)x2(y)f(x,y)dx
- 极坐标系
I = ∫ α β d θ ∫ φ 1 ( θ ) φ 2 ( θ ) f ( ρ cos θ , ρ sin θ ) ρ d ρ I = \int_{\alpha}^{\beta} d_{\theta} \int_{\varphi_1 (\theta)}^{\varphi_2 (\theta)} f(\rho \cos \theta, \rho \sin \theta)\rho d_\rho I=∫αβdθ∫φ1(θ)φ2(θ)f(ρcosθ,ρsinθ)ρdρ
注意不要忘记极坐标里面最后那个 ρ \rho ρ
在计算的时候要注意这么几点:
1) 划分的区域D要简单,越简单越好
2)如果D和圆有关,
f
(
x
,
y
)
与
x
2
+
y
2
,
y
x
,
x
y
f(x,y) 与 x^2 + y^2 , \frac{y}{x},\frac{x}{y}
f(x,y)与x2+y2,xy,yx 有关,我们解题一般使用极坐标
3)要特别注意是否可以使用对称性来解题。
若D关于 x 轴对称,记 x 轴以上的区域为 D 1 D_1 D1
有: ∬ D f ( x , y ) d σ = 0 \iint_D f(x,y) d_\sigma = 0 ∬Df(x,y)dσ=0 其中 f 为奇函数; S = 2 ∬ D 1 f ( x , y ) d σ S = 2\iint_{D1} f(x,y) d_\sigma S=2∬D1f(x,y)dσ 其中f为偶函数
例题
- 求 ∬ D ( 3 x + 2 y ) d x d y , D 是 由 x + y = 2 , x = 0 , y = 0 \iint_D (3x+2y) d_xd_y,D是由 x+y = 2, x=0,y=0 ∬D(3x+2y)dxdy,D是由x+y=2,x=0,y=0所围成的图形。
解:积分区域如图所示
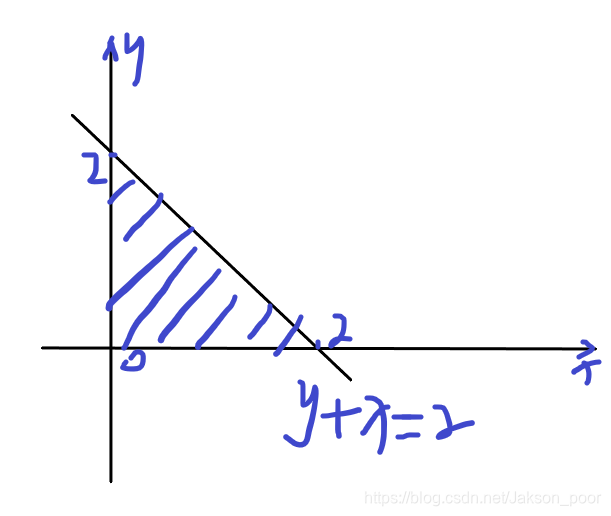
I = ∬ D ( 3 x + 2 y ) d x d y I = \iint_D (3x+2y) d_xd_y I=∬D(3x+2y)dxdy
选用x型区域积分
= ∫ 0 2 d x ∫ 0 2 − x ( 3 x + 2 y ) d y = \int_0^{2} d_x \int_0^{2-x} (3x+2y)d_y =∫02dx∫02−x(3x+2y)dy
= ∫ 0 2 3 x y + y 2 ∣ 0 2 − x d x = \int_0^{2} 3xy + y^2 |_0^{2-x} d_x =∫023xy+y2∣02−xdx
= 20 3 =\frac{20}{3} =320
- 将 I = ∫ 0 1 d x ∫ 0 x 2 f ( x , y ) d x d y I = \int_0^1 d_x \int_0^{x^2} f(x,y) d_xd_y I=∫01dx∫0x2f(x,y)dxdy化成极坐标
先画出被积区域如图:

化成极坐标为:
选用y型区域,穿入线为 y = x 2 , 穿 出 线 为 x = 1 y = x^2, 穿出线为 x = 1 y=x2,穿出线为x=1,将这两条线化为极坐标形式即为 ρ \rho ρ的被积函数。
I = ∫ 0 π 4 d θ ∫ tan θ sec θ sec θ f ( ρ cos θ , ρ sin θ ) ρ d ρ I = \int_0^{\frac{\pi}{4}} d_\theta \int_{\tan \theta \sec \theta}^{\sec \theta} f(\rho \cos \theta,\rho \sin \theta) \rho d_\rho I=∫04πdθ∫tanθsecθsecθf(ρcosθ,ρsinθ)ρdρ
- 求 I = ∬ D ( x 2 + y 2 + 3 x − 6 y + 9 ) d σ I = \iint_D (x^2 + y^2 + 3x -6y +9) d_\sigma I=∬D(x2+y2+3x−6y+9)dσ
其中D为半径为R的圆:

解: 因为 D D D关于X轴Y轴对称
所以 ∬ D 3 x d σ = 0 , ∬ D − 6 y d σ = 0 \iint_D 3x d_\sigma = 0, \iint_D -6y d_\sigma = 0 ∬D3xdσ=0,∬D−6ydσ=0
其中3x是关于x轴的奇函数, -6y是关于y轴的奇函数
则: I = ∫ 0 2 π d θ ∫ 0 R ρ 2 ρ d ρ I = \int_0^{2 \pi} d_\theta \int_0^{R} \rho^2 \rho d_\rho I=∫02πdθ∫0Rρ2ρdρ = π 2 R 4 + 9 π R 2 = \frac{\pi}{2} R^4 + 9\pi R^2 =2πR4+9πR2

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








