密码学 - AES 对称加密算法原理及原生实现

一. 概述

美国政府在 1997 年 9 月 12 日公开征集更高效更安全的替代 DES 加密算法，第一轮共有 15 种算法入选，其中 5 种算法入围了决赛，分别是 MARS，RC6，Rijndael，Serpent 和 Twofish。又经过 3 年的验证、评测及公众讨论之后 Rijndael 算法最终入选。

Rijndael 算法之所以最终能够被选为AES的原因是其安全、性能好、效率高、实用灵活。

Rijndael 算法支持多种分组及密钥长度，介于 128-256 之间所有 32 的倍数均可，最小支持 128 位，最大 256 位，而 AES 标准支持的分组大小固定为 128 位，密钥长度有 3 种选择：128 位、192 位及 256 位。

二. AES 算法的数学基础

Rijndaels 算法中的许多运算是按字节和 4 字节长的字来定义的。把一个字节看成是在有限域 GF(28) 上的一个元素。有限域（Finite Field）又名伽罗瓦域（Galois field），简单言之就是一个满足特定规则的集合，集合中的元素可以进行加减乘除运算，且运算结果也是属于此集合。

1. 有限域

AES的基础域是有限域 GF(28)

• 一个字节的全体 256 种取值构成一个 GF(28)
• 一个 GF(2) 上的 8 次既约多项式可生成一个 GF(28)
• GF(28) 的全体元素构成加法交换群、线性空间。
• GF(28) 的非零元素构成乘法循环群。

2. AES 在有限域上的表示

有限域 GF(28) 上的元素有多种表示方法，为了方便，Rijndaels 算法采用多项式表示法，下面是与还表示方法相关的几个定义

定义 1 : 一个由比特位 b7b6b5b4b3b2b1b0 组成的字节可表示成系数为 (0, 1) 的二进制多项式：b7X7 + b6X6 + b5X5 + b4X4 + b3X3 + b2X2 + b1X + b0

例：例：字节57＝01010111的多项式表示为:

定义 2 : 在 GF(28) 上的加法定义为二进制多项式的加法，其系数按位模 2 加。

例： 57＋83＝D4 等价于

定义 3 : 在 GF(28) 上的乘法定义为二进制多项式的乘积模一个次数为8的不可约多项式

其系数的十六进制表示为 11B，例： 57×83＝C1 等价于

定义 4 : 在 GF(28) 中，二进制多项式 b(x) 满足乘法逆为式a(x)b(x) mod m(x) = 1的二进制多项式。

定义 5 : 在 GF(28) 中，倍乘函数 xtime(b(x)) 定义为x·b(x) mod m(x)。具体的运算规则是：把字节B左移一位，若 b7=1， 则减去 m(x)，而在 GF(28) 上加减法等价，即加上 m(x)。例：

3. AES 的字表示与运算

3.1. 字表示

AES 数据处理的单位是字节和字，一个字由四个字节组成，表示为系数取自 GF(28) 上的次数低于 4 次的多项式，例如: 字57 83 4A D1等价于

3.2. 字运算

字运算是基于上述关于 AES 在 GF(28) 中的运算规则的。

字加法 ： 两多项式系数按位模 2 加

字乘法 ： 设 a 和 c 是两个字， a(x) 和 c(x) 是其字多项式， AES 定义 a 和 c 的乘积 b 为

如：设 a(x)、c(x) 和 b(x) 分别分别如下面（图 2-1）中所示， 由 b(x) = a(x)c(x) mod x4+1 得（图 2-1）表达式组

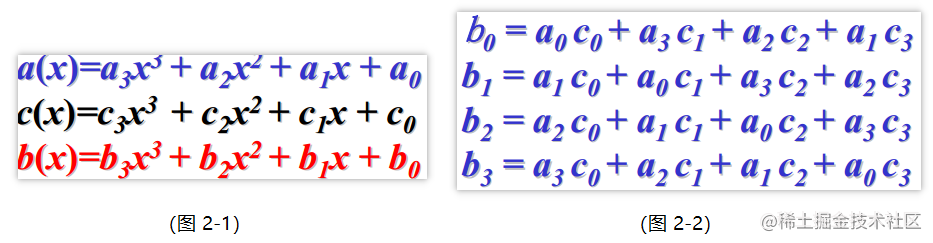
写成矩阵形式如下面的（图 2-3）所示，x4+1 是可约多项式，字 c(x) 不一定有逆，但 AES 选择的 c(x) 有逆，

从而使得 b(x) 的表达式可以使用上面（图 2-4）的矩阵表示，从而使得下面的MixColumns变换变为矩阵的乘法运算。

字 x 乘法 ：

矩阵形式如下图所示，因为模 x4+1，字 x 乘法相当于按字节循环移位

三. AES 的加密过程

1. 状态

在 AES 中除了字节和字外，还有一种被称为状态的数据处理方式，它用来存储加解密过程中的中间数据，一般用以字节为元素的矩阵或二维数组表示。

如果用 Nb 代表明密文所含的字数。 Nk 代表密钥所含的字数。 Nr 代表迭代轮数，则当 Nb 和 Nk 都等于 4 时的状态与密钥数组分别如下面的（图 3-1）和（图 3-2） 所示

根据 Rijndael 算法的定义，加密轮数会针对不同的分组及不同的密钥长度选择不同的数值

2. 加密过程概述

AES 加密算法的主要步骤有

• 轮密钥生成
• 初始轮密钥加变换：将最初的第一个（Nk 个字长）轮密钥亦即主密钥与初始状态进行比特位异或操作
• 标准轮（前 9, 11 或 13 轮）变换：
  • S 盒变换
  • 行移位变换
  • 列混合变换
  • 轮密钥加变换
• 最后一轮（第10, 12 或 14 轮）变换
  • S 盒变换
  • 行移位变换
  • 轮密钥加变换

3. AES 有限域上的加法

/**
 * 有限域GF(2)上的加法，<tt>modeSize</tt>位的异或操作
 * xor corresponding byte in two state arrays
 * @param first first operand
 * @param second second operand
 * @return xor result
 */
private short[][] xor(short[][] first, short[][] second) {
    short[][] result = new short[first.length][4];
    int length = first.length;
    for (short i = 0; i < length; i++) {
        for (short j = 0; j < length; j++) {
            result[i][j] = (short) (first[i][j] ^ second[i][j]);
        }
    }
    return result;
} 

4. 轮密钥生成 （GenerateRoundKeys）

轮密钥根据密钥产生算法通过主密钥得到。密钥产生分两步进行：密钥扩展和轮密钥选择，且郡守以下规则：

• 轮密钥的比特总数为明文数据块长度与轮数加 1 的积。例如，对于 128 位的分组长度和 10 轮迭代，轮密钥长度为 128 x (10 + 1) = 1408 位，即 11 个状态长
• 首先将用户密钥扩展为一个扩展密钥
• 再从扩展密钥中选出轮密钥：第一个轮密钥由扩展中的前Nb个字组成（即原主密钥），第二个轮密钥是接下来的 Nb 个字，以此类推。

4.1. 密钥扩展

用一个字元素的一维数组 W[Nb*(Nr+1)] 表示扩展密钥。把密钥放在该数组最开始的 Nk 个字中，其它的字由它前面的字经过处理后得到。分 Nk ≤ 6 和 Nk > 6 两种密钥扩展算法：

① Nk ≤ 6的密钥扩展

• 最前面的 Nk 个字是由主密钥填充
• 之后的每一个字 W[j] 等于前面的字 W[j-1] 与 Nk 个位置之前的字 W[j-Nk] 的异或
• 而且对于 Nk 的整数倍的位置处的字，在异或之前，对 W[j-1] 进行 Rotl 变换和 ByteSub 变换，再异或一个轮常数 Rcon 。

Rotl 是一个字里的字节循环左移函数， 设 W ＝（A， B， C， D） ， 则 Rotl(W) ＝ (B， C， D， A)。 „ 轮常数Rcon 与 Nk 无关，且定义为：

• Rcon[i] = (RC[i], ‘00’， ‘00’， ‘00’)，
• RC[0] = ‘01’，
• RC[i] = xtime(RC[i-1])

② Nk > 6 的密钥扩展

与 Nk ≤ 6 的密钥扩展相比， Nk > 6 的密钥扩展的不同之处在于：如果 j 被 Nk 除的余数＝4，则在异或之前，对 W[j-1]进行 ByteSub 变换。

增加 ByteSub 变换，是因为当 Nk > 6 时密钥很长，仅仅对 Nk 的整数倍的位置处的字进行 ByteSub 变换，就显得 ByteSub 变换的密度较稀，安全程度不够强。

4.2. 轮密钥的选择

根据分组的大小，依次从扩展密钥中取出轮密钥。 前面的 Nb 个字作为轮密钥 0，接下来的 Nb 个字作为轮密钥 1，以此类推

4.3. 代码实现

/**
 * 轮密钥扩展：将1个状态长度的主密钥扩展成<tt>rounds + 1</tt>个状态长度的轮密钥数组
 * generation of round keys
 * @param originalKey original cipher key
 * @return round keys
 */
private short[][] generateRoundKeys(short[][] originalKey) {
    short[][] roundKeys = new short[44][4];
    int keyWordCount = originalKey.length;
    // 1. copy the original cipher words into the first four words of the roundKeys
    System.arraycopy(originalKey, 0, roundKeys, 0, keyWordCount);
    // 2. extension from previous word
    for (int i = keyWordCount; i < keyWordCount * 11; i++) {
        short[] temp = roundKeys[i - 1];
        if (i % keyWordCount == 0) {
            temp = xor(substituteWord(leftShift(temp)), AESConstants.R_CON[i / keyWordCount]);
        }
        roundKeys[i] = xor(roundKeys[i - keyWordCount], temp);
    }
    return roundKeys;
} 

5. AES 基本变换

5.1. S 盒变换

一种作用在状态中每一个字节上的非线性变换，对比于 DES

• 因为 AES-126 明文数据块为 16 个字节，所以 AES 使用 16 个相同的S盒(其实是可重复 16 次使用同一个)； DES 使用 8 个不相同的S盒。
• AES 的 S 盒有 8 位输入 8 位输出，是一种非线性置换；DES 的 S 盒有 6 位输入 4 位输出，是一种非线性压缩。

AES 的 S 盒变换可按以下两步进行：

• 将输入字节用其 GF(28) 上的逆来代替
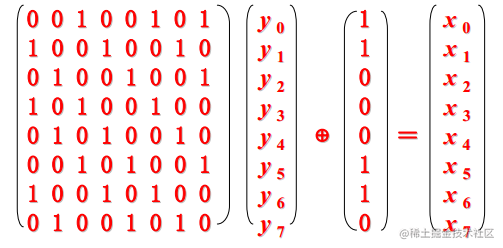
• 对上面的结果作如下的仿射变换： （以 x0－ x7 作输入，以 y0－ y7 作输出）

需要注意的是：

• S 盒变换的第一步是把字节的值用它的乘法逆来代替， 是一种非线性变换。
• 第二步是仿射运算，是线性变换。
• 由于系数矩阵中每列都含有 5 个 1，这说明改变输入中的任意一位，将影响输出中的5位发生变化。
• 由于系数矩阵中每行都含有 5 个 1，这说明输出中的每一位，都与输入中的 5 位相关。

代码实现

通过建表查表代替运算，同时将该操作拆分为substituteState、substituteWord和substituteByte三个子操作

实现 S 盒最快的方法就是，直接算出 S 盒的变换结果并造表存储，使用时直接查表（表大小为 256 个字节）。查表的方法是：取一个字节的高低 4 位分别作为行号和列号，通过行列号定位到的表中的元素即为新的替代字节。如下图左表中的 d4，

使用代码实现这一过程

/**
 * 状态替代：对状态中的每个字进行字替代
 * substitute value of a state array using byte as unit
 * @param state state array to be substituted
 * @return substitution result, a new state array
 */
private short[][] substituteState(short[][] state, short[][] substituteTable) {
    for (int i = 0; i < state.length; i++) {
        for (int j = 0; j < 4 ; j++) {
            state[i][j] = substituteByte(state[i][j], substituteTable);
        }
    }
    return state;
}

/**
 * 字替代：对字中每个字节进行字节替代
 * substitute all bytes in a word through SBox
 * @param aWord a word, aka 4 bytes
 * @return substitution result, a new and disrupted word
 */
private short[] substituteWord(short[] aWord) {
    for (int i = 0; i < 4; i++) {
        aWord[i] = substituteByte(aWord[i], AESConstants.SUBSTITUTE_BOX);
    }
    return aWord;
}

/**
 * 字节替代： 取一个字的高四位和低四位分别作为S盒的行号和列号，
 *          通过行列号取S盒中的字节替代原字节
 * substitute value of a byte through <tt>SBox</tt>
 * @param originalByte byte to be substituted
 * @return substitution result, a new byte
 */
private short substituteByte(short originalByte, short[][] substituteTable) {
    // low 4 bits in originByte
    int low4Bits = originalByte & 0x000f;
    // high 4 bits in originByte
    int high4Bits = (originalByte >> 4) & 0x000f;
    // obtain value in <tt>AESConstants.SUBSTITUTE_BOX</tt>
    return substituteTable[high4Bits][low4Bits];
} 

5.2. 行移位变换

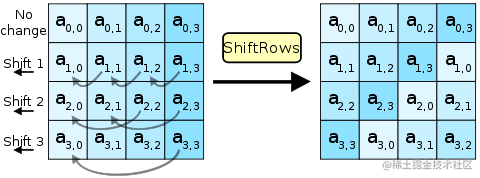
行移位变换对状态的行进行循环移位。 第 0 行不移位，第 1 行移 C1 字节， 第 2 行移 C2 字节， 第 3 行移 C3 字节。C1， C2， C3 按下表取值:

行移位变换属于置换，属于线性变换，本质在于把数据打乱、重排，起扩散作用。

代码实现

/**
 * 行移位变换：对状态的行进行循环左移，左移规则在<tt>shiftingTable</tt>中定义
 * row shifting operation, rotate over N which is defined in
 * <tt>AESConstants.SHIFTING_TABLE</tt> bytes of corresponding rows
 * @param state state array of the original plaintext
 * @return a new state array
 */
private static short[][] shiftRows(short[][] state, short[][] shiftingTable) {
    short[][] result = new short[state.length][4];
    for (int j = 0; j < 4; j++) {  // local byte in a word
        for (int i = 0; i < state.length; i++) {  // local word
            result[i][j] = state[shiftingTable[i][j]][j];
        }
    }
    return result;
} 

5.3. 列混合变换

列混合变换把状态的列视为 GF(28) 上的多项式 a(x)， 乘以一个固定的多项式 c(x)， 并模 x4+1:

需要注意的是：

• 列混合变换属于线性变换，起扩散作用。
• c(x) 与 x4 + 1 互素，从而保证 c(x) 存在逆多项式 d(x), 而 c(x)d(x) = 1 mod x4 + 1 。 只有逆多项式 d(x) 存在，才能正确进行解密

代码实现

/**
 * 列混合变换：状态数组与多项式等价矩阵进行有限域GF(2)上的矩阵乘法
 * @param state 状态数组
 * @param table 多项式等价矩阵
 * @return 列混合变换后的新状态
 */
private short[][] mixColumns(short[][] state, short[][] table) {
    short[][] result = new short[state.length][4];
    for (int i = 0; i < state.length; i++) {
        result[i] = matrixMultiply(state[i], table);
    }
    return result;
}

/**
 * 一个字与多项式等价数组在有限域GF(2)上的乘法操作
 * multiplication between a word of a state and a irreducible
 * polynomial <tt>C(x)=03x^3+01x^2+01^2+01x+02</tt> which is replaced as a
 * constant table <tt>AESConstants.CX</tt>
 * (aes-128: 4x4 x 4x1 = 4x1)
 * @param aWord a word of a state
 * @return multiplication result, a new word
 */
private short[] matrixMultiply(short[] aWord, short[][] table) {
    short[] result = new short[4];
    for (int i = 0; i < 4; i++) {
        result[i] = wordMultiply(table[i], aWord);
    }
    return result;
}

/**
 * 两个字在有限域GF(2)上的乘法操作
 * multiplication between two words
 * @param firstWord first operand
 * @param secondWord second operand
 * @return multiplication result, a byte actually
 */
private short wordMultiply(short[] firstWord, short[] secondWord) {
    short result = 0;
    for (int i=0; i < 4; i++) {
        result ^= multiply(firstWord[i], secondWord[i]);
    }
    return result;
}

/**
 * 有限域GF(2)上的乘法操作，通过分解操作数将之转化成有限域GF(2)上的倍乘操作
 * multiplication in finite field GF(2^8)
 * @param a an operand of this kind of multiplication
 * @param b another operand of this kind of multiplication
 * @return multiplication result
 */
private short multiply(short a, short b) {
    short temp = 0;
    while (b != 0) {
        if ((b & 0x01) == 1) {
            temp ^= a;
        }
        a <<= 1;
        if ((a & 0x100) > 0) {
            /*
             judge if a is greater than 0x80, if then subtract a
             irreducible polynomial which can be substituted by 0x1b
             cause addition and subtraction are equivalent in this case
             it's okay to xor 0x1b
             */
            a ^= 0x1b;
        }
        b >>= 1;
    }
    return (short) (temp & 0xff);
} 

6. 对外加密接口

• 将字符串形式的明文和密钥分别转换为 Nb 个字长的状态和 Nk 个字长的主密钥数组
• 通过主密钥数组生成轮密钥数组
• 将二维轮密钥数组转换成三维数组方便以 Nk 个字长为单位获取轮密钥
• 调用 coreEncrypt 方法，指定S盒运算表，列混合中用到的 CX 运算表和行变换每个字节的移位规则表
• 将最后获取到密文状态用 Base64 编码

public String encrypt(String plaintext, String key) {
    // transfer plaintext and key from one-dimension matrix
    // to (data.length / 4) x 4 matrix
    short[][] initialPTState = transfer(transferToShorts(plaintext));
    short[][] initialKeyState = transfer(transferToShorts(key));

    // obtain raw round keys
    short[][] rawRoundKeys = generateRoundKeys(initialKeyState);

    // make it easier to obtain a whole block of round key in a round transformation
    short[][][] roundKeys = transfer(rawRoundKeys);
    
    short[][] finalState = coreEncrypt(initialPTState, roundKeys, AESConstants.SUBSTITUTE_BOX,
                                       AESConstants.CX, AESConstants.SHIFTING_TABLE);
    return Base64Util.encode(transfer2Bytes(finalState));
} 

7. 核心加密逻辑

/**
 * AES核心操作，通过将可逆操作抽取成可逆矩阵作为参数，使该方法能在加/解密操作中复用
 * @param initialPTState    明文或密文的状态数组
 * @param roundKeys     加/解密要用到的轮密钥数组
 * @param substituteTable   加/解密要用到的S盒
 * @param mixColumnTable    列混合中用来取代既约多项式的数组
 * @param shiftingTable    行变换中用来决定字间左移的位数的数组
 * @return 加/解密结果
 */
private short[][] coreEncrypt(short[][] initialPTState,
                              short[][][] roundKeys, short[][] substituteTable,
                              short[][] mixColumnTable, short[][] shiftingTable) {

    // 初始轮密钥加，异或操作
    short[][] state = xor(roundKeys[0], initialPTState);

    // 处理前九轮变换
    for (int i = 0; i < 9; i++) {
        // 将状态数组的字节替换为S盒中相应位置的字节
        state = substituteState(state, substituteTable);
        // 行移位变换
        state = shiftRows(state, shiftingTable);
        // 列混合变换
        state = mixColumns(state, mixColumnTable);
        // 轮密钥加变换
        state = xor(roundKeys[i + 1], state);
    }

    // 处理最后一轮
    state = substituteState(state, substituteTable);
    state = shiftRows(state, shiftingTable);
    state = xor(roundKeys[roundKeys.length - 1], state);
    return state;
} 

四. 解密过程

说到加密先纵观整个 AES 的加解密流程，由于 Rijndael 算法不是对合运算，所以其解密算法与加密算法不同，根据解密算法应当是加密算法的逆，最直接的做法就是把加密算法倒序执行，便得到解密算法，但是这样不便于工程实现。

由于 Rijndael 算法的巧妙设计，使得我们只需稍微改变密钥扩展策略，同时把加密算法的基本运变换成逆变换，便得到解密算法，其算法结构其实与加密算法的结构相同。

1. AES基本逆变换

1.1. AddRoundKey

轮密钥加变换的逆就是其本身，即

1.2. ShiftRows

行移位变换的逆是状态的后三行分别移位Nb - C1， Nb - C2， Nb - C3个字节。

1.3. MixColumns

因为列混合变换是把状态的每一列都乘以一个固定的多项式 c(x) :

所以列混合变换的逆就是状态的每列都乘以 c(x) 的逆多项式 d(x)：

1.4. SubBytes

S 盒变换的逆要先进行逆仿射变换，再把每个字节用其在 GF(28) 中的逆来代替。

1.5. KeyExpansion

解密的密钥扩展与加密的密钥扩展不同，其定义如下：

• 使用加密算法的密钥扩展
• 把 InvMixColumn 应用到除第一和最后一轮外的所有轮密钥上

另外得到的逆轮密钥数组在轮变换中需要倒序使用，即 Round1 使用 roundKey(Nr+1)

2. 对外的解密接口

• 使用 Base64 编码将密文解码并得到初始状态，获取密钥数组
• 调用私有的核心解密函数得到解密后的明文状态
• 将明文状态还原为字符串（不考虑中文编码）

public String decrypt(String encryptedText, String key) {
    short[][] initialTextState = transfer(Base64Util.decodeToShorts(encryptedText));
    short[][] initialKeyState = transfer(transferToShorts(key));

    short[][] decryptState = coreDecrypt(initialTextState, initialKeyState);
    return getOrigin(decryptState);
} 

3. 核心解密逻辑

获取加密轮密钥逆变换数组，复用核心加密函数即可，主要差别在于逆变换，大体步骤如下

• 使用加密算法的密钥扩展得到轮密钥数组，并对之进行维数处理
• 对中间 Nr-1 个密钥进行逆列混合变换
• 为了便于操作将上述步骤得到的解密轮密钥数组逆转，这样便可通过改变参数复用加密算法的结构

/**
 * 解密逻辑：通过将可逆操作抽取成可逆矩阵, 复用加密核心函数
 * @param encryptedTextState initial encrypted text state
 * @param keyState initial key state
 * @return decrypted state
 */
private short[][] coreDecrypt(short[][] encryptedTextState, short[][] keyState) {
    // obtain raw round keys
    short[][] rawRoundKeys = generateRoundKeys(keyState);

    // make it easier to obtain a whole block of round key in a round transformation
    short[][][] roundKeys = transfer(rawRoundKeys);

    // 对中间9个密钥进行逆列混合变换
    for (int i = 1; i < roundKeys.length - 1; i++) {
        roundKeys[i] = mixColumns(roundKeys[i], AESConstants.INVERSE_CX);
    }

    short[][][] inverseRoundKeys = inverseRoundKeys(roundKeys);
    return coreEncrypt(encryptedTextState, inverseRoundKeys, AESConstants.
                       INVERSE_SUBSTITUTE_BOX, AESConstants.INVERSE_CX, AESConstants.INVERSE_SHIFTING_TABLE);
}

/**
 * [解密] 将解密扩展密钥数组逆转，方便复用核心加密操作，
 * @param roundKeys 解密扩展密钥数组
 * @return 逆转了的解密扩展密钥数组
 */
private short[][][] inverseRoundKeys(short[][][] roundKeys) {
    short[][][] result = new short[roundKeys.length][4][4];
    int length = roundKeys.length;
    for (int i = 0; i < roundKeys.length; i++) {
        result[i] = roundKeys[length - 1 - i];
    }
    return result;
} 

五. 测试

@Test
public void testAES() throws UnsupportedEncodingException {
    String plaintext = "passwordTextCase", key = "simpleKeyCase123";
    CipherService aesService = new AESCipherService();
    String encryptedText = aesService.encrypt(plaintext, key);

    ArrayUtil.printInfo("encrypted text", encryptedText, false);
    aesService.decrypt(encryptedText, key);
} 

1. 加密结果

#####################  encryption  #####################
plaintext text                passwordTextCase              
key text                      simpleKeyCase123              
initial plaintext state       70617373776f72645465787443617365
initial key state             73696d706c654b657943617365313233

RoundKeys
[RoundKey 1]                  73696d706c654b657943617365313233
[RoundKey 2]                  b54aae3dd92fe558a06c842bc55db618
[RoundKey 3]                  fb04039b222be6c3824762e8471ad4f0
[RoundKey 4]                  5d4c8f3b7f6769f8fd200b10ba3adfe0
[RoundKey 5]                  d5d26ecfaab5073757950c27edafd3c7
[RoundKey 6]                  bcb4a89a1601afad4194a38aac3b704d
[RoundKey 7]                  7ee54b0b68e4e4a62970472c854b3761
[RoundKey 8]                  8d7fa49ce59b403acceb071649a03077
[RoundKey 9]                  ed7b51a708e0119dc40b168b8dab26fc
[RoundKey 10]                 948ce1fa9c6cf0675867e6ecd5ccc010
[RoundKey 11]                 e9362bf9755adb9e2d3d3d72f8f1fd62

N = 1
SubBytes                      7b30727baf67127cd8f7d4c5f75383b1
ShiftRows                     7b67d4b1aff7837bd853727cf73012c5
MixColumns                    3a636747bfbfc8685094ebaa7264b7b1
RoundKey                      b54aae3dd92fe558a06c842bc55db618
AddRoundKeys                  8f29c97a66902d30f0f86f81b73901a9

N = 2
SubBytes                      73a5ddda3360d8048c41a80ca9127cd3
ShiftRows                     7360a8d333417cda8c12dd04a9a5d80c
MixColumns                    3d8336e003efffc7ecd033486987b385
RoundKey                      fb04039b222be6c3824762e8471ad4f0
AddRoundKeys                  c687357b21c419046e9751a02e9d6775

N = 3
SubBytes                      b4179621fd1cd4f29f88d1e0315e859d
ShiftRows                     b41cd19dfd8885219f5e96f23117d4e0
MixColumns                    1b79ad2bc6430753a370fb8d6f98ae4b
RoundKey                      5d4c8f3b7f6769f8fd200b10ba3adfe0
AddRoundKeys                  46352210b9246eab5e50f09dd5a271ab

N = 4
SubBytes                      5a9693ca56369f6258538c5e033aa362
ShiftRows                     5a368c625653a3ca583a936203969f5e
MixColumns                    00dbc99030c41d850fe0f98566d052b0
RoundKey                      d5d26ecfaab5073757950c27edafd3c7
AddRoundKeys                  d509a75f9a711ab25875f5a28b7f8177

N = 5
SubBytes                      03015ccfb8a3a2376a9de63a3dd20cf5
ShiftRows                     03a3e6f5b89d0ccf6ad25c373d01a23a
MixColumns                    eb9a73b1144277c7d206595ee1f82d90
RoundKey                      bcb4a89a1601afad4194a38aac3b704d
AddRoundKeys                  572edb2b0243d86a9392fad44dc35ddd

N = 6
SubBytes                      5b31b9f1771a6102dc4f2d48e32e4cc1
ShiftRows                     5b1a2dc1774f4cf1dc2eb902e3316148
MixColumns                    74d9434382cca8636a529deca76ac8fe
RoundKey                      7ee54b0b68e4e4a62970472c854b3761
AddRoundKeys                  0a3c0848ea284cc54322dac02221ff9f

N = 7
SubBytes                      67eb3052873429a61a9357ba93fd16db
ShiftRows                     673457db879316521afd30a693eb29ba
MixColumns                    1e2d8b67ffd2ceb3be0d76b4889fff03
RoundKey                      8d7fa49ce59b403acceb071649a03077
AddRoundKeys                  93522ffb1a498e8972e671a2c13fcf74

N = 8
SubBytes                      dc00150fa23b19a7408ea33a78758a92
ShiftRows                     dc3ba392a28e8a0f407515a77800193a
MixColumns                    dfc617d8532f32e7ad32edf5d36904e5
RoundKey                      ed7b51a708e0119dc40b168b8dab26fc
AddRoundKeys                  32bd467f5bcf237a6939fb7e5ec22219

N = 9
SubBytes                      237a5ad2398a26daf9120ff3582593d4
ShiftRows                     238a0fd4391293d2f9255ada587a26f3
MixColumns                    18e9d05305617b7506871dc0eb356049
RoundKey                      948ce1fa9c6cf0675867e6ecd5ccc010
AddRoundKeys                  8c6531a9990d8b125ee0fb2c3ef9a059

N = 10
SubBytes                      644dc7d3eed73dc958e10f71b299e0cb
ShiftRows                     64d70fcbeee1e0d35899c7c9b24d3d71
RoundKey                      e9362bf9755adb9e2d3d3d72f8f1fd62
AddRoundKeys                  8de124329bbb3b4d75a4fabb4abcc013
encrypted text                jeEkMpu7O011pPq7SrzAEw== 

2. 解密结果

#####################  decryption  #####################
encrypted text                jeEkMpu7O011pPq7SrzAEw==      
key text                      simpleKeyCase123              
initial encrypted state       8de124329bbb3b4d75a4fabb4abcc013
initial key state             73696d706c654b657943617365313233

RoundKeys
[RoundKey 1]                  73696d706c654b657943617365313233
[RoundKey 2]                  b54aae3dd92fe558a06c842bc55db618
[RoundKey 3]                  fb04039b222be6c3824762e8471ad4f0
[RoundKey 4]                  5d4c8f3b7f6769f8fd200b10ba3adfe0
[RoundKey 5]                  d5d26ecfaab5073757950c27edafd3c7
[RoundKey 6]                  bcb4a89a1601afad4194a38aac3b704d
[RoundKey 7]                  7ee54b0b68e4e4a62970472c854b3761
[RoundKey 8]                  8d7fa49ce59b403acceb071649a03077
[RoundKey 9]                  ed7b51a708e0119dc40b168b8dab26fc
[RoundKey 10]                 948ce1fa9c6cf0675867e6ecd5ccc010
[RoundKey 11]                 e9362bf9755adb9e2d3d3d72f8f1fd62

inverse roundKeys
[RoundKey 1]                  e9362bf9755adb9e2d3d3d72f8f1fd62
[RoundKey 2]                  708e03febe111cd46ee2ba036852f407
[RoundKey 3]                  513f2d23ce9f1f2ad0f3a6d706b04e04
[RoundKey 4]                  16b3b0df9fa032091e6cb9fdd643e8d3
[RoundKey 5]                  de6e462d891382d681cc8bf4c82f512e
[RoundKey 6]                  0dc56d9f577dc4fb08df092249e3dada
[RoundKey 7]                  e0240c6e5ab8a9645fa2cdd9413cd3f8
[RoundKey 8]                  e0ec63caba9ca50a051a64bd1e9e1e21
[RoundKey 9]                  a13297635a70c6c0bf86c1b71b847a9c
[RoundKey 10]                 1d7fded0fb4251a3e5f60777a402bb2b
[RoundKey 11]                 73696d706c654b657943617365313233

N = 1
SubBytes                      8c0dfb5999e0a0a95ef931123e658b2c
ShiftRows                     8c6531a9990d8b125ee0fb2c3ef9a059
MixColumns                    53040c2a87038f0697c7e0d93028d2f4
RoundKey                      708e03febe111cd46ee2ba036852f407
AddRoundKeys                  238a0fd4391293d2f9255ada587a26f3

N = 2
SubBytes                      32cffb195b39227f69c2467a5ebd237e
ShiftRows                     32bd467f5bcf237a6939fb7e5ec22219
MixColumns                    8d048eb16c1195259086b3707eb0573e
RoundKey                      513f2d23ce9f1f2ad0f3a6d706b04e04
AddRoundKeys                  dc3ba392a28e8a0f407515a77800193a

N = 3
SubBytes                      934971741ae6cffb723f2f89c1528ea2
ShiftRows                     93522ffb1a498e8972e671a2c13fcf74
MixColumns                    7187e7041833245b0491895b45a8c169
RoundKey                      16b3b0df9fa032091e6cb9fdd643e8d3
AddRoundKeys                  673457db879316521afd30a693eb29ba

N = 4
SubBytes                      0a28da9fea22ff48432108c5223c4cc0
ShiftRows                     0a3c0848ea284cc54322dac02221ff9f
MixColumns                    85746becfe5cce275de232f62b1e3066
RoundKey                      de6e462d891382d681cc8bf4c82f512e
AddRoundKeys                  5b1a2dc1774f4cf1dc2eb902e3316148

N = 5
SubBytes                      5743fadd02925d2b93c3db6a4d2ed8d4
ShiftRows                     572edb2b0243d86a9392fad44dc35ddd
MixColumns                    0e668b6aefe0c834620d551574e278e0
RoundKey                      0dc56d9f577dc4fb08df092249e3dada
AddRoundKeys                  03a3e6f5b89d0ccf6ad25c373d01a23a

N = 6
SubBytes                      d571f5779a75815f587fa7b28b091aa2
ShiftRows                     d509a75f9a711ab25875f5a28b7f8177
MixColumns                    ba12800c0ceb0aae07985ebb42aa4ca6
RoundKey                      e0240c6e5ab8a9645fa2cdd9413cd3f8
AddRoundKeys                  5a368c625653a3ca583a936203969f5e

N = 7
SubBytes                      4624f0abb95071105ea222abd5356e9d
ShiftRows                     46352210b9246eab5e50f09dd5a271ab
MixColumns                    54f0b2574714202b9a44f24f2f89cac1
RoundKey                      e0ec63caba9ca50a051a64bd1e9e1e21
AddRoundKeys                  b41cd19dfd8885219f5e96f23117d4e0

N = 8
SubBytes                      c6c451752197677b6e9d35042e8719a0
ShiftRows                     c687357b21c419046e9751a02e9d6775
MixColumns                    d2523fb06931ba1a33941cb3b221a290
RoundKey                      a13297635a70c6c0bf86c1b71b847a9c
AddRoundKeys                  7360a8d333417cda8c12dd04a9a5d80c

N = 9
SubBytes                      8f906fa966f8017af039c930b7292d81
ShiftRows                     8f29c97a66902d30f0f86f81b73901a9
MixColumns                    66180a6154b5d2d83da5750b5332a9ee
RoundKey                      1d7fded0fb4251a3e5f60777a402bb2b
AddRoundKeys                  7b67d4b1aff7837bd853727cf73012c5

N = 10
SubBytes                      030a19561b2641032d501e0126083907
ShiftRows                     03081e031b0a39012d26190726504156
RoundKey                      73696d706c654b657943617365313233
AddRoundKeys                  70617373776f72645465787443617365
plaintext                     passwordTextCase 

六. 总结

本文主要讲述了 AES 的由来、数学原理、加解密过程，并提供了示例代码片段，由于这篇文章其实我在 2018 年 10 月时写的（可见我的 博客原文），其中很多数学相关的原理细节至今也忘记德差不多了，由于换了系统，原博客的 markdown 文件都已经丢失，应该不会再维护，以后有机会应该都在这里写，所以就挖过来在这里记录一下，希望对正在学习密码学的朋友有帮助。

另外，文中的代码都已经上传到 Github，有兴趣的朋友可以去看看，如果喜欢的话，希望能点个 star 或 fork 支持一下。

接下来我将给各位同学划分一张学习计划表！

学习计划

那么问题又来了，作为萌新小白，我应该先学什么，再学什么？
既然你都问的这么直白了，我就告诉你，零基础应该从什么开始学起：

阶段一：初级网络安全工程师

接下来我将给大家安排一个为期1个月的网络安全初级计划，当你学完后，你基本可以从事一份网络安全相关的工作，比如渗透测试、Web渗透、安全服务、安全分析等岗位；其中，如果你等保模块学的好，还可以从事等保工程师。

综合薪资区间6k~15k

1、网络安全理论知识（2天）
①了解行业相关背景，前景，确定发展方向。
②学习网络安全相关法律法规。
③网络安全运营的概念。
④等保简介、等保规定、流程和规范。（非常重要）

2、渗透测试基础（1周）
①渗透测试的流程、分类、标准
②信息收集技术：主动/被动信息搜集、Nmap工具、Google Hacking
③漏洞扫描、漏洞利用、原理，利用方法、工具（MSF）、绕过IDS和反病毒侦察
④主机攻防演练：MS17-010、MS08-067、MS10-046、MS12-20等

3、操作系统基础（1周）
①Windows系统常见功能和命令
②Kali Linux系统常见功能和命令
③操作系统安全（系统入侵排查/系统加固基础）

4、计算机网络基础（1周）
①计算机网络基础、协议和架构
②网络通信原理、OSI模型、数据转发流程
③常见协议解析（HTTP、TCP/IP、ARP等）
④网络攻击技术与网络安全防御技术
⑤Web漏洞原理与防御：主动/被动攻击、DDOS攻击、CVE漏洞复现

5、数据库基础操作（2天）
①数据库基础
②SQL语言基础
③数据库安全加固

6、Web渗透（1周）
①HTML、CSS和JavaScript简介
②OWASP Top10
③Web漏洞扫描工具
④Web渗透工具：Nmap、BurpSuite、SQLMap、其他（菜刀、漏扫等）

那么，到此为止，已经耗时1个月左右。你已经成功成为了一名“脚本小子”。那么你还想接着往下探索吗？

阶段二：中级or高级网络安全工程师（看自己能力）

综合薪资区间15k~30k

7、脚本编程学习（4周）
在网络安全领域。是否具备编程能力是“脚本小子”和真正网络安全工程师的本质区别。在实际的渗透测试过程中，面对复杂多变的网络环境，当常用工具不能满足实际需求的时候，往往需要对现有工具进行扩展，或者编写符合我们要求的工具、自动化脚本，这个时候就需要具备一定的编程能力。在分秒必争的CTF竞赛中，想要高效地使用自制的脚本工具来实现各种目的，更是需要拥有编程能力。

零基础入门的同学，我建议选择脚本语言Python/PHP/Go/Java中的一种，对常用库进行编程学习
搭建开发环境和选择IDE，PHP环境推荐Wamp和XAMPP，IDE强烈推荐Sublime；

Python编程学习，学习内容包含：语法、正则、文件、 网络、多线程等常用库，推荐《Python核心编程》，没必要看完

用Python编写漏洞的exp,然后写一个简单的网络爬虫

PHP基本语法学习并书写一个简单的博客系统

熟悉MVC架构，并试着学习一个PHP框架或者Python框架 (可选)

了解Bootstrap的布局或者CSS。

阶段三：顶级网络安全工程师

如果你对网络安全入门感兴趣，那么你需要的话可以点击这里👉网络安全重磅福利：入门&进阶全套282G学习资源包免费分享！

学习资料分享

当然，只给予计划不给予学习资料的行为无异于耍流氓，这里给大家整理了一份【282G】的网络安全工程师从入门到精通的学习资料包，可点击下方二维码链接领取哦。

探索吗？**

阶段二：中级or高级网络安全工程师（看自己能力）

综合薪资区间15k~30k

7、脚本编程学习（4周）
在网络安全领域。是否具备编程能力是“脚本小子”和真正网络安全工程师的本质区别。在实际的渗透测试过程中，面对复杂多变的网络环境，当常用工具不能满足实际需求的时候，往往需要对现有工具进行扩展，或者编写符合我们要求的工具、自动化脚本，这个时候就需要具备一定的编程能力。在分秒必争的CTF竞赛中，想要高效地使用自制的脚本工具来实现各种目的，更是需要拥有编程能力。

零基础入门的同学，我建议选择脚本语言Python/PHP/Go/Java中的一种，对常用库进行编程学习
搭建开发环境和选择IDE，PHP环境推荐Wamp和XAMPP，IDE强烈推荐Sublime；

Python编程学习，学习内容包含：语法、正则、文件、 网络、多线程等常用库，推荐《Python核心编程》，没必要看完

用Python编写漏洞的exp,然后写一个简单的网络爬虫

PHP基本语法学习并书写一个简单的博客系统

熟悉MVC架构，并试着学习一个PHP框架或者Python框架 (可选)

了解Bootstrap的布局或者CSS。

阶段三：顶级网络安全工程师

如果你对网络安全入门感兴趣，那么你需要的话可以点击这里👉网络安全重磅福利：入门&进阶全套282G学习资源包免费分享！

学习资料分享

当然，只给予计划不给予学习资料的行为无异于耍流氓，这里给大家整理了一份【282G】的网络安全工程师从入门到精通的学习资料包，可点击下方二维码链接领取哦。