MindSpore AI科学计算系列 | 几何深度学习系列——统一视角下的神经网络

背景

在上一篇科学计算系列文章中，我们简单介绍了对称性与群的概念，以及对称性如何在几何学与物理学中如何扮演第一原理的角色。在本篇文章我们将看到，几何深度学习可以视为深度学习领域的埃尔朗根纲领，以对称性为第一原理，统一和分类各种神经网络架构。

1、对称性与神经网络

随着算力的快速提升，深度学习发展迅速，并在计算视觉、自然语言等诸多领域展现其独有的优势。现如今，从最初的多层感知神经网络(MLP)，到现在各类诸如卷积神经网络(CNN)、循环神经网络(RNN)、图神经网络(GNN)以及Transformer等不同的神经网络架构，我们处于与十九世纪末几何学类似的情形。近几年，研究者以对称性为第一原理，发展出一套统一的神经网络理论框架——几何深度学习。其中，研究者提出“5G”概念，即五个在几何深度学习中重要的研究对象：Grids（格网）、Group（群）、Graphs（图）、Geodesics（测地线）、Gauges（规范）。

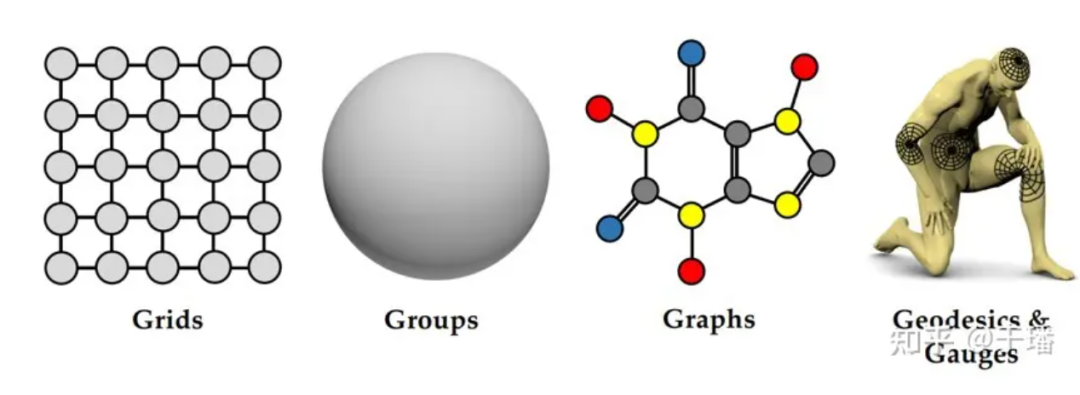
图1："5G"

2、空间与特征场

为了对神经网络有更进一步的理解，我们需要明确两个概念：空间和特征场。简单的说，空间是指信息在空间尺度上的延展，特征场则在空间上的每一点定义了一个特征矢量，神经网络的本质是一个特征场之间的映射。

我们不妨回顾一下前面几类神经网络架构：MLP没有空间尺度，换句话说空间为一个点，而特征场即为网络层中的特征，MLP将一层中的特征映射到下一层的特征；二维CNN空间尺度为二维离散平面，特征场为平面上每一点的通道信息，包括最初的RGB通道，以及隐藏层中的多个通道信息。类似地，RNN是在时序尺度上延展，GNN是在一般的图结构上延展，而Transformer可以视为一个特殊的完全图GNN。

群的表示指群到线性空间的同态映射。空间中点的变换通过对称变换群描述，与之对应的特征场之间的变换通过对称变换群的表示描述。换句话说，神经网络映射是表示之间的映射。

以图片为例，图片上一个点的特征为RGB三个数值，即三个标量的直和，如图5上所示。这里的标量就是变换群的平凡表示，其数值在变换群的作用下保持不变。平凡表示是指，对于任意变换群，表示映射都将其映射为一个恒等矩阵，这意味着对称性信息在映射过程中损失了。如果要求神经网络保持一定的对称性，那么需要我们用非平凡表示来描述特征场的变换，其表示矩阵的直和分解会存在维度大于1的子矩阵，于是神经网络则为每一块子矩阵保持对称性的映射，如图2下所示。

图2：特征场间变换群的表示

3、不变性与等变性

正如我们上面提到的，如果特征场的变换只是一些平凡表示，那么神经网络作为一个特征场之间的映射，对输入特征场的变换不会影响其输出特征场，则称神经网络对此变换群具有不变性。

而对于非平凡表示，对输入特征场的变换，会导致其输出特征场做相应的变换，变换方式取决于变换群的表示，则称神经网络对此变换群具有等变性。可以看到，映射的不变性是等变性的一种特例。

直观的理解，神经网络的等变性保持了某种对称性信息。例如，CNN具有空间平移等变性，图像识别任务中，当图像中一个物体进行平移时，其特征图像也会进行相应的平移，因此网络可以正确地识别这个物体；类似地，RNN具有时序平移等变性，只是这里的平移是有方向性的；GNN具有顶点编号的规范等变性，如果用邻接矩阵表示图的信息，那么对图顶点编号的置换变换，也会同样反应到邻接矩阵上。而对于最基础的MLP，其具有数据集合置换规范等变性。

可以看到，任何神经网络都是某种对称性的等变映射。在[2]中，作者提出了另一个关于等变性的重要结论：等变性 = 坐标无关 + 权值共享。例如CNN的等变性可以看作空间位置坐标无关，结合卷积核在空间平移中权值共享。特征场这个观察加深了人们对于等变性的理解，对于在更一般的空间结构，例如弯曲空间中设计神经网络非常重要。我们会在后面简单介绍一下如何在黎曼流形上进行卷积。

4、范畴论观点

我们还可以进一步抽象，从范畴论的角度来看神经网络的本质。

范畴是数学的一种抽象工具，用来描述不同的数学结构及它们之间的关系。一个范畴由以下三个部分组成：

1、一类对象，可以是集合、群、拓扑空间等任何具有某种结构的数学实体。

2、一类态射，可以是函数、群同态、连续映射等任何保持结构的映射。每个态射都有一个源对象和一个目标对象，表示映射的方向。

3、一种态射的复合运算，满足结合律和单位元的存在性。

一个范畴的例子是集合范畴，它的对象是所有的集合，它的态射是所有的函数，它的复合运算就是函数的复合。

函子是范畴间的一类映射，可以将一个范畴的对象和态射变换到另一个范畴中，同时保持单位态射和态射的复合。例如，群的表示是一种函子，它将群范畴映射到线性空间范畴。

自然变换是一种将一个函子变为另一个函子的映射，同时保持范畴的内在结构不变。

前面提到，所有的神经网络都是某种对称性的等变映射，如果我们从范畴论的视角来看，这个结论是显然的，因为神经网络的本质是群表示函子的自然变换，不同范畴对应于不同的网络架构。例如集合范畴对应于MLP，而图范畴对应于GNN。

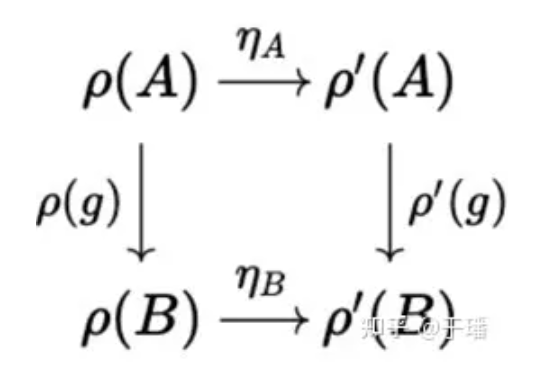
图3：群表示函子ρ(g)的自然变换η

5、神经网络设计蓝图

至此，我们对神经网络有了一个统一的整体理解，由此可以获得一般性的神经网络设计蓝图：

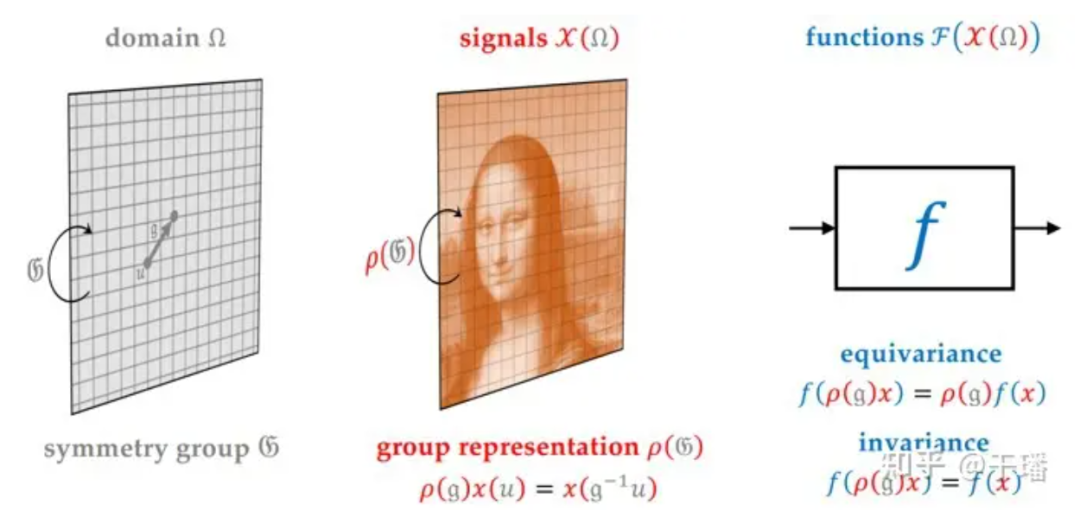
图4：神经网络设计蓝图

一个神经网络需要明确信息延展的空间/域(domain)，空间的变换群(G)，空间上的特征场/信号(signals)，特征场的变换的表示(ρ(G))。网络包含以下几个模块：线性等变层，非线性（等变）层，局部池化层（粗粒化），线性不变层（全局池化）。

以CNN为例，空间是二维离散平面，变换群是二维平移群，特征场是图片的通道信息，变换的表示是平凡表示，线性等变层是卷积层，非线性层可以是任意非线性函数（因为特征场由标量组成，不会对非线性层做出约束），局部池化层是CNN中的池化层，线性不变层是网络末端的MLP。

图5：CNN网络架构

至此，我们从宏观统一的视角回顾了各类神经网络架构，并介绍了具有对称性的神经网络设计蓝图。在下一篇文章中，我们将具体来看看三类典型具有对称性的神经网络：图神经网络、群等变神经网络和流形上的神经网络。

参考文献

[1]Bronstein, Michael M., et al. "Geometric deep learning: Grids, groups, graphs, geodesics, and gauges." arXiv preprint arXiv:2104.13478 (2021).

[2]Weiler, Maurice, et al. "Coordinate Independent Convolutional Networks--Isometry and Gauge Equivariant Convolutions on Riemannian Manifolds." arXiv preprint arXiv:2106.06020 (2021).