形式语言与自动机 下推自动机

下推自动机是啥？：

下面是他的模型：

如何运转？：

 下面是标准定义，属实有点复杂：

注意状态转移函数成分极其复杂，要考虑现有状态，要考虑输入符号，还要考虑栈。

一些约定：

大写的是栈里的，小写的是输入带上的。

例子： 

 

例子：

这里有一个问题：输入0001111怎么办？：

确实进入q2了，毕竟只要栈空了就会进去，但是还要输入一个1，当前处于的状态q1,q2都没有定义在栈空了的情况输入1会发生什么，直接进入deadState.

例子：

 

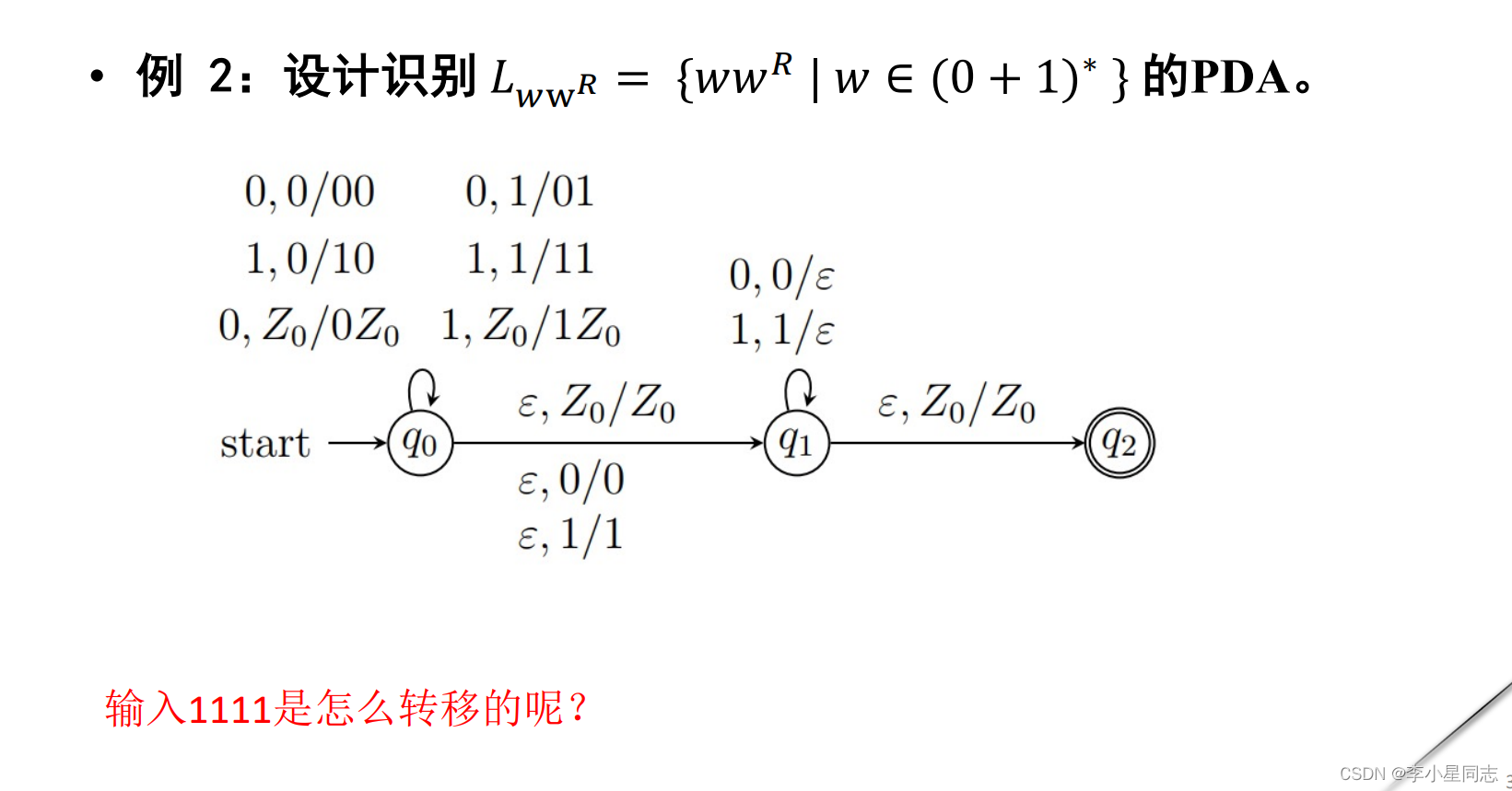
下推自动机接受那些语言？：

终态接受就是在一个状态上接受，不管栈的情况。（虽然进入这个状态本身可能需要栈是空的）以空栈接受就是状态是普通的状态，只有在空栈的时候才会接受。

 注意：Y是单个字符不是整个字符串。加上X0是因为中途栈可能会出现Z0也没了的情况（这在状态终点的PDA中是可能的），这样会直接进入终态，所以不行，要再加一个保险，反正X0是绝对不可能在Pf阶段没得（那原本的那个终态接受就不成立），只有在最后不分青红皂白全部弹出的时候才会没。

 

 

这个好理解多了：X0冒头了直接转到Pf。这个X0只是指示作用，好像拿走了也不会误会。

这里解释一下：为什么这些图里面都是看到空栈就跟见了鬼一样直接跑到接收状态去？不怕字符串还没输入完吗？不怕，因为继续输入原本的接收状态也会没。

下推自动机和上下文无关文法的等价性。

看不太懂？来看例子：

 可以发现，一上来还没有开始读字符串，看到栈开头有一个S,这个PDA就开始自动工作，把S的所有可能性（顺带其衍生物的可能性）都考虑了。表面上看一片正常，但这个小小的PDA里面已经蕴藏了S的全部可能，也就是这个上下文无关文法的全部可能，只要输入的字符串符合其中一个，某一个栈就会空，然后就成了。

这个原理的构造方法我们已经知道了。证明我们就省略了，反正之前已经讲过了。

当然也有另一种方法：

例子：

 那怎么通过PDA构造CFG呢？：

我们可以从第一步开始看：Q0Z0p是q0到p中途还要弹出z0所使用的字符串。这个字符串假如输入PDA肯定是能过的，同时我们把它构造成了S派生的字符串，也就是说这一部分是没有问题的。

阀(1,a,X)是一个集合，因为PDA是不定的嘛，可以有多个下个状态，所以有了一个集合。而设某一个下个状态是（p,Y1Y2……），那qXrn，也就是从q到rn首先要输入a，状态变成p,栈里的字符串变成了Y1Y2……，然后就是显而易见。

Y1Y2……四大皆空了更好，那显然qXp想要弹出X并进入p只要一个a就可以了。 

有点复杂，先看例子：（没写接收状态就是空栈接受）
 首先是看S可以直接派生的。显然这两个具体是什么我们不能直接看出来。

那我们就用之前的公式寻找突破口。要求q0Z0q0,可以先到q0再到q0，也可以先到q1再到q0.这样我们就有了两个表达式。加起来有四个。

第一级问题解决了，但出现了q0Xq0,q0Xq1,q1Xq0,q1Xq1四个未知的东西，怎么说？

这个时候已经没有从未出现过的变量了，这个体系可以自圆其说（肯定不是最简的）。

 消除无用符号：

确定形下推自动机：

这个没有空的转移，没有多条线路。有点奇怪的是能力和PDA不一样。

 

没有了栈不就是DFA吗，但DPDA有栈的话显然还可以有更多选择，因此DPDA还要更大一些。

 

N(P)就是把P的一部分满足前缀性质的拿出来。

 

语言之间的关系：

 

CFL>DCFL>Regular(CFL是上下文无关语言，也就是下推自动机的语言，regular是正则)