05.线性回归介绍

最新推荐文章于 2022-09-28 08:00:01 发布

LWY_Xing

最新推荐文章于 2022-09-28 08:00:01 发布

阅读量899

点赞数

分类专栏：自然语言处理文章标签：机器学习人工智能 python 自然语言处理

本文链接：https://blog.csdn.net/LWY_Xing/article/details/110928565

版权

自然语言处理专栏收录该内容

9 篇文章 0 订阅

订阅专栏

【数学基础】

什么是线性回归？
线性：两个变量之间的关系是一次函数（图像是直线）；
非线性：两个变量之间的关系是非一次函数（图像不是直线）；
回归：人们在测量事物的时候因为客观条件的限制，求的都是测量值，而不是事物的真实值，为了能够得到真实值无限次测量，最后通过这些测量数据计算回归到真实值，这就是回归的由来；
一般表达式： $y = w x + b$
均方误差（MSE）：欧氏距离（损失函数）
$J=\frac{1}{2m}\displaystyle\sum_{i=1}^m(y'-y)^2$
最小化损失函数优化方法：
【最小二乘法】
二乘的含义：损失函数中的平方
最小二乘：最小均方差
步骤：
1）直接对损失函数求参数的偏导；
2）令导数为0，导数为0的时候二次函数取得最小值；
$y = w x + b$
$L=\displaystyle\sum(y'-y)^2$
$\frac{\partial L}{\partial w}=2\displaystyle\sum(y'_i-y_i)x_i=2\displaystyle\sum(wx_i+b-y_i)x_i=0$
$\frac{\partial L}{\partial b}=2\displaystyle\sum(y'_i-y_i)=2\displaystyle\sum(wx_i+b-y_i)=0$
【梯度下降法】
目标：寻找某个凸函数的最小值
凸函数：某段区间只有一个低谷的函数
含义：朝着导数变小的方向逐步更新参数
梯度：导数的方向
步骤：
1）随机取出一个值 $x_0$ ；
2）算出对应的 $f(x_0)$ ；
3）计算 $f(x_0)$ 处损失函数 $f (x)$ 的导数；
4）从 $f(x_0)$ 处开始，沿着该处导数的方向增加 $\alpha$ ，此时取值为 $x_1$ ，那么 $\frac{|x_1-x_0|}{\alpha}$ 的值为 $f (x)$ 在 $f(x_0)$ 的斜率；
5）重复2~4步骤，直到达到退出的条件（比如设定循环N次后停止）；
$w\leftarrow{w-\alpha*\frac{\partial L}{\partial w}}$
$b\leftarrow{b-\alpha*\frac{\partial L}{\partial b}}$

【梯度下降实战案例】

import numpy as np

m = 20
X0 = np.ones((m, 1))
X1 = np.arange(1, m+1).reshape(m, 1)
X = np.hstack((X0, X1))
y = np.array([3,4,5,5,2,4,7,8,11,8,12,11,13,13,16,17,18,17,19,21]).reshape(m, 1)
alpha = 0.01
#print(X)
#print(y)

def error_function(X, y, w):
    diff = np.dot(X, w) - y
    return (1./2*m) * np.dot(np.transpose(diff), diff)

def gradient_function(X, y, w):
    diff = np.dot(X, w) - y
    return (1./m) * np.dot(np.transpose(X), diff)

def gradient_decent(X, y, alpha):
    w = np.array([1, 1]).reshape(2, 1)
    gradient = gradient_function(X, y, w)
    while not np.all(np.absolute(gradient) <= 1e-5):
        w = w - alpha * gradient
        gradient = gradient_function(X, y, w)
        error = error_function(X, y, w)
        print('gradient = ', gradient)
        print('update w parm = ', w)
        print('new error = ', error[0][0])
    return w

w = gradient_decent(X, y, alpha)
print('w = ', w)
print('error function = ', error_function(X, y, w)[0][0])

…
gradient = [[ 1.00219817e-05]
[-7.34495380e-07]]
update w parm = [[0.51583296]
[0.96992163]]
new error = 405.9849624936439
gradient = [[ 9.99888389e-06]
[-7.32802599e-07]]
update w parm = [[0.51583286]
[0.96992163]]
new error = 405.98496249324046
w = [[0.51583286]
[0.96992163]]
error function = 405.98496249324046

【过拟合/欠拟合】

根据以下图可以很形象了解过拟合和欠拟合：
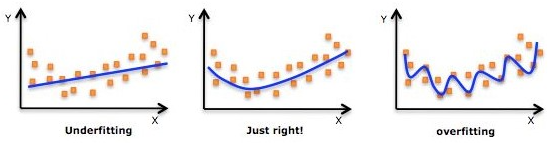
在这里插入图片描述
解决过拟合的方式有很多，其中一种就是改变损失函数，加入正则项，即给损失函数加上一个参数项，正则化项有L1/L2正则化，好处如下：

控制参数幅度，不让模型无法无天；
限制参数搜索空间；
解决过拟合与欠拟合问题；

【L1正则化（Lasso回归）】

L1正则化与L2正则化的区别在于惩罚项的不同：
$J=J_0+\lambda(|w_1|+|w_2|)$
求解 $J_0$ 的过程可以通过画出等值线，同时L1正则化函数也可以在 $w_1w_2$ 的二维平面画下来，如下：
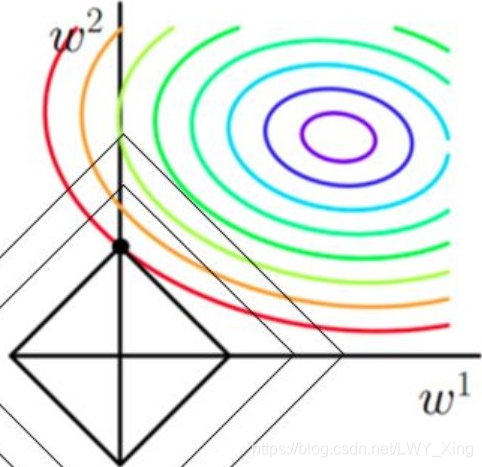
在这里插入图片描述
L1正则化结合上面的图理解：

椭圆代表 $y=w_1x_1+w_2x_2$ 线性函数的代价函数 $J=(y'-y)^2$ ；
其中椭圆上面的等值线表示确定某点 $w_1w_2$ 后， $y$ 函数的代价函数值，同一等值线上面的其他 $w_1w_2$ 的代价函数值是相等的；
L1为菱形，即为 $J=J_0+\lambda(|w_1|+|w_2|)$ 后面 $w_1|+|w_2|)$ 的图像，其中相同的等值线上 $w_1$ 和 $w_2$ 的绝对值之和是相等的；
为了使整个 $J$ 最小，保证L1最小的同时 $J_0$ 也是最小的，此时刚好 $J_0$ 椭圆会与L1菱形相切的地方在坐标轴上，所以此时肯定会有 $w_1$ 或者 $w_2$ 为0，说明L1正则化很容易就得到稀疏解（解向量中0比较多）；
什么情况下使用L1正则化？L1正则化可以使得一些特征的系数变小，甚至还可以使一些绝对值较小的系数值直接变为0，从而强化模型的泛化能力。对于高的特征数据，尤其是线性关系是稀疏的，就采用L1正则化。或者要想在一堆特征里面找出主要的特征，那么L1正则化更是首选；

【L2正则化（岭回归）】

方程表达式：
$J=J_0+\lambda\displaystyle\sum{w^2}$
假设只有两个特征，相应也只有两个 $w_1w_2$ 参数，转化：
$J=J_0+\lambda(w_1^2+w_2^2)$
为了方便表示，令：
$L=\lambda(w_1^2+w_2^2)$
与L1同理，我们的任务是在 $L$ 约束下求出 $J$ 取最小值的解，求解 $J_0$ 的过程可以画出等值线，同时L2正则化的函数 $L$ 也可以在 $w_1w_2$ 的二维平面画出来：
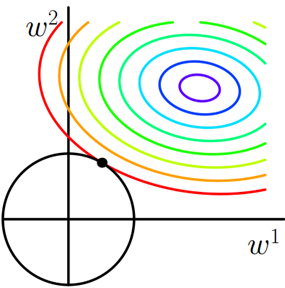
在这里插入图片描述

$L$ 表示为图中的黑色圆形，随着梯度下降法的不断逼近，与圆第一次产生交点，而这个交点很难出现在坐标轴上。这就说明了L2正则化不容易得到稀疏矩阵，同时为了求出损失函数的最小值，使得 $w_1$ 和 $w_2$ 无限接近于0，达到防止过拟合的问题。L2范数能让解比较小（靠近0），但是比较平滑（不等于0）；
什么场景下使用L2正则化？只要数据线性相关，用LinearRegression拟合的不是很好，那么就需要正则化，可以考虑使用L2正则化；如果输入的特征的维度很高，而且是稀疏线性关系，L2正则化就不太合适，需要考虑L1正则化；

【如何选择回归器？】

假如有很多维的向量特征，比如特征高达好几百，他们之间的共线性比较强（意思是不太独立，一个特征完全可以被另外一个特征替代），这种情况下强烈建议使用L1 lasso回归。为什么？因为它可以把某些模型参数置为0。共线性比较强的两个特征只会保留其中一个特征的参数值，另一个置为0。最终得到一个比较稀疏的参数向量，比密集的参数更小，计算观察都更好。
如果数据不满足以上条件，那千万不能使用L1，因为他会把有些信息压缩，即有一点共线性的特征其中不太重要的特征，但是又有一些重要信息量的特征参数给置为0了，这些参数的价值就被抛弃了。

【何为特征的共线性？】

比如预测房价问题，那么房间数量、面积（实际使用面积、公摊面积）等特征，其实实际使用面积和房间的总面积共线性是非常强的，也就是说他两的皮尔逊相关性系数非常高，对于这种特征如何判断？可以画一个相关性矩阵，求导画热分布图，颜色越深共线性就越高；
如果要求连续型随机变量之间的线性相关性，用的就是皮尔逊相关性系数，如果是离散型变量之间的线性相关性就可以使用互信息求；

【线性回归是否需要归一化？】

线性回归也是对距离度量，归一化、标准化有要求的算法；
在梯度下降过程中，房间w1(x1分布到0-5)，w2(x2分布到30-2000)，如果x1/x2不进行归一化，w1和w2这两个权重没有可比性，比如房价为5(百万)，可以看出w1x1+w2x2，其中w2的参数肯定要很小才行(0.0001)，但房间数w1是很正常的0.2，这两个w不可比就不利于最后输出w向量并且判断哪些向量特征的重要性，因为特征重要性就是w值很大的特征。此时你能说面积不重要吗？因为w2很小。
如果w1取0.2，w2取0.00003，那么等值线就会非常匾：
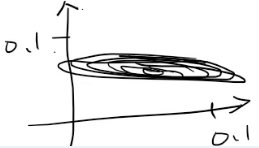
在梯度进行更新时，梯度会沿着等值线的法线一步一步走，直到椭圆心，从上图可以看出，左右等值线更新梯度变化会比较大，但是上下梯度更新会非常缓慢。法线都基本朝同一个方向，基本没啥变化。
所以线性回归是否一定要进行归一化，这个是不一定的，只是说结果不太好；
不进行归一化有两个不好的地方：
a）不利于比较特征和特征之间的重要性；
b）梯度更新比较慢；

【特征缩放：使用归一化】

z-score： $z=\frac{x-\mu}{\sigma}$
推荐使用，其中x是原始数据，u是全部数据的均值，分母为标准方差；
minmax： $x=\frac{X - X_{min}}{X_{max}-X_{min}}$
不过归一化不推荐minmax，而是z-score，为什么？
在现实生活中，一般情况下特征也好还是标签也好，只要是一个连续值，基本都符合高斯分布或者正太分布；
实际操作中：有很多利群点，极大值极大，极小值极小，原因是样本的脏数据或者自然而然产生的利群点。离群点很多，不容易清洗，这个时候 $X_{max}-X_{min}$ 差值非常大，以至于正常的分布使用这个极大值和极小值做归一，正常分布的值都会被压缩很大，精度会变低，所以不推荐使用minmax做归一化，如下离群点实例：
比如原始数据[1, 3, 6, 32, 70, 100000]，进行归一化后，[1, 3, 6, 32, 70]被压缩在0.01-0.02之间，精度变低，所以不推荐minmax归一化。不过如果你能够很容易清洗这个离群点，那么minmax归一化也是可以用的；

【离群点判断方式】

原始数据：[1, 3, 6, 10, 20, 25, 30, 32, 70, 100000]

分位数：将以上数据排序，20%分位数表示排位在前20%的数字的位置，比如3；
中位数：数在整个排位的中间；
判断：一般是把高于98%的分位点和低于20%的分位点数据当做离群点，剔除或替换为98%分位点的值本身；
画分位点工具：seaborn，可以马上知道哪些点是离群点；

【房价预测实战】

数据集地址：https://download.csdn.net/download/LWY_Xing/13665534

import pandas as pd
import numpy as np

col_names = []
with open('./readme.txt', encoding='utf8') as lines:
    for line in lines:
        column = line.split(' ')[0]
        col_names.append(column)

df = pd.read_csv('./housing_data.txt', header=None, names=col_names)
target = df['MEDV'].values
print(df.head())

from sklearn.preprocessing import MinMaxScaler
minmax_scaler = MinMaxScaler()
minmax_scaler.fit(df)
scaler_housing = minmax_scaler.transform(df)
#print(scaler_housing)
scaler_housing = pd.DataFrame(scaler_housing, columns=df.columns)
print(scaler_housing.head())

from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(scaler_housing, target)

from sklearn.metrics import mean_squared_error
pred = lr.predict(scaler_housing)
mse = mean_squared_error(pred, target)

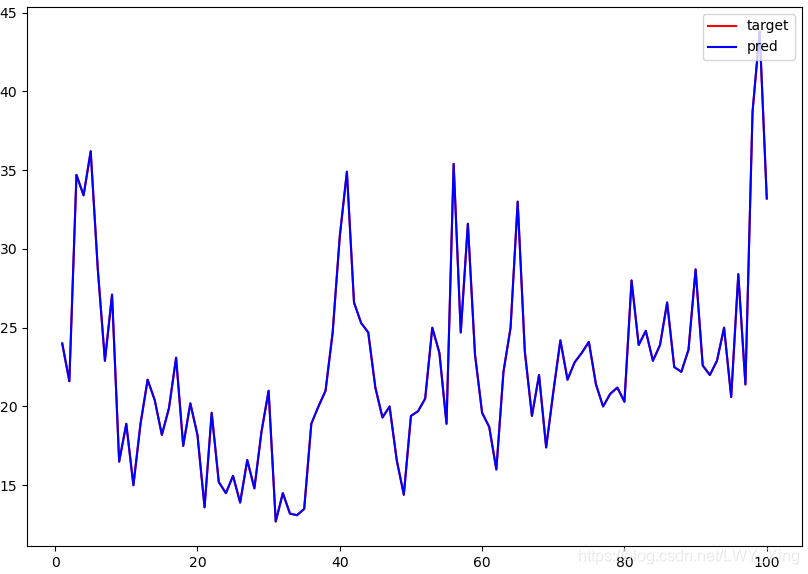
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 7))
num = 100
x = np.arange(1, num+1)
plt.plot(x, target[:num], 'r', label='target')
plt.plot(x, pred[:num], 'b', label='pred')
plt.legend(loc='upper right')
plt.show()

(base) k8s-master@k8s-master:~/Desktop/python/nlp_learning/class4$ python linear_regression.py
CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT MEDV
0 0.00632 18.0 2.31 0 0.538 6.575 65.2 4.0900 1 296.0 15.3 396.90 4.98 24.0
1 0.02731 0.0 7.07 0 0.469 6.421 78.9 4.9671 2 242.0 17.8 396.90 9.14 21.6
2 0.02729 0.0 7.07 0 0.469 7.185 61.1 4.9671 2 242.0 17.8 392.83 4.03 34.7
3 0.03237 0.0 2.18 0 0.458 6.998 45.8 6.0622 3 222.0 18.7 394.63 2.94 33.4
4 0.06905 0.0 2.18 0 0.458 7.147 54.2 6.0622 3 222.0 18.7 396.90 5.33 36.2
CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT MEDV
0 0.000000 0.18 0.067815 0.0 0.314815 0.577505 0.641607 0.269203 0.000000 0.208015 0.287234 1.000000 0.089680 0.422222
1 0.000236 0.00 0.242302 0.0 0.172840 0.547998 0.782698 0.348962 0.043478 0.104962 0.553191 1.000000 0.204470 0.368889
2 0.000236 0.00 0.242302 0.0 0.172840 0.694386 0.599382 0.348962 0.043478 0.104962 0.553191 0.989737 0.063466 0.660000
3 0.000293 0.00 0.063050 0.0 0.150206 0.658555 0.441813 0.448545 0.086957 0.066794 0.648936 0.994276 0.033389 0.631111
4 0.000705 0.00 0.063050 0.0 0.150206 0.687105 0.528321 0.448545 0.086957 0.066794 0.648936 1.000000 0.099338 0.693333

LWY_Xing

关注

0
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
05.线性回归介绍

【数学基础】什么是线性回归？线性：两个变量之间的关系是一次函数（图像是直线）；非线性：两个变量之间的关系是非一次函数（图像不是直线）；回归：人们在测量事物的时候因为客观条件的限制，求的都是测量值，而不是事物的真实值，为了能够得到真实值无限次测量，最后通过这些测量数据计算回归到真实值，这就是回归的由来；一般表达式：y=wx+by=wx+by=wx+b均方误差（MSE）：欧氏距离（损失函数）J=12m∑i=1m(y′−y)2J=\frac{1}{2m}\displaystyle\sum_{i=1
复制链接

扫一扫