稀疏矩阵操作

最新推荐文章于 2024-05-23 08:44:35 发布

铿锵的玫瑰

最新推荐文章于 2024-05-23 08:44:35 发布

阅读量5.2k

点赞数 3

分类专栏： Eigen的全面解析

本文链接：https://blog.csdn.net/LYKymy/article/details/83018978

版权

Eigen的全面解析专栏收录该内容

29 篇文章 12 订阅

订阅专栏

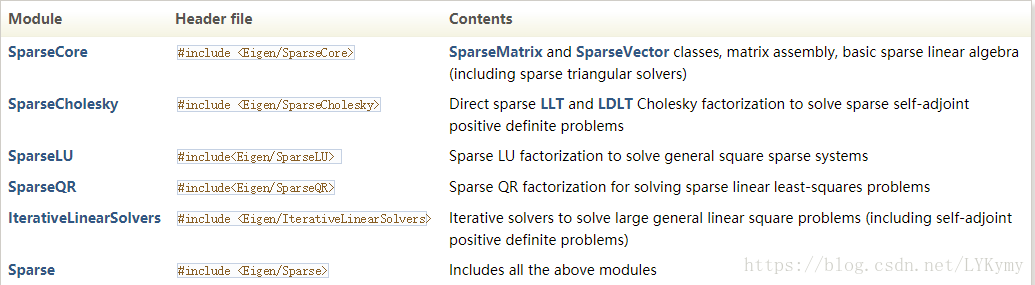
操纵和解决稀疏问题的模块

稀疏矩阵格式

在许多应用中（例如，有限元方法），通常处理非常大的矩阵，其中只有少数系数与零不同。在这种情况下，通过使用仅存储非零系数的专用表示，可以减少存储器消耗并提高性能。这种矩阵称为稀疏矩阵。

SparseMatrix类是Eigen稀疏模块的主要稀疏矩阵表示; 它提供高性能和低内存使用率。它实现了广泛使用的压缩列（或行）存储方案的更通用的变体。它由四个紧凑的数组组成：

values：存储非零的系数值。
InnerIndices：存储非零的行（resp.column）索引。
OuterStarts：为每个列（resp.row）存储前两个数组中第一个非零的索引。
InnerNNZs：存储每列的非零数（分别为行）。单词inner指的是内部向量，它是列主矩阵的列，或行主矩阵的行。 “外部”一词指的是另一个方向。

目前，保证给定内部向量的元素总是通过增加内部索引来排序。 “_”表示可用空间快速插入新元素。假设不需要重新分配，则随机元素的插入因此在O（nnz_j）中，其中nnz_j是相应内部向量的非零数。另一方面，在给定的内部向量中插入具有增加的内部索引的元素要高得多，因为这仅需要增加作为O（1）操作的相应的InnerNNZ条目。

没有空白空间的情况是特殊情况，并且被称为压缩模式。它对应于广泛使用的压缩列（或行）存储方案（CCS或CRS）。通过调用SparseMatrix :: makeCompressed（）函数，可以将任何SparseMatrix转换为此形式。在这种情况下，可以注意到InnerNNZs数组与OuterStarts是多余的，因为我们是相等的：InnerNNZs [j] = OuterStarts [j + 1] -OuterStarts [j]。因此，在实践中，对SparseMatrix :: makeCompressed（）的调用释放了此缓冲区。

值得注意的是，我们对外部库的大多数包装都需要压缩矩阵作为输入。

Eigen运算的结果总是产生压缩稀疏矩阵。另一方面，将新元素插入SparseMatrix会将其转换为未压缩模式。

第一个实例

在描述每个单独的类之前，让我们从以下典型示例开始：使用有限差分格式和Dirichlet边界条件在常规2D网格上求解拉普拉斯方程$ \ Delta u = 0 $。这个问题可以在数学上表示为$ Ax = b $形式的线性问题，其中$ x $是m个未知数的向量（在我们的例子中，是像素的值），$ b $是得到的右侧向量从边界条件来看，$ A $是一个$ m \ times m $矩阵，只包含拉普拉斯算子离散化产生的一些非零元素。

#include <Eigen/Sparse>
#include <vector>
#include <iostream>
typedef Eigen::SparseMatrix<double> SpMat; // declares a column-major sparse matrix type of double
typedef Eigen::Triplet<double> T;
void buildProblem(std::vector<T>& coefficients, Eigen::VectorXd& b, int n);
void saveAsBitmap(const Eigen::VectorXd& x, int n, const char* filename);
int main(int argc, char** argv)
{
  if(argc!=2) {
    std::cerr << "Error: expected one and only one argument.\n";
    return -1;
  }
  
  int n = 300;  // size of the image
  int m = n*n;  // number of unknows (=number of pixels)
  // Assembly:
  std::vector<T> coefficients;            // list of non-zeros coefficients
  Eigen::VectorXd b(m);                   // the right hand side-vector resulting from the constraints
  buildProblem(coefficients, b, n);
  SpMat A(m,m);
  A.setFromTriplets(coefficients.begin(), coefficients.end());
  // Solving:
  Eigen::SimplicialCholesky<SpMat> chol(A);  // performs a Cholesky factorization of A
  Eigen::VectorXd x = chol.solve(b);         // use the factorization to solve for the given right hand side
  // Export the result to a file:
  saveAsBitmap(x, n, argv[1]);
  return 0;
}

在这个例子中，我们首先定义一个双重SparseMatrix <double>的列主要稀疏矩阵类型，以及相同标量类型Triplet <double>的三元组列表。三元组是一个简单的对象，表示非零条目作为三元组：行索引，列索引，值。

在main函数中，我们声明了三元组的列表系数（作为std向量）和右侧向量$ b $，它们由buildProblem函数填充。然后将原始和非零条目的非零条目转换为真正的SparseMatrix对象A.请注意，不必对列表的元素进行排序，并且可以对可能的重复条目进行求和。

最后一步包括有效解决组装问题。由于结果矩阵A通过构造对称，我们可以通过SimplicialLDLT类执行直接Cholesky分解，该类的行为类似于密集对象的LDLT对应物。

稀疏矩阵类

SparseMatrix和SparseVector类有三个模板参数：标量类型（例如，double）存储顺序（ColMajor或RowMajor，默认为ColMajor）内部索引类型（默认为int）。

迭代非零系数

可以通过coeffRef（i，j）函数随机访问稀疏对象的元素。但是，此功能涉及非常昂贵的二进制搜索。在大多数情况下，只想迭代非零元素。这是通过外部维度上的标准循环，然后通过InnerIterator迭代当前内部向量的非零来实现的。因此，必须以与存储顺序相同的顺序访问非零条目。这是一个例子：

对于可写表达式，可以使用valueRef（）函数修改引用的值。如果稀疏矩阵或向量的类型取决于模板参数，则需要typename关键字来指示InnerIterator表示类型。

填充一个稀疏矩阵

由于SparseMatrix的特殊存储方案，在添加新的非零条目时必须特别小心。因此，在保证良好性能的同时创建稀疏矩阵的最简单方法是首先构建所谓的三元组列表，然后将其转换为SparseMatrix。

三元组的std :: vector可能包含任意顺序的元素，甚至可能包含将由setFromTriplets（）汇总的重复元素。但是，在某些情况下，通过将非零值直接插入目标矩阵，可以获得稍高的性能和更低的内存消耗。

这里的关键因素是第2行，我们为每列预留6个非零空间。在许多情况下，可以容易地预先知道每列或每行的非零数。如果每个内部向量的变化很大，那么可以通过提供一个带有operator []（int j）的向量对象来为每个内向量指定一个保留大小，返回第j个内向量的保留大小（例如，通过VectorXi或std :: vector <int>）。如果只能获得每个内向量非零值的估计值，则强烈建议高估它而不是相反。如果省略该行，则第一次插入新元素将为每个内部向量保留2个元素的空间。
第4行执行排序插入。在这个例子中，理想情况是当第j列未满并且包含其内部索引小于i的非零时。在这种情况下，此操作归结为平凡的O（1）操作。
当调用insert（i，j）时，元素i，j必须不存在，否则使用coeffRef（i，j）方法，该方法将允许例如累积值。此方法首先执行二进制搜索，如果元素尚不存在，最后调用insert（i，j）。它比insert（）更灵活，但也更昂贵。
第5行抑制剩余的空白空间并将矩阵变换为压缩列存储。