当鲁棒控制遇到强化学习：零和博弈视角的非线性拓展

       强化学习技术，包括 PPO、GRPO、SAC 和 DSAC 等主流算法，正在重塑无人机、机械臂和智能汽车的智能控制范式，但一个根本性难题始终横亘在仿真训练与现实应用之间：为什么系统不确定性总会引发控制性能的塌缩？面对外部干扰与模型误差这对耦合不确定性因素，传统鲁棒控制方法为何在干扰抑制和稳定性之间顾此失彼？这背后暗藏着一个鲁棒控制的“不可能三角”——针对非线性动力学系统，如何在不牺牲干扰抑制性能的前提下，构建抵御模型误差的钢铁防线？清华大学李升波教授课题组的最新研究，通过颠覆性的“误差对消”机制，给出了鲁棒强化学习的全新解决方案。

       诞生于上世纪 70 年代末的鲁棒控制旨在解决线性系统的不确定性。鲁棒控制的设计目标是抑制不确定性对控制性能的影响，包括外部干扰和模型误差。其中，处理外部干扰的目标是实现干扰抑制性能，应对模型误差的目标是保障系统鲁棒稳定。

       当同时考虑两种不确定性时，干扰抑制保障条件将引入不确定性，导致鲁棒性能问题是非凸优化和多目标优化难题。特别当动力学系统呈现非线性特性时，可行解空间的非凸区域产生潜在扩张，同时可能诱导性能函数呈现非连续、高曲率形态，为直接求解带来挑战。

图 1 鲁棒控制问题的非连续优化景观示意（Zheng et al. 2023）

       非线性鲁棒性能问题的传统求解思路包括线性化方法和耗散不等式。线性化方法首先利用线性化动力学模型，确定摄动参数区域顶点，消除干扰抑制保障条件的不确定性。将顶点采样结果代入线性化模型后，构建多个线性矩阵不等式（LMI）约束并联立求解，实现摄动参数区域内的干扰抑制性能。然而，线性化操作将导致控制性能趋于保守。此外，耗散理论指出，鲁棒性能问题可以通过包含模型误差项的不等式条件进行求解。这是含参数不确定的非线性偏微分不等式（PDI），缺乏成熟通用的数值求解方法。

图2 非线性鲁棒性能问题的传统求解思路

       鉴于鲁棒控制的控制输入和不确定性存在博弈关系，Başar 透过零和博弈视角，将线性鲁棒控制拓展到非线性系统。根据动态规划原理，求解零和博弈问题或干扰抑制问题的充分必要条件是哈密顿 - 雅可比 - 艾萨克斯（HJI）方程 或哈密顿 - 雅可比（HJ）不等式。由于这是典型的非线性偏微分方程，其解析解难以获得，因此，可以采用强化学习等数值方法进行求解。

       针对不确定性耦合的挑战，课题组的李杰博士通过分析模型误差边界对偏微分方程的影响，建立了保障干扰抑制性能的模型误差对消机制（如图3），提出了面向鲁棒性能的鲁棒策略迭代（RPI-P）算法。

图 3 保障干扰抑制性能的模型误差对消机制

       当非线性系统存在模型误差时，保障干扰抑制性能的 HJ 不等式被动地引入了误差项。为了对消影响，向 HJI 方程中主动添加对消项，建立确定性的增广 HJI 方程。利用增广 HJI 方程和 HJ 不等式的值函数解空间包含关系，保障干扰抑制性能对有界模型误差成立。

       以此为基础，进一步设计了求解增广 HJI 方程的 RPI-P 算法

       其中，第一部分使用历史状态作为批次数据，通过梯度下降法，近似增广 HJI 方程的解，同时实现持续学习；第二部分通过最小化李雅普诺夫函数的导数，增强训练过程中闭环系统的稳定性。通过经验回放和稳定项，该方法同时消除了持续激励条件和初始稳定控制器的要求。

       进一步分析算法的收敛性和稳定性，设计包含值函数权重误差和李雅普诺夫函数的联合函数

       为推动权重误差和系统状态x趋向原点，推导联合函数导数小于 0 的充分条件，得到权重误差或系统状态需大于等于某个边界λ。根据李雅普诺夫扩展定理，权重误差和系统状态最终收敛到如图4 所示的绿色方形集合内，由此证明了算法的收敛性和稳定性。此外，理论结果表明，引入历史数据可以降低权重误差的最终边界λ。

图 4 收敛性和稳定性分析示意

       考虑同时包含模型误差和外部干扰的非线性振荡器。将不同干扰信号应用于振荡器系统，并对两组模型不确定参数分别均匀采样 9 组结果。正交组合后，记录 81 组动力学模型的实际干扰抑制水平如图5 所示。

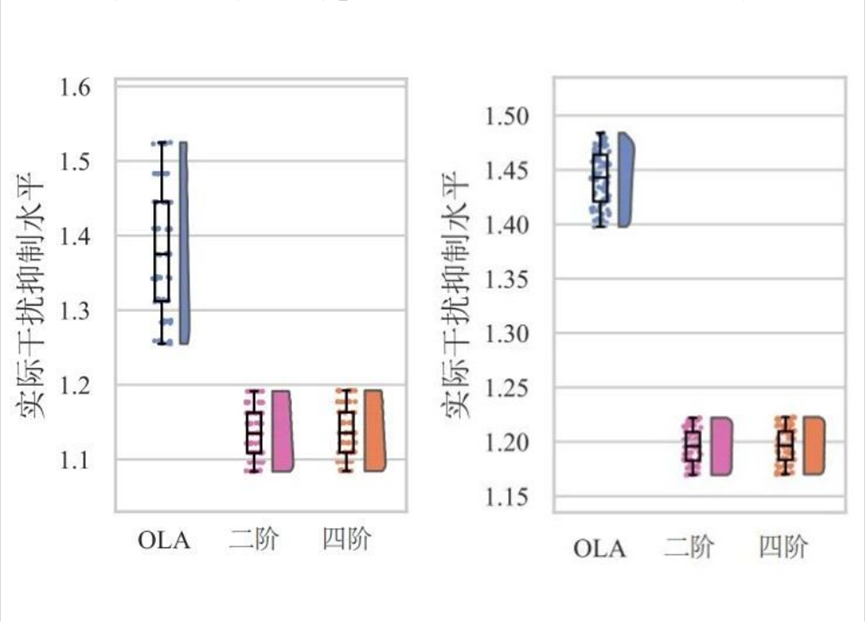
图 5 鲁棒性能验证结果：(a) 白噪声干扰；(b) 正弦干扰

       结果表明，不同近似函数训练得到的控制器具有相同的控制效果。和不考虑对消项的 OLA 方法对比，所提出方法的干扰抑制能力更强，且模型误差对其干扰抑制性能的影响更小，所提出方法的鲁棒性能更优。

       综上所述，研究构建了一类处理多源不确定性的增广 HJI 方程，该方程的解具有保障有界模型误差内干扰抑制性能的能力。同时提出了一种具有稳定性和收敛性保障的鲁棒强化学习方法，对非线性系统的鲁棒控制策略设计具有重要价值，为强化学习技术的落地应用奠定了理论基础。

       未来的研究将面向工程应用实际，针对多源不确定性导致智能汽车运动控制策略的鲁棒性能不足，设计算法同时应对外部干扰、模型误差和观测噪声，实现神经网络的鲁棒运动控制，并通过实车测试验证鲁棒运动控制策略的有效性。

参考文献

[1]Li J, Nagamune R, Zhang Y, Li S E. Robust approximate dynamic programming for nonlinear systems with both model error and external disturbance[J]. IEEE Transactions on Neural Networks and Learning Systems, 2025, 36(1): 896-910.

[2]Li J, Li S E, Duan J, et al. Relaxed policy iteration algorithm for nonlinear zero-sum games with application to H-infinity control[J]. IEEE Transactions on Automatic Control, 2024, 69(1): 426-433.

[3]Li S E. Reinforcement learning for sequential decision and optimal control[M]. Singapore: Springer Verlag, 2023.

[4]Duan J, Ren Y, Zhang F, Li J, et al. Encoding Distributional Soft Actor-Critic for Autonomous Driving in Multi-Lane Scenarios[J]. IEEE Computational Intelligence Magazine, 2024, 19(2): 96-112.

[5]T. Basar and P. Bernhard,  optimal control and related minimax design problems: a dynamic game approach. Springer Science & Business Media, 2008.