1.一元线性回归
算法原理
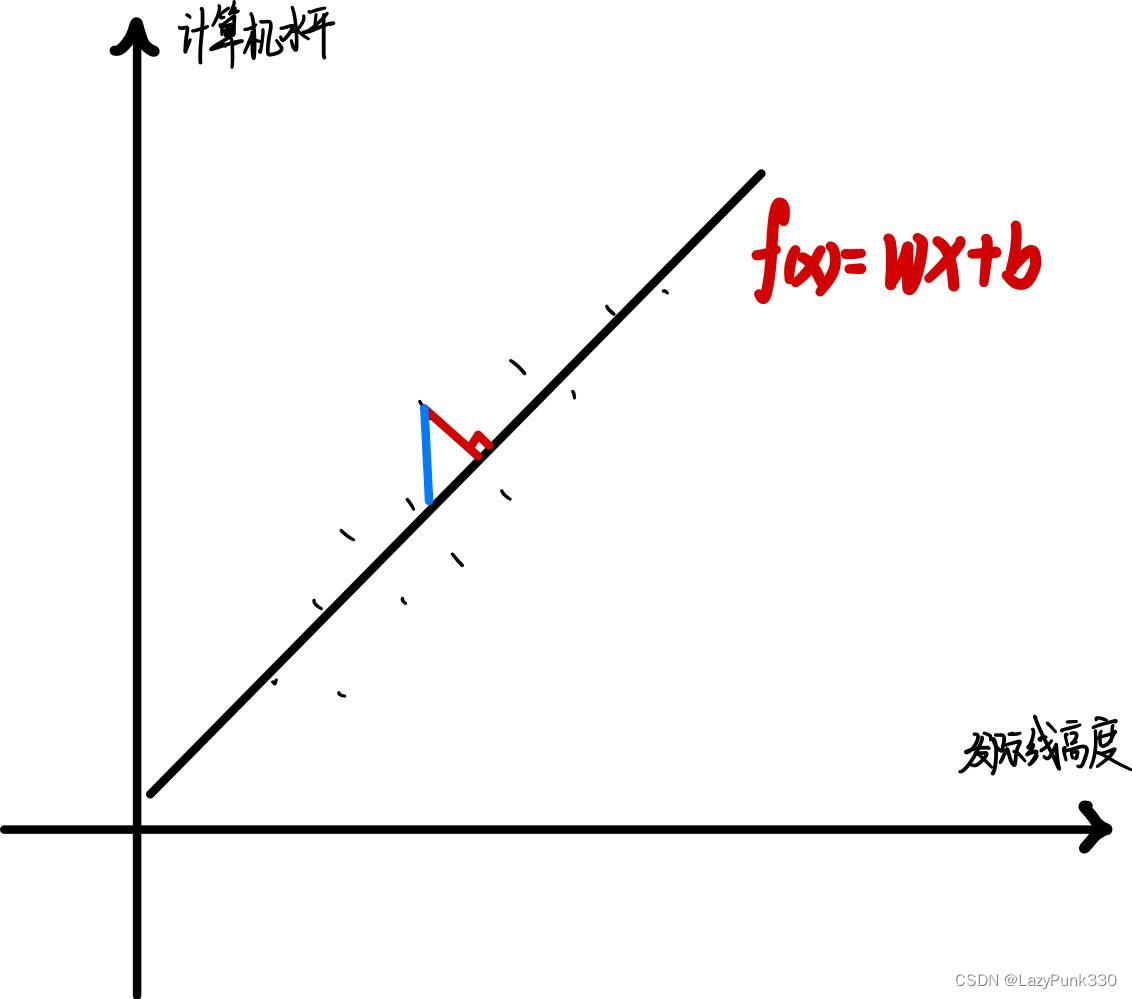
以发际线高度与计算机水平间的关系为例:
如图1所示,模型 f(x) = wx + b,拟合效果较好(若采用曲线形式拟合可能导致过拟合问题)。
该模型到各个点平行于Y轴的距离最短,称为“线性回归”。若到各个点的垂直距离最短则称为“正交回归”。
预测值y'与实际值y之间存在误差,称为“预测误差”,预测误差之和称为“均方误差”。可知线性回归即求均方误差最小的直线。
最小二乘估计
基于均方误差最小化进行模型求解的方法称为“最小二乘法”
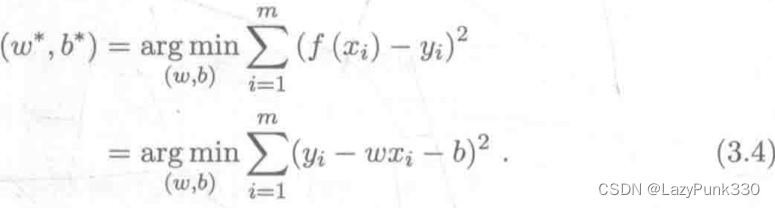
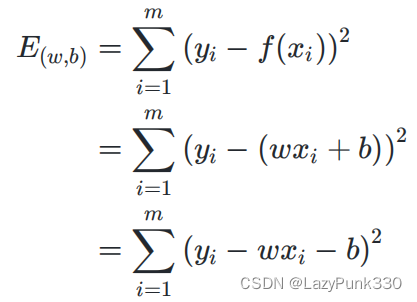
图3为图2中公式后半部分解释。
极大似然估计
极大似然估计用于估计概率分布的参数值。其直观想法为:使得观测样本出现概率最大的分布就是待求分布,即使得联合概率(似然函数)L()取到最大值的
'即为
的估计值。
因此有计算方法如下:对于离散型(或连续型)随机变量X,假设其概率质量函数为P(x;)(概率密度函数为p(x;
)),其中
为待估计的参数值(可以有多个)。现有x1, x2, x3, ..., xn是来自X的n个独立同分布的样本,他们的联合概率为:
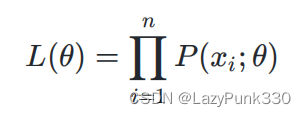
其中x1, x2, x3, ..., xn是已知量,是未知量,因此以上概率是一个关于
的函数,称L(
)为样本的似然函数。
例如:观测样本x1, x2, x3, ...,xn,服从某个正态分布X~N(,
),那么
,
为待估计的参数值,如果用极大似然估计法估计
,
,则有:
概率密度函数: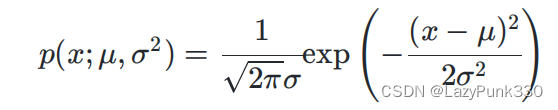
似然函数: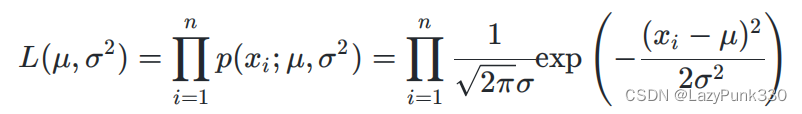
然后可以求出令L(,
)取得最大值的
,
但实际计算中因为对数函数ln是单调递增函数,所以lnL(,
)和原函数L(
,
)变化趋势相同,存在相同的最大值点,并且通过对数函数的性质可以化简L(
,
)中的连乘项,因此通常会用lnL(
,
)代替原函数求
,
,其运用如下:
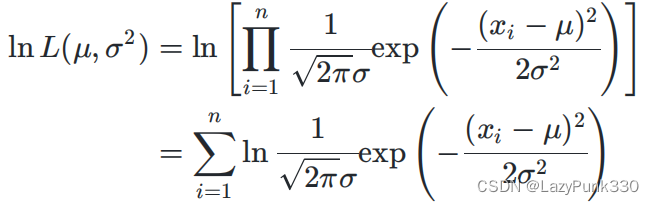
用极大似然估计推导线性回归方程
已知线性回归有以下模型:y = wx + b +
其中为不受控制的随机误差,通常假设其服从均值为0的正态分布
~N(0,
)(高斯提出,中心极限定理同样可证),所以有
的概率密度函数:

根据公式可用y -(wx + b)等价替换,有:
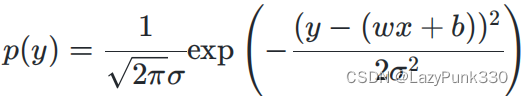
注:此处p(y)由正态分布推导得出,将y视作随机变量,wx + b等效为均值
即上式可看作y~N(wx + b,),下面用极大似然估计来估计w和b的值,似然函数为
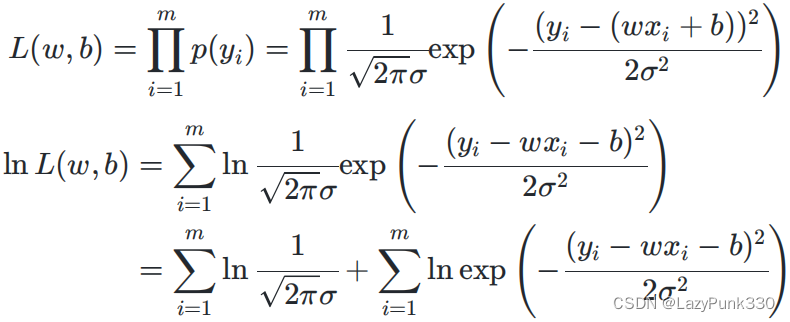
 因为m,
因为m,均为常数,所以最大化ln L(w,b)等价于最小化
,即
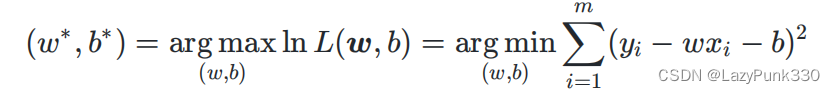
与最小二乘法得到的公式相同,说明极大似然估计法在这里等价于最小二乘估计。
求解w和b
求解w和b其本质上是一个多元函数求最值的问题,更具体来说是凸函数求最值的问题。
因此我们求解思路应为:先证明是关于w和b的凸函数,然后根据凸函数求最值的思路求解出w和b。
定理:设是非空开凸集(注1),
,且f(x)在
上二阶连续可微,如果f(x)的Hessian(海塞)矩阵(注4)在
上是半正定的,则f(x)是
上的凸函数。(类比一元函数判断凹凸性)
因此,只需证明的Hessin(海塞)矩阵
是半正定的,那么就是关于w和b的凸函数。

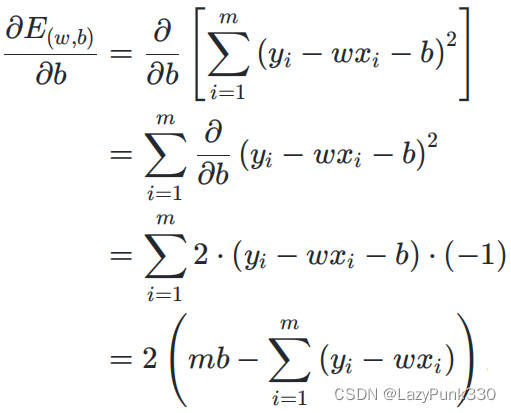
在公式3.5的基础上分别求对w的二阶偏导和对b的偏导得:


在公式3.6的基础上分别求对w的二阶偏导和对b的偏导得:

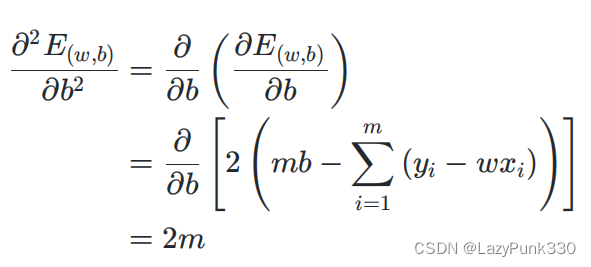
有
根据半正定矩阵的判定定理之一:若实对称矩阵的所有顺序主子式均为非负,则该矩阵为半正定矩阵。
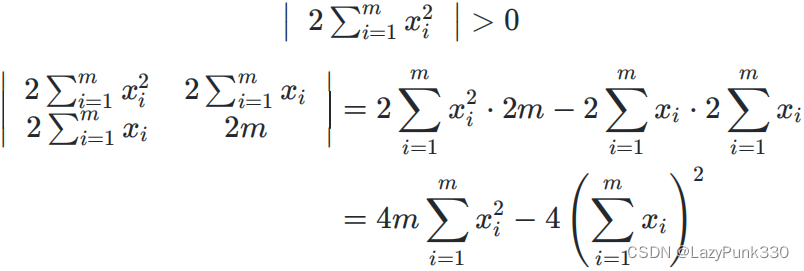
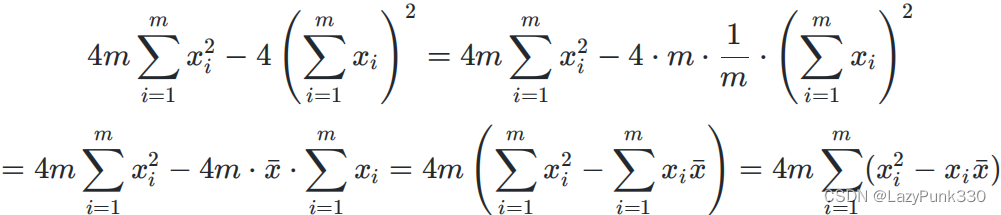
由于
所以有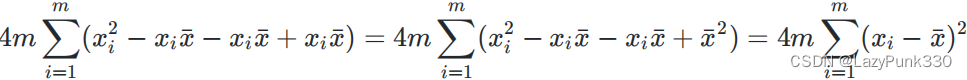
易知,Hessin(海塞矩阵)
的所有顺序主子式均非负,该矩阵为半正定矩阵,进而
是关于w和b的凸函数。
由凸充分性定理:若是凸函数,且f(x)一阶连续可微,则x'是全局解的充分必要条件是
所以,的点即为最小值点,即
由此可得

对公式3.8化简可得
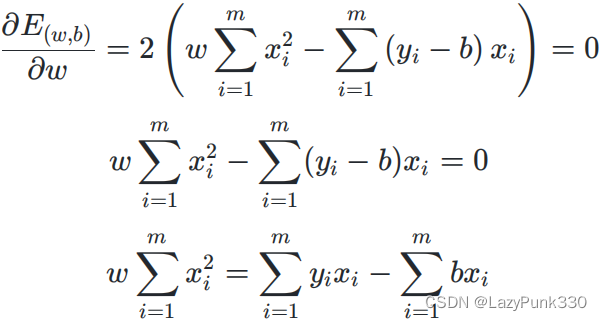
把代入得
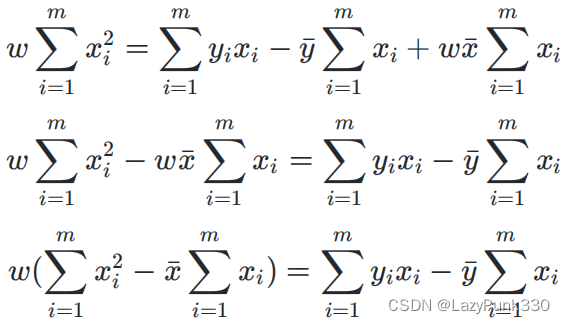
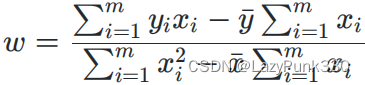
其中

代入可得

BTW
1.模型:根据具体问题,确定假设空间
2.策略:根据评价标准,确定选取最优模型的策略(通常会产出一个“损失函数”)
3.算法:求解损失函数,确定最优模型
补充
注1:凸集
设集合,如果对任意的
与任意的
,有
则称集合是凸集。凸集的几何意义为:若两个点属于此集合,则这两点连线上的任意一点均属于此集合(应补充图)。常见的凸集有空集
,n维欧氏空间
注2:凸函数
设是非空凸集,f是定义在
上的函数,如果对任意的
,
,均有
则称f为上的凸函数(应补充图)
注3:梯度(多元函数的一阶导数)
设n元函数f(x)对自变量的各分量
的偏导数
都存在,则称函数f(x)在x处一阶可导,并称向量
为函数f(x)在x处的一阶导数或梯度。
注4:Hessian(海塞)矩阵(多元函数的二阶导数)
设n元函数f(x)对自变量的各分量
的二阶偏导数
都存在,则称函数f(x)在x处二阶可导,并称矩阵

为函数f(x)在x处的二阶导数或Hessian(海塞)矩阵。
2.二分类线性判别分析
算法原理
从几何的角度,让全体训练样本经过投影后:
·异类样本的中心尽可能远。
·同类样本的方差尽可能小。
损失函数推导
经过投影后,异类样本的中心尽可能远(非严格投影)
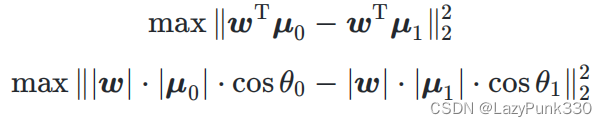
经过投影后,同类样本的方差尽可能小(非严格方差)
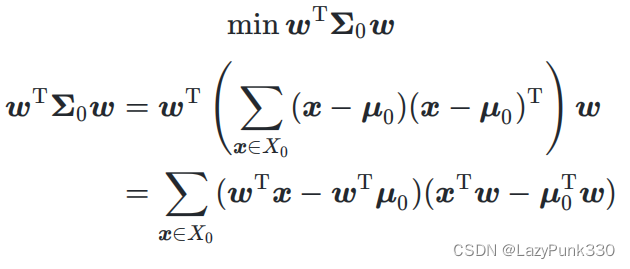

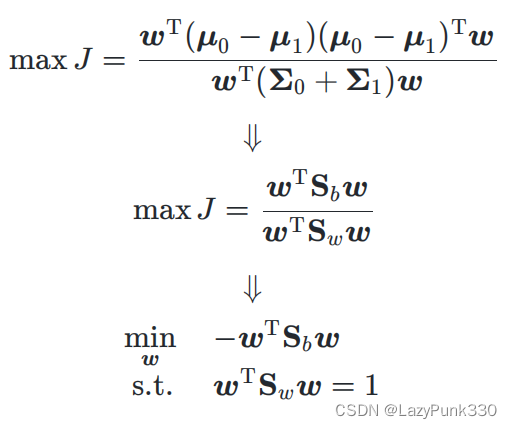
拉格朗日乘子法
对于金汉等式约束的优化问题,其中自变量,
和
均有连续的一阶连续偏导数。
列出其拉格朗日函数:
其中为拉格朗日乘子。然后对拉格朗日函数关于
求偏导,并令导数等于0再搭配约束条件
解出
,求解出的所有
即为上述优化问题的所有可能极值点
ps:解释为什么是

求解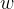
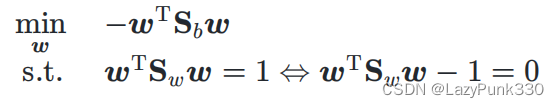
由拉格朗日乘子法可得拉格朗日函数为 :
对 求偏导可得:
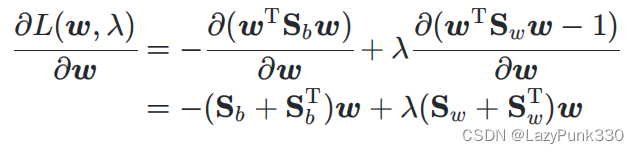
由于 所以有:
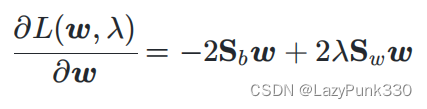
令上式等于0即可得:
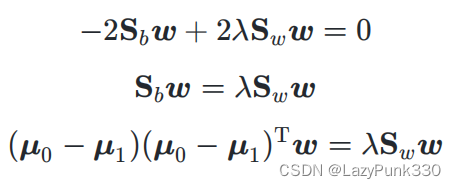
若令,则:
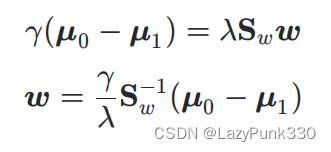
由于最终要求解的不关心其大小,仅关心其方向,所以
这个常数项可以任意取值,如西瓜书中所说“不妨令其
”等价于令
,进而使得
,此时求解出的
即为公式(3.39)(此处





















 124
124











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








