文章目录
- **激活函数?**
- Sigmoid
- **softsign**
- Tanh:双曲正切函数
- t a n h − 1 tanh^{-1} tanh−1:反正切函数
- ISRU: 反平方根函数
- ReLU
- ReLU 变种
- **softplus**
- GLU函数+GTU函数
- APL:自适应分段线性函数
- 弯曲恒等函数
- SoftExponential
- 正弦函数
- Sinc函数
- 高斯函数
- ACON:(**Ac**tivate **O**r **N**ot)激活函数
- Swish
- Maxout
- hard-Swish
- **EliSH**与**HardEliSH**
- Mish
- Softmax
- shrink系列
- hard系列:
- 激活函数的作用
- 梯度消失与梯度爆炸
- 激活函数选择
- 总结
- reference
激活函数?
激活函数(Activation Function),就是在人工神经网络的神经元上运行的函数,负责将神经元的输入映射到输出端。
使用非线性的激活函数将非线性特性引入到到网络中。
激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
一个节点的激活函数(Activation Function)定义了该节点在给定的输入或输入的集合下的输出。神经网络中的激活函数用来提升网络的非线性(只有非线性的激活函数才允许网络计算非平凡问题),以增强网络的表征能力。对激活函数的一般要求是:必须非常数、有界、单调递增并且连续,并且可导。
在实际选择激活函数时并不会严格要求可导,只需要激活函数几乎在所有点可导即可,即在个别点不可导是可以接受的。另外,其导数尽可能的大可以帮助加速训练神经网络,否则导数过小会导致网络无法继续训练下去。
Sigmoid
函数式:
f
(
x
)
=
1
1
+
e
−
x
f(x) = \frac{1}{1+e^{-x}}
f(x)=1+e−x1
求导:
f
(
x
)
=
(
1
+
e
−
x
)
−
1
f
′
(
x
)
=
−
1
∗
(
1
+
e
−
x
)
−
2
∗
(
1
+
e
−
x
)
′
=
(
1
+
e
−
x
)
−
2
∗
e
−
x
=
1
+
e
−
x
−
1
(
1
+
e
−
x
)
2
=
1
+
e
−
x
(
1
+
e
−
x
)
2
−
1
(
1
+
e
−
x
)
2
=
1
1
+
e
−
x
−
1
(
1
+
e
−
x
)
2
=
1
1
+
e
−
x
∗
(
1
−
1
1
+
e
−
x
)
=
f
(
x
)
∗
(
1
−
f
(
x
)
)
\begin{equation} \begin{aligned} f(x) &= (1+e^{-x})^{-1} \\ f'(x) &= -1 *(1+e^{-x})^{-2} * (1+e^{-x})' \\ &=(1+e^{-x})^{-2} * e^{-x} \\ &= \frac{1+e^{-x}-1}{(1+e^{-x})^2} \\ &= \frac{1+e^{-x}}{(1+e^{-x})^2} - \frac{1}{(1+e^{-x})^2} \\ &= \frac{1}{1+e^{-x}} - \frac{1}{(1+e^{-x})^2} \\ &= \frac{1}{1+e^{-x}} * (1 - \frac{1}{1+e^{-x}}) \\ &= f(x) * (1-f(x)) \end{aligned} \end{equation}
f(x)f′(x)=(1+e−x)−1=−1∗(1+e−x)−2∗(1+e−x)′=(1+e−x)−2∗e−x=(1+e−x)21+e−x−1=(1+e−x)21+e−x−(1+e−x)21=1+e−x1−(1+e−x)21=1+e−x1∗(1−1+e−x1)=f(x)∗(1−f(x))
优势是能够控制数值的幅度,在深层网络中可以保持数据幅度不会出现大的变化;而ReLU不会对数据的幅度做约束。
问题:
- 饱和的神经元会"杀死"梯度,指离中心点较远的x处的导数接近于0,容易就会出现梯度消失的情况,停止反向传播
- sigmoid函数在变量取绝对值非常大的正值或负值时会出现饱和现象,意味着函数会变得很平,并且对输入的微小改变会变得不敏感。的学习过程。
- sigmoid的输出不是以0为中心,而是0.5,这样在求权重w的梯度时,梯度总是正或负的。
- 指数计算耗时
Sigmoid Weighted Liner Unit(SiLU)
Swish包含了SiLU,换句话说SiLU是Swish的一种特例:
f
(
x
)
=
x
⋅
σ
(
x
)
f
′
(
x
)
=
f
(
x
)
+
σ
(
x
)
(
1
−
f
(
x
)
)
f(x)=x\cdot \sigma(x) \qquad\qquad f^{'}(x)=f(x)+\sigma(x)(1-f(x))
f(x)=x⋅σ(x)f′(x)=f(x)+σ(x)(1−f(x))

softsign
数学表达式:
f
(
x
)
=
x
1
+
∣
x
∣
f(x)=\frac{x}{1+|x|}
f(x)=1+∣x∣x
导数:
f
′
(
x
)
=
1
(
1
+
∣
x
∣
)
2
f'(x)=\frac{1}{(1+|x|)^2}
f′(x)=(1+∣x∣)21
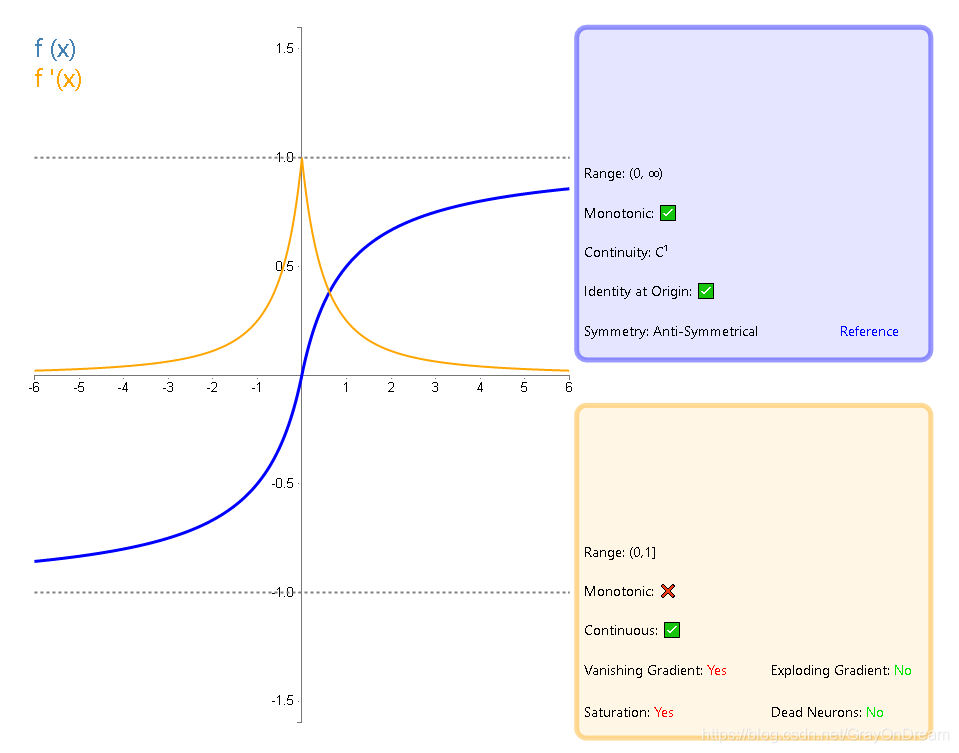
Tanh:双曲正切函数
函数式:
t
a
n
h
(
x
)
=
e
x
−
e
−
x
e
x
+
e
−
x
tanh(x) = \frac{e^x - e^{-x}}{e^x+e^{-x}}
tanh(x)=ex+e−xex−e−x
tanh 函数是sigmoid函数的一种变体,以0点为中心。取值范围为 [-1,1] ,而不是sigmoid函数的 [0,1] 。
你可能会想平移使得曲线以0点为中心,那么为什么还要收缩呢? 如果不拉伸或收缩得到 f ( x ) = e x − 1 e x + 1 f(x)={e^x-1\over e^x+1} f(x)=ex+1ex−1
求导:
t
a
n
h
′
(
x
)
=
[
(
e
x
−
e
−
x
)
∗
(
e
x
+
e
−
x
)
−
1
]
′
=
(
e
x
−
e
−
x
)
′
∗
(
e
x
+
e
−
x
)
−
1
+
[
(
e
x
+
e
−
x
)
−
1
]
′
∗
(
e
x
−
e
−
x
)
=
(
e
x
+
e
−
x
)
∗
(
e
x
+
e
−
x
)
−
1
−
(
e
x
+
e
−
x
)
−
2
∗
(
e
x
−
e
−
x
)
∗
(
e
x
−
e
−
x
)
=
1
−
(
e
x
−
e
−
x
)
2
(
e
x
+
e
−
x
)
2
=
1
−
tanh
(
x
)
2
\begin{equation} \begin{aligned} tanh'(x) &= [(e^x-e^{-x}) * (e^x + e^{-x})^{-1}]' \\ &= (e^x-e^{-x})'*(e^x + e^{-x})^{-1} + [(e^x + e^{-x})^{-1}]' * (e^x - e^{-x}) \\ &= (e^x + e^{-x}) * (e^x + e^{-x})^{-1} - (e^x + e^{-x})^{-2} * (e^x - e^{-x}) * (e^x - e^{-x}) \\ &= 1 - \frac{(e^x - e^{-x})^2}{(e^x+e^{-x})^2} \\ &= 1 - \tanh{(x)}^2 \end{aligned} \end{equation}
tanh′(x)=[(ex−e−x)∗(ex+e−x)−1]′=(ex−e−x)′∗(ex+e−x)−1+[(ex+e−x)−1]′∗(ex−e−x)=(ex+e−x)∗(ex+e−x)−1−(ex+e−x)−2∗(ex−e−x)∗(ex−e−x)=1−(ex+e−x)2(ex−e−x)2=1−tanh(x)2
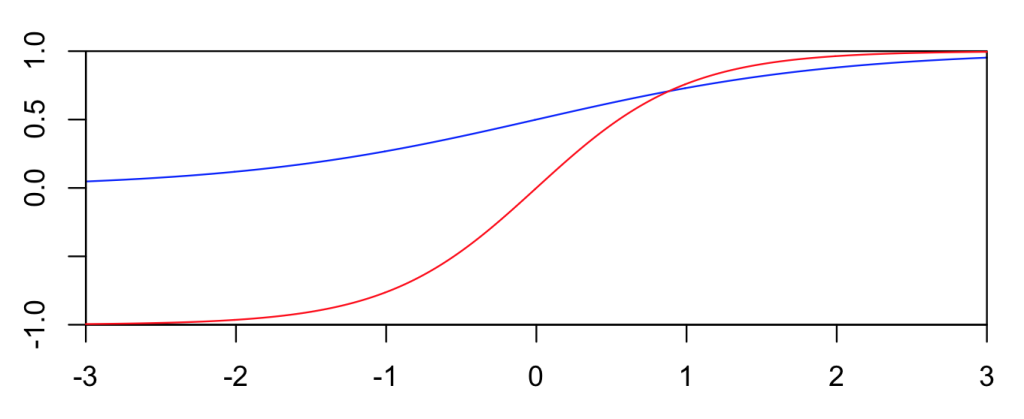
-
梯度消失问题程度
tanh ′ ( x ) = 1 − tanh ( x ) 2 ∈ ( 0 , 1 ) \tanh'( x ) = 1-\tanh( x )^2 \in (0,1) tanh′(x)=1−tanh(x)2∈(0,1)sigmoid: s ′ ( x ) = s ( x ) × ( 1 − s ( x ) ) ∈ ( 0 , 1 / 4 ) \text{sigmoid: } s'(x)=s(x)\times(1-s(x))\in(0,1/4) sigmoid: s′(x)=s(x)×(1−s(x))∈(0,1/4)
可以看出 t a n h ( x ) tanh(x) tanh(x)的梯度消失问题比 s i g m o i d sigmoid sigmoid要轻。梯度如果过早消失,收敛速度较慢。
-
以零为中心的影响
如果当前参数 ( w 0 , w 1 ) (w_0,w_1) (w0,w1)的最佳优化方向是 ( + d 0 , − d 1 ) (+d_0, -d_1) (+d0,−d1),则根据反向传播计算公式,我们希望$ x_0 和 和 和 x_1$ 符号相反。但是如果上一级神经元采用 Sigmoid 函数作为激活函数,sigmoid不以0为中心,输出值恒为正,那么我们无法进行最快的参数更新,而是走 Z 字形逼近最优解。[4]
tanh仍然存在梯度饱和与exp计算复杂的问题。
t a n h − 1 tanh^{-1} tanh−1:反正切函数
f
(
x
)
=
t
a
n
−
1
(
x
)
f
′
(
x
)
=
1
x
2
+
1
f(x)=tan^{-1}(x)\qquad\qquad f^{'}(x)=\frac{1}{x^2+1}
f(x)=tan−1(x)f′(x)=x2+11

ISRU: 反平方根函数
f ( x ) = x 1 + α x 2 f ′ ( x ) = ( 1 1 + α x 2 ) 3 f(x)=\frac{x}{\sqrt{1+\alpha x^2}}\qquad \qquad f^{'}(x)=(\frac{1}{\sqrt{1+\alpha x^2}})^3 f(x)=1+αx2xf′(x)=(1+αx21)3
ReLU
paper: Deep Sparse Rectifier Neural Networks
函数式:
f
(
x
)
=
max
(
0
,
x
)
f(x) = \max{(0,x)} \\
f(x)=max(0,x)
求导:
y
=
{
1
,
x
≥
0
0
,
x
<
0
y= \begin{cases} 1,\quad x\geq 0\\ 0, \quad x<0 \end{cases}
y={1,x≥00,x<0
1.ReLU解决了梯度消失的问题,至少x在正区间内,神经元不会饱和。
2.由于ReLU线性、非饱和的形式,在SGD中能够快速收敛。
3.计算速度要快很多。ReLU函数只有线性关系,不需要指数计算,不管在前向传播还是反向传播,计算速度都比sigmoid和tanh快。
ReLU 的稀疏性(摘自这里):
当前,深度学习一个明确的目标是从数据变量中解离出关键因子。原始数据(以自然数据为主)中通常缠绕着高度密集的特征。然而,如果能够解开特征间缠绕的复杂关系,转换为稀疏特征,那么特征就有了鲁棒性(去掉了无关的噪声)。稀疏特征并不需要网络具有很强的处理线性不可分机制。那么在深度网络中,对非线性的依赖程度就可以缩一缩。一旦神经元与神经元之间改为线性激活,网络的非线性部分仅仅来自于神经元部分选择性激活。
对比大脑工作的 95% 稀疏性来看,现有的计算神经网络和生物神经网络还是有很大差距的。庆幸的是,ReLu 只有负值才会被稀疏掉,即引入的稀疏性是可以训练调节的,是动态变化的。只要进行梯度训练,网络可以向误差减少的方向,自动调控稀疏比率,保证激活链上存在着合理数量的非零值。
ReLU 缺点
- 坏死: ReLU 强制的稀疏处理会减少模型的有效容量(即特征屏蔽太多,导致模型无法学习到有效特征)。由于 ReLU 在 x <0 时梯度为 0,这样就导致负的梯度在这个 ReLU 被置零,而且这个神经元有可能再也不会被任何数据激活,称为神经元 “坏死”。
- 无负值: ReLU 和 sigmoid 的一个相同点是结果是正值,没有负值。
ReLU 变种
Noisy ReLU[1]
ReLU可以被扩展以包括高斯噪声(Gaussian noise):
f
(
x
)
=
max
(
0
,
x
+
Y
)
,
Y
∼
N
(
0
,
σ
(
x
)
)
f(x)=\max(0,x+Y), Y\sim N(0,\sigma(x))
f(x)=max(0,x+Y),Y∼N(0,σ(x))
Noisy ReLU 在受限玻尔兹曼机解决计算机视觉任务中得到应用。
Leaky-ReLU和RReLU
带泄露线性整流函数(Leaky-ReLU) paper: Rectifier Nonlinearities Improve Neural Network Acoustic Models
函数式:
f
(
x
)
=
{
x
,
x
≥
0
x
α
,
x
<
0
\begin{equation} f(x)= \begin{cases} x, & \text{$x\geq 0$}\\ x \over\alpha, & \text{$x < 0$} \end{cases} \end{equation}
f(x)={x,α,xx≥0x<0
求导:
f
′
(
x
)
=
{
1
,
x
≥
0
1
α
,
x
<
0
\begin{equation} f'(x)= \begin{cases} 1, & \text{$x\geq 0$}\\ 1 \over\alpha, & \text{$x < 0$} \end{cases} \end{equation}
f′(x)={1,α,1x≥0x<0
当固定为
α
∈
(
1
,
+
∞
)
\alpha \in (1,+\infty)
α∈(1,+∞)时,是Leaky ReLU。
当 α \alpha α服从高斯分布中随机产生时称为Random Rectifier(RReLU:带泄露随机线性整流函数), α ∼ U ( l , u ) , l < u ; l , u ∈ [ 0 , 1 ) \alpha \sim U(l,u),l<u;l,u \in [0,1) α∼U(l,u),l<u;l,u∈[0,1)
“随机纠正线性单元”RReLU也是Leaky ReLU的一个变体。在RReLU中,负值的斜率在训练中是随机的,在之后的测试中就变成了固定的了。RReLU的亮点在于,在训练环节中, α \alpha α是从一个均匀的分布 U ( l , u ) U(l,u) U(l,u)中随机抽取的数值。起到了一定的正则化效果。
优点:
- 不会过拟合(saturate)
- 计算简单有效
- 比sigmoid/tanh收敛快
缺点:
1.Leaky ReLU函数中的 α \alpha α需要通过先验知识人工赋值。
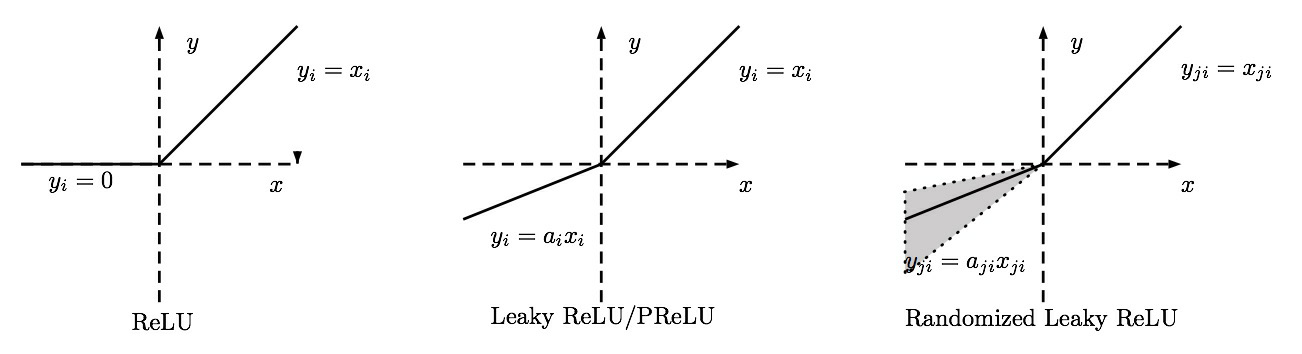
PReLU:参数化线性整流函数
何凯明paper 《Delving Deep into Rectifiers:Surpassing Human-Level Performance on ImageNet Classification》
参数整流线性单元(Parametric Rectified linear unit,PReLU),用来解决ReLU带来的神经元坏死的问题。当
x
<
0
x<0
x<0时,
f
(
x
)
=
α
x
f(x)=\alpha x
f(x)=αx,其中
α
\alpha
α非常小,这样可以避免在
x
<
0
x<0
x<0时,不能够学习的情况:
f
(
x
i
)
=
m
a
x
(
α
i
x
i
,
x
i
)
f(x_i)=max(α_ix_i,x_i)
f(xi)=max(αixi,xi)
其中 α i \alpha_i αi不是固定的超参数,而是通过反向传播学习出来的, i i i表示不同通道,默认是对所有通道的,如果参数有通道数,则不同的a是对应不同通道。
论文中 α i \alpha_i αi被初始化为0.25
Leaky ReLU α \alpha α是固定的; PReLU 的 α \alpha α不是固定的, 通过训练得到; RReLU 的 α \alpha α是从一个高斯分布中随机产生, 并且在测试时为固定值,与 Noisy ReLU 类似(但是区间正好相反)。
ReLU 系列对比:
CLASStorch.nn.PReLU(num_parameters=1, init=0.25, device=None, dtype=None)
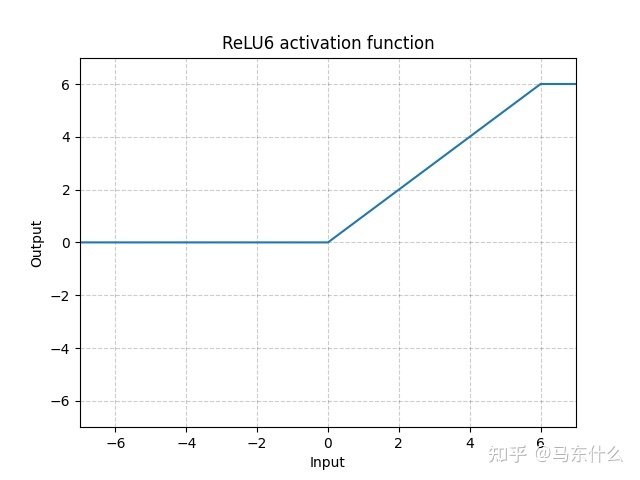
ReLU6
paper: MobileNetV2: Inverted Residuals and Linear Bottlenecks
ReLU 相比 sigmoid 和 tanh 没有对上界设限。 在实际使用中, 可以设置一个上限, 参考这个上限的来源论文: Convolutional Deep Belief Networks on CIFAR-10. A. Krizhevsky
函数式:
R
e
L
U
6
(
x
)
=
m
i
n
(
6
,
m
a
x
(
0
,
x
)
)
ReLU6(x)=min(6,max(0,x))
ReLU6(x)=min(6,max(0,x))
即当 x > 6时,其导数也为0。
求导:
R
e
L
U
6
′
(
x
)
=
{
1
,
0
≤
x
≤
6
0
,
o
t
h
e
r
s
ReLU6'(x)= \begin{cases} 1,\quad 0\leq x\leq 6\\ 0, \quad others \end{cases}
ReLU6′(x)={1,0≤x≤60,others
relu6的好处:
1)可以让模型更早地学到稀疏特征(相对于relu而言,更容易出现权重不更新的现象,因为取值一旦小于0或超过6,则权重停止更新,直接输出常数0或6,训练的过程中可能出现的情况就是有用的输入特征和权重不断得到更新,无用的特征和权重停止更新输出常数,ps:relu也是可以学到稀疏特征的);
2)可以防止数值爆炸。
3)增强浮点数的小数位表达能力。因为整数位最大是6,所以只占3个bit,其他bit全部用来表达小数位。
ELU:指数线性单元
f ( x ) = { α ( e x − 1 ) , x ≤ 0 x , x > 0 \begin{equation} f(x)= \begin{cases} \alpha(e^x-1), & \text{$x\leq 0$} \\ x, & \text{$x\gt 0$} \end{cases} \end{equation} f(x)={α(ex−1),x,x≤0x>0
f ′ ( x ) = { f ( x ) + α , x ≤ 0 1 , x > 0 \begin{equation} f'(x)= \begin{cases} f(x)+\alpha, & \text{$x\leq 0$} \\ 1, & \text{$x\gt 0$} \end{cases} \end{equation} f′(x)={f(x)+α,1,x≤0x>0
exponential linear unit, (Fastand accurate deep network learning by exponential linear units (elus))该激活函数由 Djork 等人提出, 被证实有较高的噪声鲁棒性, 同时能够使得使得神经元
的平均激活均值趋近为 0, 同时对噪声更具有鲁棒性。这里的
α
\alpha
α是一个人工指定的超参数。
优点:
- ELU包含了ReLU的所有优点。
- 神经元不会出现死亡的情况。
- ELU激活函数的输出均值是接近于零的。
缺点:由于需要计算指数, 计算量较大。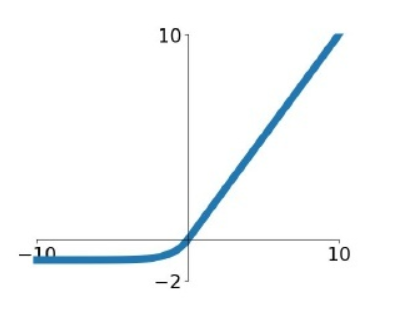
SELU:扩展指数线性函数
论文: 自归一化神经网络 (Self-Normalizing Neural Networks) 中提出只需要把激活函数换成 SELU 就能使得输入在经过一定层数之后变成固定的分布。 参考对这篇论文的讨论.
SELU 是给 ELU 乘上系数 λ, 即
S
E
L
U
(
x
)
=
λ
⋅
E
L
U
(
x
)
\rm{SELU}(x)=\lambda\cdot \rm{ELU}(x)
SELU(x)=λ⋅ELU(x)
f
(
x
)
=
λ
{
α
(
e
x
−
1
)
x
≤
0
x
x
>
0
f(x)=\lambda \begin{cases} \alpha(e^x-1) & x \le 0 \\ x & x>0 \end{cases}
f(x)=λ{α(ex−1)xx≤0x>0
其中 λ \lambda λ:1.0507009873554804934193349852946
α \alpha α:1.6732632423543772848170429916717
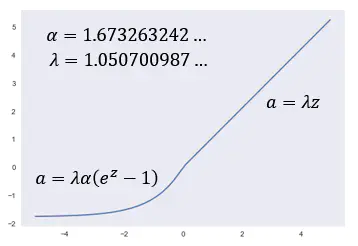
SELU 必须使用 LeCun Normal 的权重初始化方法,如果要使用 dropout,则必须使用称为 Alpha Dropout 的特殊版本。
特点:
- 它的值有正有负:在整个ReLU的family里里面,除了一开始最原始的ReLU以外都有负值,所以这个特性还好;
- 有 Saturation Region:其他的ReLU他们没有Saturation Region(饱和阶段),但是他有Saturation Region,不过ELU其实也有Saturation Region,因为SELU就只是ELU乘上一个 λ \lambda λ而已;乘上这个有 λ \lambda λ什么不同?乘上 λ \lambda λ,让它在某些区域的斜率是大于1的,意味着说你进来一个比较小的变化,通过Region以后,他把你的变化放大1.0507700987倍,所以它的input能是会被放大的,而且这是他一个ELU的没有的特色。
代码:
def selu(x):
with ops.name_scope('elu') as scope:
alpha = 1.6732632423543772848170429916717
scale = 1.0507009873554804934193349852946
return scale*tf.where(x>0.0,x,alpha*tf.nn.elu(x))
GELU:高斯误差线性单元
GELU(高斯误差线性单元)是一个非初等函数形式的激活函数,是 RELU 的变种。由 16 年论文 Gaussian Error Linear Units (GELUs) 提出,随后被 GPT-2、BERT、RoBERTa、ALBERT 等 NLP 模型所采用。论文中不仅提出了 GELU 的精确形式,还给出了两个初等函数的近似形式。函数曲线如下:
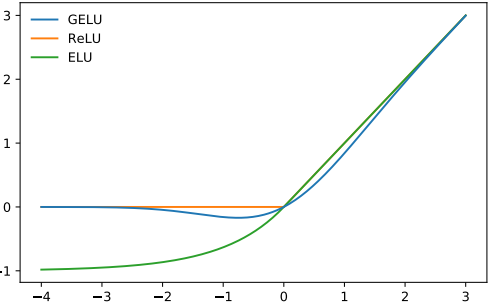
GELU ( μ = 0 , σ = 1 \mu=0, \sigma=1 μ=0,σ=1), ReLU and ELU ( α = 1 \alpha=1 α=1)
dropout思想和relu的结合,对于linear层的每一个输出,假设linear层的输出服从标准正态分布,使用标准正态分布的累积概率函数计算单个输出的概率值,然后使用一个伯努利分布
G
E
L
U
(
x
)
=
x
P
(
X
≤
x
)
=
x
Φ
(
x
)
\begin{align} GELU(x)&=xP(X \leq x)=x \Phi(x)\end{align}
GELU(x)=xP(X≤x)=xΦ(x)
产生随机产生1或0,和relu不同的地方在于,relu对于小于0的输出是置0的,而GELU则是有一定的概率不置0。
RELU 及其变种与 Dropout 从两个独立的方面来决定网络的输出,为了把两者合二为一,在网络正则化方面,Dropout 将神经单元输出随机置 0(乘 0),Zoneout 将 RNN 的单元随机跳过(乘 1)。两者均是将输出乘上了服从伯努利分布(二项分布)的变量 m ~ Bernoulli§,其中 p 是指定的确定的参数,表示取 1 的概率。
论文中希望 p 能够随着输入 x 的不同而不同,在 x 较小时以较大概率将其置 0。 由于神经元的输入通常服从正态分布,尤其是在加入了 Batch Normalization 的网络中,因此令 p 等于正态分布的累积分布函数即可满足。正态分布的概率密度函数:
f
(
x
)
=
1
σ
2
π
e
−
(
x
−
μ
)
2
2
σ
2
f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}\;e^{-{\frac {\left(x-\mu \right)^{2}}{2\sigma ^{2}}}}
f(x)=σ2π1e−2σ2(x−μ)2
累积分布函数:
F
(
x
)
=
1
σ
2
π
∫
−
∞
x
exp
(
−
(
t
−
μ
)
2
2
σ
2
)
d
t
F(x) = \frac{1}{\sigma\sqrt{2\pi}} \int_{-\infty}^x \exp \left( -\frac{(t - \mu)^2}{2\sigma^2} \ \right)\, dt
F(x)=σ2π1∫−∞xexp(−2σ2(t−μ)2 )dt
正态分布的累积分布函数曲线与 sigmoid 曲线相似。
假设输入服从标准正态分布: X ∼ N ( 0 , 1 ) X\sim \mathcal N(0,1) X∼N(0,1),标准正态分布的累积分布函数习惯上记为 Φ ( x ) = P ( X ≤ x ) \Phi(x)=P(X\le x) Φ(x)=P(X≤x)
然而激活函数由于在训练和测试时使用方式完全相同,所以是需要有确定性的输出,这点与 Dropout 不同(Dropout 在测试时并不随机置 0)。由于概率分布的数学期望是确定值,因此改为求输出的期望: E [ m x ] = x E [ m ] = x Φ ( x ) E[mx]=xE[m]=x\Phi(x) E[mx]=xE[m]=xΦ(x),即对输入乘上伯努利分布的期望值 p = Φ ( x ) p=\Phi(x) p=Φ(x)
Φ
(
x
)
=
1
2
π
∫
−
∞
x
exp
(
−
t
2
2
)
d
t
=
1
2
+
1
2
π
∫
0
x
exp
(
−
t
2
2
)
d
t
=
1
2
(
1
+
2
π
∫
0
x
exp
(
−
(
t
2
)
2
)
d
t
2
)
=
1
2
(
1
+
2
π
∫
0
x
2
exp
(
−
z
2
)
d
z
)
=
1
2
(
1
+
e
r
f
(
x
2
)
)
\begin{align} \Phi(x) =& \frac{1}{\sqrt{2\pi}} \int_{-\infty}^x \exp\left(-\frac{t^2}{2}\right) \, dt \\ =& {1\over 2} + \frac{1}{\sqrt{2\pi}} \int_0^x \exp\left(-\frac{t^2}{2}\right) \, dt \tag{正态分布曲线下面积为1,一半则为0.5} \\ =& {1\over 2}\left(1 + \frac{2}{\sqrt{\pi}} \int_0^x \exp\left(-({t\over \sqrt 2})^2\right) \, {dt\over \sqrt 2}\right) \\ =& {1\over 2}\left(1 + \frac{2}{\sqrt{\pi}} \int_0^{x\over\sqrt 2} \exp\left(-z^2\right) \, dz\right) \\ =& {1\over 2}\left(1+\rm{erf}\left({x\over \sqrt 2}\right)\right) \end{align}
Φ(x)=====2π1∫−∞xexp(−2t2)dt21+2π1∫0xexp(−2t2)dt21(1+π2∫0xexp(−(2t)2)2dt)21(1+π2∫02xexp(−z2)dz)21(1+erf(2x))(正态分布曲线下面积为1,一半则为0.5)
其中的变换包含这个等式:
1
n
∫
0
x
f
(
t
/
n
)
d
t
=
∫
0
x
/
n
f
(
t
)
d
t
{1\over n}\int_0^x f(t/n)dt=\int_0^{x/n}f(t)dt
n1∫0xf(t/n)dt=∫0x/nf(t)dt,将x看作一个固定值,则不难理解。
在数学中,误差函数(也称之为高斯误差函数)定义如下:
erf
(
x
)
=
1
π
∫
−
x
x
e
−
t
2
d
t
=
2
π
∫
0
x
e
−
t
2
d
t
{\operatorname {erf} (x)={\frac {1}{\sqrt {\pi }}}\int _{-x}^{x}e^{-t^{2}}\,\mathrm {d} t={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,\mathrm {d} t}
erf(x)=π1∫−xxe−t2dt=π2∫0xe−t2dt
e
r
f
(
x
)
erf(x)
erf(x) 与 $tanh(x) $比较接近,与
2
(
σ
(
x
)
−
1
2
)
2\left(\sigma(x)-\frac{1}{2}\right)
2(σ(x)−21) 也有相似的曲线,但是相对差别较大一些。在代码实现中可以用近似函数来拟合
e
r
f
(
x
)
erf(x)
erf(x)。论文给出的两个近似如下:
x
Φ
(
x
)
≈
x
σ
(
1.702
x
)
x
Φ
(
x
)
≈
1
2
x
[
1
+
tanh
(
2
π
(
x
+
0.044715
x
3
)
)
]
\begin{align} x\Phi(x) &\approx x\sigma(1.702 x) \\ x\Phi(x) &\approx \frac{1}{2} x \left[1 + \tanh\left(\sqrt{\frac{2}{\pi}}\left(x + 0.044715 x^3\right)\right)\right] \end{align}
xΦ(x)xΦ(x)≈xσ(1.702x)≈21x[1+tanh(π2(x+0.044715x3))]
不过很多框架已经有精确的 erf 计算函数了,可以直接使用,参考代码如下:
# GPT-2 的 GELU 实现
def gelu(x):
return 0.5*x*(1+tf.tanh(np.sqrt(2/np.pi)*(x+0.044715*tf.pow(x, 3))))
# BERT 的 GELU 实现
def gelu(input_tensor):
cdf = 0.5 * (1.0 + tf.erf(input_tensor / tf.sqrt(2.0)))
return input_tesnsor*cdf
GELU vs Swish
GELU 与 Swish 激活函数(x · σ(βx))的函数形式和性质非常相像,一个是固定系数 1.702,另一个是可变系数 β(可以是可训练的参数,也可以是通过搜索来确定的常数),两者的实际应用表现也相差不大。
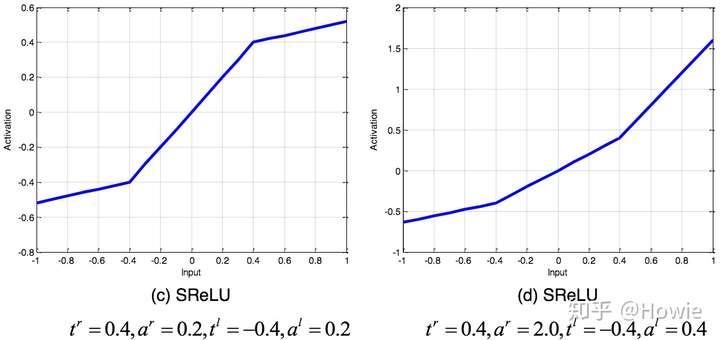
SReLU:S型线性整流激活函数
**SReLU(S-shaped Rectified Linear Activation Unit,S型修正线性激活单元)**由三个分段线性函数组成。系数作为参数,将在网络训练中学习(paper: Deep Learning with S-shaped Rectified Linear Activation Units)。
f
t
l
,
a
l
,
t
r
,
a
r
(
x
)
=
{
t
l
+
a
l
(
x
−
t
l
)
,
x
≤
t
l
x
,
t
l
≤
x
≤
t
r
t
r
+
a
r
(
x
−
t
r
)
,
x
≥
t
r
f_{t_l,a_l,t_r,a_r}(x)= \begin{cases} t_l+a_l(x-t_l),\quad x\leq t_l\\ x, \quad t_l \leq x \leq t_r\\ t_r+a_r(x-t_r), \quad x\geq t_r \end{cases}
ftl,al,tr,ar(x)=⎩
⎨
⎧tl+al(x−tl),x≤tlx,tl≤x≤trtr+ar(x−tr),x≥tr
值域:
(
−
∞
,
+
∞
)
(-\infty, +\infty)
(−∞,+∞)
ISRLU:反平方根线性函数
反平方根线性函数表达式:
f
(
x
)
=
{
x
1
+
α
x
2
,
x
<
0
x
,
x
≥
0
f(x)= \begin{cases} \begin{array}{ll}\frac{x}{\sqrt{1+\alpha x^2}},x<0\\x,x\ge 0 \end{array} \end{cases}
f(x)={1+αx2x,x<0x,x≥0
求导:
f
′
(
x
)
=
{
(
1
1
+
α
x
2
)
3
,
x
<
0
1
,
x
≥
0
f'(x)= \begin{cases} \begin{array}{ll}(\frac{1}{\sqrt{1+\alpha x^2}})^3,x<0\\1,x\ge 0 \end{array} \end{cases}
f′(x)={(1+αx21)3,x<01,x≥0

CeLU
C E L U ( x ) = m a x ( 0 , x ) + m i n ( 0 , α ∗ ( e x p ( x / a ) − 1 ) ) CELU(x)=max(0,x)+min(0,\alpha*(exp(x/a)-1)) CELU(x)=max(0,x)+min(0,α∗(exp(x/a)−1))
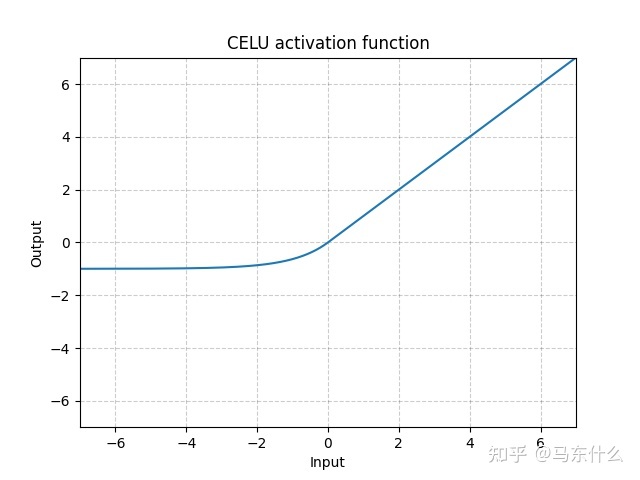
relu的复合型
Dynamic ReLU(2020)
Parper:[2003.10027] Dynamic ReLU (arxiv.org)
https://blog.csdn.net/qq_38253797/article/details/119007986
softplus
Softplus函数是Logistic-Sigmoid函数原函数:
S
o
f
t
p
l
u
s
(
x
)
=
l
n
(
1
+
e
x
)
Softplus(x)=ln(1+e^x)
Softplus(x)=ln(1+ex)
加了1是为了保证非负性。Softplus可以看做是ReLU函数的一个平滑版本。红色的即为ReLU。

Softplus 函数其导数刚好是Logistic 函数。Softplus 函数虽然也具有单侧抑制、宽兴奋边界的特性,却没有稀疏激活性。
求导:
S
o
f
t
p
l
u
s
′
(
x
)
=
e
x
1
+
e
x
Softplus'(x)=\frac{e^x}{1+e^x}
Softplus′(x)=1+exex
GLU函数+GTU函数
GLU、GTU 单元是基于Gate mechanism的,gate units有助于深度网络建模。
门控线性单元Gated linear units是在Language model with gated convolutional network中提出。
Tanh激活函数和GTU都存在梯度消失的问题,因为即使是GTU,当神经元的激活处于饱和区时,组成结构部分都会削弱梯度值。相反,GLU和Relu不存在这样的问题。GLU和Relu都拥有线性的通道,可以使梯度很容易通过激活的神经元,反向传播且不会减小。因此,采用GLU或Relu做为激活,训练时收敛速度更快
(1)GTU(Gated Tanh Unit)
表达式为: f ( X ) = t a n h ( X ∗ W + b ) ⊗ σ ( X ∗ V + c ) f(X) = tanh(X*W+b) \otimes \sigma(X*V+c) f(X)=tanh(X∗W+b)⊗σ(X∗V+c)
组成结构:Tanh激活单元: t a n h ( X ∗ W + b ) tanh(X*W+b) tanh(X∗W+b),加上一个Sigmoid激活单元: σ ( X ∗ V + c ) \sigma(X*V+c) σ(X∗V+c),构成的gate unit,就构成了GTU单元。
(2)GLU(Gated Liner Unit)
表达式为: f ( X ) = ( X ∗ W + b ) ⊗ σ ( X ∗ V + c ) f(X) = (X * W + b) \otimes \sigma(X * V + c) f(X)=(X∗W+b)⊗σ(X∗V+c)
组成结构:Relu激活单元: ( X ∗ W + b ) (X * W + b) (X∗W+b),加上一个Sigmoid激活单元: σ ( X ∗ V + c ) \sigma(X * V + c) σ(X∗V+c),构成的gate unit,就构成了GLU单元
首先我们可以通过堆叠CNN来标识长文本,提取更高层、更抽象的特征,而且相比LSTM而言,我们需要的op更少(CNN需要O(N/k)个op,而LSTM将文本视为序列需要O(N)个op,其中N为文本长度,k为卷积核宽度),这样一来,我们需要的非线性操作也更少,有效地降低了梯度弥散的现象,使模型收敛和训练变得更加简单。
此外,LSTM中模型下一时刻的输出依赖于前一个时刻的隐藏层状态,无法实现模型并行化。但是,CNN无需这种依赖,可以方便的实现并行化,从而实现计算速度的提升。最后,本文中提出的线性门控单元不仅有效地降低了梯度弥散,而且还保留了非线性的能力。
激活函数:Sigmoid,Tanh,Softmax,Swish,Relu系列,GLU+GTU
APL:自适应分段线性函数
f ( x ) = m a x ( 0 , x ) + ∑ s = 1 S a i s m a x ( 0 , − x + b i s ) f ′ ( x ) = H ( x ) − ∑ s = 1 S a i s H ( − x + b i s ) f(x)=max(0,x)+\sum_{s=1}^{S}a^s_{i}max(0,-x+b^s_i)\qquad\qquad f^{'}(x)=H(x)-\sum^{S}_{s=1}a^s_iH(-x+b^s_i) f(x)=max(0,x)+s=1∑Saismax(0,−x+bis)f′(x)=H(x)−s=1∑SaisH(−x+bis)
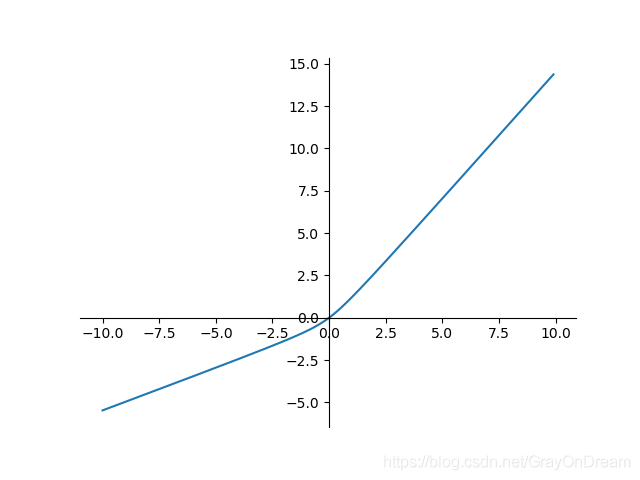
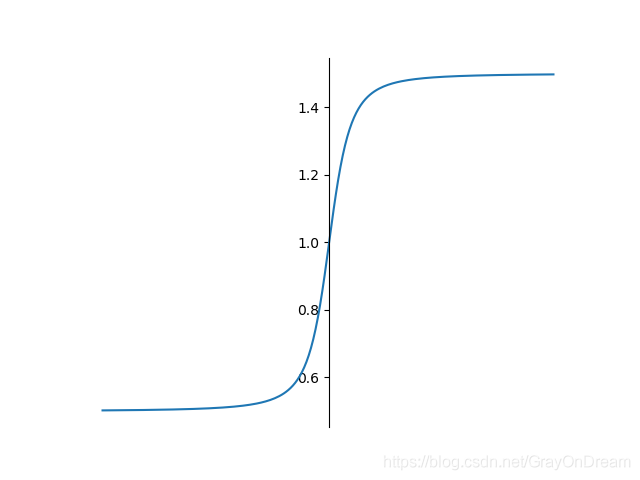
弯曲恒等函数
f ( x ) = x 2 + 1 − 1 2 + x f ′ ( x ) = x 2 x 2 + 1 + 1 f(x)=\frac{\sqrt{x^2+1}-1}{2}+x\qquad\qquad f^{'}(x)=\frac{x}{2\sqrt{x^2+1}}+1 f(x)=2x2+1−1+xf′(x)=2x2+1x+1
SoftExponential
函数表达式:
f
(
x
)
=
{
−
l
n
(
1
−
α
(
x
+
α
)
)
α
,
α
<
0
x
,
α
=
0
e
α
x
−
1
α
,
α
>
0
f(x)=\begin{cases}\begin{array} {ll} -\frac{ln(1-\alpha(x+\alpha))}{\alpha}, \alpha < 0\\ x,\alpha=0\\ \frac{e^{\alpha x}-1}{\alpha},\alpha >0 \end{array} \end{cases}
f(x)=⎩
⎨
⎧−αln(1−α(x+α)),α<0x,α=0αeαx−1,α>0
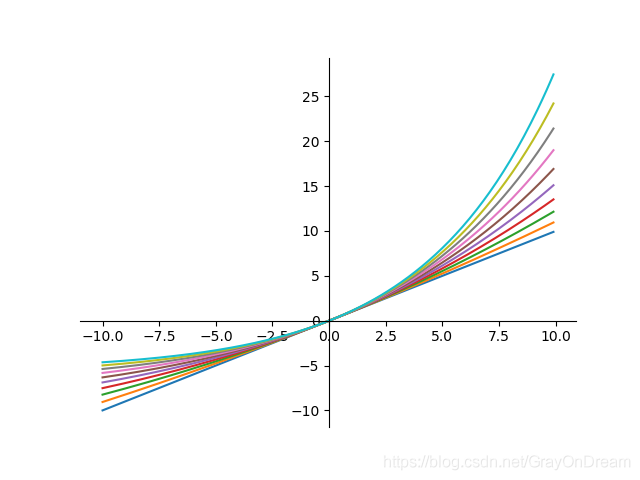
导数:
f
′
(
x
)
=
{
1
1
−
α
(
α
+
x
)
,
α
<
0
e
α
x
,
α
≥
0
f'(x)=\begin{cases} \begin{array} {ll} \frac{1}{1-\alpha(\alpha+x)},\alpha < 0\\ e^{\alpha x},\alpha \ge 0 \end{array} \end{cases}
f′(x)={1−α(α+x)1,α<0eαx,α≥0
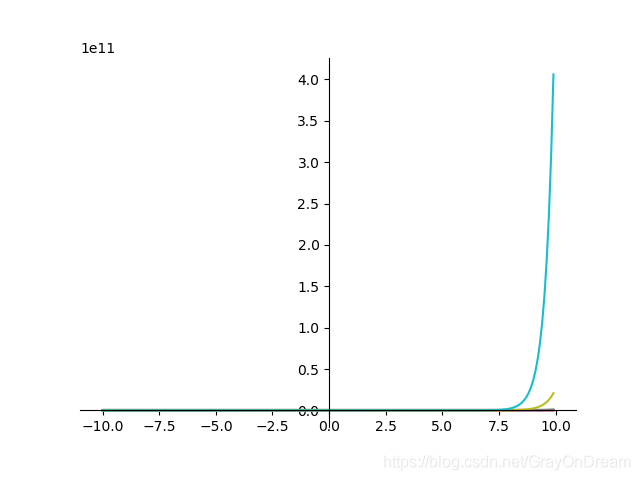
正弦函数
f ( x ) = s i n ( x ) f ′ ( x ) = c o s ( x ) f(x)= sin(x)\qquad\qquad f^{'}(x)=cos(x) f(x)=sin(x)f′(x)=cos(x)
Sinc函数
函数表达式:
f
(
x
)
=
{
1
,
x
=
0
s
i
n
(
x
)
x
,
x
≠
0
f(x)=\begin{cases}\begin{array} {ll} 1,x=0 \\ \frac{sin(x)}{x},x\ne 0 \end{array}\end{cases}
f(x)={1,x=0xsin(x),x=0
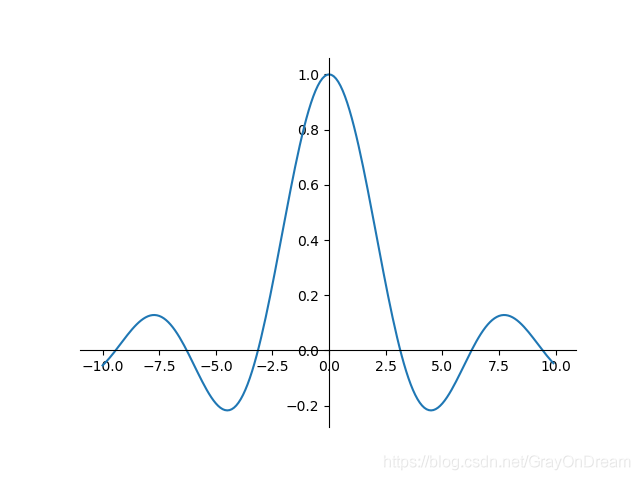
求导:
f
′
(
x
)
=
{
0
,
x
=
0
c
o
s
(
x
)
x
−
s
i
n
(
x
)
x
,
x
≠
0
f'(x)=\begin{cases}\begin{array} {ll} 0,x=0 \\ \frac{cos(x)}{x}-\frac{sin(x)}{x},x\ne 0 \end{array}\end{cases}
f′(x)={0,x=0xcos(x)−xsin(x),x=0
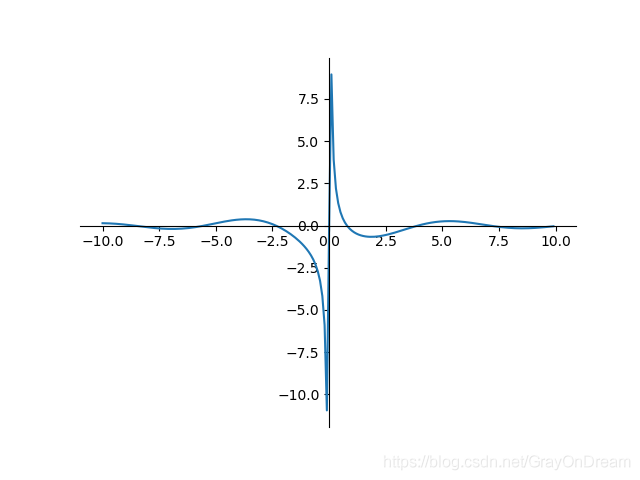
高斯函数
f ( x ) = e − x 2 f ′ ( x ) = − 2 x e − x 2 f(x)=e^{-x^2} \qquad\qquad f^{'}(x)=-2xe^{-x^2} f(x)=e−x2f′(x)=−2xe−x2
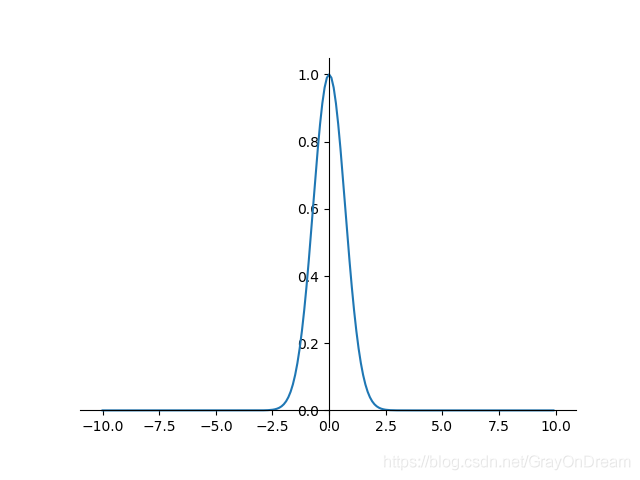
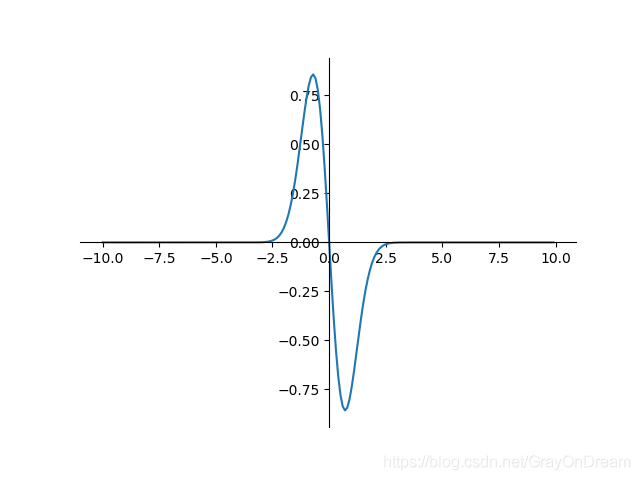
ACON:(Activate Or Not)激活函数
Activate or Not: Learning Customized Activation
CVPR 2021 | 自适应激活函数ACON: 统一ReLU和Swish的新范式
本文进一步分析ReLU的一般形式Maxout系列激活函数,从而得到Swish的一般形式、简单且有效的ACON激活函数。
Swish
paper : Searching for Activation Functions(Prajit Ramachandran,Google Brain 2017)
SEARCHING FOR ACTIVATION FUNCTIONS翻译
函数式:
s
w
i
s
h
(
x
)
=
x
⋅
s
i
g
m
o
i
d
(
β
x
)
swish(x) = x \cdot sigmoid(\beta x)
swish(x)=x⋅sigmoid(βx)
β
\beta
β是个常数或可训练的参数,Swish 具备无上界有下界、平滑、非单调的特性。
当 β \beta β = 0时,Swish变为线性函数 f ( x ) = x 2 f(x)= {x \over 2} f(x)=2x
$\beta → \infty,\sigma(x)=(1+e{−x}){−1} $为0或1,Swish变为ReLU: f ( x ) = 2 m a x ( 0 , x ) f(x)=2max(0,x) f(x)=2max(0,x)
所以Swish函数可以看做是介于线性函数与ReLU函数之间的平滑函数。
Swish 在深层模型上的效果优于 ReLU。例如,仅仅使用 Swish 单元替换 ReLU 就能把 Mobile NASNetA 在 ImageNet 上的 top-1 分类准确率提高 0.9%,Inception-ResNet-v 的分类准确率提高 0.6%。
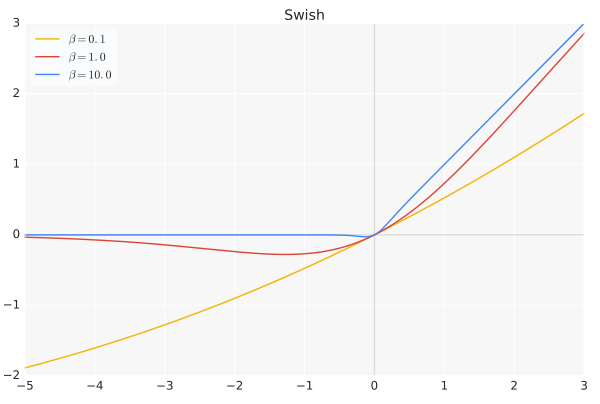
求导推导:
s
w
i
s
h
(
x
)
=
x
∗
(
1
+
e
−
x
)
−
1
s
w
i
s
h
′
(
x
)
=
x
′
∗
(
1
+
e
−
x
)
−
1
+
[
(
1
+
e
−
x
)
−
1
]
′
∗
x
=
1
∗
(
1
+
e
−
x
)
−
1
+
x
∗
[
−
(
1
+
e
−
x
)
−
2
∗
(
−
e
−
x
)
]
=
1
1
+
e
−
x
+
x
∗
e
−
x
(
1
+
e
−
x
)
2
=
1
1
+
e
−
x
+
x
∗
(
1
+
e
−
x
(
1
+
e
−
x
)
2
−
1
(
1
+
e
−
x
)
2
)
=
1
1
+
e
−
x
+
x
1
+
e
−
x
−
x
(
1
+
e
−
x
)
2
=
s
i
g
m
o
i
d
(
x
)
+
x
∗
s
i
g
m
o
i
d
(
x
)
−
x
∗
s
i
g
m
o
i
d
(
x
)
2
=
x
∗
s
i
g
m
o
i
d
(
x
)
+
s
i
g
m
o
i
d
(
x
)
(
1
−
x
⋅
s
i
g
m
o
i
d
(
x
)
)
=
s
w
i
s
h
(
x
)
+
s
i
g
m
o
i
d
(
x
)
(
1
−
s
w
i
s
h
(
x
)
)
\begin{equation} \begin{aligned} swish(x) &= x * (1 + e^{-x})^{-1}\\ swish'(x) &=x' * (1+e^{-x})^{-1}+ [(1+e^{-x})^{-1}]'*x \\ &= 1 * (1+e^{-x})^{-1}+ x * [-(1+e^{-x})^{-2} * (- e^{-x})] \\ &= \frac{1}{1+e^{-x}}+ x * \frac{e^{-x}}{(1+e^{-x})^2} \\ &= \frac{1}{1+e^{-x}}+ x * (\frac{1+e^{-x}}{(1+e^{-x})^2} - \frac{1}{(1+e^{-x})^2}) \\ &= \frac{1}{1+e^{-x}}+ \frac{x}{1+e^{-x}} - \frac{x}{(1+e^{-x})^2} \\ &= sigmoid(x)+ x * sigmoid(x) - x * sigmoid(x)^2 \\ &= x * sigmoid(x)+ sigmoid(x)(1- x \cdot sigmoid(x)) \\ &= swish(x)+ sigmoid(x)(1-swish(x)) \end{aligned} \end{equation}
swish(x)swish′(x)=x∗(1+e−x)−1=x′∗(1+e−x)−1+[(1+e−x)−1]′∗x=1∗(1+e−x)−1+x∗[−(1+e−x)−2∗(−e−x)]=1+e−x1+x∗(1+e−x)2e−x=1+e−x1+x∗((1+e−x)21+e−x−(1+e−x)21)=1+e−x1+1+e−xx−(1+e−x)2x=sigmoid(x)+x∗sigmoid(x)−x∗sigmoid(x)2=x∗sigmoid(x)+sigmoid(x)(1−x⋅sigmoid(x))=swish(x)+sigmoid(x)(1−swish(x))
导数:
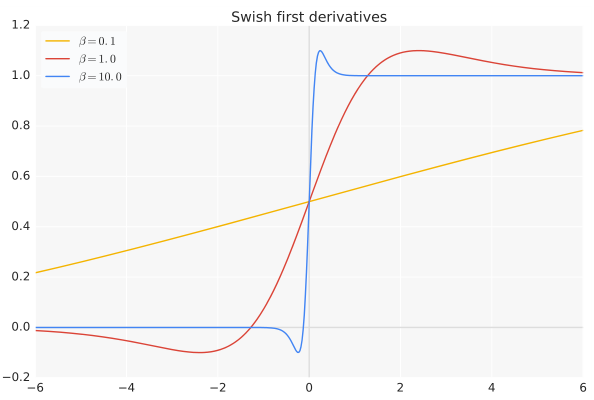
当
β
=
0
\beta=0
β=0 时,Swish变为线性函数
f
(
x
)
=
x
2
f(x) ={x\over 2}
f(x)=2x.
β
→
∞
\beta \to \infty
β→∞,
σ
(
x
)
=
(
1
+
exp
(
−
x
)
)
−
1
σ(x) = (1 + \exp(−x))^{−1}
σ(x)=(1+exp(−x))−1为0或1。 Swish变为ReLU:
f
(
x
)
=
2
m
a
x
(
0
,
x
)
f(x)=2max(0,x)
f(x)=2max(0,x)
所以Swish函数可以看做是介于线性函数与ReLU函数之间的平滑函数。
工程实现:
在TensorFlow框架中只需一行代码: x * tf.sigmoid(beta * x)或tf.nn.swish(x).
在Caffe中使用Scale+Sigmoid+EltWise(PROD)来实现或者合并成一个层。 代码参考.
Maxout
论文 Maxout Networks(Goodfellow,ICML2013)
Maxout 可以看做是在深度学习网络中加入一层激活函数层, 包含一个参数 k。 这一层相比 ReLU,sigmoid 等, 其特殊之处在于增加了 k 个神经元, 然后输出激活值最大的值。
我们常见的隐含层节点输出:
h
i
(
x
)
=
sigmoid
(
x
T
W
…
i
+
b
i
)
h_i(x)=\text{sigmoid}(x^TW_{…i}+b_i)
hi(x)=sigmoid(xTW…i+bi)
而在Maxout网络中,其隐含层节点的输出表达式为:
h
i
(
x
)
=
max
j
∈
[
1
,
k
]
z
i
j
h_i(x)=\max_{j\in[1,k]}z_{ij}
hi(x)=j∈[1,k]maxzij
其中
z
i
j
=
x
T
W
…
i
j
+
b
i
j
,
W
∈
R
d
×
m
×
k
z_{ij}=x^TW_{…ij}+b_{ij}, W\in R^{d\times m\times k}
zij=xTW…ij+bij,W∈Rd×m×k
假设网络第i层有2个神经元x1、x2,第i+1层的神经元个数为1个。原本只有一层参数,将ReLU或sigmoid等激活函数替换掉,引入Maxout,将变成两层参数,参数个数增为k倍。
特点:
- Maxout的拟合能力非常强,可以拟合任意的凸函数。
- Maxout具有ReLU的所有优点,线性、不饱和性。
- 同时没有ReLU的一些缺点。如:神经元的死亡
- maxout激活函数并不是一个固定的函数,不像Sigmod、Relu、Tanh等函数,是一个固定的函数方程
- 它是一个可学习的激活函数,因为我们W参数是学习变化的。
- 它是一个分段线性函数:
缺点:
从上面的激活函数公式中可以看出,每个神经元中有两组(w,b)参数,那么参数量就增加了一倍,这就导致了整体参数的数量激增。与常规激活函数不同的是,它是一个可学习的分段线性函数。
然而任何一个凸函数,都可以由线性分段函数进行逼近近似。其实我们可以把以前所学到的激活函数:ReLU、abs激活函数,看成是分成两段的线性函数,如下示意图所示:
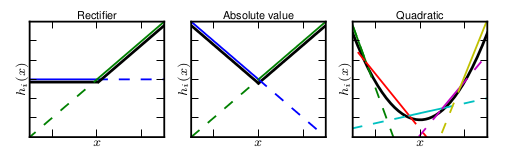
maxout的拟合能力是非常强的,它可以拟合任意的的凸函数。最直观的解释就是任意的凸函数都可以由分段线性函数以任意精度拟合(学过高等数学应该能明白),而maxout又是取k个隐隐含层节点的最大值,这些”隐隐含层"节点也是线性的,所以在不同的取值范围下,最大值也可以看做是分段线性的(分段的个数与k值有关)。
maxout是一个函数逼近器**,**对于一个标准的MLP网络来说,如果隐藏层的神经元足够多,那么理论上我们是可以逼近任意的函数的。类似的,对于maxout 网络也是一个函数逼近器。
实验结果表明Maxout与Dropout组合使用可以发挥比较好的效果。
那么,前边的两种ReLU便是两种Maxout,函数图像为两条直线的拼接, f ( x ) = max ( w 1 T x + b 1 , w 2 T x + b 2 ) f(x)=\max(w_1^Tx+b_1,w_2^Tx+b_2) f(x)=max(w1Tx+b1,w2Tx+b2)
hard-Swish
paper : Searching for MobileNetV3
函数式:
h
-
s
w
i
s
h
[
x
]
=
x
R
e
L
U
6
(
x
+
3
)
6
h\text{-}swish[x] = x \frac{ReLU6(x+3)}{6}
h-swish[x]=x6ReLU6(x+3)
求导推导:
h
-
s
w
i
s
h
′
(
x
)
=
R
e
L
U
6
(
x
+
3
)
6
+
x
6
∗
R
e
L
U
6
′
(
x
+
3
)
=
{
1
if
x
>
3
x
+
3
6
+
x
6
if
−
3
≤
x
≤
3
0
if
x
<
−
3
\begin{equation} \begin{aligned} h\text{-}swish'(x) &= \frac{ReLU6(x+3)}{6} + \frac{x}{6} * ReLU6'(x+3) \\ &= \begin{cases} 1 &\text{if } x > 3 \\ \frac{x+3}{6} + \frac{x}{6} &\text{if } -3 \le x \le 3 \\ 0 &\text{if } x < -3 \\ \end{cases} \end{aligned} \end{equation}
h-swish′(x)=6ReLU6(x+3)+6x∗ReLU6′(x+3)=⎩
⎨
⎧16x+3+6x0if x>3if −3≤x≤3if x<−3
EliSH与HardEliSH
其他的研究人员通过遗传算法学习到一些新的激活函数The Quest for the Golden Activation Function
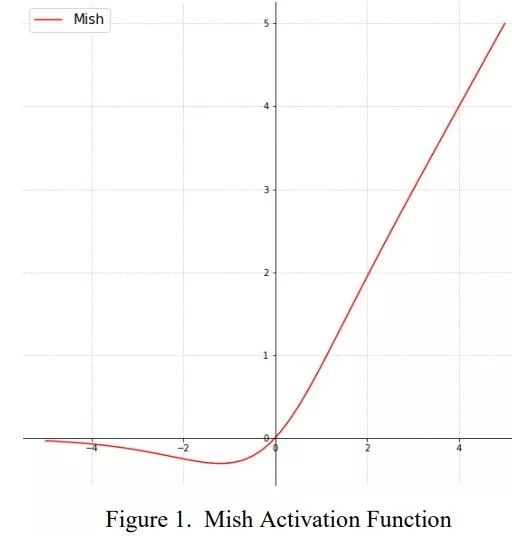
Mish
paper : Mish: A self Regularized Non-Monotonic Neural Activation Function论文介绍了一个新的深度学习激活函数,该函数在最终准确度上比Swish(+.494%)和ReLU(+ 1.671%)都有提高。
使用Mish代替ReLU,打破了之前在FastAI全球排行榜上准确性得分记录的一部分。结合Ranger优化器,Mish激活,Flat + Cosine 退火和自注意力层,能够获得12个新的排行榜记录。
函数式:
M
i
s
h
(
x
)
=
x
⋅
tanh
(
ln
(
1
+
e
x
)
)
Mish(x) = x \cdot \tanh{(\ln{(1+e^x)})}
Mish(x)=x⋅tanh(ln(1+ex))
ReLU和Mish的对比,Mish的梯度更平滑
Mish的PyTorch实现,用它替换了ReLU,没有做任何其他更改,并在困难的ImageWoof数据集上使用广泛的优化器(Adam、Ranger、RangerLars、Novograd等)对它进行了测试。Mish在训练稳定性、平均准确率(1-2.8%)、峰值准确率(1.2% - 3.6%)等方面都有了全面的提高,与本文的结果相匹配或超过。
1.无上界有下界:无上界是任何激活函数都需要的特征,因为它避免了导致训练速度急剧下降的梯度饱和,因此加快训练过程。无下界有助于实现强正则化效果(适当的拟合模型)。(这个性质类似于ReLU和 Swish 的性质,其范围是 [ ≈ 0.31 , ∞ ] ) [\approx 0.31,\infty]) [≈0.31,∞])
2.非单调函数:这种性质有助于保持小的负值,从而稳定网络梯度流。大多数常用的激活函数,如ReLU [$ f(x)= max(0, x)$],Leaky ReLU[ f ( x ) = m a x ( 0 , x ) , 1 f(x) = max (0, x),1 f(x)=max(0,x),1 ],由于其差分为0,不能保持负值,因此大多数神经元没有得到更新。
3.无穷阶连续性和光滑性:Mish函数是光滑函数,具有较好的泛化能力和结果的有效优化能力,可以提高结果的质量。
求导推导:
tanh
(
x
)
=
e
x
−
e
−
x
e
x
+
e
−
x
=
e
2
x
−
1
e
2
x
+
1
M
=
ln
(
1
+
e
x
)
→
e
M
=
1
+
e
x
tanh
(
ln
(
1
+
e
x
)
)
=
tanh
(
M
)
=
e
2
M
−
1
e
2
M
+
1
=
(
1
+
e
x
)
2
−
1
(
1
+
e
x
)
2
+
1
M
i
s
h
(
x
)
=
x
∗
(
1
+
e
x
)
2
−
1
(
1
+
e
x
)
2
+
1
f
=
1
+
e
x
→
M
i
s
h
(
x
)
=
x
∗
f
2
−
1
f
2
+
1
M
i
s
h
′
(
x
)
=
f
2
−
1
f
2
+
1
+
x
∗
(
f
2
−
1
f
2
+
1
)
′
(
f
2
−
1
f
2
+
1
)
′
=
(
f
2
−
1
)
′
(
f
2
+
1
)
−
(
f
2
+
1
)
′
(
f
2
−
1
)
(
f
2
+
1
)
2
(
f
2
−
1
)
′
=
2
e
2
x
+
2
e
x
=
(
f
2
+
1
)
′
⇓
M
i
s
h
′
(
x
)
=
4
f
(
f
−
1
)
(
f
2
+
1
)
2
∗
x
+
f
2
−
1
f
2
+
1
\begin{equation} \begin{aligned} \tanh{(x)} &= \frac{e^x-e^{-x}}{e^x+e^{-x}} \\ &= \frac{e^{2x}-1}{e^{2x}+1} \\ \\ M &= \ln{(1+e^x)} \rightarrow e^M = 1+e^x \\ \\ \tanh{(\ln{(1+e^x)})} &= \tanh{(M)} \\ &= \frac{e^{2M}-1}{e^{2M}+1} \\ &= \frac{(1+e^x)^2-1}{(1+e^x)^2 + 1} \\ \\ Mish(x) &= x * \frac{(1+e^x)^2-1}{(1+e^x)^2 + 1} \\ f&= 1+e^x \rightarrow Mish(x) = x * \frac{f^2-1}{f^2+1} \\ Mish'(x) &= \frac{f^2-1}{f^2+1} + x*(\frac{f^2-1}{f^2+1})' \\ (\frac{f^2-1}{f^2+1})' &= \frac{(f^2-1)'(f^2+1) - (f^2+1)'(f^2-1)}{(f^2+1)^2} \\ (f^2-1)' &= 2e^{2x}+ 2e^x =(f^2+1)' \\ \Downarrow \\ Mish'(x) &= \frac{4f(f-1)}{(f^2+1)^2}*x + \frac{f^2-1}{f^2+1} \end{aligned} \end{equation}
tanh(x)Mtanh(ln(1+ex))Mish(x)fMish′(x)(f2+1f2−1)′(f2−1)′⇓Mish′(x)=ex+e−xex−e−x=e2x+1e2x−1=ln(1+ex)→eM=1+ex=tanh(M)=e2M+1e2M−1=(1+ex)2+1(1+ex)2−1=x∗(1+ex)2+1(1+ex)2−1=1+ex→Mish(x)=x∗f2+1f2−1=f2+1f2−1+x∗(f2+1f2−1)′=(f2+1)2(f2−1)′(f2+1)−(f2+1)′(f2−1)=2e2x+2ex=(f2+1)′=(f2+1)24f(f−1)∗x+f2+1f2−1
Mish:一个新的state-of-the-art激活函数,ReLU的继任者
Mish: A Self Regularized Non-Monotonic Activation Function 论文笔记
可以参考:https://zhuanlan.zhihu.com/p/84418420
Softmax
函数式:
p
i
=
e
a
i
∑
k
=
1
N
e
a
k
p_i = \frac{e^{a_i}}{\sum_{k=1}^N e^{a_k}}
pi=∑k=1Neakeai
求导推导:
∂
p
j
∂
a
j
=
{
p
i
(
1
−
p
j
)
if
i
=
j
−
p
j
⋅
p
i
if
i
≠
j
\frac{\partial p_j}{\partial a_j} = \begin{cases} p_i(1-p_j) &\text{if } i=j \\ -p_j \cdot p_i &\text{if } i \ne j \end{cases}
∂aj∂pj={pi(1−pj)−pj⋅piif i=jif i=j
sparsemax
sparsemax是2016年提出的。softmax缺点:每个向量位置都有值。文章From Softmax to Sparsemax:A Sparse Model of Attention and Multi-Label Classification 提出了能够输出稀疏概率的Sparsemax。
这里把输入 z 和某个分布 p 的欧式距离最小化。
一种具体的实现是,
shrink系列
SoftShrink
S o f t S h r i n k ( x ) = { x − λ , x > λ x + λ , x < − λ 0 , o t h e r w i s e \begin{equation} SoftShrink(x)= \begin{cases} x-\lambda, & \text{$x \gt \lambda$} \\ x+\lambda, & \text{$x< - \lambda$} \\0, & \text{$otherwise$} \end{cases} \end{equation} SoftShrink(x)=⎩ ⎨ ⎧x−λ,x+λ,0,x>λx<−λotherwise
HardShrink
H a r d S h r i n k ( x ) = { x , x > λ x , x < − λ 0 , o t h e r w i s e \begin{equation} HardShrink(x)= \begin{cases} x, & \text{$x \gt \lambda$} \\ x, & \text{$x< - \lambda$} \\0, & \text{$otherwise$} \end{cases} \end{equation} HardShrink(x)=⎩ ⎨ ⎧x,x,0,x>λx<−λotherwise
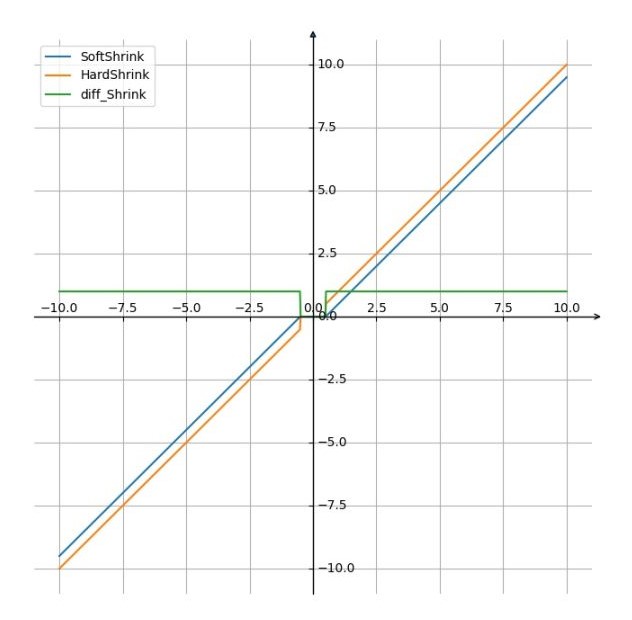
0点处做平滑处理。
TanhShrink
T a n h S h r i n k ( x ) = x − t a n h ( x ) = x − e x − e − x e x + e − x TanhShrink(x)=x-tanh(x)=x- \frac{e^x - e^{-x}}{e^x+e^{-x}} TanhShrink(x)=x−tanh(x)=x−ex+e−xex−e−x
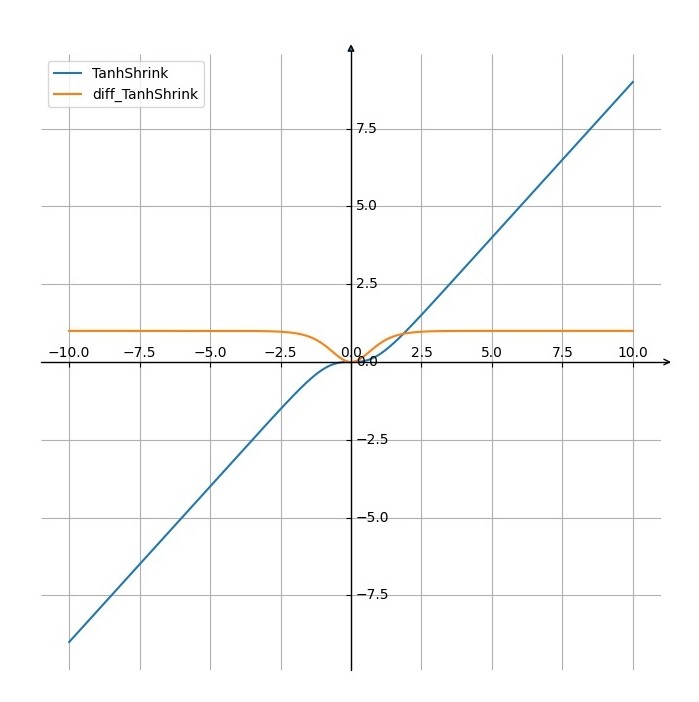
hard系列:
hard系列基本上都是对原始的函数进行取值限制从而 进一步转化为分段线性函数
hardtanh
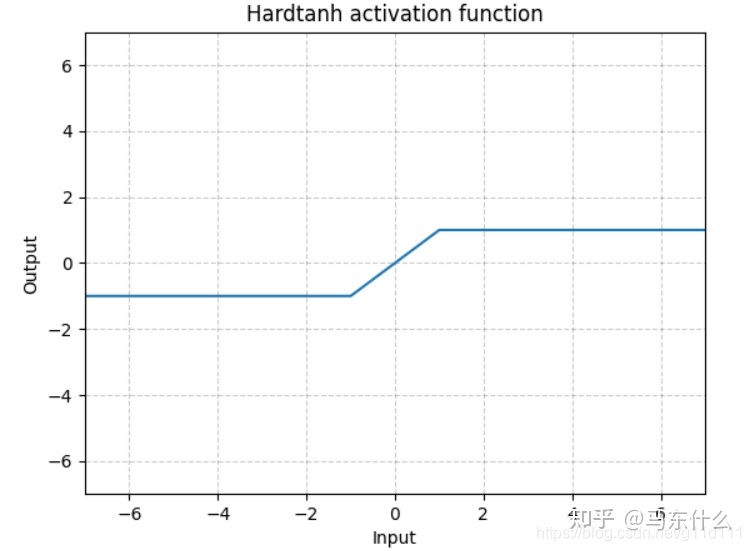
H a r d T a n h ( x ) = { 1 , x > 1 − 1 , x < − 1 x , o t h e r w i s e \begin{equation} HardTanh(x)= \begin{cases} 1, & \text{$x \gt 1$} \\ -1, & \text{$x< - 1$} \\x, & \text{$otherwise$} \end{cases} \end{equation} HardTanh(x)=⎩ ⎨ ⎧1,−1,x,x>1x<−1otherwise
hardswish
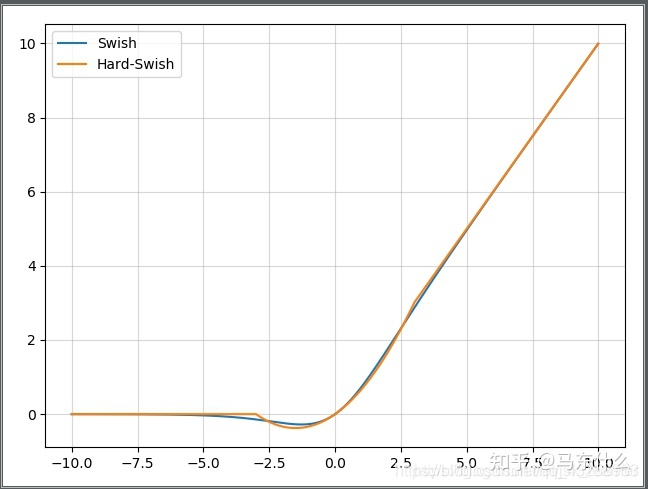
h a r d s w i s h ( x ) = x R e L U 6 ( x + 3 ) 6 hardswish(x)=x \frac{ReLU6(x+3)}{6} hardswish(x)=x6ReLU6(x+3)
Relu6(hard sigmoid)
R e L U 6 = m i n ( 6 , m a x ( 0 , x ) ) ReLU6=min(6,max(0,x)) ReLU6=min(6,max(0,x))
(对于hard的activation而言,主要目的就两个,一个是稀疏学习,一个是降低计算成本节约精度存储)
激活函数的作用
- 加入非线性因素
- 充分组合特征
下面说明一下为什么有组合特征的作用。
一般函数都可以通过泰勒展开式来近似计算, 如sigmoid激活函数中的指数项可以通过如下的泰勒展开来近似计算:
e
z
=
1
+
1
1
!
z
+
1
2
!
z
2
+
1
3
!
z
3
+
o
(
z
3
)
e^z=1+{1\over 1!}z+{1\over 2!}z^2+{1\over 3!}z^3+o(z^3)
ez=1+1!1z+2!1z2+3!1z3+o(z3)
其中有平方项,立方项及更更高项, 而
z
=
w
x
+
b
z=wx+b
z=wx+b, 因此可以看作是输入特征 $x $的组合。 以前需要由领域专家知识进行特征组合,现在激活函数能起到一种类似特征组合的作用。 (思想来源: 微博@算法组)
**为什么ReLU,Maxout等能够提供网络的非线性建模能力?**它们看起来是分段线性函数,然而并不满足完整的线性要求:加法 f ( x + y ) = f ( x ) + f ( y ) f(x+y)=f(x)+f(y) f(x+y)=f(x)+f(y)和乘法 f ( a x ) = a × f ( x ) f(ax)=a×f(x) f(ax)=a×f(x)或者写作 f ( α x 1 + β x 2 ) = α f ( x 1 ) + β f ( x 2 ) f(\alpha x_1+\beta x_2)=\alpha f(x_1)+\beta f(x_2) f(αx1+βx2)=αf(x1)+βf(x2)。非线性意味着得到的输出不可能由输入的线性组合重新得到(重现)。假如网络中不使用非线性激活函数,那么这个网络可以被一个单层感知器代替得到相同的输出,因为线性层加起来后还是线性的,可以被另一个线性函数替代。
梯度消失与梯度爆炸
梯度消失/爆炸原因及解决办法
原因,浅层的梯度计算需要后面各层的权重及激活函数导数的乘积,因此可能出现前层比后层的学习率小(vanishing gradient)或大(exploding)的问题,所以具有不稳定性。那么如何解决呢?
需要考虑几个方面:
- 权重初始化
使用合适的方式初始化权重, 如ReLU使用MSRA的初始化方式, tanh使用xavier初始化方式。 - 激活函数选择
激活函数要选择ReLU等梯度累乘稳定的。 - 学习率
一种训练优化方式是对输入做白化操作(包括正规化和去相关), 目的是可以选择更大的学习率。 现代深度学习网络中常使用Batch Normalization(包括正规化步骤,但不含去相关)。 (All you need is a good init. If you can’t find the good init, use Batch Normalization.)
由于梯度的公式包含每层激励的导数以及权重的乘积,因此让中间层的乘积约等于1即可。但是sigmoid这种函数的导数值又与权重有关系(最大值1/4,两边对称下降),所以含有sigmoid的神经网络不容易解决,输出层的activation大部分饱和,因此不建议使用sigmoid。
ReLU在自变量大于0时导数为1,小于0时导数为0,因此可以解决上述问题。
梯度爆炸
由于sigmoid,ReLU等函数的梯度都在[0,1]以内,所以不会引发梯度爆炸问题。 而梯度爆炸需要采用梯度裁剪、BN、设置较小学习率等方式解决。
激活函数选择
- 首先尝试ReLU,速度快,但要注意训练的状态。
- 如果ReLU效果欠佳,尝试Leaky ReLU或Maxout等变种。
- 尝试tanh正切函数(以零点为中心,零点处梯度为1)
- sigmoid/tanh在RNN(LSTM、注意力机制等)结构中有所应用,作为门控或者概率值。
- 在浅层神经网络中,如不超过4层的,可选择使用多种激励函数,没有太大的影响。
- https://en.wikipedia.org/wiki/Rectifier_(neural_networks) ↩︎
- https://zh.wikipedia.org/wiki/双曲函数 ↩︎
- http://mathforum.org/library/drmath/view/54179.html ↩︎
- 谈谈激活函数以零为中心的问题 https://liam0205.me/2018/04/17/zero-centered-active-function/ ↩︎
总结
神经网络中激活函数的真正意义?一个激活函数需要具有哪些必要的属性?还有哪些属性是好的属性但不必要的?
激活函数实现非线性?
从最原始理论里激活函数是阶跃函数,激活函数就是模拟神经元的激活状态和非激活状态。后来实际中因为需要优化,需要求导,才采用sigmoid这些变种的激活函数。
如果仅仅是为了实现非线性,是什么样的激活函数才是好的激活函数呢?激活函数的真正意义是什么?一个激活函数需要具有哪些必要的属性?还有哪些属性是好的属性但不必要的?
【AI初识境】激活函数:从人工设计(sigmoid,relu)到自动搜索(swish)
谷歌开了许多深度学习领域的自动化的工作,比如自动设计网络NASNet,自动数据增强AutoAugment等工作,也做了自动搜索最优的激活函数的工作。
论文Searching for activation functions就在一系列一元函数和二元函数组成的搜索空间中,进行了比较细致的组合搜索实验。
结论是好用的激活函数都比较简单,不会超过两个基本函数的乘的组合。搜到了一些比Relu表现更好的函数,最好的是一个这样的函数: x ⋅ σ ( β x ) x · \sigma(\beta x) x⋅σ(βx),被称为Swish,它在某个特定的参数下也和ReLU及其变种类似。
激活函数属性:
reference
- 激活函数(ReLU, Swish, Maxout)
- 有哪些好用的激活函数?
- 常见的激活函数Relu,Gelu,Mish,Swish,Tanh,Sigmoid
- 深度学习笔记:如何理解激活函数?(附常用激活函数)
- 网页urldecode解码
- 深度学习——激活函数(Sigmoid、Tanh、ReLU、Leaky-ReLU、ReLU6、Swish、Hard-Swish、Mish、Softmax)
- 常见和不常见激活函数整理
- 钒鑫学长CSDN
- 伯努利分布、二项分布、多项分布、Beta分布、Dirichlet分布
- 激活函数综述
- 23种激活函数
- 代码: 激活函数/损失函数汇总
- 深度学习的激活函数 :sigmoid、tanh、ReLU 、Leaky Relu、RReLU、softsign 、softplus、GELU
- 深度学习中的一些常见的激活函数集合(含公式与导数的推导)sigmoid, relu, leaky relu, elu, numpy实现
- 神经网络的激活函数总结
- 神经网络中激活函数的真正意义?一个激活函数需要具有哪些必要的属性?还有哪些属性是好的属性但不必要的?
- 神经网络梯度消失与梯度爆炸
常见激活函数整理](https://zhuanlan.zhihu.com/p/92412922)
8. 钒鑫学长CSDN
9. 伯努利分布、二项分布、多项分布、Beta分布、Dirichlet分布
10. 激活函数综述
11. 23种激活函数
12. 代码: 激活函数/损失函数汇总
13. 深度学习的激活函数 :sigmoid、tanh、ReLU 、Leaky Relu、RReLU、softsign 、softplus、GELU
14. 深度学习中的一些常见的激活函数集合(含公式与导数的推导)sigmoid, relu, leaky relu, elu, numpy实现
15. 神经网络的激活函数总结
16. 神经网络中激活函数的真正意义?一个激活函数需要具有哪些必要的属性?还有哪些属性是好的属性但不必要的?
17. 神经网络梯度消失与梯度爆炸

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








