DTW（Dynamic Time Warping）动态时间规整算法详解

最新推荐文章于 2025-03-12 16:18:39 发布

Lllongroad

最新推荐文章于 2025-03-12 16:18:39 发布

阅读量3.6k

点赞数 12

文章标签：算法

本文链接：https://blog.csdn.net/Lllongroad/article/details/143067618

版权

1.概念解释及应用

按照该论文中的解释，动态时间规整（Dynamic Time Warping, DTW）算法基于动态规划的解决问题方法，用于测量两个序列之间的相似性，这些序列在时间或空间上可能有所不同。相似性的衡量是通过计算两个时间序列之间的距离来实现的。因此该算法可以运用于诸如语音识别、手写字符识别，姿态识别等方面

2.DTW实现关键技术点

1）模板函数：根据前面的关于DTW算法的概念（计算两个序列的相似度），因此是需要制作要识别的声音、动作等的模板函数，一般来说，数据点不宜过多，因为不排除会有噪声点之类的，所以需要先对所收集的曲线进行去噪处理（这里我使用的是卡尔曼滤波），然后提取相应的特征点。如下图，主要是对惯性传感器的某轴加速度进行模板提取用于姿态识别。

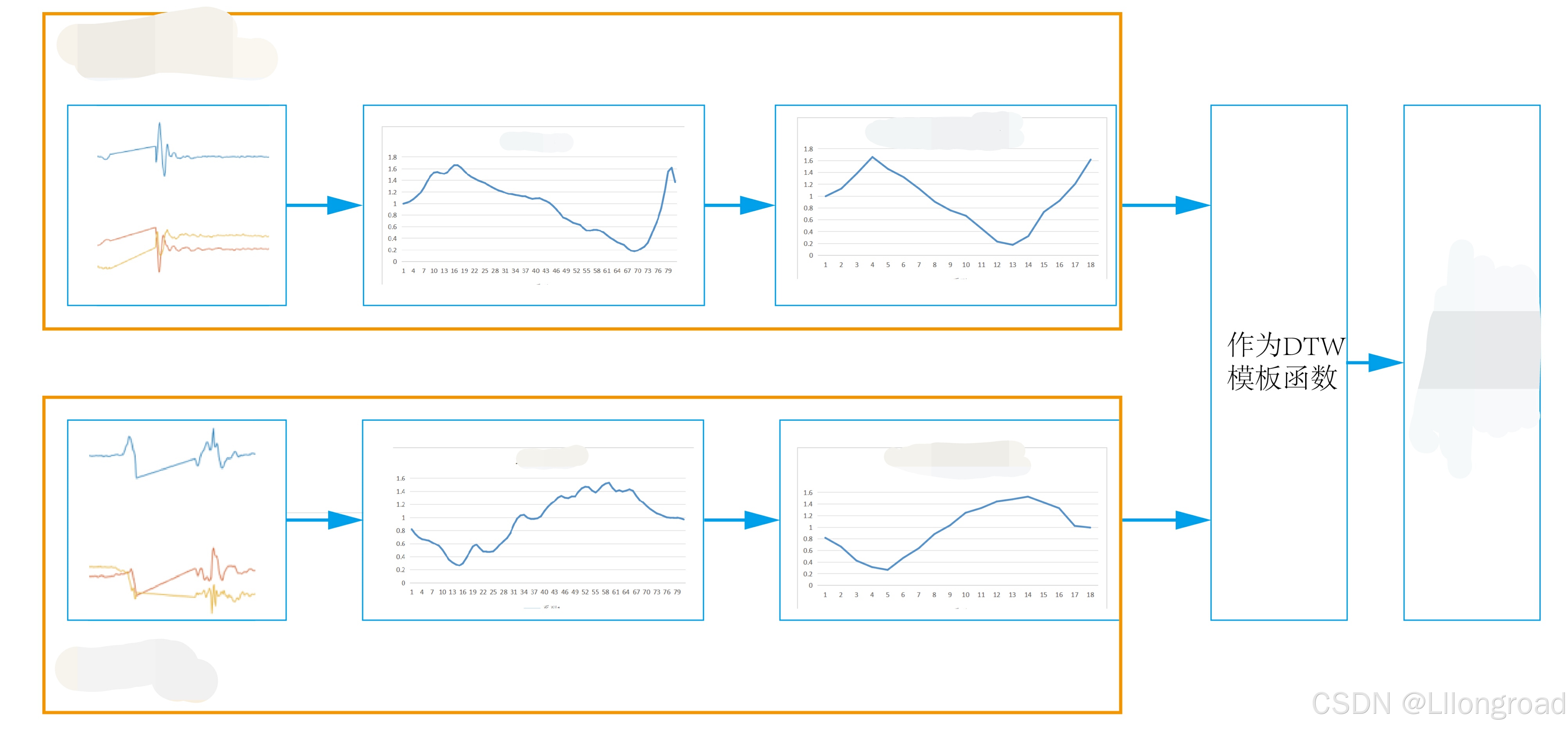
2）时间序列对齐：两段时间序列在某些情况下可能长度不同或在时间上有不一致的变化。例如，两个相似的动作，一个做得快，一个做得慢，DTW 通过拉伸或压缩时间轴，使它们尽可能对齐。

3）距离度量：DTW 通过计算两个时间序列中对应点的欧氏距离，来衡量它们的相似度。为了找到最佳匹配，DTW 会允许序列中的点重复使用，以最小化整体距离。

4）递归计算最优路径：DTW 使用动态规划来计算两个时间序列之间的最优路径。它会逐步比较时间序列的每个数据点，记录每个点之间的累积距离，从而找到使累积距离最小的路径。

3.DTW的计算实现

首先要明确，DTW是为了解决非等长时间序列数据的相似性计算问题而提出来的。经过时间规整后，两条数据就可以得到下图所示的对应关系，可以看到两条数据在时间轴上并不一一对应。

假设有两个时间序列A,B，长度分别为m和n。

$A=a_1,a_2,...a_m$

$B=b_1,b_2,...b_m$

为了对齐两个序列，算法中构造了一个 $m\times n$ 的矩阵，矩阵的位置 $\left ( i,j \right )$ 用于存储点 $a_i$ 与点 $b_j$ 的距离，（通常距离为欧式距离，即 $d(i,j)=\sqrt{(a_i-b_j)^2}$ ）.DTW算法的目的就是从矩阵中找出一条从 $\left ( 1,1 \right )$ 到 $\left ( m,n \right )$ 开销最小的一条路径。下图阐明了DTW算法的思想。路径W是矩阵中的连续元素（下面会给出"连续"的解释），它给出了A和B的对应关系。