BP神经网络和遗传算法
算法用途
-
BP(back propagation)神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络,是应用最广泛的神经网络模型之一。
-
遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的模型。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。遗传算法已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。
实例分析
用经典鲍鱼数据集为例,最后Rings是需要预测的即鲍鱼的年龄,用性别(1:雄性,M;0:中性l ; -1:雌性,F)和一些体征如长度、高度、重量等进行预测。因变量是鲍鱼的年龄,有多个自变量。前面推文用线性回归预测过。BP神经网络也可以用来解决这个问题,此篇用BP神经网络来解决这个回归问题。
鲍鱼数据形式如下:
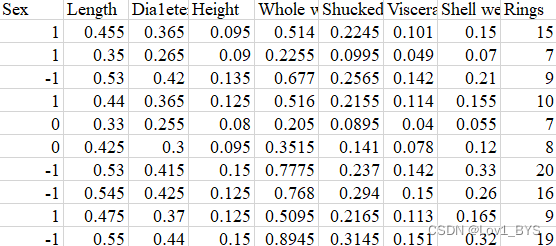
BP神经网络
首先来试下固定数据前80%为训练集和后20%为测试集,设置隐藏层神经元为6,激活函数为tansig时,随机运行10次BP神经网络的预测结果,记录其误差以及记录每次运行的时间
MATLAB自带神经网络求解:
clc;clear;close all;
load('abalone_data.mat')
[m,n]=size(data);
train_num=round(0.8*m); %前80%为训练集
x_train_data=data(1:train_num,1:n-1);
y_train_data=data(1:train_num,n);
x_test_data=data(train_num+1:end,1:n-1);
y_test_data=data(train_num+1:end,n);
x_train_data=x_train_data';
y_train_data=y_train_data';
x_test_data=x_test_data';
[x_train_regular,x_train_maxmin] = mapminmax(x_train_data);
[y_train_regular,y_train_maxmin] = mapminmax(y_train_data);
%创建网络
%%调用形式
EMS_all=[]; %运行误差记录
TIME=[]; %运行时间记录
num_iter_all=10; %随机运行次数
for NN=1:num_iter_all
t1=clock;
net=newff(x_train_regular,y_train_regular,6,{'tansig','purelin'});
[net,~]=train(net,x_train_regular,y_train_regular);
%将输入数据归一化
x_test_regular = mapminmax('apply',x_test_data,x_train_maxmin);
%放入到网络输出数据
y_test_regular=sim(net,x_test_regular);
%将得到的数据反归一化得到预测数据
BP_predict=mapminmax('reverse',y_test_regular,y_train_maxmin);
% RBF_predict(find(RBF_predict<0))=-0.244;
%%
BP_predict=BP_predict';
errors_nn=sum(abs(BP_predict-y_test_data)./(y_test_data))/length(y_test_data);
t2=clock;
Time_all=etime(t2,t1);
EMS_all=[EMS_all,errors_nn];
TIME=[TIME,Time_all];
end
figure(2)
% EMS_all=[0.151277426366310,0.145790071635758,0.152229836751767,0.147953564542518,0.143818740388519,0.143837148577291,0.150634730752498,0.147839770226974,0.148028820366280,0.145394520676572];
plot(EMS_all,'LineWidth',2)
xlabel('实验次数')
ylabel('误差')
hold on
figure(3)
color=[111,168,86;128,199,252;112,138,248;184,84,246]/255;
plot(y_test_data,'Color',color(2,:),'LineWidth',1)
hold on
plot(BP_predict,'*','Color',color(1,:))
hold on
titlestr=['MATLAB自带BP神经网络',' 误差为:',num2str(errors_nn)];
title(titlestr)
可以得到以下误差曲线,可见同样参数运行BP神经网络它的结果也可以相差比较大,主要是因为它的初始参数设置是随机的,因此就留给了优化的空间。
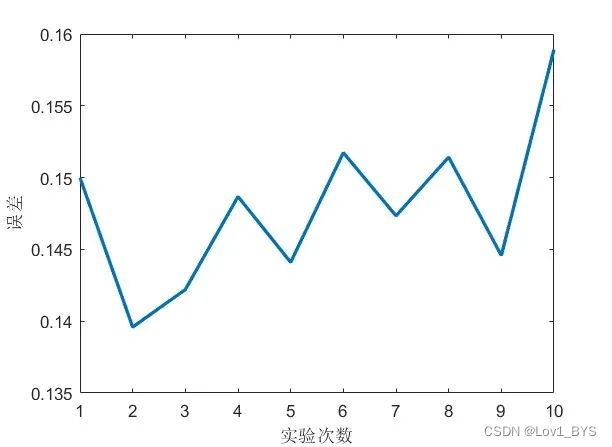
GA-BP神经网络
做优化要先明白优化的结果是什么?
- 使得网络参数配置最优,测试集预测误差最小——适应度函数
可以通过改变什么来使得网络结果不同?
- 可以改变网络参数的初始值,再用BP神经网络的反向传播来寻得整个网络参数的最优
- 可以直接遗传算法优化整个网络参数,不引进BP反向传播来获得最佳的网络参数设置
- 可以改变参数的初始值,用遗传算法在正向传播里优化出比较好的初始参数,再用反向传播优化参数
遗传算法的步骤:
1. 确定编码的方式
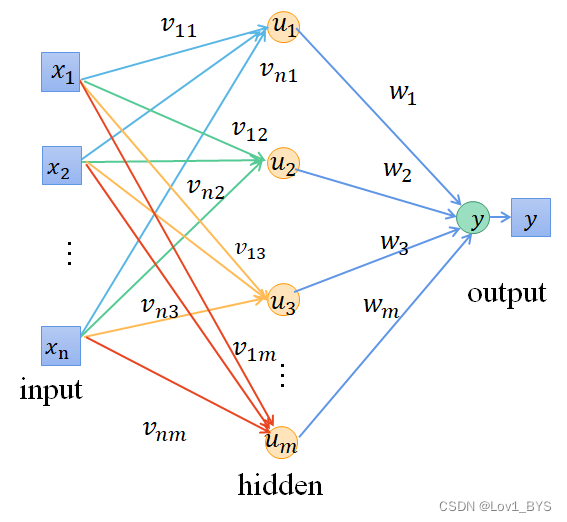
回顾一下BP神经网络的参数
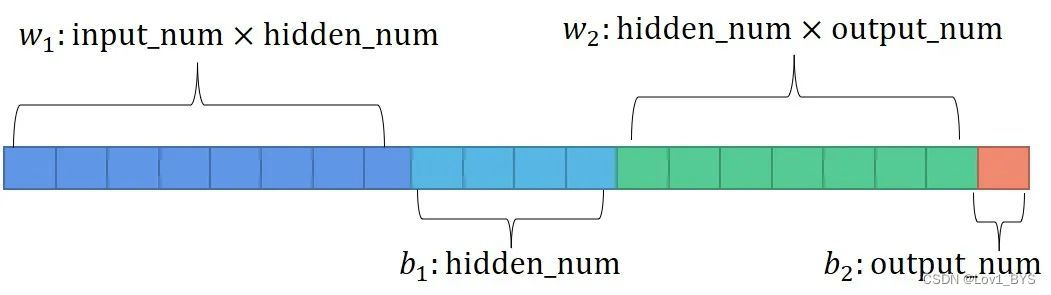
可以将所有参数平铺成一条染色体的形式
2. 产生初始种群
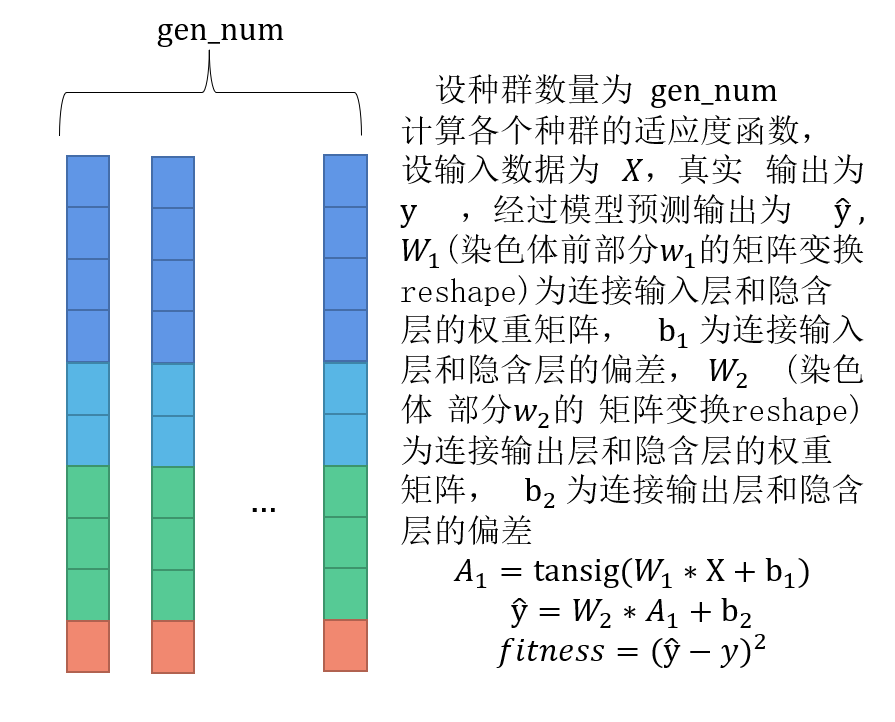
3. 遗传、交叉、变异
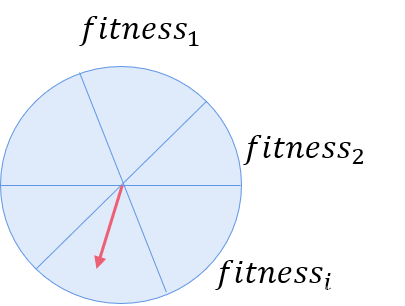
计算上一个种群的适应度函数,适应度越大对应的概率越大,越容易被选择,因此通过轮盘赌可以选择出适应度比较大的染色体。
接下来就是交叉和变异,本质就是增加种群的多样性,下次迭代最佳适应种群可能就出现在交叉或者变异后的个体。
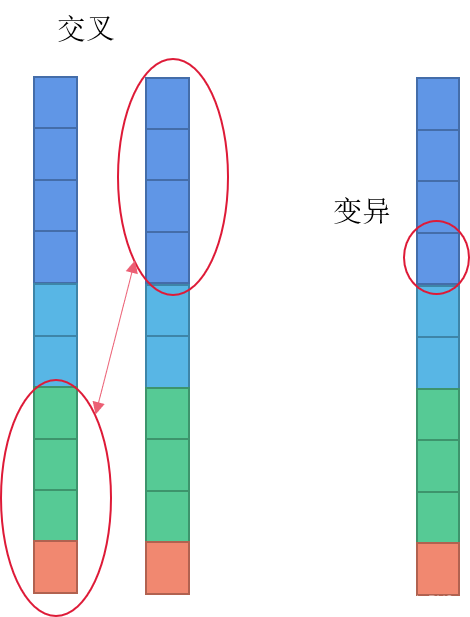
最后将遗传交叉变异过后的染色体组成新的种群进行下一次迭代。在经过一定迭代次数后挑出适应度最高的染色体作为最后的结果。
GA-BP神经网络MATLAB源码
实现形式(一)
对网络参数初始化后再反向传播进行优化,找出最优的初始化参数。
- 主函数
%% 准备数据
clc;clear;close all;
load('abalone_data.mat')%鲍鱼数据
%% 导入数据
%设置训练数据和测试数据
[m,n]=size(data);
train_num=round(0.8*m); %自变量
x_train_data=data(1:train_num,1:n-1);
y_train_data=data(1:train_num,n);
%测试数据
x_test_data=data(train_num+1:end,1:n-1);
y_test_data=data(train_num+1:end,n);
x_train_data=x_train_data';
y_train_data=y_train_data';
x_test_data=x_test_data';
%% 标准化
[x_train_regular,x_train_maxmin] = mapminmax(x_train_data);
[y_train_regular,y_train_maxmin] = mapminmax(y_train_data);
%% 初始化参数
EMS_all=[];
TIME=[];
num_iter_all=5;
for NN=1:num_iter_all
input_num=size(x_train_data,1); %输入特征个数
hidden_num=6; %隐藏层神经元个数
output_num=size(y_train_data,1); %输出特征个数
% 遗传算法参数初始化
iter_num=20; %总体进化迭代次数
group_num=10; %种群规模
cross_pro=0.4; %交叉概率
mutation_pro=0.05; %变异概率,相对来说比较小
%这个优化的主要思想就是优化网络参数的初始选择,初始选择对于效果好坏是有较大影响的
num_all=input_num*hidden_num+hidden_num+hidden_num*output_num+output_num;%网络总参数,只含一层隐藏层
lenchrom=ones(1,num_all); %种群总长度
limit=[-2*ones(num_all,1) 2*ones(num_all,1)]; %初始参数给定范围
t1=clock;
%% 初始化种群
input_data=x_train_regular;
output_data=y_train_regular;
for i=1:group_num
initial=rand(1,length(lenchrom)); %产生0-1的随机数
initial_chrom(i,:)=limit(:,1)'+(limit(:,2)-limit(:,1))'.*initial; %变成染色体的形式,一行为一条染色体
fitness_value=fitness1(initial_chrom(i,:),input_num,hidden_num,output_num,input_data,output_data);
fitness_group(i)=fitness_value;
end
[bestfitness,bestindex]=min(fitness_group);
bestchrom=initial_chrom(bestindex,:); %最好的染色体
avgfitness=sum(fitness_group)/group_num; %染色体的平均适应度
trace=[avgfitness bestfitness]; % 记录每一代进化中最好的适应度和平均适应度
%% 迭代过程
input_chrom=initial_chrom;
% iter_num=1;
for num=1:iter_num
% 选择
[new_chrom,new_fitness]=select(input_chrom,fitness_group,group_num); %把表现好的挑出来,还是和种群数量一样
% avgfitness=sum(new_fitness)/group_num;
%交叉
new_chrom=Cross(cross_pro,lenchrom,new_chrom,group_num,limit);
% 变异
new_chrom=Mutation(mutation_pro,lenchrom,new_chrom,group_num,num,iter_num,limit);
% 计算适应度
for j=1:group_num
sgroup=new_chrom(j,:); %个体
new_fitness(j)=fitness1(sgroup,input_num,hidden_num,output_num,input_data,output_data);
end
%找到最小和最大适应度的染色体及它们在种群中的位置
[newbestfitness,newbestindex]=min(new_fitness);
[worestfitness,worestindex]=max(new_fitness);
% 代替上一次进化中最好的染色体
if bestfitness>newbestfitness
bestfitness=newbestfitness;
bestchrom=new_chrom(newbestindex,:);
end
new_chrom(worestindex,:)=bestchrom;
new_fitness(worestindex)=bestfitness;
avgfitness=sum(new_fitness)/group_num;
trace=[trace;avgfitness bestfitness]; %记录每一代进化中最好的适应度和平均适应度
end
%%
figure(1)
[r ,~]=size(trace);
plot([1:r]',trace(:,2),'b--');
title(['适应度曲线 ' '终止代数=' num2str(iter_num)]);
xlabel('进化代数');ylabel('适应度');
legend('最佳适应度');
%% 把最优初始阀值权值赋予网络预测
% %用遗传算法优化的BP网络进行值预测
net=newff(x_train_regular,y_train_regular,hidden_num,{'tansig','purelin'});
w1=bestchrom(1:input_num*hidden_num); %输入和隐藏层之间的权重参数
B1=bestchrom(input_num*hidden_num+1:input_num*hidden_num+hidden_num); %隐藏层神经元的偏置
w2=bestchrom(input_num*hidden_num+hidden_num+1:input_num*hidden_num+...
hidden_num+hidden_num*output_num); %隐藏层和输出层之间的偏置
B2=bestchrom(input_num*hidden_num+hidden_num+hidden_num*output_num+1:input_num*hidden_num+...
hidden_num+hidden_num*output_num+output_num); %输出层神经元的偏置
%网络权值赋值
net.iw{1,1}=reshape(w1,hidden_num,input_num);
net.lw{2,1}=reshape(w2,output_num,hidden_num);
net.b{1}=reshape(B1,hidden_num,1);
net.b{2}=reshape(B2,output_num,1);
net.trainParam.epochs=200; %最大迭代次数
net.trainParam.lr=0.1; %学习率
net.trainParam.goal=0.00001;
[net,~]=train(net,x_train_regular,y_train_regular);
%将输入数据归一化
x_test_regular = mapminmax('apply',x_test_data,x_train_maxmin);
%放入到网络输出数据
y_test_regular=sim(net,x_test_regular);
%将得到的数据反归一化得到预测数据
GA_BP_predict=mapminmax('reverse',y_test_regular,y_train_maxmin);
errors_nn=sum(abs(GA_BP_predict'-y_test_data)./(y_test_data))/length(y_test_data);
EcRMSE=sqrt(sum((errors_nn).^2)/length(errors_nn));
t2=clock;
Time_all=etime(t2,t1);
EMS_all=[EMS_all,EcRMSE];
TIME=[TIME,Time_all];
end
%%
figure(2)
% EMS_all=[0.149326909497551,0.142964890977319,0.145465721759172,0.144173052409406,0.155684223205026,0.142331921077465,0.144810383902860,0.144137917725977,0.149229175194219,0.143762158676095];
plot(EMS_all,'LineWidth',2)
xlabel('实验次数')
ylabel('误差')
hold on
figure(3)
color=[111,168,86;128,199,252;112,138,248;184,84,246]/255;
plot(y_test_data,'Color',color(2,:),'LineWidth',1)
hold on
plot(GA_BP_predict,'*','Color',color(1,:))
hold on
legend('真实数据','预测数据')
disp('相对误差为:')
disp(EcRMSE)
titlestr=['BP神经网络',' 误差为:',num2str(min(EcRMSE))];
title(titlestr)
- 适应度函数
function fitness_value=fitness1(input_chrom,input_num,hidden_num,output_num,input_data,output_data)
%该函数用来计算适应度值
%input_chrom 输入种群
%input_num 输入层的节点数,即数据特征数量
%output_num 隐含层节点数,隐藏层神经元的个数
%input_data 训练输入数据
%output_data 训练输出数据
%fitness_value 个体适应度值
w1=input_chrom(1:input_num*hidden_num); %输入和隐藏层之间的权重参数
B1=input_chrom(input_num*hidden_num+1:input_num*hidden_num+hidden_num); %隐藏层神经元的偏置
w2=input_chrom(input_num*hidden_num+hidden_num+1:input_num*hidden_num+...
hidden_num+hidden_num*output_num); %隐藏层和输出层之间的偏置
B2=input_chrom(input_num*hidden_num+hidden_num+hidden_num*output_num+1:input_num*hidden_num+...
hidden_num+hidden_num*output_num+output_num); %输出层神经元的偏置
% %网络权值赋值
net=newff(input_data,output_data,hidden_num,{'tansig','purelin'});
%网络进化参数
net.trainParam.epochs=20;
net.trainParam.lr=0.1;
net.trainParam.goal=0.00001;
net.trainParam.show=100;
net.trainParam.showWindow=0;
%网络权值赋值
net.iw{1,1}=reshape(w1,hidden_num,input_num);
net.lw{2,1}=reshape(w2,output_num,hidden_num);
net.b{1}=reshape(B1,hidden_num,1);
net.b{2}=reshape(B2,output_num,1);
%网络训练
net=train(net,input_data,output_data);
pre=sim(net,input_data);
error=sum(sum(abs(pre-output_data)));
fitness_value=error; %误差即为适应度
end
- 选择函数
function [new_chrom,new_fitness]=select(input_chrom,fitness_group,group_num)
% 用轮盘赌在原来的函数里选择
% fitness_group 种群信息
% group_num 种群规模
% newgroup 选择后的新种群
%求适应度值倒数
fitness1=10./fitness_group; %individuals.fitness为个体适应度值
%个体选择概率
sumfitness=sum(fitness1);
sumf=fitness1./sumfitness;
%采用轮盘赌法选择新个体
index=[];
for i=1:1000 %group_num为种群数
pick=rand;
while pick==0
pick=rand;
end
for j=1:group_num
pick=pick-sumf(j);
if pick<0
index=[index j];
break;
end
end
if length(index) == group_num
break;
end
end
%新种群
new_chrom=input_chrom(index,:);
new_fitness=fitness_group(index);
end
- 交叉函数
function new_chrom=Cross(cross_pro,lenchrom,input_chrom,group_num,limit)
%随机选择两个染色体位置交叉
% cross_pro 交叉概率
% lenchrom 染色体的长度,即所有参数的数量
% input_chrom 染色体群,经过选择遗传下来的表现比较好的
% group_num 种群规模
% new_chrom 交叉后的染色体
for i=1:group_num %每一轮for循环中,可能会进行一次交叉操作,染色体是随机选择的,交叉位置也是随机选择的,
%但该轮for循环中是否进行交叉操作则由交叉概率决定(continue控制)
pick=rand(1,2); % 随机选择两个染色体进行交叉
while prod(pick)==0 %连乘
pick=rand(1,2);
end
index=ceil(pick.*group_num); % 交叉概率决定是否进行交叉
pick=rand;
while pick==0
pick=rand;
end
if pick>cross_pro
continue;
end
% 随机选择交叉位
pick=rand;
while pick==0
pick=rand;
end
flag=0;
while flag==0
pos=ceil(pick*length(lenchrom)); %随机选择进行交叉的位置,即选择第几个变量进行交叉,注意:两个染色体交叉的位置相同
pick=rand; %交叉开始
v1=input_chrom(index(1),pos);
v2=input_chrom(index(2),pos);
input_chrom(index(1),pos)=pick*v2+(1-pick)*v1;
input_chrom(index(2),pos)=pick*v1+(1-pick)*v2; %交叉结束
%判断交叉后的两条染色体可不可行
limit1=mean(limit);
f11=isempty(find(input_chrom(index(1),:)>limit1(2)));
f12=isempty(find(input_chrom(index(1),:)<limit1(1)));
if f11*f12==0
flag1=0;
else
flag1=1;
end
f21=isempty(find(input_chrom(index(2),:)>limit1(2)));
f22=isempty(find(input_chrom(index(2),:)<limit1(1)));
if f21*f22==0
flag2=0;
else
flag2=1;
end
if flag1*flag2==0
flag=0;
else
flag=1;
end %如果两个染色体不是都可行,则重新交叉
end
end
new_chrom=input_chrom;
end
- 变异函数
function new_chrom=Mutation(mutation_pro,lenchrom,input_chrom,group_num,num,iter_num,limit)
% 本函数完成变异操作
% mutation_pro 变异概率
% lenchrom 染色体长度
% input_chrom 输入交叉过后的染色体
% group_num 种群规模
% iter_num 最大迭代次数
% limit 每个个体的上限和下限
% num 当前迭代次数
% new_chrom 变异后的染色体
for i=1:group_num %每一轮for循环中,可能会进行一次变异操作,染色体是随机选择的,变异位置也是随机选择的,
%但该轮for循环中是否进行变异操作则由变异概率决定(continue控制)
% 随机选择一个染色体进行变异
pick=rand;
while pick==0
pick=rand;
end
index=ceil(pick*group_num);
% 变异概率决定该轮循环是否进行变异
pick=rand;
if pick>mutation_pro
continue;
end
flag=0;
while flag==0
% 变异位置
pick=rand;
while pick==0
pick=rand;
end
pos=ceil(pick*sum(lenchrom)); %随机选择了染色体变异的位置,即选择了第pos个变量进行变异
pick=rand; %变异开始
fg=(pick*(1-num/iter_num))^2;
if pick>0.5
input_chrom(index,pos)=input_chrom(index,pos)+(limit(pos,2)-input_chrom(index,pos))*fg;
else
input_chrom(index,pos)=input_chrom(index,pos)-(input_chrom(index,pos)-limit(pos,1))*fg;
end %变异结束
limit1=mean(limit);
f1=isempty(find(input_chrom(index,:)>limit1(2)));
f2=isempty(find(input_chrom(index,:)<limit1(1)));
if f1*f2==0
flag=0;
else
flag=1;
end
end
end
new_chrom=input_chrom;
可以设置num_iter_all=1 即运行一次,把种群数和迭代次数都设置大一些
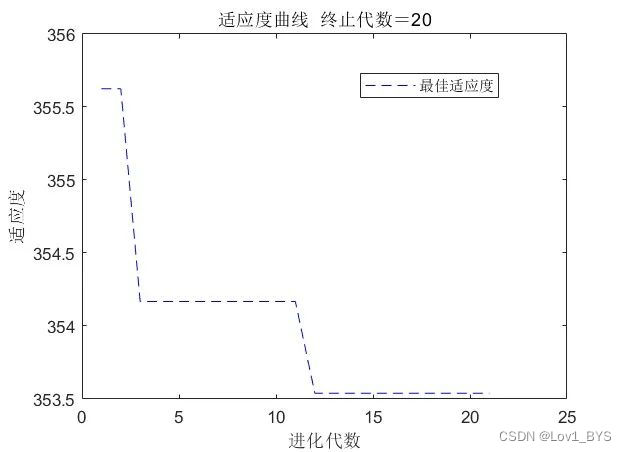

实现形式(二)
对网络参数初始化正向传播进行优化,找出最优的初始化参数,最后再反向传播进行优化
- 主函数
%% 准备数据
clc;clear;close all;
load('abalone_data.mat')%鲍鱼数据
%% 导入数据
%设置训练数据和测试数据
[m,n]=size(data);
train_num=round(0.8*m); %自变量
x_train_data=data(1:train_num,1:n-1);
y_train_data=data(1:train_num,n);
%测试数据
x_test_data=data(train_num+1:end,1:n-1);
y_test_data=data(train_num+1:end,n);
x_train_data=x_train_data';
y_train_data=y_train_data';
x_test_data=x_test_data';
%% 标准化
[x_train_regular,x_train_maxmin] = mapminmax(x_train_data);
[y_train_regular,y_train_maxmin] = mapminmax(y_train_data);
%% 初始化参数
EMS_all=[];
TIME=[];
num_iter_all=5;
for NN=1:num_iter_all
input_num=size(x_train_data,1); %输入特征个数
hidden_num=6; %隐藏层神经元个数
output_num=size(y_train_data,1); %输出特征个数
% 遗传算法参数初始化
iter_num=30; %总体进化迭代次数
group_num=10; %种群规模
cross_pro=0.4; %交叉概率
mutation_pro=0.05; %变异概率,相对来说比较小
%这个优化的主要思想就是优化网络参数的初始选择,初始选择对于效果好坏是有较大影响的
num_all=input_num*hidden_num+hidden_num+hidden_num*output_num+output_num;%网络总参数,只含一层隐藏层
lenchrom=ones(1,num_all); %种群总长度
limit=[-2*ones(num_all,1) 2*ones(num_all,1)]; %初始参数给定范围
t1=clock;
%% 初始化种群
input_data=x_train_regular;
output_data=y_train_regular;
for i=1:group_num
initial=rand(1,length(lenchrom)); %产生0-1的随机数
initial_chrom(i,:)=limit(:,1)'+(limit(:,2)-limit(:,1))'.*initial; %变成染色体的形式,一行为一条染色体
fitness_value=fitness(initial_chrom(i,:),input_num,hidden_num,output_num,input_data,output_data);
fitness_group(i)=fitness_value;
end
[bestfitness,bestindex]=min(fitness_group);
bestchrom=initial_chrom(bestindex,:); %最好的染色体
avgfitness=sum(fitness_group)/group_num; %染色体的平均适应度
trace=[avgfitness bestfitness]; % 记录每一代进化中最好的适应度和平均适应度
%% 迭代过程
new_chrom=initial_chrom;
new_fitness=fitness_group;
for num=1:iter_num
% 选择
[new_chrom,new_fitness]=select(new_chrom,new_fitness,group_num); %把表现好的挑出来,还是和种群数量一样
%交叉
new_chrom=Cross(cross_pro,lenchrom,new_chrom,group_num,limit);
% 变异
new_chrom=Mutation(mutation_pro,lenchrom,new_chrom,group_num,num,iter_num,limit);
% 计算适应度
for j=1:group_num
sgroup=new_chrom(j,:); %个体
new_fitness(j)=fitness(sgroup,input_num,hidden_num,output_num,input_data,output_data);
end
%找到最小和最大适应度的染色体及它们在种群中的位置
[newbestfitness,newbestindex]=min(new_fitness);
[worestfitness,worestindex]=max(new_fitness);
% 代替上一次进化中最好的染色体
if bestfitness>newbestfitness
bestfitness=newbestfitness;
bestchrom=new_chrom(newbestindex,:);
end
new_chrom(worestindex,:)=bestchrom;
new_fitness(worestindex)=bestfitness;
avgfitness=sum(new_fitness)/group_num;
trace=[trace;avgfitness bestfitness]; %记录每一代进化中最好的适应度和平均适应度
end
%%
figure(1)
[r ,~]=size(trace);
plot([1:r]',trace(:,2),'b--');
title(['适应度曲线 ' '终止代数=' num2str(iter_num)]);
xlabel('进化代数');ylabel('适应度');
legend('最佳适应度');
%% 把最优初始阀值权值赋予网络预测
% %用遗传算法优化的BP网络进行值预测
net=newff(x_train_regular,y_train_regular,hidden_num,{'tansig','purelin'},'trainlm');
w1=bestchrom(1:input_num*hidden_num); %输入和隐藏层之间的权重参数
B1=bestchrom(input_num*hidden_num+1:input_num*hidden_num+hidden_num); %隐藏层神经元的偏置
w2=bestchrom(input_num*hidden_num+hidden_num+1:input_num*hidden_num+...
hidden_num+hidden_num*output_num); %隐藏层和输出层之间的偏置
B2=bestchrom(input_num*hidden_num+hidden_num+hidden_num*output_num+1:input_num*hidden_num+...
hidden_num+hidden_num*output_num+output_num); %输出层神经元的偏置
%网络权值赋值
net.iw{1,1}=reshape(w1,hidden_num,input_num);
net.lw{2,1}=reshape(w2,output_num,hidden_num);
net.b{1}=reshape(B1,hidden_num,1);
net.b{2}=reshape(B2,output_num,1);
net.trainParam.epochs=200; %最大迭代次数
net.trainParam.lr=0.1; %学习率
net.trainParam.goal=0.00001;
[net,~]=train(net,x_train_regular,y_train_regular);
%将输入数据归一化
x_test_regular = mapminmax('apply',x_test_data,x_train_maxmin);
%放入到网络输出数据
y_test_regular=sim(net,x_test_regular);
%将得到的数据反归一化得到预测数据
GA_BP_predict=mapminmax('reverse',y_test_regular,y_train_maxmin);
errors_nn=sum(abs(GA_BP_predict'-y_test_data)./(y_test_data))/length(y_test_data);
EcRMSE=sqrt(sum((errors_nn).^2)/length(errors_nn));
t2=clock;
Time_all=etime(t2,t1);
EMS_all=[EMS_all,EcRMSE];
TIME=[TIME,Time_all];
end
figure(2)
% EMS_all=[0.149326909497551,0.142964890977319,0.145465721759172,0.144173052409406,0.155684223205026,0.142331921077465,0.144810383902860,0.144137917725977,0.149229175194219,0.143762158676095];
plot(EMS_all,'LineWidth',2)
xlabel('实验次数')
ylabel('误差')
hold on
figure(3)
color=[111,168,86;128,199,252;112,138,248;184,84,246]/255;
plot(y_test_data,'Color',color(2,:),'LineWidth',1)
hold on
plot(GA_BP_predict,'*','Color',color(1,:))
hold on
legend('真实数据','预测数据')
disp('相对容量误差为:')
disp(EcRMSE)
titlestr=['BP神经网络',' 误差为:',num2str(min(EcRMSE))];
title(titlestr)
- 适应度函数
function fitness_value=fitness(input_chrom,input_num,hidden_num,output_num,input_data,output_data)
%该函数用来计算适应度值
%input_chrom 输入种群
%input_num 输入层的节点数,即数据特征数量
%output_num 隐含层节点数,隐藏层神经元的个数
%input_data 训练输入数据
%output_data 训练输出数据
%fitness_value 个体适应度值
w1=input_chrom(1:input_num*hidden_num); %输入和隐藏层之间的权重参数
B1=input_chrom(input_num*hidden_num+1:input_num*hidden_num+hidden_num); %隐藏层神经元的偏置
w2=input_chrom(input_num*hidden_num+hidden_num+1:input_num*hidden_num+...
hidden_num+hidden_num*output_num); %隐藏层和输出层之间的偏置
B2=input_chrom(input_num*hidden_num+hidden_num+hidden_num*output_num+1:input_num*hidden_num+...
hidden_num+hidden_num*output_num+output_num); %输出层神经元的偏置
%网络权值赋值
W1=reshape(w1,hidden_num,input_num);
W2=reshape(w2,output_num,hidden_num);
B1=reshape(B1,hidden_num,1);
B2=reshape(B2,output_num,1);
[~,n]=size(input_data);
A1=tansig(W1*input_data+repmat(B1,1,n)); %需与main函数中激活函数相同
A2=purelin(W2*A1+repmat(B2,1,n)); %需与main函数中激活函数相同
error=sumsqr(output_data-A2);
fitness_value=error; %误差即为适应度
end
- 选择函数
function [new_chrom,new_fitness]=select(input_chrom,fitness_group,group_num)
% 用轮盘赌在原来的函数里选择
% fitness_group 种群信息
% group_num 种群规模
% newgroup 选择后的新种群
%求适应度值倒数
fitness1=10./fitness_group; %individuals.fitness为个体适应度值
%个体选择概率
sumfitness=sum(fitness1);
sumf=fitness1./sumfitness;
%采用轮盘赌法选择新个体
index=[];
for i=1:1000 %group_num为种群数
pick=rand;
while pick==0
pick=rand;
end
for j=1:group_num
pick=pick-sumf(j);
if pick<0
index=[index j];
break;
end
end
if length(index) == group_num
break;
end
end
%新种群
new_chrom=input_chrom(index,:);
new_fitness=fitness_group(index);
end
- 交叉函数
function new_chrom=Cross(cross_pro,lenchrom,input_chrom,group_num,limit)
%随机选择两个染色体位置交叉
% cross_pro 交叉概率
% lenchrom 染色体的长度,即所有参数的数量
% input_chrom 染色体群,经过选择遗传下来的表现比较好的
% group_num 种群规模
% new_chrom 交叉后的染色体
for i=1:group_num %每一轮for循环中,可能会进行一次交叉操作,染色体是随机选择的,交叉位置也是随机选择的,
%但该轮for循环中是否进行交叉操作则由交叉概率决定(continue控制)
pick=rand(1,2); % 随机选择两个染色体进行交叉
while prod(pick)==0 %连乘
pick=rand(1,2);
end
index=ceil(pick.*group_num); % 交叉概率决定是否进行交叉
pick=rand;
while pick==0
pick=rand;
end
if pick>cross_pro
continue;
end
% 随机选择交叉位
pick=rand;
while pick==0
pick=rand;
end
flag=0;
while flag==0
pos=ceil(pick*length(lenchrom)); %随机选择进行交叉的位置,即选择第几个变量进行交叉,注意:两个染色体交叉的位置相同
pick=rand; %交叉开始
v1=input_chrom(index(1),pos);
v2=input_chrom(index(2),pos);
input_chrom(index(1),pos)=pick*v2+(1-pick)*v1;
input_chrom(index(2),pos)=pick*v1+(1-pick)*v2; %交叉结束
%判断交叉后的两条染色体可不可行
limit1=mean(limit);
f11=isempty(find(input_chrom(index(1),:)>limit1(2)));
f12=isempty(find(input_chrom(index(1),:)<limit1(1)));
if f11*f12==0
flag1=0;
else
flag1=1;
end
f21=isempty(find(input_chrom(index(2),:)>limit1(2)));
f22=isempty(find(input_chrom(index(2),:)<limit1(1)));
if f21*f22==0
flag2=0;
else
flag2=1;
end
if flag1*flag2==0
flag=0;
else
flag=1;
end %如果两个染色体不是都可行,则重新交叉
end
end
new_chrom=input_chrom;
end
- 变异函数
function new_chrom=Mutation(mutation_pro,lenchrom,input_chrom,group_num,num,iter_num,limit)
% 本函数完成变异操作
% mutation_pro 变异概率
% lenchrom 染色体长度
% input_chrom 输入交叉过后的染色体
% group_num 种群规模
% iter_num 最大迭代次数
% limit 每个个体的上限和下限
% num 当前迭代次数
% new_chrom 变异后的染色体
for i=1:group_num %每一轮for循环中,可能会进行一次变异操作,染色体是随机选择的,变异位置也是随机选择的,
%但该轮for循环中是否进行变异操作则由变异概率决定(continue控制)
% 随机选择一个染色体进行变异
pick=rand;
while pick==0
pick=rand;
end
index=ceil(pick*group_num);
% 变异概率决定该轮循环是否进行变异
pick=rand;
if pick>mutation_pro
continue;
end
flag=0;
while flag==0
% 变异位置
pick=rand;
while pick==0
pick=rand;
end
pos=ceil(pick*sum(lenchrom)); %随机选择了染色体变异的位置,即选择了第pos个变量进行变异
pick=rand; %变异开始
fg=(pick*(1-num/iter_num))^2;
if pick>0.5
input_chrom(index,pos)=input_chrom(index,pos)+(limit(pos,2)-input_chrom(index,pos))*fg;
else
input_chrom(index,pos)=input_chrom(index,pos)-(input_chrom(index,pos)-limit(pos,1))*fg;
end %变异结束
limit1=mean(limit);
f1=isempty(find(input_chrom(index,:)>limit1(2)));
f2=isempty(find(input_chrom(index,:)<limit1(1)));
if f1*f2==0
flag=0;
else
flag=1;
end
end
end
new_chrom=input_chrom;
这种方法和之前效果好像差不多,之前迭代次数没有设置那么多,这次迭代100次运行时间也只需要1秒多,差不多是之前那种方法运行速度的100倍。
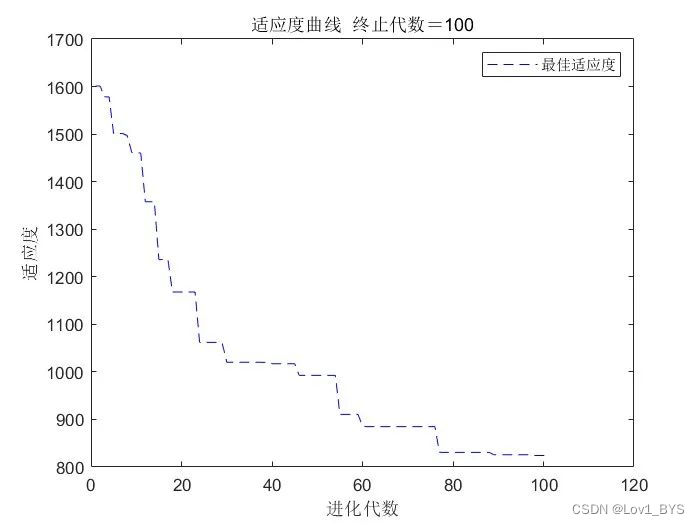
实现形式(三)
不引入反向传播只用遗传算法优化网络参数,试了下还是反向传播优化效果好,除非遗传算法种群很大,迭代次数特别多才勉强可达到反向传播的效果,这样运行时间也会非常长
%% 准备数据
clc;clear;close all;
load('abalone_data.mat')%鲍鱼数据
%% 导入数据
%设置训练数据和测试数据
[m,n]=size(data);
train_num=round(0.8*m); %自变量
x_train_data=data(1:train_num,1:n-1);
y_train_data=data(1:train_num,n);
%测试数据
x_test_data=data(train_num+1:end,1:n-1);
y_test_data=data(train_num+1:end,n);
x_train_data=x_train_data';
y_train_data=y_train_data';
x_test_data=x_test_data';
%% 标准化
[x_train_regular,x_train_maxmin] = mapminmax(x_train_data);
[y_train_regular,y_train_maxmin] = mapminmax(y_train_data);
%% 初始化参数
input_num=size(x_train_data,1); %输入特征个数
hidden_num=6; %隐藏层神经元个数
output_num=size(y_train_data,1); %输出特征个数
% 遗传算法参数初始化
iter_num=500; %总体进化迭代次数
group_num=40; %种群规模
cross_pro=0.4; %交叉概率
mutation_pro=0.05; %变异概率,相对来说比较小
%这个优化的主要思想就是优化网络参数的初始选择,初始选择对于效果好坏是有较大影响的
num_all=input_num*hidden_num+hidden_num+hidden_num*output_num+output_num;%网络总参数,只含一层隐藏层
lenchrom=ones(1,num_all); %种群总长度
limit=[-1*ones(num_all,1) 1*ones(num_all,1)]; %初始参数给定范围
EMS_all=[];
TIME=[];
num_iter_all=1;
for NN=1:num_iter_all
t1=clock;
%% 初始化种群
input_data=x_train_regular;
output_data=y_train_regular;
for i=1:group_num
initial=rand(1,length(lenchrom)); %产生0-1的随机数
initial_chrom(i,:)=limit(:,1)'+(limit(:,2)-limit(:,1))'.*initial; %变成染色体的形式,一行为一条染色体
fitness_value=fitness(initial_chrom(i,:),input_num,hidden_num,output_num,input_data,output_data);
fitness_group(i)=fitness_value;
end
[bestfitness,bestindex]=min(fitness_group);
bestchrom=initial_chrom(bestindex,:); %最好的染色体
avgfitness=sum(fitness_group)/group_num; %染色体的平均适应度
trace=[avgfitness bestfitness]; % 记录每一代进化中最好的适应度和平均适应度
%% 迭代过程
new_chrom=initial_chrom;
new_fitness=fitness_group;
for num=1:iter_num
% 选择
[new_chrom,new_fitness]=select(new_chrom,new_fitness,group_num);
avgfitness=sum(new_fitness)/group_num;
%交叉
new_chrom=Cross(cross_pro,lenchrom,new_chrom,group_num,limit);
% 变异
new_chrom=Mutation(mutation_pro,lenchrom,new_chrom,group_num,num,iter_num,limit);
% 计算适应度
for j=1:group_num
sgroup=new_chrom(j,:); %个体
new_fitness(j)=fitness(sgroup,input_num,hidden_num,output_num,input_data,output_data);
end
%找到最小和最大适应度的染色体及它们在种群中的位置
[newbestfitness,newbestindex]=min(new_fitness);
[worestfitness,worestindex]=max(new_fitness);
% 代替上一次进化中最好的染色体
if bestfitness>newbestfitness
bestfitness=newbestfitness;
bestchrom=new_chrom(newbestindex,:);
end
new_chrom(worestindex,:)=bestchrom;
new_fitness(worestindex)=bestfitness;
avgfitness=sum(new_fitness)/group_num;
trace=[trace;avgfitness bestfitness]; %记录每一代进化中最好的适应度和平均适应度
end
%%
figure(1)
[r ,~]=size(trace);
plot([1:r]',trace(:,2),'b--');
title(['适应度曲线 ' '终止代数=' num2str(iter_num)]);
xlabel('进化代数');ylabel('适应度');
legend('最佳适应度');
%% 把最优初始阀值权值赋予网络预测
% %用遗传算法优化的BP网络进行值预测
% net=newff(x_train_regular,y_train_regular,hidden_num,{'tansig','purelin'},'trainlm');
% input_chrom=bestchrom;
w1=bestchrom(1:input_num*hidden_num); %输入和隐藏层之间的权重参数
B1=bestchrom(input_num*hidden_num+1:input_num*hidden_num+hidden_num); %隐藏层神经元的偏置
w2=bestchrom(input_num*hidden_num+hidden_num+1:input_num*hidden_num+...
hidden_num+hidden_num*output_num); %隐藏层和输出层之间的偏置
B2=bestchrom(input_num*hidden_num+hidden_num+hidden_num*output_num+1:input_num*hidden_num+...
hidden_num+hidden_num*output_num+output_num); %输出层神经元的偏置
%网络权值赋值
% net.iw{1,1}=reshape(w1,hidden_num,input_num);
% net.lw{2,1}=reshape(w2,output_num,hidden_num);
% net.b{1}=reshape(B1,hidden_num,1);
% net.b{2}=reshape(B2,output_num,1);
% net.trainParam.epochs=200; %最大迭代次数
% net.trainParam.lr=0.1; %学习率
% net.trainParam.goal=0.00001;
% [net,~]=train(net,x_train_regular,y_train_regular);
w1=reshape(w1,hidden_num,input_num);
w2=reshape(w2,output_num,hidden_num);
B1=reshape(B1,hidden_num,1);
B2=reshape(B2,output_num,1);
%将输入数据归一化
x_test_regular = mapminmax('apply',x_test_data,x_train_maxmin);
[~,n1]=size(x_test_regular);
%放入到网络输出数据
A1=tansig(w1*x_test_regular+repmat(B1,1,n1)); %需与main函数中激活函数相同
A2=purelin(w2*A1+repmat(B2,1,n1)); %需与main函数中激活函数相同
% y_test_regular=sim(net,x_test_regular);
y_test_regular=A2;
%将得到的数据反归一化得到预测数据
GA_BP_predict=mapminmax('reverse',y_test_regular,y_train_maxmin);
errors_nn=sum(abs(GA_BP_predict'-y_test_data)./(y_test_data))/length(y_test_data);
EcRMSE=sqrt(sum((errors_nn).^2)/length(errors_nn));
t2=clock;
Time_all=etime(t2,t1);
EMS_all=[EMS_all,EcRMSE];
TIME=[TIME,Time_all];
end
figure(2)
% EMS_all=[0.142257836480101,0.145475762362687,0.142025031462931,0.144898144312287,0.145330361342209,0.151655962592779,0.142833464193844,0.136991568565291,0.150775201950770,0.146993509081267];
plot(EMS_all,'LineWidth',2)
xlabel('实验次数')
ylabel('误差')
hold on
figure(3)
color=[111,168,86;128,199,252;112,138,248;184,84,246]/255;
plot(y_test_data,'Color',color(2,:),'LineWidth',1)
hold on
plot(GA_BP_predict,'*','Color',color(1,:))
hold on
legend('真实数据','预测数据')
disp('相对容量误差为:')
disp(EcRMSE)
titlestr=['BP神经网络',' 误差为:',num2str(min(EcRMSE))];
title(titlestr)
newff : 搭建神经网络
- 语法
newff(P,T,S,TF,BTF,BLF,PF,IPF,OPF,DDF)说明
- newff(P,T,S,TF,BTF,BLF,PF,IPF,OPF,DDF),
P为输入数据,T为输入标签,S为神经元个数,TF为激活函数,返回训练好的模型。
























 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










