倾向得分匹配法：从观察数据中提取因果关系的有力工具

1. 例子引入：医疗决策中的困境

本文首先引入一个例子来为后续说明提供更加直观的解释

刘医生面临一个棘手的问题：新型降压药物A是否真的比传统药物B更有效，更能降低患者血压？虽然初步数据显示使用药物A的患者血压下降更明显，但张医生注意到一个关键问题——选择使用药物A的患者普遍年龄较轻、病情较轻，而药物B多被用于年长且病情较重的患者。

这种非随机的治疗分配使得直接比较两组患者的结果变得不可靠。理想情况下，应进行随机对照试验，但由于伦理考虑、成本限制和时间约束，这往往不可行。

这正是倾向得分匹配法（Propensity Score Matching，PSM）大显身手的时刻。通过这种统计方法，张医生可以"模拟"一个随机试验环境，从而得出更可靠的结论。

让我们深入了解这一强大的统计工具如何帮助研究者从观察性数据中获取更可靠的因果推断。

2. 倾向得分匹配法的基本原理

2.1 基本概念

在刘医生的研究中，倾向得分代表患者接受新型降压药物A（而非传统药物B）的概率。这一概率基于患者的特征计算，如年龄、性别、初始血压、并发症和既往病史等。

倾向得分匹配的核心思想是：找到新药组和传统药组中倾向得分相似的患者进行匹配。例如，找到一位65岁、高血压程度中等、有糖尿病并发症的接受新药A的患者，与另一位具有类似特征但接受传统药B的患者进行比较。这样创建的"人工随机试验"可以有效减少选择偏差的影响。

2.2 为什么需要倾向得分匹配？

在刘医生的观察性研究中，药物选择不是随机的：

• 可能更年轻、病情较轻的患者被优先推荐使用新药A
• 经济条件较好的患者可能更容易选择新药
• 有特定并发症的患者可能被建议避免使用某种药物

这些系统性差异会导致直接比较结果产生误导性结论。通过倾向得分匹配，刘医生可以平衡两组间的基线特征差异，使分析更接近随机试验的结果。

3. 倾向得分匹配法的数学原理与应用解释

3.1 倾向得分定义

倾向得分由Rosenbaum和Rubin在1983年提出，定义为：

$$e(X)=P(Z=1|X)$$

在这个例子中，公式的实际含义如下：

• $e(X)$ 是患者接受新型降压药A的概率（倾向得分）
• $Z$ 是治疗指示变量（Z=1表示患者接受新药A，Z=0表示接受传统药B）
• $X$ 是患者特征向量，包括年龄、性别、初始血压值、血脂水平、并发症情况、既往病史等所有可能影响治疗选择和治疗结果的变量

例如，一位65岁、女性、初始收缩压为150mmHg、有糖尿病史的患者，可能有40%的概率被分配到新药A组（$e(X)=0.4$）。

3.2 关键假设

倾向得分匹配基于两个关键假设：

1. 条件独立性假设：给定观察到的协变量，治疗分配与潜在结果独立

$$(Y_0,Y_1)\perp Z|X$$

在刘医生的研究中，这意味着：在控制了所有观察到的患者特征（如年龄、性别、初始血压等）后，药物A或B的分配与患者在任一药物下的潜在血压结果无关。换句话说，没有未测量的因素同时影响药物选择和血压结果。

2. 共同支持假设：每个患者都有非零概率接受任一种药物

$$0<P(Z=1|X)<1$$

实际上，这意味着对于任何特征组合的患者，不能100%确定他们一定会接受某种特定药物。必须存在某种"偶然性"，使得任何特征的患者都有可能被分配到任一组。

3.3 平均处理效应计算

匹配后，刘医生可以估计平均治疗效应（ATE）：

$$ATE=E[Y_1-Y_0]=E[E[Y|Z=1,e(X)]-E[Y|Z=0,e(X)]]$$

在实际应用中，这代表：新药A相比传统药B对整个人群的平均降压效果。

或者他可能更关心处理组的平均治疗效应（ATT）：

$$ATT=E[Y_1-Y_0|Z=1]=E[E[Y|Z=1,e(X)]-E[Y|Z=0,e(X)]|Z=1]$$

这表示：对于那些实际接受了新药A的患者，如果他们接受传统药B，其降压效果的平均差异。这对于评估"实际使用新药的患者是否真的从中获益"尤为重要。

4. 倾向得分匹配的实施步骤：医疗研究实例

我们将通过刘医生的降压药研究来说明整个流程：

4.1 步骤详解

1. 选择协变量：刘医生收集了所有可能影响药物选择和降压效果的患者特征：

   • 人口学特征：年龄、性别、民族、教育水平、收入状况
   • 临床特征：初始血压、病程、BMI、既往心血管事件、肾功能指标
   • 生活方式：吸烟、饮酒、运动、饮食习惯
   • 并发症：糖尿病、高脂血症、心脏病、脑卒中史

2. 估计倾向得分：使用逻辑回归模型预测每位患者接受新药A的概率：

   逻辑回归：新药使用(是/否) ~ 年龄 + 性别 + 初始血压 + 并发症 + ...
   

3. 匹配方法：刘医生选择1:1最近邻匹配，为每位接受新药A的患者找到一位倾向得分最接近的接受传统药B的患者。

4. 评估匹配质量：比较匹配前后各特征的标准化差异，理想情况下差异应小于0.1。例如，匹配前两组患者的平均年龄差可能是10岁，匹配后差异缩小到1岁以内。

5. 估计处理效应：计算匹配样本中的平均收缩压和舒张压差异，发现新药A比传统药B平均多降低收缩压5mmHg。

6. 敏感性分析：考虑可能存在未测量的混杂因素（如依从性），评估这些因素需要多大影响才会改变结论。

5. 应用场景与实例扩展

倾向得分匹配在多个领域有广泛应用：

• 医学研究：如降压药研究，或评估手术方式选择对患者预后的影响
• 经济学：评估职业培训项目对失业者就业率和收入的影响
• 教育研究：特殊教育项目对学习成果的效果评估
• 社会科学：福利政策对贫困人口生活质量的影响
• 市场营销：不同营销策略对消费者购买行为的效果比较

6. 实际案例：课后补习班的学习效果评估

6.1 研究背景

王老师想知道学校新开设的课后补习班是否真的能提高学生的数学成绩。补习班每周两次，每次90分钟，为期一个学期。

关键问题是：参加补习班完全自愿，导致参加的学生和没参加的学生本身就有很大不同。

6.2 问题分析

王老师收集了100名参加补习班的学生和200名未参加补习班的学生的数据，发现直接比较两组的期末成绩会产生误导，因为：

• 参加补习班的学生上学期平均分是75分，而未参加的学生平均分是82分（成绩差的学生更愿意补习）
• 补习班中女生占65%，非补习班学生中女生只占45%
• 补习班学生中有家长陪伴学习的比例为70%，非补习班只有40%

这些系统性差异使得补习效果的直接比较不可靠。

6.3 应用倾向得分匹配的步骤

步骤1：收集学生特征信息

王老师收集了这些信息：

• 上学期数学成绩（60-100分）
• 性别（男/女）
• 是否有家长辅导（是/否）
• 平时是否喜欢数学（1-5分）
• 每天做作业的时间（小时）
• 课外阅读量（每周小时数）
• 是否参加其他兴趣班（是/否）

步骤2：计算每个学生参加补习班的可能性

王老师用一个简单的计算公式预测每个学生选择参加补习班的概率：

成绩低的学生更可能参加补习班，每少10分，参加概率增加30%
女生比男生更可能参加补习班，概率高出20%
有家长辅导的学生更可能参加补习班，概率高出40%

于是计算出：

• 小明：上学期65分，男生，有家长辅导 → 参加概率60%
• 小红：上学期85分，女生，有家长辅导 → 参加概率45%
• 小华：上学期90分，男生，无家长辅导 → 参加概率20%

步骤3：配对相似学生

王老师为每个参加补习班的学生找到一个没参加补习班但"参加概率"最接近的学生：

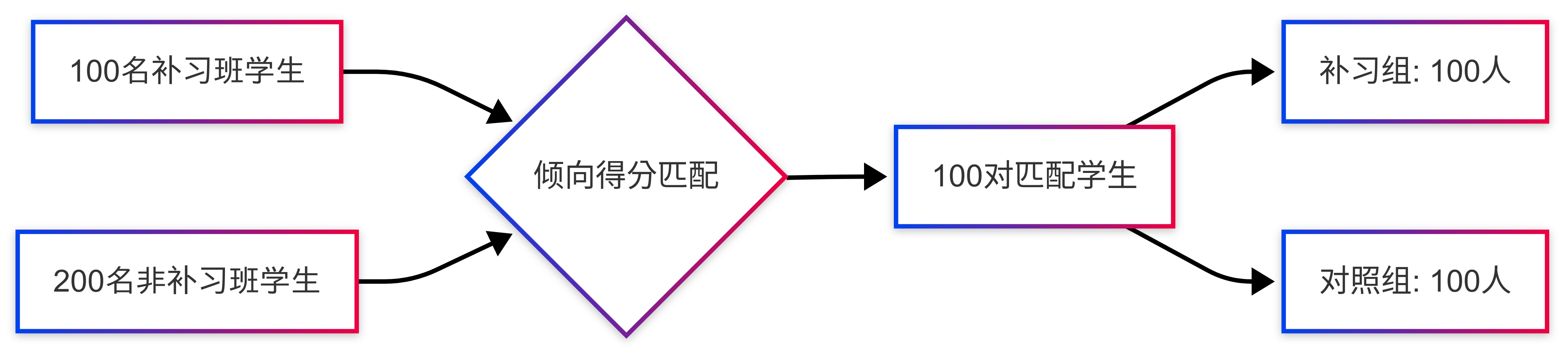
例如：

• 补习班的小明（参加概率60%）配对非补习班的小军（参加概率58%）
• 补习班的小红（参加概率45%）配对非补习班的小芳（参加概率44%）

步骤4：检查配对质量

配对前后学生特征对比：

• 上学期平均分差异：配对前相差7分，配对后相差0.8分
• 女生比例差异：配对前相差20个百分点，配对后相差3个百分点
• 家长辅导比例差异：配对前相差30个百分点，配对后相差2个百分点

王老师确认：通过配对，两组学生现在在各方面都非常相似了。

步骤5：比较真实效果

王老师比较了配对好的两组学生的期末成绩：

• 补习班学生期末平均分：83分
• 非补习班学生期末平均分：78分
• 差异：5分

步骤6：考虑其他可能因素

王老师思考了一些她没有测量的因素，比如学生的自我激励程度。她发现，除非有非常强大的未测量因素存在，否则补习班的正面效果仍然成立。

6.4 结果解释与建议

通过这种公平的比较方法，王老师可以更有信心地说：

1. 课后补习班确实能提高学生的数学成绩，平均提高约5分
2. 补习班对基础较弱的学生帮助最大，提高了约7分
3. 根据这些发现，她建议学校继续开设补习班，并特别鼓励基础较弱的学生参加

王老师向校长解释道：“通过倾向得分匹配，我们解决了’本来成绩就不同的学生’比较的问题，现在可以确定补习班的效果是真实的，而不仅仅是因为参加的学生和不参加的学生本身就不同。”

换句话说

这就像是一场公平的赛跑比赛。如果我们直接比较跑步俱乐部成员和普通人的速度，俱乐部成员肯定跑得快。但这不能说明加入俱乐部会让人跑得更快——可能只是跑得快的人才会加入俱乐部。

倾向得分匹配就是为每个俱乐部成员找一个"跑步天赋"相似但没加入俱乐部的人比较。这样，如果俱乐部成员还是跑得更快，我们才能说俱乐部训练真的有效。

7. 倾向得分匹配法的局限性与实践注意事项

尽管功能强大，倾向得分匹配仍有一些局限性：

1. 无法控制未观察到的混杂因素：如果某些重要因素（如个人主动性、职业适应能力）没有被测量，匹配就无法消除这些因素带来的偏差

2. 需要足够大的样本量：在刘医生的研究中，如果新药使用患者仅有20人，而传统药使用者有2000人，匹配的可能性就会受限

3. 模型依赖性：倾向得分的质量取决于用于估计它的模型是否正确。如果遗漏关键变量或关系被错误指定，匹配质量将受影响

4. 共同支持问题：如果某些特征的患者几乎总是接受某种特定治疗（如严重心脏病患者几乎都使用传统药物），就难以找到适当的匹配

8. 总结与实践指导

倾向得分匹配是一种强大的统计技术，通过模拟随机分配环境，帮助研究者从观察性数据中获得更可靠的因果推断。它通过平衡处理组和对照组之间的基线差异，减少选择偏差，提高研究结论的有效性。

对于实践研究者，建议：

1. 仔细选择并测量所有可能的混杂变量
2. 检查并报告匹配质量
3. 进行敏感性分析以评估结论稳健性
4. 承认方法局限性，谨慎解释研究发现

在无法进行随机对照试验的情况下，倾向得分匹配为研究者提供了一个实用且相对可靠的分析方法，帮助我们从复杂的观察数据中提取有价值的因果关系证据。

参考文献

1. Rosenbaum, P. R., & Rubin, D. B. (1983). The central role of the propensity score in observational studies for causal effects. Biometrika, 70(1), 41-55.
2. Austin, P. C. (2011). An introduction to propensity score methods for reducing the effects of confounding in observational studies. Multivariate Behavioral Research, 46(3), 399-424.
3. Stuart, E. A. (2010). Matching methods for causal inference: A review and a look forward. Statistical Science, 25(1), 1-21.