Meta-RL之Meta-Gradient Reinforcement Learning

这篇文章是用元学习算法去学习RL的超参数 η = { γ , λ } \eta=\{\gamma,\lambda\} η={γ,λ}。当然不仅限于这2个超参数，还可以是和回报相关的超参数。

本文的核心思想：我们之前接触过Meta-Learning参数的初始化(MAML、Reptile)以及Meta-Learning参数的更新优化(L2L-by-gd-by-gd、Opt as a model for few-shot learning)，那么这篇就是能否Meta-Learning到 η = { γ , λ } \eta=\{\gamma,\lambda\} η={γ,λ}这两个超参数。

这篇文章教会了我们如何去meta-learning超参数，为后续Meta-Learning的发展奠定了基础。可惜的是，作者并没有给出源码。

参考列表：
①Meta-RL系列论文简介
②元梯度强化学习算法
③IMPALA

Abstract

1. 对于强化学习而言，最重要的信息就是Agent收到的回报信息，因此作者主要想探究就是最优的回报形式是怎么样的，将回报看成是meta参数$\eta$的函数，然后用基于梯度的方式来优化、在线调整$\eta$，从而在智能体与环境的交互中，使得回报既能适应具体问题，又能随着时间动态调整以适应不断变化的学习环境。
2. 关于meta参数 η = { γ , λ } \eta=\{\gamma,\lambda\} η={γ,λ}，其中$\gamma$是折扣因子，$\lambda$是自举参数。
3. 作者将本文所产生的新算法在57个Atari游戏上进行实验，最后可以达到sota的表现。从而证明了元梯度强化学习算法可以适用于DRL任务。

1 Meta-Gradient Reinforcement Learning Algorithms

定义更新规则为$f(\tau ,\theta ,\eta )$，其中$\tau$为强化学习中的一条episode： τ t = { S t , A t , R t + 1 , ⋯ } \tau_t=\{S_t,A_t,R_{t+1,\cdots}\} τt​={St​,At​,Rt+1,⋯​}；$\theta$为值函数网络和策略网络的参数(其实个人觉得还是分开来说比较好，但是作者可能为了简便说明，统一用$\theta$表示)；$\eta$为meta参数。
Meta-Learning有2个角色：Meta-Learner和Learner，我们分别用$\theta$和${\theta }^{\prime }$表示，因此参考类似于MAML的做法，fast-weights的获得如下所示：
$${\theta }^{\prime }=\theta +f(\tau ,\theta ,\eta )\text{\hspace{1em}(1)}$$Note：

1. 更新规则$f(\cdot )$一般指代学习率$\alpha$和梯度$\nabla$的乘积。

那么式(1)是如何训练的呢？
作者提出主要是基于在线交叉验证(Sutton,1992)的方式：具体的，RL算法从参数$\theta$出发，在first-sample上进行训练，利用采样得到的经验以及式(1)获得fast-weights——${\theta }^{\prime }$；然后在subsequent-sample上对${\theta }^{\prime }$的表现进行评估验证，然后对参数$\eta$进行更新。整一套流程其实和监督学习里的交叉验证没啥区别。

1. First-sample就相当于Meta-Learning中的Support-set；Subsequent-sample就相当于Query-set。
2. 2个sample集是互相独立的，分别记为$\tau$和${\tau }^{\prime }$。
3. 训练目标和评价指标分别记为$J(\tau ,\theta ,\eta )$和$J^{\prime }({\tau }^{\prime },{\theta }^{\prime },{\eta }^{\prime })$。需要注意是RL中一般$J$都是回报函数，且由于本论文提出的是一种gradient-based算法，故$J$必须是可微分的，因此值函数的形式不宜采用定义式，而应该是policy-based形式。
4. ${\eta }^{\prime }$采用固定的值来做参考。

评估：
由Meta-Learning的评估函数对Meta-Learner参数的更新一般都是建立在Query-set上的：
$$\frac{\partial J^{\prime }({\tau }^{\prime },{\theta }^{\prime },{\eta }^{\prime })}{\partial \eta }=\frac{\partial J^{\prime }({\tau }^{\prime },{\theta }^{\prime },{\eta }^{\prime })}{\partial {\theta }^{\prime }}\cdot \frac{\mathrm{d}{\theta }^{\prime }}{\mathrm{d}\eta }\text{\hspace{1em}(2)}$$Note：

1. 由于我们现在是为了meta-learning参数$\eta$，而不是$\theta$，否则就成了MAML了，所以偏导的对象是我们的超参数 { γ , λ } \{\gamma,\lambda\} {γ,λ}。和MAML的还有一个区别是，MAML对于$\theta$的训练并不是online的(具体可查看MAML论文的Algorithm 3第十行，注意这里指的是online而不是on-policy)，而本文的元梯度算法对于$\eta$的训练是online的，即每一个step下，都会在线做出应有的调整。
2. $\frac{\mathrm{d}{\theta }^{\prime }}{\mathrm{d}\eta }$表明meta参数$\eta$对fast-weights的影响。

求出式(2)的关键在于求出$\frac{\mathrm{d}{\theta }^{\prime }}{\mathrm{d}\eta }$：
$$\begin{gathered} \frac{\mathrm{d}{\theta }^{\prime }}{\mathrm{d}\eta }=\frac{\mathrm{d}(\theta +f(\tau ,\theta ,\eta ))}{\mathrm{d}\eta }=\frac{\mathrm{d}\theta }{\mathrm{d}\eta }+\frac{\partial f(\tau ,\theta ,\eta )}{\partial \theta }\cdot \frac{\mathrm{d}\theta }{\mathrm{d}\eta }+\frac{\partial f(\tau ,\theta ,\eta )}{\partial \eta } \\ =(I+\frac{\partial f(\tau ,\theta ,\eta )}{\partial \theta })\frac{\mathrm{d}\theta }{\mathrm{d}\eta }+\frac{\partial f(\tau ,\theta ,\eta )}{\partial \eta }\text{\hspace{1em}(3)} \end{gathered}$$令
$$\begin{gathered} \mu =I+\frac{\partial f(\tau ,\theta ,\eta )}{\partial \theta } \\ {z}^{\prime }=\frac{\mathrm{d}{\theta }^{\prime }}{\mathrm{d}\eta } \\ z=\frac{\mathrm{d}\theta }{\mathrm{d}\eta } \end{gathered}$$则
$$z^{\prime }=\mu z+\frac{\partial f(\tau ,\theta ,\eta )}{\partial \eta }\text{\hspace{1em}(4)}$$
当选择让$\mu =0$的时候，意味着不用去求二阶偏导数了，求出了$\frac{\mathrm{d}{\theta }^{\prime }}{\mathrm{d}\eta }$之后，我们就可以使用SGD(Adma等)对$\eta$进行参数更新了：
$$\eta \leftarrow \eta +\Delta \eta ,\Delta \eta =-\beta \cdot \frac{\partial J^{\prime }({\tau }^{\prime },{\theta }^{\prime },{\eta }^{\prime })}{\partial {\theta }^{\prime }}{z}^{\prime }\text{\hspace{1em}(5)}$$Note：

1. $\Delta \eta$就是表示目标函数对参数的梯度。
2. 详细推导如下

1.1 Applying Meta-Gradient to Returns

接下来就要做一些直接结合RL的具体的公式，而不仅限于上面这些符号。
首先需要将回报$g_{\eta }({\tau }_t)$表示成以meta参数$\eta$为变量的函数的形式，根据我们在value-based系列中的知识，可以写成n-step或者$\lambda$-return的形式。
n-step：
$$g_{\eta }({\tau }_t)=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\cdots {\gamma }^{n-1}+{\gamma }^n{v}_{\theta }(s_{t+n})\text{\hspace{1em}(6)}$$$\lambda$-return：$$g_{\eta }({\tau }_t)=R_{t+1}+\gamma (1-\lambda )v_{\theta }(s_{t+1})+\gamma \lambda g_{\eta }({\tau }_{t+1})\text{\hspace{1em}(7)}$$

1.2 Meta-Gradient Prediction

预测其实就是求出估计出值函数的过程，不一定要最优，但是要尽量精确估计。本篇论文采用TD($\lambda$)来做预测。
对于值函数估计一般通过最小二乘损失来表示：$J(\tau ,\theta ,\eta )=\frac{1}{2}(g_{\eta }(\tau )-v_{\theta }(s){)}^2$，其对$\theta$的梯度为：
$$\frac{\partial J(\tau ,\theta ,\eta )}{\partial \theta }=(g_{\eta }(\tau )-v_{\theta }(s))\cdot \frac{\partial v_{\theta }(s)}{\partial \theta }\text{\hspace{1em}(8)}$$然后定义$f(\cdot )$：
$$f(\tau ,\theta ,\eta )=-\alpha \cdot \frac{\partial J(\tau ,\theta ,\eta )}{\partial \theta }\text{\hspace{1em}(9)}$$更新规则$f$我们需要借助SGD去求得，其中$\alpha$为学习率。很自然的，我们接下去一定会回到$\Delta \eta$上：
$$\frac{\partial f(\tau ,\theta ,\eta )}{\partial \eta }=-\alpha \frac{\partial g_{\eta }(\tau )}{\partial \eta }\cdot \frac{\partial v_{\theta }(s)}{\partial \theta }\text{\hspace{1em}(10)}$$预测的核心思想就是通过调整meta参数$\eta$来做到最精确的预测。接下来观察公式(5)和公式(10)，还差一部分：
$$\begin{gathered} J^{\prime }({\tau }^{\prime },{\theta }^{\prime },{\eta }^{\prime })=\frac{1}{2}(g_{{\eta }^{\prime }}({\tau }^{\prime })-v_{{\theta }^{\prime }}(s^{\prime }){)}^2 \\ \frac{\partial J^{\prime }({\tau }^{\prime },{\theta }^{\prime },{\eta }^{\prime })}{\partial {\theta }^{\prime }}=(g_{{\eta }^{\prime }}({\tau }^{\prime })-v_{{\theta }^{\prime }}(s^{\prime }))\cdot \frac{\partial v_{{\theta }^{\prime }}(s^{\prime })}{\partial {\theta }^{\prime }}\text{\hspace{1em}(11)} \end{gathered}$$Note：

1. 这里$s^{\prime }$不是下个状态的意思，而是指subsequent-sample上的状态。
2. 对于${\eta }^{\prime }$通常采用固定形式做reference，如 η ′ = { γ ′ = 1 , λ ′ = 1 } \eta'=\{\gamma'=1,\lambda'=1\} η′={γ′=1,λ′=1}。

总结一下预测的流程：

1. 首先在first-sample上使用公式(8)以及公式(10)去求得相关梯度。
2. 然后在subsequent-sample上使用公式(11)去求得相关梯度。
3. 最后使用公式(5)对$\eta$进行更新。

1.3 Meta-Gradient Control

规划的另一部分就是控制，说白了就是求最优值，通常我们称预测为策略评估，而控制则是策略提升。
RL常见的比如Q-Learning就是典型的控制算法。这里作者采用了policy-based系列算法中的A2C，这是一种将预测和控制结合在一个更新式子中的Actor-Critic算法，往往我们将策略梯度上述看成是policy-improvement的一种方式。

控制：
目标函数仍是值函数：
$$-\frac{\partial J(\tau ,\theta ,\eta )}{\partial \theta }=(g_{\eta }(\tau )-v_{\theta }(s))\frac{\partial \log {\pi }_{\theta }(a|s)}{\partial \theta }+b(g_{\eta }(\tau )-v_{\theta }(s))\frac{\partial v_{\theta }(s)}{\partial \theta }+c\frac{\partial H({\pi }_{\theta }(\cdot |s))}{\partial \theta }\text{\hspace{1em}(12)}$$Note：

1. 一共分为三部分：第一部分是控制目标；第二部分是预测目标(这里也是我不解的地方，个人认为没必要再做一次预测吧)；第三部分是熵，用于增加策略的随机性。
2. 参数$b,c$表示各个部分在目标函数中的占比。

和预测一样的流程，接下去就是求更新规则及其对meta参数的梯度：
$$\begin{gathered} f(\tau ,\theta ,\eta )=-\alpha \cdot \frac{\partial J(\tau ,\theta ,\eta )}{\partial \theta } \\ \frac{\partial f(\tau ,\theta ,\eta )}{\partial \eta }=\alpha \frac{\partial g_{\eta }(\tau )}{\partial \eta }[\frac{\partial \log {\pi }_{\theta }(a|s)}{\partial \theta }+b\frac{\partial v_{\theta }(s)}{\partial \theta }]\text{\hspace{1em}(13)} \end{gathered}$$Note：

1. 同样也是通过SGD去求得梯度值。

控制的核心思想就是通过调整meta参数$\eta$来最大化提升值函数。接下来观察公式(5)和公式(13)，还差一部分：
$$\frac{\partial J^{\prime }({\tau }^{\prime },{\theta }^{\prime },{\eta }^{\prime })}{\partial {\theta }^{\prime }}=(g_{{\eta }^{\prime }}({\tau }^{\prime })-v_{{\theta }^{\prime }}(s^{\prime }))\frac{\partial \log {\pi }_{{\theta }^{\prime }}(a|s)}{\partial {\theta }^{\prime }}\text{\hspace{1em}(14)}$$
总结一下控制的流程：

1. 首先在first-sample上使用A2C算法公式(12)以及公式(13)去求得相关梯度。
2. 然后在subsequent-sample上使用公式(14)去求得相关梯度。
3. 最后使用公式(5)对$\eta$进行更新。
4. 另外需要注意的是，控制和预测在文中用了一个字母$J$表示，但实际上是不一样的。

1.4 Conditioned Value and Policy Functions

这一节主要是将meta参数嵌入到值函数网络和策略网络中，从而来增加回报的稳定性，使得预测也更加准确，对于训练稳定性的增加很有帮助。
为何回报会不稳定呢？
因为我们meta参数是直接和回报挂钩的，而参数的更新是在线更新的。举个例子，比如你在$\gamma =0$的时候，有一个不错的回报，但是当$\gamma$更新到$\gamma =1$之后，你可能会发现接下来的回报值很低，一方面是之前的短视($\gamma =0$)行为造成的。另一方面，$\eta \in [0,1]$，直接输入网络的话，会造成一定的稀疏性，因此我们可以通过Embedding的方式去解决这个问题：
$$\begin{gathered} v_{\theta }^{\eta }(s)=v_{\theta }([s;e_{\eta }]) \\ {\pi }_{\theta }^{\eta }(s)={\pi }_{\theta }([s;e_{\eta }]) \\ {e}_{\eta }=W_{\eta }\eta \end{gathered}$$Note：

1. $e_{\eta }$是输入为$\eta$的嵌入层，PyTorch或者Tf都有方便的实现。
2. $[s;e_{\eta }]$表示输入维度的堆积合并。
3. $W_{\eta }$是嵌入矩阵参数。

1.5 Meta-Gradient Reinforcement Learning in Practice

这一节讲的是元梯度算法在实现过程中的一些注意点：

1. 为了提高计算效率，目标函数的计算最好是每隔n-step计算一次，n步之内只进行$Loss$的累加。
2. 采用mini-batch数量的tasks。
3. 同一份task可以重复利用2次。举个例子，比如$\tau$被用来做$\theta \to {\theta }^{\prime }$，然后${\tau }^{\prime }$用在$J^{\prime }$上做$\eta$的更新。那么作者表达的是接下去同样也可以用${\tau }^{\prime }$在$J$上做$\theta \to {\theta }^{\prime }$的更新，然后$\tau$用在$J^{\prime }$上做$\eta$的更新。这样同一份数据就得到了充分利用。这种做法也特别适合于Meta-Learning算法中样本少得特性。

2 Illustrative Examples

这一节主要展示meta参数 η = { γ , λ } \eta=\{\gamma,\lambda\} η={γ,λ}是如何meta-learned到的。
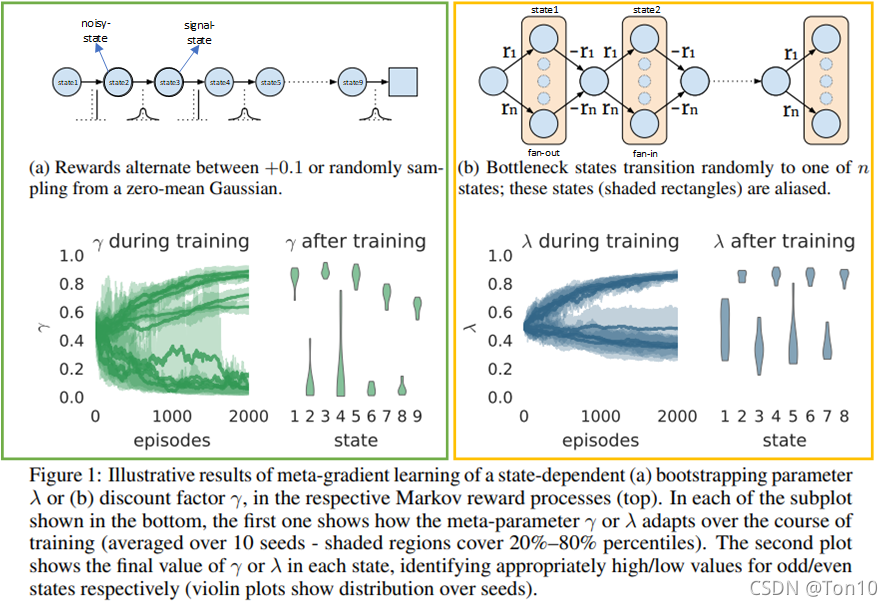如上图所示，左图是研究衰减系数$\gamma$，右图是研究自举参数$\lambda$。以左图为例，这是一个10步的MRP(指没有决策动作的MDP)，由2种状态交替组成。状态由信号状态与噪声状态组成，奖励有固定奖励$R=0.1$以及随机奖励$R\sim N(0,1)$两种。奇数编号的是信号状态，偶数编号的是噪声状态。
我们的目的是为了确保尽可能去获得较大的固定奖励0.1，而不要噪声奖励(噪声奖励大概率为0，而且还会有负奖励)，因此就需要Agent在信号状态的时候保持较高的$\gamma$，在噪声状态的时候保持较低的$\gamma$，训练结果如绿色框下方图所示，确实如我们分析的那样，奇数状态(signal-state)的$\gamma$很高，偶数状态(noise-state)的$\gamma$很低。
为什么元梯度算法的训练结果是这样呢？
首先我们要弄清楚$\gamma$的意义在于我们要Agent更加注重长远利益，而不仅仅是当下的高奖励，更重要的是，对于远处一些不好的、不确定的奖励进行衰减，以免让他们影响到近期的一些好的决策。
分析：
因为当你陷入噪声状态的时候，我们现在要考虑如何获取一个合适的$\gamma$，使得之后Agent获取好的奖励，Agent应该关注的是如何让当前的噪声奖励最大化，现在面临的情况是：下一个状态就是信号状态，这是我们想要的状态，但是由于下下个状态是噪声状态，因此最好加个衰减因子去衰减它，故$\gamma \to 0$是一个不错的更新方向；如上图所示，在噪声状态时候，训练时候的$\gamma$的值是很小的，之所以没有完全为0，也是Agent考虑到后续可能有好的状态。相反，当我们处于信号状态的时候，下个状态是噪声状态，下下个状态是信号状态，因此我们不怎么需要用衰减因子去衰减它，保持$\gamma$为一个比较高的值即可；如上图所示，在信号状态时候，经过训练的$gamma$接近于1，这样当下个状态来临，我们将这个$\gamma$用上，就会获得比较大的累计奖励，这也正是RL的总目标。

3 Deep Reinforcement Learning Experiments

3.1 Experiment Setup

这一节描述了一些实验的设置，比如环境ALE(应该是类似于Gym、rllab这类的)、网络、超参数(附录A中)等等

3.2 Experiment Results

实验原理也很简单，就是通过控制变量来研究元梯度算法的性能以及不同${\gamma }^{\prime }$下对于原梯度算法性能的影响，实验结果如下所示：
Conclusion：

1. 手动调节参数的算法IMPALA相比于自动调节参数的Meta-gradient算法相比，性能上总是差了许多，特别是对于$\gamma$的学习尤其明显。
2. 第一张图是在Atari游戏上只meta-learned衰减因子的相对表现结果：第二张图是meta-learned衰减因子和自举参数的相对结果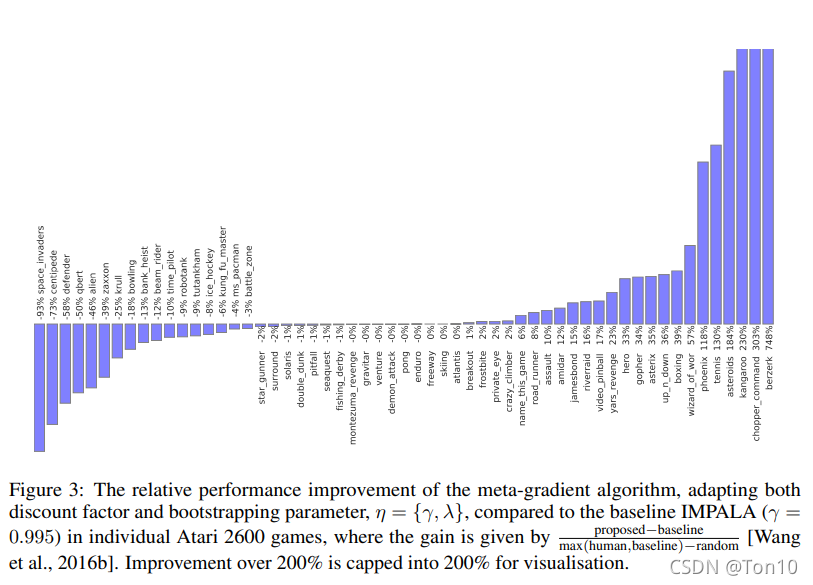：从结果来看，右半部分表示元梯度算法强于IMPALA，而两张图在这方面占据优势的游戏较多，且领先baseline较多。
3. 此外作者还对embedding层(第1.4节)的加入对元梯度算法的影响做了对比试验，实验结果来看，有embedding比无embedding效果提升许多，以此证明了将meta参数加入到策略网络和值函数网络的重要性。
4. 另外附录的最后一部分展示了上述训练过程的曲线图，有兴趣的读者可以去看看。

总结

1. 这篇论文告诉我们如何通过调整超参数去获取好的回报。Agent一边和环境进行交流，另一边调整meta参数$\eta$。实验结果也证明，自动调节的超参数比手动设计的超参数拥有更好地表现，甚至在Atari游戏上达到了sota！
2. 元梯度算法其实不仅仅适用于自举参数和衰减参数，你也可以设计其他和回报相关的超参数，使之拥有自动调节的能力，甚至可以设计到优化过程中的学习率或者是搜索方向。
3. 文章最大的意义在于解决了RL面临的一大棘手问题，就是超参数的选择，手动选择超参数一直被人诟病，而元梯度算法提出的自动调节无疑是作为解决这个问题的一个通用性好方向。