最短路径

最短路径除了用深搜和广搜之外，还有其他更优秀的算法

广搜http://blog.csdn.net/maxlykos/article/details/73650445 第四题

深搜http://blog.csdn.net/maxlykos/article/details/73555329 第八题

一.弗洛伊德算法

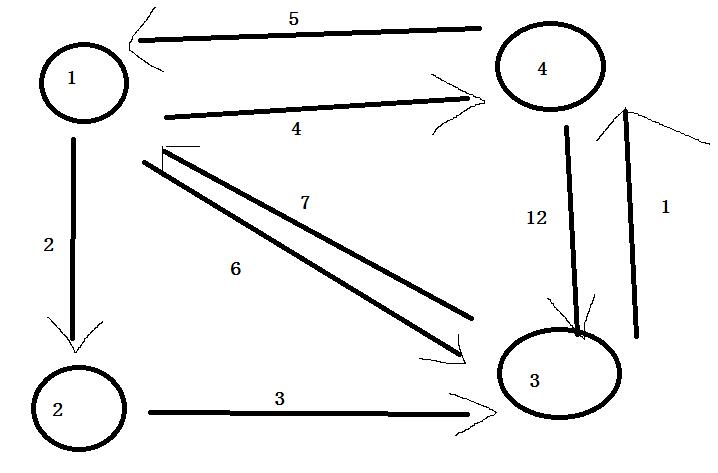
对于这样的一张图

可以构造邻接矩阵为

   1  2   3   4

1   0  2   6   4

2  ∞    0      3      ∞

3   7  ∞      0      1

4   5  ∞      12     0

该算法的基本思想是

假设求从顶点vi到vj的最短路径。如果从vi到vj有弧，则从vi到vj存在一条长度为arcs[i][j]的路径，该路径不一定是最短路径，尚需进行n次试探。首先考虑路径(vi, v0, vj)是否存在(即判别弧(vi ,v0)和(v0 , vj)是否存在)。如果存在，则比较(vi , vj)和(vi, v0, vj)的路径长度取长度较短者为从vi，到vj的中间顶点的序号不大于0的最短路径。假如在路径上再增加一个顶点v1，也就是说，如果(vi，…，v1)和(v1，…，vj)分别是当前找到的中间顶点的序号不大于0的最短路径，那么(vi，…，v1，…，vj)就有可能是从vi到vj的中间顶点的序号不大于1的最短路径。将它和已经得到的从vi到vj中间顶点序号不大于0的最短路径相比较，从中选出中间顶点的序号不大于1的最短路径之后，再增加一个顶点v2，继续进行试探。依次类推。

简单的说，就是最开始只允许经过1号顶点进行中转，然后全图遍历，接下来只允许经过1和2号顶点进行中转.....允许1到n号所有顶点进行中转，求任意两点之间的最短路径。

什么意思呢？从这个图上讲，假如我们只看2到1，一开始2到1是无穷大，然后引入点1，判断if(map[2][1]+map[1][1]<map[2][1]){map[2][1]=map[2][1]+map[1][1];}/*更新最短路径*/,发现不成立，所以2到1仍然是无穷大，然后引入点2,判断if(map[2][2]+map[2][1]<map[2][1]){map[2][1]=map[2][2]+map[2][1];}，仍然不成立，所以2到1仍然是无穷大，然后引入点3，继续判断，发现成立，所以更新2到1的权值为map[2][3]+map[3][1]=10，注意下此时2到4的权值也更新为了4（2到3到4），然后引入点4，判断发现[2][4](也就是2到3到4)+[4][1]=9<刚才的10，所以最后2到1的最短路径为9

其他的情况类似

整个算法的核心代码只有5行

	for (int k = 1;k <= 4;k++)  //引入第k个顶点
		for (int i = 1;i <= 4;i++)
			for (int j = 1;j <= 4;j++)
				if (map[i][k] + map[k][j] < map[i][j])
					map[i][j] = map[i][k] + map[k][j];

i和j用来实现多源，即所有顶点全部都遍历一遍
代码

#include "stdafx.h"   
#include "iostream"  
using namespace std;
void main()
{
	int map[5][5] = { 0 };
	for (int i = 1;i <= 4;i++)
		for (int j = 1;j <= 4;j++)
			if (i == j)map[i][j] = 0;
			else map[i][j] = 99999999;

    map[1][2] = 2;
	map[1][3] = 6;
	map[1][4] = 4;
	map[2][3] = 3;
	map[3][1] = 7;
	map[3][4] = 1;
	map[4][1] = 5;
	map[4][3] = 12;

	for (int k = 1;k <= 4;k++)
		for (int i = 1;i <= 4;i++)
			for (int j = 1;j <= 4;j++)
				if (map[i][k] + map[k][j] < map[i][j])
					map[i][j] = map[i][k] + map[k][j];
	for (int i = 1;i <= 4;i++)
	{
		for (int j = 1;j <= 4;j++)
			printf_s("%5d", map[i][j]);
		cout <<endl;
	}
}

这个算法可以处理带负权边，但不能处理负权回路

二.迪杰斯特拉算法

单源最短路

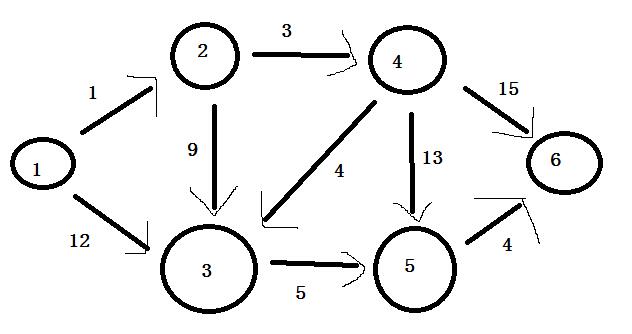
如图所示，建立邻接矩阵

   1  2  3  4  5  6

1   0  1  12 ∞   ∞    ∞

2  ∞     0    9    3    ∞    ∞

3  ∞     ∞   0    ∞     5    ∞

4  ∞     ∞   4     0    13  15

5  ∞     ∞   ∞    ∞     0    4

6  ∞     ∞   ∞    ∞     ∞    0

求1号顶点到其他顶点的最短路径

还需要用一个一维数组distance[]来存储1号顶点到其余各个顶点的初始路程

distance[]= {0  0  1  12  ∞    ∞    ∞};

           1  2  3   4   5   6

接着对原点不断的进行松弛操作，所谓松弛操作，就是对一个顶点设置一个属性用来描述该顶点到其他顶点权值的上界，也就是一个估计的最大距离，也就是一个估计值，然后通过判断其他的点“绕路”来不断的降低这个距离，直到降低为确定值

具体流程如下，假如从顶点1出发，查看顶点1的属性distance数组，发现该点到顶点2的距离最短，所以distance[2]就从估计值变为了确定值，不需要再松弛，因为图中没有负权值，所以在直达是最短的前提之下再去找路肯定距离更远，所以distance[2]变成了确定值，然后从点2出发，首先发现点2有2到3和2到4两个出边，先判断2到3这个出边，对distance[3]进行松弛，，判断1->2->3是否比1->3更短，也就是distance[3]>distance[2]+map[2][3]?，结果发现1->2->3距离小于1->3，所以更新distance[3]，从12改成1+9=10，再判断2到4这个出边，对distance[4]进行松弛，判断1->2->4是否比1->4更短，也就是distance[4]>distance[2]+map[2][4]将distance[4]松弛为4。到此时，点2的所有出边都松弛完了。然后把2忽略掉，从3，4，5，6中通过上一步松弛2得到的distance数组选一个距离1最近的，是4，因为之前已经将2松弛完了，所以这里可以看作distance数组仍是点1到其他顶点直达的距离（跟一开始得到的distance性质一样），又因为distance[4]是最小的，而且绕路只会增大权值，所以可以看作1->4是直达且距离最短的，也就是一开始1到2的情况，也就是说，distance[4]已经变成了确定值。

说的可能很繁琐，总结一下上面的操作，首先一开始的distance全部是直达权值，直达不了的就是无限大，然后找一个到1最近的，不需要再松弛的，也就是2，然后默认1到2的连通的点时必须经过2，然后松弛2，也就是找到1到3和4的最短路径到底需不需要经过2，更新distance，松弛完2，就看作1到其他所有顶点的权值仍为直达权值并把点2默认忽略掉（2的权值已经加入到distance里的，所以不用再管他），依照一开始确定不需要再松弛的点的方法找到点4，然后默认1到4连通的点必须经过4，然后松弛4，看看1到3，5，6的最短路径到底需不需要经过4，并更新distance，4松弛完毕后，就看作1到其他顶点的权值仍为直达权值，并把2，4省略掉，再从distance的2,5,6中找到一个确定值，依次类推，当distance中的全部都变成确定值时，distance就是1号顶点到其他顶点的最短路径了

算法怎么用代码处理呢，可以这样

 1.为了方便区分确定值和估计值，我们将所有顶点分为两部分，确定值和估计值，一开始，确定值中只有顶点2，怎么区分？用一个一维bool数组就可以了,bool book[]，book[2]代表2为确定值，否则为估计值

 2.设置源点1到自己的最短路径为0，即distance[1]=0，查找源点可以直达的顶点，并把相应的distance设置为对应距离，其他的设为无穷大，到这一步这就算是初始化了

 3.在book中为0的点中查找一个权值最小的顶点，把他的book设为1，并遍历该点所直接连接的顶点，判断源点直达该点和源点从之前设为确定值的点绕路去该点谁权值更小，并将distance更新为更小的那个

 4.重复步骤3，终止条件为步骤三重复了n-1次，n为点总数

上代码

#include "stdafx.h"   
#include "iostream"  
using namespace std;
void main()
{
	int map[7][7] = { 0 };
	for (int i = 1;i <= 6;i++)
		for (int j = 1;j <= 6;j++)
		{
			if (i == j)
				map[i][j] = 0;
			else 
				map[i][j] = 999999;
		}

	map[1][2] = 1;
	map[1][3] = 12;
	map[2][3] = 9;
	map[2][4] = 3;
	map[3][5] = 5;
	map[4][3] = 4;
	map[4][5] = 13;
	map[4][6] = 15;
	map[5][6] = 4;

	bool book[7] = { 0 };
	book[1] = true;
	int distance[7] = { 0 };
	for (int i = 1;i <= 6;i++)
		distance[i] = map[1][i];//步骤1和2完成

	//迪杰斯特拉算法，步骤3
	for (int i = 1;i <= 5;i++)  //终止条件为步骤3执行了n-1次
	{
		//找到源点直达的最小值，并确定为确定值
		int min = 999999,t;
		for (int j = 1;j <= 6;j++)
		{
			if (book[j] == 0 && distance[j] < min)
			{
				min = distance[j];
				t = j;
			}
		}
		book[t] = true;//这就算是将源点到点t权值的最小值设置为确定值了
		//下面是判断源点到确定值点所直达的点的权值最小值是否需要通过确定值点
		for (int k = 1;k <= 6;k++)
		{
			if (map[t][k] < 999999)  //确定值可以直达
			{
				if (distance[k] > distance[t] + map[t][k])  //判断是否需要绕路
				{
					distance[k] = distance[t] + map[t][k];
				}
			}
		}
	}
	for (int i = 1;i <= 6;i++)
		cout << distance[i] << endl;
}

个人感觉这个算法中将某个点从估计值判断为确定值这个地方就很符合分治，通过松弛来约定一个实际上跟源点不直达的点可以“直达”。我以后再慢慢领悟