Games101-光线追踪（蒙特卡洛积分与路径追踪）

最新推荐文章于 2024-08-23 16:46:09 发布

Mhypnos

最新推荐文章于 2024-08-23 16:46:09 发布

阅读量1.1k

点赞数 13

分类专栏： Games101 图形学文章标签：图形学 games101 笔记

本文链接：https://blog.csdn.net/Mhypnos/article/details/137872469

版权

图形学同时被 2 个专栏收录

51 篇文章

订阅专栏

Games101

22 篇文章

订阅专栏

本文介绍了渲染方程和蒙特卡洛积分在计算视觉中的应用，特别是路径追踪算法，探讨了如何通过随机采样解决直接光照和漫反射问题。文章还讨论了Whitted-style光追的局限性以及如何改进采样策略，包括使用多线程和重要性采样来提高渲染效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Reivew

在这里插入图片描述
渲染方程：看到的某点颜色等于自身发射的光，加上从四面八方反射的光

渲染里更多考虑连续性随机变量
随机变量x符合某一种概率密度分布f(x)
概率密度函数：非负，积分为1.
期望：值乘以概率密度加起来(或者积分)

Monte Carlo Integration/蒙特卡洛积分

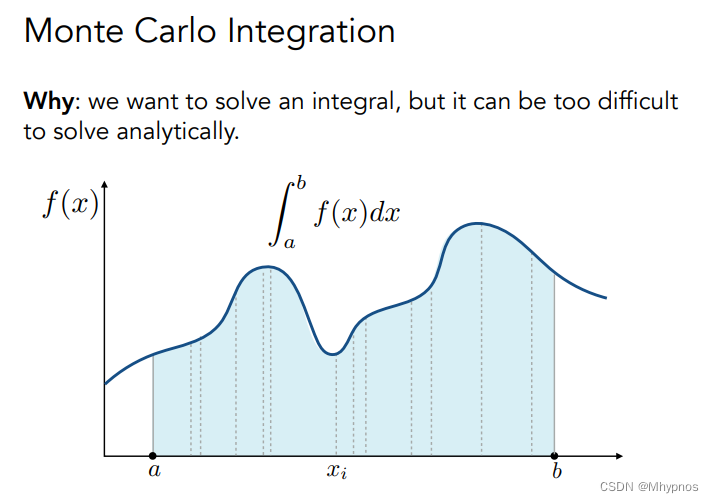
在这里插入图片描述
蒙特卡洛是为了解定积分：从a~b函数下面围的面积

在ab之间随机取一个数 $x_i$ ，得到对应的 $f(x_i)$ 。假设整个曲线是要给长方形，长方形高为 $f(x_i)$ ，宽度为 $ab$ ，在ab间重复多次采样，将每次得到的长方形平均即为结果
在这里插入图片描述
在积分域 $ab$ 间随机采样一个位置，可以定义任何一个概率密度来采样，采样出位置 $x_i$ ，蒙特卡洛表示积分可以近似成 ${f(x)}\over{p(x)}$ 的求和平均

例子：假设在ab间均匀采样，则采样用的PDF各处相同，是个常数C
在这里插入图片描述
根据蒙特卡洛积分随机采样，采样得到 $x_i$ ，对应的 $p (x)$ 为 ${1}\over{b-a}$
得到的结果就是之前的定义：随便取一个x，找到高度，乘以b-a，得到一个矩形，再把所有采样的矩形求平均

不管如何采样，只要有一个满足的PDF，求可以求到定积分的近似

只需要能够在ab间以一种方式进行采样，只要知道采样对应的PDF就可求积分。不用关心积分域是多少，因为积分域已经在PDF里体现出来了

性质：

采样数越多，方差越小，得到的结果越准
对x采样，对x积分

Path Tracing/路径追踪

在这里插入图片描述
Whitted-style光线追踪两种情况：
当一个光线打到光滑的物体，会沿着镜面方向反射，或者折射方向折射
当光线打到打到漫反射的物体，就停了

问题1：左边更像镜子specular，右边稍微有点糊glossy(光滑，但不完全光滑)
Whitted-style光追只对左边有用，因为glossy看上去是糊的，不能说光线也沿着specular的方向走，即镜面反射是不对的
在这里插入图片描述
Whitted-style光追打到diffuse物体就停了，然后直接做shading，但实际上物体会把光线反射到不同的方向上。因此就考虑不到漫反射物体和漫反射物体之间的光线
如上图：光源在上方，光线往下大的，如果是直接光照，天花板是黑的，以及长方体左侧的面也是黑的。但是全局光照里，都是可以看到的。红墙旁边的立方体侧面会被照成有些红色
在这里插入图片描述
Whitted-style光追是错的，但是渲染方程是精确的

渲染方程解积分
先考虑简单情况，考虑一个点的直接光照。着色的到摄像机的方向 $\omega_o$ ， $\omega_i$ 各个不同的入射方向
(虽然实际光线是从光源到物体，但这里的考虑都是从着色点出发往外)
在这里插入图片描述
忽略渲染方程里的自发光项。
直接光照说明 $L_i$ 只有可能是光源自己带的，否则为0
根据蒙特卡洛积分在各个方向随机采样，对应的 $f (x)$ 和PDF就是需要求的量

最简单的采样即均匀的采样 ${1}\over{2\pi}$ ，球面的面积是4Π，则半球面面积是2Π，所以半球对应的立体角为2Π
在这里插入图片描述
从式子可以看出任何一个着色点，出射的radiance是多少

直接光照到这一步就求出结果了

从观察点看到p点的光，可以是任何一个方向的radiance，不一定是光源还是反射的，不作区别。所以从Q点到P点的radiance，可以认为Q点也是一个光源，照亮P点。
因此从Q点到P点反射多少radiance，可以类比为在P点观察Q点，算Q的直接光照
即上图的摄像机看Q点反射到P点的radiance，相当于在Q点算出的直接光照
在这里插入图片描述
如果打到的是光源，直接计算，如果打到的是物体，考虑这个物体对应Q点，反射过来的radiance是多少，也就是在Q点的直接光照，在Q点以 $-\omega_i$ 方向看过去的直接光照

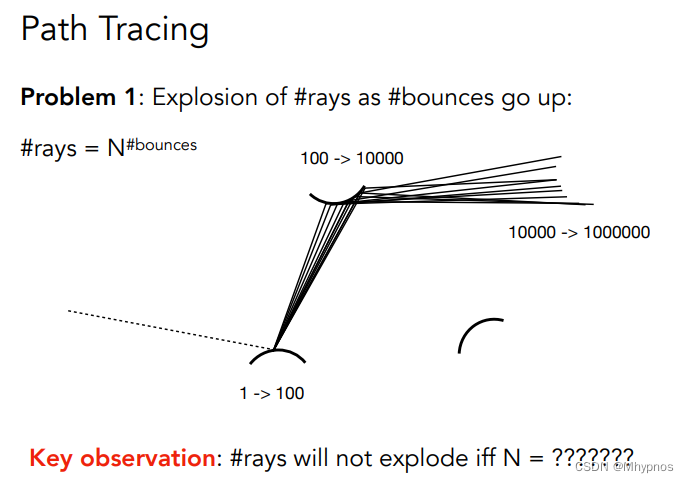
问题1：以这种方式打出各种光线，递归的来算，光线的数量会爆炸

只有N等于1是，指数才不会爆炸。
因此在任何一个点着色点只打出一条光线，N即为蒙特卡洛中采样的次数，没有规定N需要多大，只不过N大是噪声小，N小是噪声大。但都符合蒙特卡洛积分
在这里插入图片描述
因此只用一根光线求解问题，对任何一个点做着色，不用for循环，随机往一个方向采样

N=1做蒙特卡洛积分即为路径追踪
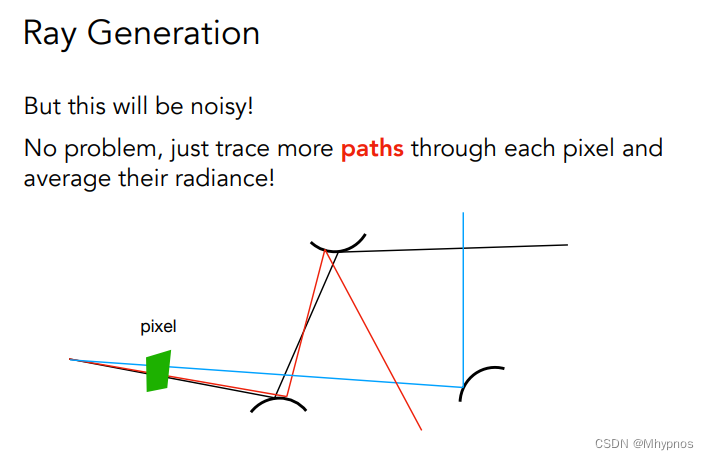
在这里插入图片描述
穿过一个像素可以有很多不同的路径，只要用足够多的path求平均即可

在像素内，均匀/随机的取n个不同的位置，对于任何一个选取的位置，从视点/摄像机位置，连一根光线到样本的位置上，形成一道光线，如果打到了物体的位置，就要算着色
这里其实也是蒙特卡洛积分
在这里插入图片描述
问题2：递归无法停止

如果限制光只能弹射3次

弹射17次。
如果提前把光的弹射次数限制在某一范围是不对的，因为损失了能量，多次弹射损失的能量没有考虑。
真实情况光就是弹射无数次

用俄罗斯轮盘赌的方式，来决定一定概率去停止继续往下追踪
在这里插入图片描述
设我们所求的某一个着色点出射的radiance结果为 $L_o$ ，提前定义一个概率 $P$ ，以这个概率 $P$ 往某个方向打一光线，最后得到一定的结果后，除以概率 $P$ ，以另外的概率 $1 - P$ ，不打这条光线，得到的结果即为0.
仍然可以期望最后的结果是 $L_o$ ，因为这里仍然是离散型随机变量的期望。
结果仍然是对的，只不过有噪声
在这里插入图片描述
首先随机在0-1里随机取一个数，如果大于P_RR，则返回0

现在的路径追踪算法是正确的，但是不高效

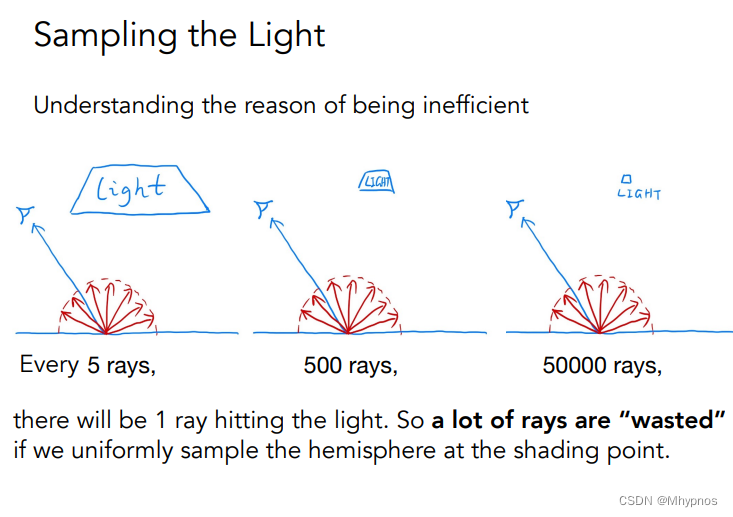
光源有大有小，对于大光源，可能打5根光线，就能打到光源，对于非常小的光源，可能要打5万根光源。
说明随机打出的光线能否打到光源是看运气的。
有很多光源可能被浪费掉，因为在着色点，是均匀的往四面八方去采样。
在这里插入图片描述
如果直接在光源上采样，那所有的采样样本都不会浪费。
对于着色点，不在往四面八方采样，直接在光源上进行采样，光源本身有一个朝向 $\vec n^,$ 。可以和着色点连线，与着色点法线 $\vec n$ 夹角 $\theta$ ，与光源法线夹角 $\theta^,$
光源是个框，面积为 $A$ ，在二维平面上均匀采样，pdf为 ${1}\over{A}$
蒙特卡洛要求积分在一个积分域上，现在采样是在光源上采样，但是积分是在立体角上积分，所以需要把渲染方程写成在光源上的积分
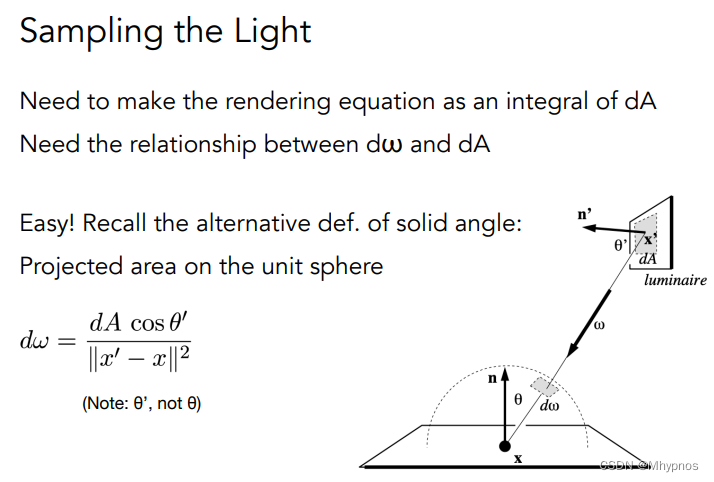
在这里插入图片描述
只需要知道 $d\omega$ 和 $d A$ 的关系， $d\omega$ 相当于 $d A$ 投影到单位球上的立体角
立体角相当于面积除以距离平方，也可以理解为把一个面积投影到单位球的表面上，因为单位球半径是1

先把 $d A$ 扭转过来，求出正面面对着色点的投影面积 $dA*cos\theta^,$
在这里插入图片描述
渲染方程重写为 $d A$ 的形式

根据新的渲染方程，直接对光源进行采样。
着色的结果分为两部分：1是来自光源的贡献，直接对光源采样，这部分不需要俄罗斯轮盘赌，因为是直接光照。2是对来自非光源的贡献，仍然用原来的方法
在这里插入图片描述

判断光源能否直接对着色点做出贡献，即有无阻挡。
考虑着色点到光源采样点取一连线，看中间有无打到其他物体

路径追踪是比较困难的事情

path tracing几乎是百分百正确的算法

早期的光学追踪，更多指Whitted-style光追
现代的光学追踪，理解成所有光线传播方法的大集合：(单向/双向)路径追踪、光子映射、Metropolis光线传输…
现在生成一张图，要么光栅化，要么光线追踪，但不是早期的Whitted-style光追
在这里插入图片描述
如何对一个半球进行均匀采样？
给任何一个函数，如何采样？
蒙特卡洛积分可以用在任意pdf，选择什么样的pdf是最好的？(重要性采样理论，如何针对某一种形状的函数进行最好的采样方法)
如何选择随机数？low discrepancy sequences随机数序列
在这里插入图片描述
可以采样半球，也可以采样光源，结合两种，使得效果更好。multiple imp. sampling
对一个像素打出不同得路径，为什么平均起来就是像素得radiance？pixel reconstruction filter
一个像素里的radiance和最后的颜色不是线性对应的，如何转化？
路径追踪仍然是Introductory

作业

最早实现的效果右边整个都是黑的
在这里插入图片描述
后来找网上看别人的分析，发现是右边的绿色墙的包围盒不是个立方体，而是个四边形，只是一个面，其实就是一个轴的tEnter与tExit是相等的
而我之前的包围盒相交判断 Bounds3::IntersectP里

tEnter < tExit

绿色墙壁会被判断为不相交
所以要改成

tEnter <= tExit

在这里插入图片描述
有很多黑噪点，按提示应该是浮点数精度问题
判断直接光照是否有阻挡加个偏移

发现没有光源区域虽然不是纯黑，但是也没有显示，因为伪代码里处理的着色点都是物体反射到摄像机的光，还需要处理着色点就是光源得情况，直接显示光源色就行

if (intersection.obj->hasEmit()) {
	return intersection.emit;
}

在这里插入图片描述
改回采样16

多线程

尝试对每个像素的采样分别进行多线程处理，最终大概块了3倍时间，cpu的调用率显示也接近是3倍

for (int k = 0; k < spp; k++){
	framebuffer[m] += scene.castRay(Ray(eye_pos, dir), 0) / spp;  
}

改成

std::future<Vector3f> fut[16];
for (int k = 0; k < spp; k++){
	fut[k] = std::async(std::launch::async, [&](Ray ray, int depth) {
		return scene.castRay(ray, depth);
	}, Ray(eye_pos, dir), 0);
}
for (int k = 0; k < spp; k++) {
	framebuffer[m] += fut[k].get() / spp;
}

在这里插入图片描述

在这里插入图片描述

尝试将屏幕分成多段，通过多线程分别处理

std::thread th[16];
    int thHeight = scene.height / 16;
    auto renderFunc = [&](int startH, int endH) {
        int m = startH * scene.width;
        for (uint32_t j = startH; j < endH; ++j) {
            for (uint32_t i = 0; i < scene.width; ++i) {
                // generate primary ray direction
                float x = (2 * (i + 0.5) / (float)scene.width - 1) *
                    imageAspectRatio * scale;
                float y = (1 - 2 * (j + 0.5) / (float)scene.height) * scale;

                Vector3f dir = normalize(Vector3f(-x, y, 1));
                for (int k = 0; k < spp; k++) {
                    framebuffer[m] += scene.castRay(Ray(eye_pos, dir), 0) / spp;
                }
                m++;
            }
            mtx.lock();
            progress++;
            UpdateProgress(progress / (float)scene.height);
            mtx.unlock();
        }
    };
    for (int i = 0; i < 16; i++) {
        th[i] = std::thread(renderFunc, i * thHeight, (i + 1) * thHeight);
    }
    for (auto& t : th) {
        t.join();
    }