GNN携手强化学习！刷爆顶会SOTA，霸榜的28个顶会方案！

图神经网络（GNN）与强化学习（RL）的结合，是一个充满活力的研究领域，它融合了GNN在图数据表示上的深度学习能力和RL在决策过程中的策略优化能力。这种结合为处理具有复杂图结构的数据问题提供了强大的工具。GNN能够深入挖掘图中的模式和关系，而RL则擅长在动态环境中进行序列决策，尤其是在需要长期规划和适应环境变化的情况下。通过将两者结合起来，可以开发出能够同时学习图结构表示和做出最优决策的智能模型。

GNN与强化学习的结合不仅推动了图机器学习的研究进展，还促进了新算法和模型的创新，为解决现实世界中的复杂问题开辟了新途径。近年来，众多研究者在这一领域进行了深入探索，产出了丰富的学术成果。

为了帮助研究者们系统地了解【GNN+强化学习】领域的最新进展，并激发新的研究思路，我们精心整理了过去两年中该领域的28篇重要研究成果。这些成果涵盖了论文、研究来源以及相应的代码资源，旨在为学术探索提供全面的参考和启发。希望通过这些资料，能够助力各位在【GNN+强化学习】领域的研究旅程中取得新的突破。

三篇论文详解

1、When GDD meets GNN: A Knowledge-driven Neural Connection for Effective Entity Resolution in Property Graphs

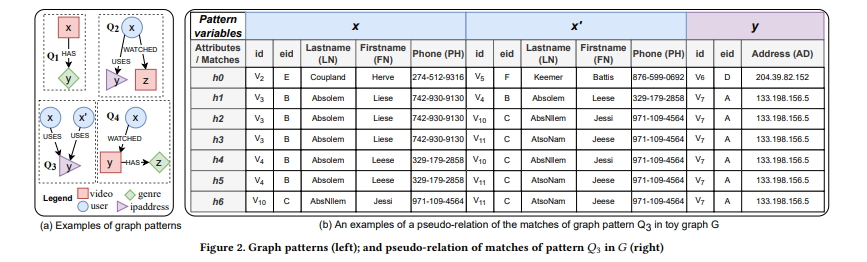
这篇文章提出了一个针对属性图实体解析（Entity Resolution, ER）的混合解决方案，称为GraphER。该方案结合了基于图的差异依赖（Graph Differential Dependency, GDD）和图神经网络（Graph Neural Network, GNN）的优势，旨在提高实体解析的效率和可解释性。

研究方法：

文章首先介绍了实体解析的重要性，尤其是在数据整合和清洗中。实体解析任务的目标是识别并链接指向相同现实世界实体的不同记录。作者指出，现有的解决方案主要分为基于规则的方法和基于学习的方法，它们各有优缺点。基于规则的方法易于解释且能够编码领域知识，而基于学习的方法虽然有效，但通常缺乏透明度。

为了克服这些限制，作者提出了GraphER框架，它包含以下几个关键步骤：

• 向量化输入图：通过元路径引导的随机游走和属性编码器-解码器神经网络，学习结构和属性信息。

• 生成候选匹配对：使用局部敏感哈希（LSH）技术生成候选匹配对，形成块。

• 剪枝：通过计算边权重和使用Dice系数来减少块中的误匹配对。

• 匹配确定：使用GDD规则来确定实体对是否指向相同的真实世界实体。

创新点：

• 知识驱动的神经连接：文章的主要创新在于将GDD用于编码记录匹配规则，并用这些规则指导基于GNN的表示学习。这种结合了规则和学习的方法旨在利用两者的优势。

• 混合ER解决方案：提出了一种新颖的框架，使用结构和属性信息的GDD来明确帮助输入属性图的向量化。

• GDD的语义匹配规则：文章展示了如何使用GDD来发现样本 eid-标记的属性图中的语义匹配规则。

实验结果：

尽管实验结果证实了GraphER在处理图数据时的有效性，并且与最先进的技术相比具有竞争力，但这些结果本身并不构成创新点。文章的实验部分包括在17个图数据集和7个关系数据集上的广泛评估，并与10种最先进的技术进行了比较。

实验验证：

实验验证了GraphER在不同类型数据集上的性能，包括具有不同噪声水平的数据集。此外，文章还通过消融研究来评估GraphER框架中不同组件的影响，证明了结构信息和属性信息在实体解析中的重要性。

总的来说，这篇文章通过提出一种结合了规则和深度学习的方法，为属性图的实体解析问题提供了新的视角。通过利用GDD规则和GNN，GraphER不仅提高了实体解析任务的准确性，还增强了模型的可解释性。

2、PHYSICS-INFORMED GNN FOR NON-LINEAR CON-STRAINED OPTIMIZATION: PINCO A SOLVER FOR THE AC-OPTIMAL POWER FLOW

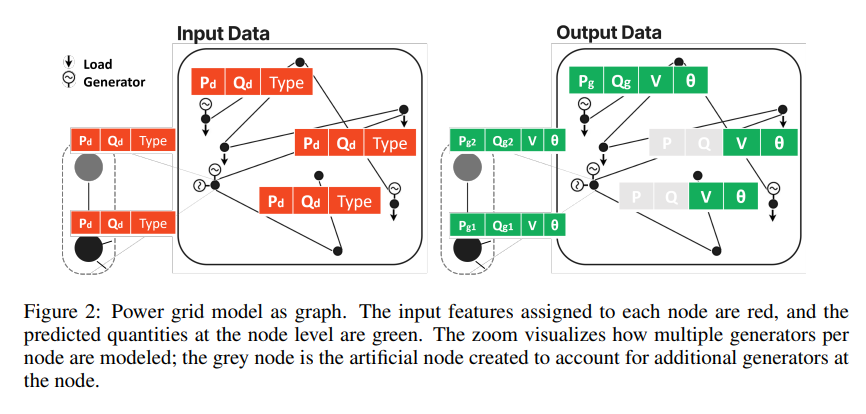
这篇文章介绍了一种基于物理信息的图神经网络（Physics-Informed Graph Neural Network, PINCO）方法，用于解决非线性约束优化问题：交流最优功率流（AC-OPF）。AC-OPF是电力系统中的一个关键优化问题，它需要在满足系统物理约束的前提下，最小化发电成本。

研究方法：

文章首先介绍了最优功率流（OPF）问题的背景和重要性。OPF问题的目标是在满足电力系统物理约束（如功率平衡、电压和频率限制）的同时，最小化发电成本。传统的解决方法包括使用线性化的直流功率流模型（DC-OPF）或非线性规划方法（如内点法）。然而，这些方法在大规模系统中面临计算负担和可扩展性挑战。

为了克服这些挑战，文章提出了一种结合图神经网络（GNN）和物理信息神经网络（PINN）的方法。这种方法的核心是利用GNN处理电力系统的非欧几里得数据结构，并使用物理信息来指导神经网络的训练，从而减少对标记数据的需求。

创新点：

• 物理信息图神经网络（PINCO）：文章提出了一种新的AC-OPF解决方案，该方案结合了GNN和PINN的优势。这种方法不仅能够处理电力系统的复杂拓扑结构，而且能够利用物理法则来提高解的准确性和泛化能力。

• 硬约束优化：文章中的方法能够解决具有硬约束的优化问题，这是通过引入物理信息神经网络与硬约束（hPINNs）的概念来实现的。这种方法使用惩罚方法和增广拉格朗日方法来优化目标函数，同时满足等式和不等式约束。

• 无需标记数据的端到端训练：PINCO方法不需要标记数据，可以端到端地解决AC-OPF问题，这与传统的监督学习方法不同。

实验结果：

文章通过在IEEE标准测试系统（包括9、24、30和118节点系统）上的实验验证了PINCO方法的有效性。实验结果表明，PINCO在保持硬约束不违反的同时，能够以比传统非线性规划求解器更快的速度提供可行解。

实验验证：

实验部分展示了PINCO在不同负载条件下的性能，包括作为单一负载条件下的求解器和作为在多个负载条件下的通用函数逼近器。在单一负载条件下，PINCO生成的解与传统求解器（如MIPS）生成的解相当，并且在某些情况下，PINCO在减少等式约束违反方面表现更好。在多个负载条件下，PINCO作为通用函数逼近器的性能略有下降，但与MIPS求解器相比，其成本差异很小，且推理速度快两个数量级。

结论：

文章得出的结论是，PINCO方法在解决AC-OPF问题方面具有潜力，它不仅能够作为求解器产生与传统方法相当的解，而且能够作为通用函数逼近器泛化到未见过的负载条件。此外，PINCO在推理阶段的速度优势使其成为一个有吸引力的替代方案。未来的工作将集中在将该方法扩展到更大规模的电网，并解决N-1 AC-OPF问题。

3、Unveiling the Impact of Local Homophily on GNN Fairness: In-Depth Analysis and New Benchmarks

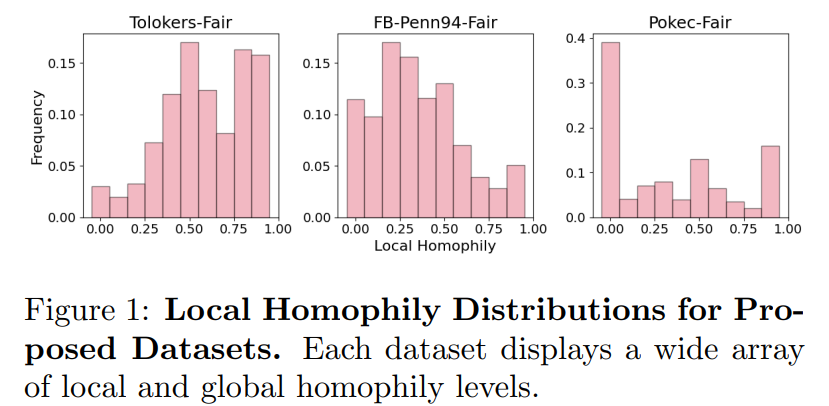
这篇文章探讨了图神经网络（GNNs）在处理具有同质性和异质性（homophily 和 heterophily）的图数据时的公平性问题。文章的核心观点是，GNNs在面对局部同质性水平与全局同质性水平差异显著的节点时，性能往往不佳。这种情况在以用户为中心的应用中尤为突出，这些应用中可能存在代表性不足的同质性水平。文章进一步探讨了局部同质性与GNNs公平性之间的联系，这是一个之前未被充分研究的领域。

研究方法：

文章首先提出了一个理论分析框架，用于评估在局部同质性水平在训练集和测试集之间存在差异时，GNNs预测的公平性。作者通过形式化定义了局部同质性水平的“非分布”（Out-of-Distribution, OOD）问题，并探讨了当局部同质性水平与训练数据集不同时，如何影响不同敏感属性节点的预测结果。

创新点：

• 局部同质性与公平性的理论联系： 文章建立了局部同质性和公平性之间的理论联系，展示了节点处理如何随着OOD问题的严重程度而变化。

• 新的GNN公平性基准： 作者引入了三个具有自然敏感属性和广泛局部同质性水平的新基准，以研究OOD问题。

• 半合成数据生成： 提出了一种基于图重连的半合成图生成策略，通过最优传输在局部同质性子群之间调整图的局部同质性分布。

实验结果：

文章通过在真实世界和半合成数据集上的广泛分析，发现两个因素可以促进不公平：(a) OOD距离，(b) 位于同质性图中的异质性节点。在满足这两个条件的情况下，真实世界数据集上的公平性下降了高达24%，半合成数据集上则下降了30%。

实验验证：

作者通过实验验证了理论发现，使用了OOD训练框架来控制训练和测试集之间同质性水平的差异。此外，文章还提出了一种新的半合成图生成策略，通过图重连精确控制局部同质性模式，进一步探索了不同的局部同质性分布。

文章的贡献不仅在于提出了一个新的理论框架和实验方法来研究GNNs的公平性问题，而且还在于它为GNNs的设计提供了新的视角，特别是在处理具有不同局部同质性水平的图数据时。通过引入新的基准和数据生成方法，文章为未来在这一领域的研究提供了宝贵的资源。此外，文章还强调了在设计GNNs时考虑局部结构的重要性，以避免由于图结构的代表性不足而引起的公平性问题。