三个实例迅速掌握经典卡尔曼滤波用法

一、经典卡尔曼滤波器

假设我们系统(线性的)的离散状态空间方程如下,其中，ABCD是状态矩阵，w(k)和v(k)分别代表过程噪声和系统噪声，假设过程噪声和测量噪声的房差分别为Q和R。

在这个状态空间方程基础上，我们可以使用经典卡尔曼滤波器进行状态观测。

1、状态预测

带帽子的x表示估计的意思，右上角再加-表示先验估计状态（纯计算）。直观上理解，就是拿上一刻的滤波结果hat_x(k-1)和输入u(k-1)，直接套公式，算出一个理论的估算结果。

2、误差协方差预测

引入的过程噪声方差Q，直观上可以理解为，对状态预测结果精度的评价。

3、卡尔曼增益计算

卡尔曼滤波的关键所在，计算权重系统，决定观测值对最终结果的影响程度，Kk的值在0到1之间。

4、状态更新

卡尔曼滤波灵魂所在，直观上理解，如果Kk的值为0，则,表示完全相信套公式计算的结果；如果Kk的值为1，且正常情况下，C元素是1，则，完全相信测量的结果；当Kk在0~1之间时，则是测量结果与计算结果的融合。

5、误差协方差更新

更新误差协方差矩阵，进入下一轮循环。

至于这五个公式怎么来的，学有余力的同学可以b站学习下总线博士的视频，至于博主嘛，先用了再说，推导是科学家们的事。

DR_CAN的个人空间-DR_CAN个人主页-哔哩哔哩视频 (bilibili.com)

 二、实例一：测量室内温度

假设室内温度初始温度是25度。但是由于透风、或者晒太阳，温度会有波动，这个波动叫过程噪声，我们假设过程噪声方差Q=0.01；我们拿温度计测量室内温度，温度计也有精度误差，再加上我们眼花可能也会看错，这个误差我们假设在±0.5℃上波动，测量噪声方差R=0.25；这是一个一维系统，状态空间方程如下：

即:A=1,B=0,C=1,D=0,Q=0.01,R=0.25; 下面开始套参环节：

clc;clear;close all;
% 系统参数
Temp=25;          %房间初始温度
dt=0.001;

% 状态空间模型
A=1;
B=0;
C=1;
D=0;

%卡尔曼滤波器初始化
P = 1;             % 估计协方差矩阵初始值
Q = 0.01;          % 过程噪声协方差矩阵
R = 0.25;          % 测量噪声协方差
x_est(1) = 25;    % 状态估计初始值
I=eye(length(x_est));

% 模拟数据
t = 0:dt:10;
x_true = zeros(1, length(t)); %存放真实值
z = zeros(size(t));           %存放测量值

% 初始条件
x_true(1) = Temp;
z(1) = C*x_true(:,1) + sqrt(R)*randn;

% 模拟系统和测量
for i = 2:length(t)
    % 真实系统更新，计算机模拟系统
    x_true(i) = A*x_true(i-1) + sqrt(Q)*randn;
    % 生成测量数据
    z(i) = C*x_true(i) + sqrt(R)*randn;          
    % 调用卡尔曼滤波更新
    [x_est(i), P] = kalman_filter(x_est(i-1), 0, P, z(i), A, C, Q, R,B); 
end
figure
hold on;grid on;box on;
plot(t,z); % 真实位移
plot(t,x_true); % 真实位移
plot(t,x_est);  % 滤波后的位移
xlabel('时间 s');
ylabel('位移  m');
title('卡尔曼滤波 位移x')
legend('x mea','x true','x est');

function [x_est, P] = kalman_filter(x_est,u, P, z, A, C, Q, R, B)
    % 预测
    x_pre = A*x_est + B*u;
    P_pre = A*P*A' + Q;

    % 更新
    K = P_pre*C' / (C*P_pre*C' + R);
    x_est = x_pre + K * (z - C*x_pre);
    P = (eye(length(x_est)) - K*C) * P_pre;
end

运行结果如下：

 估算的结果与真实结果非常接近。相比测量结果，少了很多噪声。至于温度为什么上升了，跟matlab生成随机数randn函数有关系。

显然，这是在MATLAB脚本里仿真，总感觉跟真实系统相比差点意思？我们把卡尔曼滤波这五个公式搬进simulink模型，并将房间温度模拟当做一个实体plant，如下图所示（也可以用simulink自带的kf模块)。

 运行结果如下：

 三、实例二：自由落体物体实例

假设一个小球从1000m的高空自由落体，忽略空气阻力，只受重力影响。地面有个雷达站，实时观测小球的位置，下面我们建立状态空间方程

 设物体的位移s,物体的速度为v

是假设Q1=Q2=0.01;R=1; 接下来跟上一个实例类似，进入套参数环节。

clc;clear;close all; 
% 系统参数
dt=0.001;
InitialHigh=1000;
u=-10;
% 状态空间模型
A=[1 dt;0 1];
B=[0.5*dt*dt;dt];
C=[1 0];
D=0;

%卡尔曼滤波器初始化
P = [1 0;0 1];             % 估计协方差矩阵初始值
Q = [0.01 0;0 0.01];       % 过程噪声协方差矩阵
R = 1;                     % 测量噪声协方差
x_est(:,1) = [InitialHigh;0];% 状态估计初始值
I=[1 0;0 1];

% 模拟数据
t = 0:dt:10;
x_true = zeros(2, length(t)); %存放真实值
z = zeros(size(t));           %存放测量值

% 初始条件
x_true(:,1) = [InitialHigh;0];
z(1) = C*x_true(:,1) + sqrt(R)*randn;

% 模拟系统和测量
for i = 2:length(t)
    % 真实系统更新，计算机模拟系统
    x_true(:,i) = A*x_true(:,i-1) + B*u+sqrt(Q)*randn(2,1);
    % 生成测量数据
    z(i) = C*x_true(:,i) + sqrt(R)*randn;          
    % 调用卡尔曼滤波更新
    [x_est(:,i), P] = kalman_filter(x_est(:,i-1), u, P, z(i), A, C, Q, R,B); 
end
figure
hold on;grid on;box on;
plot(t,z); % 真实位移
plot(t,x_true(1,:)); % 真实位移
plot(t,x_est(1,:));  % 滤波后的位移
xlabel('时间 s');
ylabel('高度  m');
title('卡尔曼滤波 高度h')
legend('h mea','h true','h est');

figure
hold on;grid on;box on;
plot(t,x_true(2,:)); % 真实速度
plot(t,x_est(2,:));  % 滤波后的位移
xlabel('时间 s');
ylabel('速度  m/s');
title('卡尔曼滤波 速度v');
legend('v true','v est');

sim KalModel2.slx;

function [x_est, P] = kalman_filter(x_est,u, P, z, A, C, Q, R, B)
    % 预测
    x_pre = A*x_est + B*u;
    P_pre = A*P*A' + Q;

    % 更新
    K = P_pre*C' / (C*P_pre*C' + R);
    x_est = x_pre + K * (z - C*x_pre);
    P = (eye(length(x_est)) - K*C) * P_pre;
end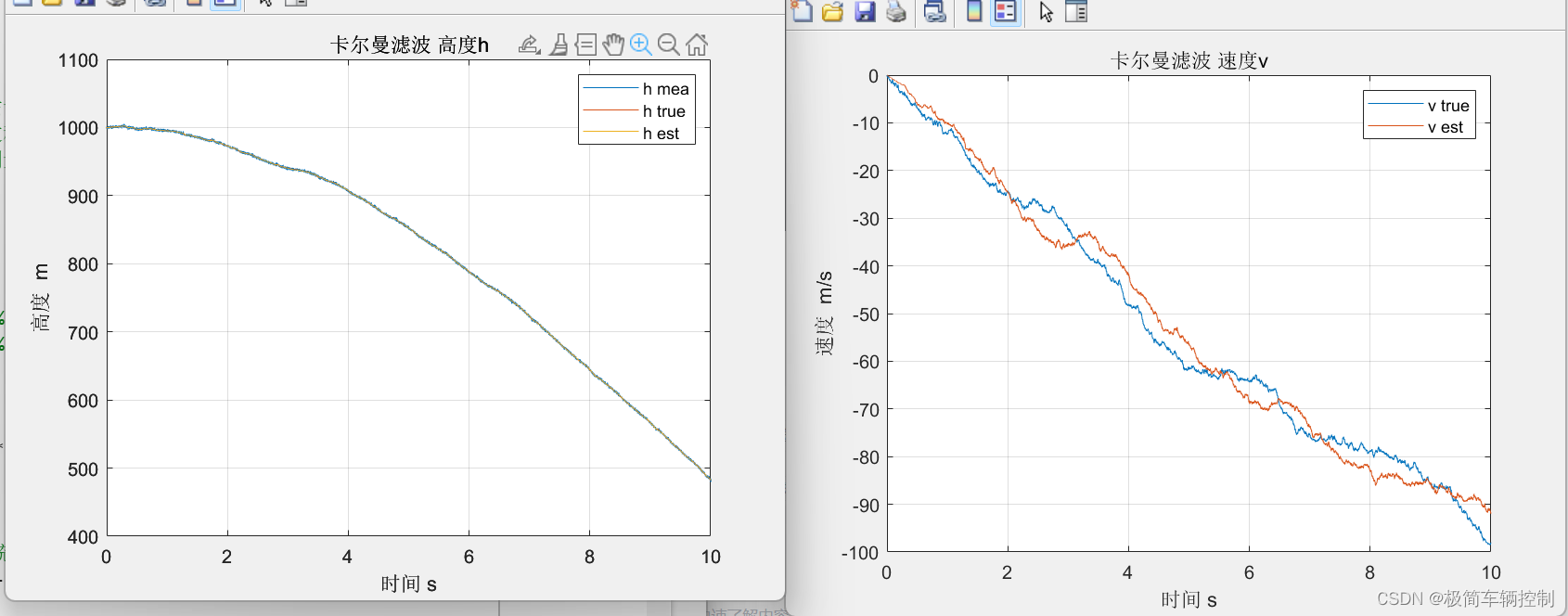

在simulink模型中

从这个实例中，可以体会到前面文章提到的观测器味道了。测量一个状态量，通过这个状态量和输入，估算另一个状态量。

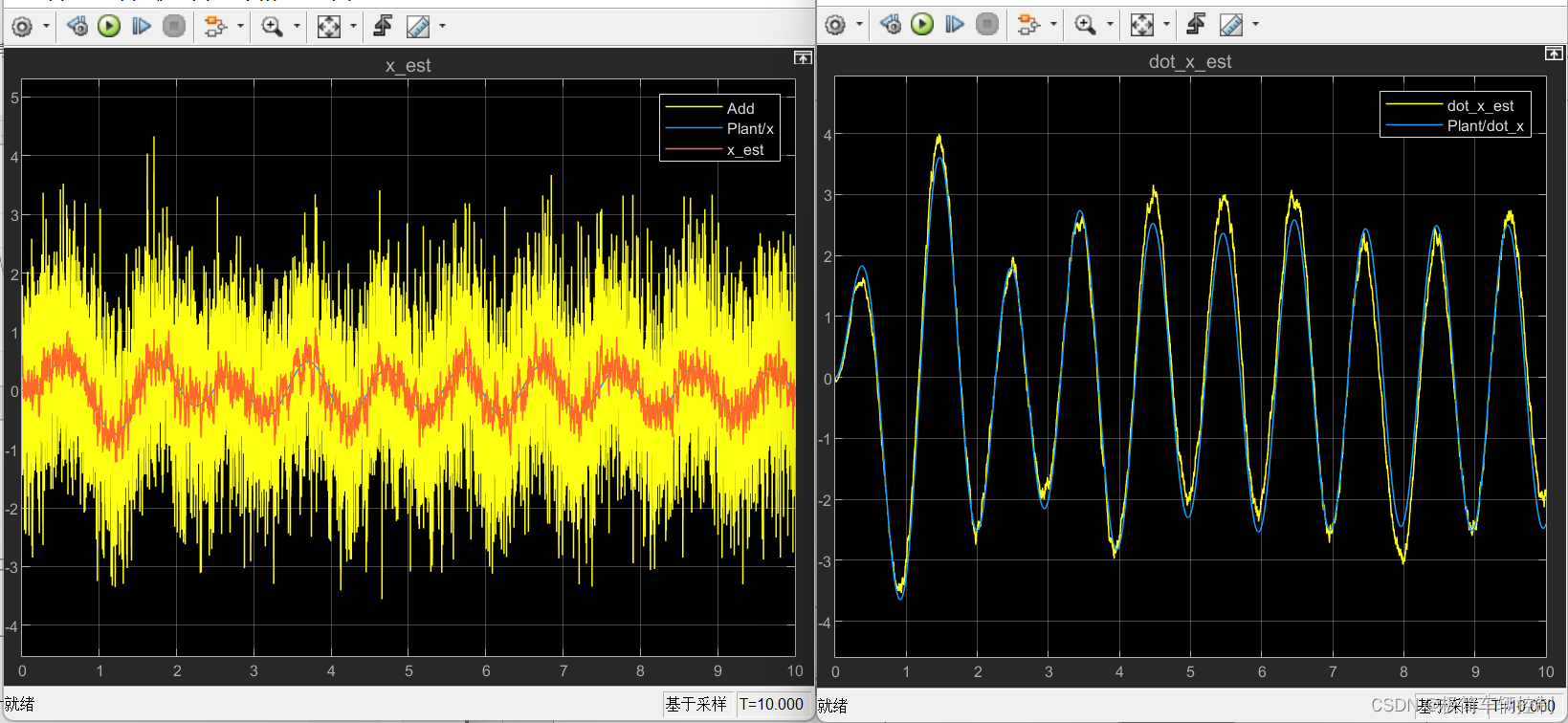
四、实例三：弹簧-阻尼系统

如下图所示的弹簧阻尼系统，通过牛顿第二定律，建立微分方程，得到连续状态空间方程。

 在这个系统中，测量位移x，估计速度v；假设过程噪声Q = 0.01 * eye(2)，测量噪声R=1；假设质量M=10； k=150;c=10。与前两个例子不同，在套用卡尔曼滤波器之前，需要将连续系统先离散化。输入力F可以设定输入正弦信号。

 在simulink中，同样套用前两个例子的模型，运行得到结果。

五、关于脚本和模型

关键步骤脚本和模型框架已经贴出，如果需要源模型和代码，还是在某宝店<极简车辆控制>中。