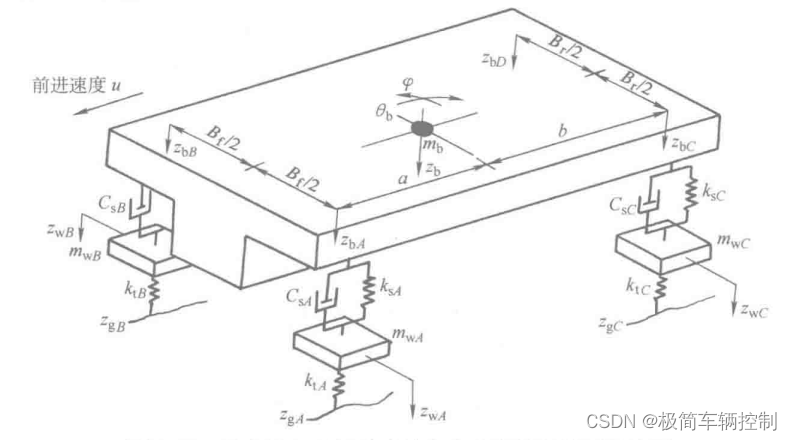
如上图所示的独立悬架7自由度整车模型,假定车身是一个刚体,车辆在水平面上做匀速直线运动,车身具有上下跳动、俯仰和侧倾三个自由度,四个车轮各自都有一个上下跳动的自由度,加起来总共有7个自由度,所以称为简化的7自由度悬架振动模型。
图中参数说明:
Bf,Br:前轴轮距,后轴轮距
KtA,KtB,KtC,KtD :前后左右四个轮胎刚度
ZgA,ZgB,ZgC,ZgD:前后左右四个轮胎处路面激励
ZwA,ZwB,ZwC,ZwD:前后左右四个车轮质心位移
CsA,CsB,CsC,CsD: 前后左右减振器阻尼系数
KsA,KsB,KsC,KsD:前后左右弹簧刚度
ZbA,ZbB,ZbC,ZbD:前后左右四个角落车身位移
θb:车身俯仰角度:车身侧倾角度
zb:车身质心上下运动位移
a,b:质心到前轴和后轴距离
在CDC控制中,建立7自由度悬架模型主要目的还是:
1、分析粗糙路上质心振动加速度优化情况;
2、整车行驶车身姿态运动控制(俯仰、侧倾);
3、过减速带工况;
假设车身是刚体,质心运动Zb,θb和数值都较小,从几何关系,可以得到车身四个角落簧上位移如下:
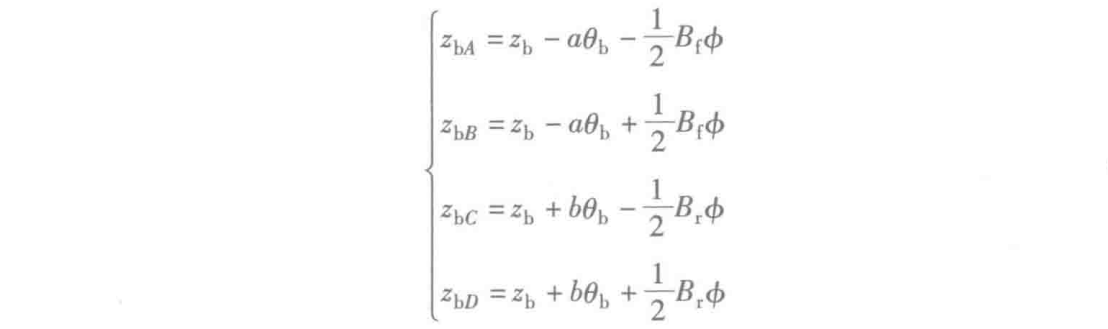
车身质心处垂向运动方程为:
车身俯仰运动方程为: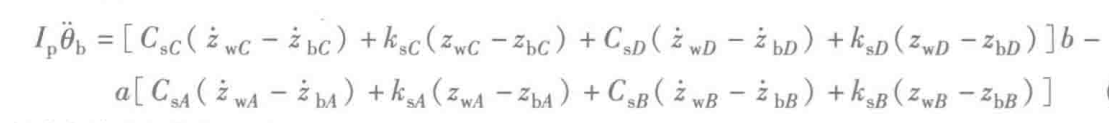
车身侧倾运动方程为:
四个非簧载质量(簧下质量)运动方程:
从以上五组方程,便可以搭建出悬架仿真7自由度模型,下面打开simulink,开始搭模型:
1、有二阶微分的,二话不说,先摆上两个积分器,并标注好名称,然后根据解析式,一个一个把它们接起来: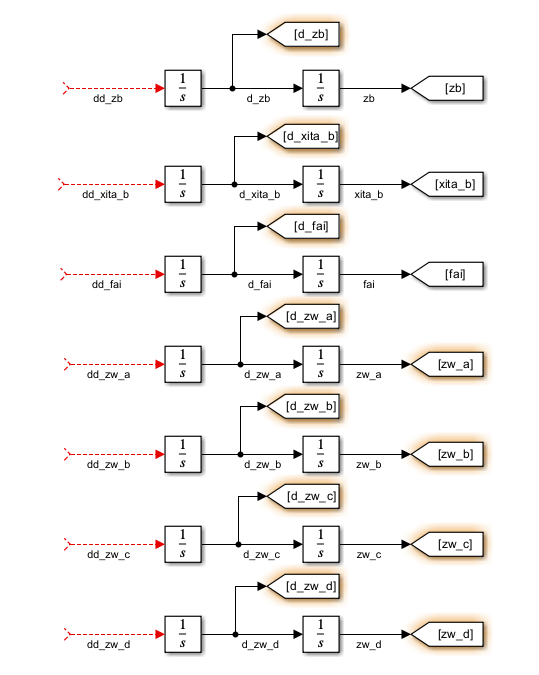
2、搭第一组方程,四个角落的位移,输出都已经有了。
考虑到簧上位移的微分,别处也有用,顺便搭出来。
3、 接着,可以搭zb两点的求解,就可以跟第一步的zb两点连起来了。
4、搭建第三组,俯仰运动方程.

5、搭第四组方程,侧倾运动,第4步和第5步很多是可以从第三步复制过来的。
6、搭最后一组方程.
7、按照先后顺序,整理下这几个模块,取缔掉一些goto,信号合并为总线输出的形式,稍作整理。输入为随机路面,随机路面的生成前几个文章有讲过。

8、设置车辆参数:
mb=1380; %车身质量kg
Ip=2440; %俯仰转动惯量 kg.m2
Ir=380; %侧倾转动惯量 kg.m2
Bf=1.48; %前轴轮距
Br=1.48;%后轴轮距
KtA=192; %KN/m 左前轮胎刚度
KtB=192; %KN/m 右前轮胎刚度
KtC=192; %KN/m 左后轮胎刚度
KtD=192; %KN/m 右后轮胎刚度
KsA=17; %KN/m 左前弹簧刚度
KsB=17; %KN/m 右前弹簧刚度
KsC=17; %KN/m 左后弹簧刚度
KsD=17; %KN/m 右后弹簧刚度
CsA=1.5; %KN.s/m 左前减振器阻尼
CsB=1.5; %KN.s/m 右前减振器阻尼
CsC=1.5; %KN.s/m 左后减振器阻尼
CsD=1.5; %KN.s/m 右后减振器阻尼
a=1.25;% m 质心到前轴距离
b=1.51;%m质心到后轴距离
m_wa=40.5;%左前簧下质量
m_wb=40.5;%右前簧下质量
m_wc=45.4;%左后簧下质量
m_wd=45.4;%右后簧下质量运行仿真,查看结果。
质心加速度

























 1991
1991

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










