计算理论Computing Theory_Chapter01

Set

 

elements/members
singleton: (one element)
empty set
proper set
union
intersection
difference:

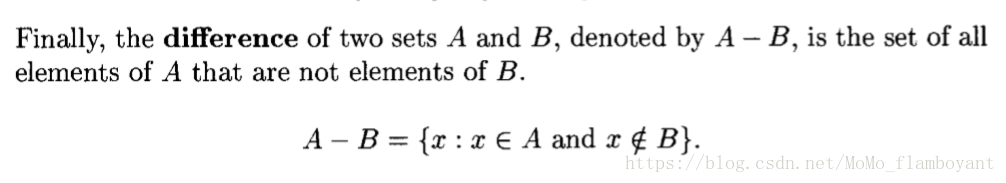
Idempotency, Commutativity, Associativity, Distributivity, Absorption, DeMorgan's laws:

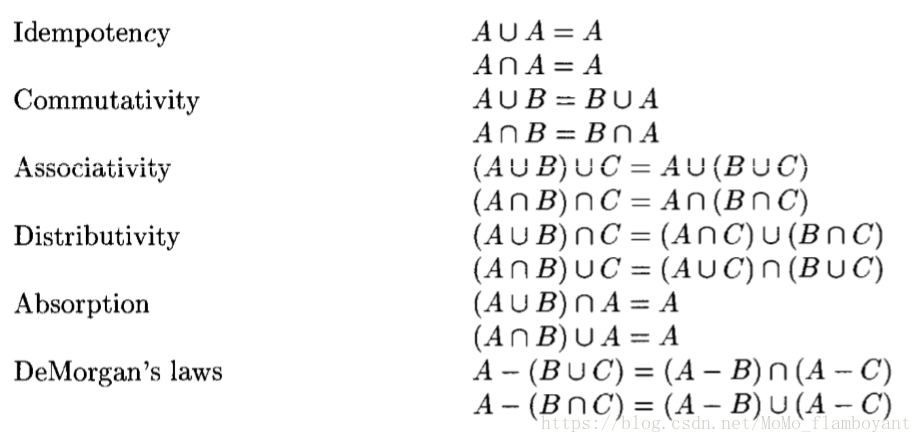
disjoint:

 

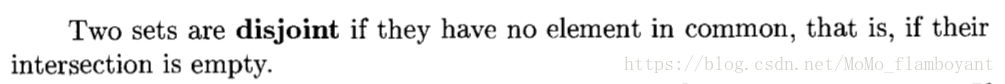
Why we need sets of sets?

to represent power sets -- all the subsets of a set, as well as partition.

 

Intersections and Unions of more than two sets:

If S is any collection of sets, we write  for the set whose elements are the elements of all the sets in S.

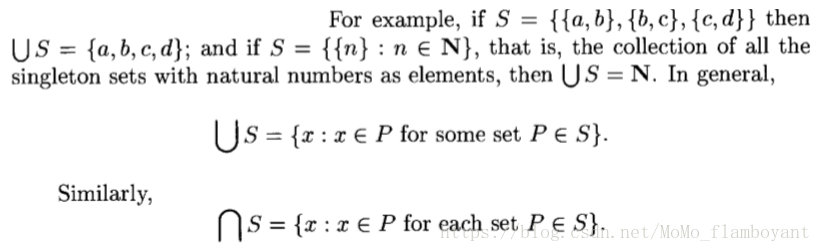
eg. S = { {a,b}, {b,c}, {c,b,d} } -->  = {a,b,c,d}, = {b}.

power set: The collection of all subsets of a set A is itself a set, called the power set of A and denoted 

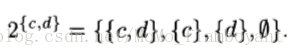
parition:

 

 

 

 

Relations

A relation is itself a set.

The objects that belong to the relation are, in essence, the combinations of individuals for which that relation holds in the intuitive sense. (属于关系的对象在本质上是直观上使得关系成立的个体的组合)

So the less-than relation is the set of all pairs of numbers such that the first number is less than the second.

 

basis

ordered pair (to distinguish the two parts or objects, namely components of the pair):

(a,b)   a==b is valid

Cartesian product    is also a set:

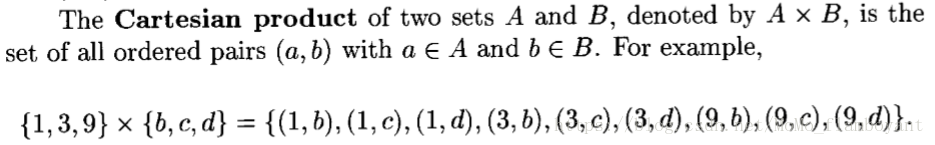
binary relation    a subset of Cartesian product:

The less-than relation is the subset of ​.

 

generalizations

ordered n-tuple   <---   ordered 2-tuple == ordered pair

(b1, b2, ..., bm) == (a1, a2, ..., an)  if and only if  m == n && bi == ai for i = 1, 2, ..., n.

n-fold Cartesian product, set of ordered n-tuples   <---   (2-fold) Cartesian product, set of ordered pairs

n-ary relation, subset of n-fold Cartesian product   <---   (binary) relation, subset of 2-fold Cartesian product

 

 

 

 

 

Functions

function:

A function is an association of each object of one kind with a unique object of another kind.
A function from a set A to a set B is a binary relation R on A and B with the following property:

 

f is function from A to B 

 

basis

domain: A

image:

a is an element that belongs to A,   (a,b) belongs to f,    b == f(a) is an image of a under f;

A' is a subset of A,   (a',b) belongs to f, where a' belongs to A',  b == f[A'] is an image of A' under f;

range:  the range of f is the image of its domain A.<