TransH 算法详解
算法背景
transE算法存在的问题
在我的上一篇博客中,提到了TransE算法。其在知识表示的引用中因为其简单,高效的特性而广受欢迎。但是其也存在一定的缺陷。例如在处理自反关系,以及一对多、多对一、多对多关系时存在一些不足。
通过上一篇博客容易知道,TransE算法的核心思想是对于一个三元组 ( h , r , t ) ∈ Δ (h, r, t) \in \Delta (h,r,t)∈Δ( Δ \Delta Δ 表示正确的三元组集合 Δ ′ \Delta ' Δ′表示不正确的三元组集合,所以 ( h , r , t ) ∈ Δ (h, r, t) \in \Delta (h,r,t)∈Δ表示这个三元组 ( h , r , t ) (h, r, t) (h,r,t)是正确的),那么应该有 h + r = d h+r = d h+r=d。于是可以从TransE模型中得到两个结论:
- 如果 ( h , r , t ) ∈ Δ (h,r,t) \in \Delta (h,r,t)∈Δ 并且 ( t , r , h ) ∈ Δ (t,r,h) \in \Delta (t,r,h)∈Δ ,即 关系r 是一个自反的映射,那么可以知道 r = 0 r = 0 r=0并且 h = t h = t h=t
- 如果 ∀ i ∈ { 0 , 1 , 2 , . . . , m } , ( h i , r , t ) ∈ Δ \forall i \in \{0,1,2,...,m\}, (h_i,r,t) \in \Delta ∀i∈{0,1,2,...,m},(hi,r,t)∈Δ, 也就是说 r 是一个 m - 1的映射,那么 h 0 = . . . . = h m h_0 = .... = h_m h0=....=hm。 相似的,如果 ∀ i ∈ { 0 , 1 , 2 , . . . , m } , ( h , r , t i ) ∈ Δ \forall i \in \{0,1,2,...,m\}, (h,r,t_i) \in \Delta ∀i∈{0,1,2,...,m},(h,r,ti)∈Δ, 也就是说 r 是一个 m - 1的映射,那么 t 0 = . . . . = t m t_0 = .... = t_m t0=....=tm。
从上述结果可以发现,transE算法在处理自反关系,以及多对一、一对多、多对多关系中,会使得一些不同的实体具有相同或者相似的向量。其根本原因在于,出现在多个关系中的同一个实体的表示是相同的。
解决方法
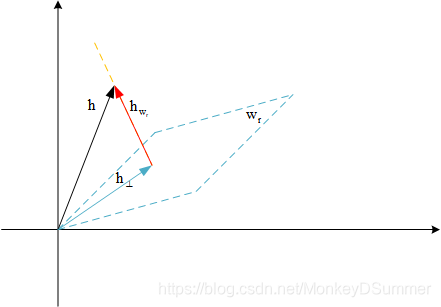
为了解决TransE在面对自反关系,以及多对一、一对多、多对多关系的不足。2014年Wang Z, Zhang J, Feng J, et al.提出了transH模型,其核心思想是对每一个关系定义一个超平面 W r W_r Wr,和一个关系向量 d r d_r dr。 h ⊥ , t ⊥ h_{\perp },t_{\perp } h⊥,t⊥是 h , t h,t h,t在 W r W_r Wr上的投影,这里要求正确的三元组需要满足 h r + d r = t r h_r + d_r = t_r hr+dr=tr。这样能够使得同一个实体在不同关系中的意义不同,同时不同实体,在同一关系中的意义,也可以相同。
算法描述
几何含义

如上图所示, 对于正确的三元组 ( h , r , t ) ∈ Δ (h, r, t) \in \Delta (h,r,t)∈Δ 来说,其所需要满足的关系如图所示。那么对于一个实体 h " h" h" 如果满足 ( h " , r , t ) ∈ Δ (h", r, t) \in \Delta (h",r,t)∈Δ,在transE中是需要 h " = h h" = h h"=h,而在transH算法中则将约束放宽到 h , h " h,h" h,h"在 W r W_r Wr上的投影相同就行了,也就能将 h " , h h",h h",h区分开来,从而具有不同的表示。
目标函数
于是我们定义在transE中的
d
(
h
+
r
,
t
)
d(h+r,t)
d(h+r,t)为:
d
(
h
+
r
,
t
)
=
f
r
(
h
,
t
)
=
∣
∣
h
⊥
+
d
r
−
t
⊥
∣
∣
2
2
d(h+r,t) = f_r(h,t) = || h_{\perp} + d_r - t_{\perp}||_2 ^2
d(h+r,t)=fr(h,t)=∣∣h⊥+dr−t⊥∣∣22
对于平面
W
r
W_r
Wr我们可以用法向量来表示,我们不妨假设
w
r
w_r
wr为平面
W
r
W_r
Wr的法向量,并加约束条件
∣
∣
w
r
∣
∣
2
2
=
1
||w_r||_2 ^2 = 1
∣∣wr∣∣22=1, 所以我们知道
h
h
h在
w
r
w_r
wr上的投影为
h
w
r
=
w
T
h
w
h_{w_r} = w^T h w
hwr=wThw,这是因为
w
T
h
=
∣
w
∣
∣
h
∣
c
o
s
θ
w^Th=|w||h|cos\theta
wTh=∣w∣∣h∣cosθ表示
h
h
h在
w
w
w方向上投影的长度(带正负号),乘以
w
w
w即
h
h
h在
w
w
w上的投影,所以可以知道:
h
⊥
=
h
−
h
w
r
=
h
−
w
T
h
w
h_{\perp} = h - h_{w_r} = h - w^T h w
h⊥=h−hwr=h−wThw
如下图所示
相似的可以知道
t ⊥ = t − t w r = t − w r T t w r t_{\perp} = t - t_{w_r} = t - w_r ^T t w_r t⊥=t−twr=t−wrTtwr
所以
f r ( h , t ) = ∣ ∣ h − w r T h w r + d r − t + w r T t w r ∣ ∣ 2 2 f_r(h,t) = || h - w_r^T h w_r + d_r - t + w_r^T t w_r||_2 ^2 fr(h,t)=∣∣h−wrThwr+dr−t+wrTtwr∣∣22
所以得到目标函数
min ∑ ( h , r , t ) ∈ S ∑ ( h ′ , r , t ′ ) ∈ S ′ [ γ + f r ( h , t ) − f r ( h ′ , t ′ ) ] + \min {\sum _ {(h,r,t) \in S} \sum _{(h', r, t') \in S'} [\gamma + f_r(h , t) - f_r(h',t')]_+} min(h,r,t)∈S∑(h′,r,t′)∈S′∑[γ+fr(h,t)−fr(h′,t′)]+
梯度
定义:
l
=
[
γ
+
f
r
(
h
,
t
)
−
f
r
(
h
′
,
t
′
)
]
+
=
[
γ
+
(
h
−
w
r
T
h
w
r
+
d
r
−
t
+
w
r
T
t
w
r
)
2
−
(
h
′
−
w
r
T
h
′
w
r
+
d
r
−
t
′
+
w
r
T
t
′
w
r
)
2
]
+
l = [\gamma + f_r(h , t) - f_r(h',t')]_+ = [\gamma + (h - w_r^T h w_r + d_r - t + w_r^T t w_r) ^ 2 - (h' - w_r^T h' w_r + d_r - t' + w_r^T t' w_r)^2]_+
l=[γ+fr(h,t)−fr(h′,t′)]+=[γ+(h−wrThwr+dr−t+wrTtwr)2−(h′−wrTh′wr+dr−t′+wrTt′wr)2]+
于是有:
∂
l
∂
h
=
{
2
(
h
−
w
r
T
h
w
r
+
d
r
−
t
+
w
r
T
t
w
r
)
⋅
(
i
^
−
(
w
i
2
)
⃗
)
,
if
l
>
0
;
0
,
if
l
<
=
0
\frac{\partial l}{\partial h} = \begin{cases} 2(h - w_r^T h w_r + d_r - t + w_r^T t w_r)\cdot(\hat i - \vec{(w_i ^2)} ), & \text{if } l > 0;\\ 0, &\text{if } l <= 0 \end{cases}
∂h∂l={2(h−wrThwr+dr−t+wrTtwr)⋅(i^−(wi2)),0,if l>0;if l<=0
∂ l ∂ t = { 2 ( h − w r T h w r + d r − t + w r T t w r ) ⋅ ( i ^ − ( w i 2 ) ⃗ ) , if l > 0 ; 0 , if l < = 0 \frac{\partial l}{\partial t} = \begin{cases} 2(h - w_r^T h w_r + d_r - t + w_r^T t w_r)\cdot(\hat i - \vec{(w_i ^2)} ), & \text{if } l > 0;\\ 0, &\text{if } l <= 0 \end{cases} ∂t∂l={2(h−wrThwr+dr−t+wrTtwr)⋅(i^−(wi2)),0,if l>0;if l<=0
∂ l ∂ h ′ = { 2 ( h ′ − w r T h ′ w r + d r − t ′ + w r T t ′ w r ) ⋅ ( i ^ − ( w i 2 ) ⃗ ) , if l > 0 ; 0 , if l < = 0 \frac{\partial l}{\partial h'} = \begin{cases} 2(h' - w_r^T h' w_r + d_r - t' + w_r^T t' w_r)\cdot(\hat i - \vec{(w_i ^2)} ), & \text{if } l > 0;\\ 0, &\text{if } l <= 0 \end{cases} ∂h′∂l={2(h′−wrTh′wr+dr−t′+wrTt′wr)⋅(i^−(wi2)),0,if l>0;if l<=0
∂ l ∂ t ′ = { 2 ( h ′ − w r T h ′ w r + d r − t ′ + w r T t ′ w r ) ⋅ ( i ^ − ( w i 2 ) ⃗ ) , if l > 0 ; 0 , if l < = 0 \frac{\partial l}{\partial t'} = \begin{cases} 2(h' - w_r^T h' w_r + d_r - t' + w_r^T t' w_r)\cdot(\hat i - \vec{(w_i ^2)} ), & \text{if } l > 0;\\ 0, &\text{if } l <= 0 \end{cases} ∂t′∂l={2(h′−wrTh′wr+dr−t′+wrTt′wr)⋅(i^−(wi2)),0,if l>0;if l<=0
∂ l ∂ w r = { 2 ( h − w r T h w r + d r − t + w r T t w r ) ⋅ ( w T t − w T h ) ( t − h ) − 2 ( h ′ − w r T h ′ w r + d r − t ′ + w r T t ′ w r ) ⋅ ( w T t ′ − w T h ′ ) ( t ′ − h ′ ) , if l > 0 ; 0 , if l < = 0 \frac{\partial l}{\partial w_r} = \begin{cases} 2(h - w_r^T h w_r + d_r - t + w_r^T t w_r)\cdot(w^Tt -w^Th)(t - h) - \\ 2(h' - w_r^T h' w_r + d_r - t' + w_r^T t' w_r)\cdot(w^Tt' -w^Th')(t' - h'), & \text{if } l > 0;\\ 0, &\text{if } l <= 0 \end{cases} ∂wr∂l=⎩⎪⎨⎪⎧2(h−wrThwr+dr−t+wrTtwr)⋅(wTt−wTh)(t−h)−2(h′−wrTh′wr+dr−t′+wrTt′wr)⋅(wTt′−wTh′)(t′−h′),0,if l>0;if l<=0
其中
i
^
\hat i
i^ 是单位向量;
(
w
i
2
)
⃗
=
(
w
1
2
,
w
2
2
,
.
.
.
)
\vec{(w_i ^2) }= (w_1^2, w_2^2,...)
(wi2)=(w12,w22,...)也是一个向量。
用到的知识有 链式求导法则和向量的求导法则。 自己算的不确定算的对不对 希望大佬们帮忙指正,谢谢!
























 1030
1030

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








