机器学习优化算法：牛顿法以及海森矩阵

参考：海森矩阵和牛顿法

          人工智能-损失函数-优化算法：牛顿法的背后原理【二阶泰勒展开】

          牛顿法与Hessian矩阵

给出一个总结：

牛顿法法主要是为了解决非线性优化问题，其收敛速度比梯度下降速度更快。其需要解决的问题可以描述为：对于目标函数f(x)，在无约束条件的情况下求它的最小值。

牛顿法的主要思想是：在现有的极小值估计值的附近对做二阶泰勒展开，进而找到极小点的下一个估计值，反复迭代直到函数的一阶导数小于某个接近0的阀值。

1. 求解方程的根

我们先从一个最简单的情况来分析。

当方程没有求根公式，或者求根公式很复杂而导致求解困难时，怎么办呢？此时牛顿法就起作用了。

这里假设我们要求的根。步骤如下：

• 首先，选择一个接近函数的 ，计算相应的 和切线斜率。
• 然后计算穿过点并且斜率为的直线和 轴的交点的坐标，也就是求如下方程的解（公式1）：

  

我们这里给出公式1一个非常可观的推导：

假设新方程为，将斜率带入有：。

由于过点，进一步带入可以得到：

因此对于新的方程有：

令新方程等于0，即为：

• 我们将新求得的点的 坐标命名为。可以看到，会比更接近方程的解。因此我们现在可以利用开始下一轮迭代。我们对公式1进行变换，得到公式2：

                                                         

通过公式2不断地迭代，就可以越来越接近  的根。整个的过程可以由下图表示：

在上面，我们利用求解直线方程的方式，给出了公式1最为直接的推导方法。这里我们给出从泰勒展开推导的过程：

根据我们在处进行泰勒展开，如下：

我们只保留一阶以及一阶之前的部分：

令，进一步通过移项整理可得下式，与公式2一致。

 

因此可以看到，迭代公式就是是泰勒一阶展开。

这里必须要说明的是：

2. 最优化问题——二阶牛顿法

在1.中我们求的是方程等于0的解。在实际的机器学习优化算法中，我们的目标是最小化目标函数的值：

                                                                  

根据数学知识，最小的值的一阶导数往往等于0，因此可以转化为求。

这里参考二阶泰勒展开公式：

然后对求导，得：

之后令有：

进一步移项有：

对于高维函数，牛顿法通用公式可以写成：

3. 牛顿法 与 Hessian矩阵的关系

以上牛顿法的推导是针对单变量问题的，但是对于机器学习，往往是多变量的情况。这里假设有k个参数，即表示第k个参数。那么对于需要优化的目标，对其进行二阶展开有：

其中表示在处的一阶导数，也就是梯度。并且，因为是多变量的情况，因此写成了矩阵相乘的形式。

跟前面的推导一样，我们对求一阶导数，有：

 那么极值点的求解就是令上式子为0，有：

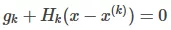
于是就有：

上面的式子中，H就是Hessian矩阵，它对应的是二阶偏导数。g为雅可比矩阵，对应的是一阶偏导数。

Hessian矩阵：

 

雅可比矩阵：

: