期望和方差

已于 2024-09-09 11:07:48 修改
阅读量7.4k 收藏 14
点赞数 3
分类专栏： 概率论 数学 文章标签： 概率论 数学
于 2022-08-29 11:03:04 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/Mr_health/article/details/126580358
版权

主要介绍推公式可能会经常用的期望和方差的相关公式

期望

1. 基本公式

连续型随机变量x的期望计算公式：

若随机变量Y符合函数Y = g(x),且绝对收敛，那么随机变量Y的期望计算公式为：

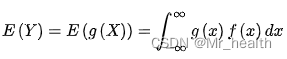（公式1）

2. 性质

主要记住以下几种性质即可

方差

方差在统计描述和概率分布中各有不同的定义，并有不同的公式。我们首先来看一下统计视角的

1. 统计视角

2. 概率视角-基本公式

在概率的视角，前面我们定义了E(X)为期望，那么方差的定义为：随机变量值X与其期望值E(X)之差的平方的期望值，公式如下：

当随机变量的参数X是离散的时候，公式可以写为：

对于连续型随机变量X，若其定义域为(a,b)，其概率密度为f(x)，期望为μ，那么其方差的计算公式为：

这个公式其实可以通过我们前面公式（1）推导出来，相当于g(x) = x - E(X) = x - \mu

 3. 性质

另外补充一下当随机变量X、Y独立时，XY的方差D(XY)计算公式：

这里面有一个非常重要点的点在于E(X)和E(Y)的均值为0

期望和方差的性质
一个搬运知识的笨小孩
02-15 5091
1.期望和方差的性质 1.1 性质一 当只有一个随机变量XXX，利用期望的定义来计算E[a1g1(X)+a2g2(X)]E[a_1g_1(X)+a_2g_2(X)]E[a1​g1​(X)+a2​g2​(X)] 期望的定义 当有两个不同的随机变量X=X1+X2X=X_1+X_2X=X1​+X2​ 1.2 性质二 如果gi(Xi)=cg_i(X_i)=cgi​(Xi​)=c，那么E[gi(Xi)]=cE[g_i(X_i)]=cE[gi​(Xi​)]=c 1.3 性质三 先给出方差的定义 1.4
常见分布的期望和方差推导
一个搬运知识的笨小孩
06-01 979
手写推导常见分布的期望和方差
理解 期望(均值/估计值)和方差
songhuangong123的博客
06-27 1万+
开始会给出公式，后面结合正态分布的的期望和方差，来更具体的理解他们。首先，期望全名“数学期望”，又名均值或估计值，注意和平均值不是一个概念。这个后续再说。说到期望，就得先说分布列。X 表示不同种类的事件对应的数值，P表示每钟事件发现的概率 。什么叫做事件对应的数值，这其实是我们自己下的一个定义，比如抛正面得1分。再比如： 这里得到得分布列应该是： 那么有了分布列，就可以求期望了，或者说求均值/估计值。这里用EX表示期望： 哪有了分布列，求期望和非常简单的。(如上图：相乘再相加)。这里也看出了它与平均值的不同
【数学】期望、方差、协方差、协方差矩阵
zhuhua造轮子的博客
05-21 1万+
期望、方差、协方差、协方差矩阵 1 期望（数学期望、均值） 在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小。 需要注意的是，期望值并不一定等同于常识中的“期望”——“期望值”也许与每一个结果都不相等。期望值是该变量输出值的平均数。期望值并不一定包含于变量的输出值集合里。 大数定律...
期望、方差和协方差
最新发布
Shockang的博客
03-06 1095
本文深入解析了期望、方差与协方差核心概念，结合Python代码实现与金融投资组合等实践案例，揭示统计原理在机器学习模型优化、特征工程和异常检测中的关键作用，助您掌握数学理论与工程应用的深度结合。
期望、方差
Anne033的博客
10-03 6万+
一、期望和方差的定义 随机变量(Random Variable) X 是一个映射，把随机试验的结果与实数建立起了一一对应的关系。而期望与方差是随机变量的两个重要的数字特征。 1. 期望(Expectation, or expected value) 期望是度量一个随机变量取值的集中位置或平均水平的最基本的数字特征； 2. 方差(Variance) 方差是表示随机变量取值的分散性的一个数字特征。 方差越大，说明随机变量的取值分布越不均匀，变化性越强；方差越小，说明随机变量的取值越趋近于均值，即期望值。 （1
期望、方差计算
rosefun96的博客
06-18 2万+
1. 期望 定义 设P(x)P(x)P(x)是一个离散概率分布函数，自变量的取值范围为{x1,x2,⋯ ,xn}\{x_1, x_2, \cdots, x_n\}{x1​,x2​,⋯,xn​}。其期望被定义为： E(x)=∑k=1nxkP(xk)E(x)=\sum_{k=1}^n{x_kP(x_k)}E(x)=k=1∑n​xk​P(xk​) 设p(x)p(x)p(x)是...
概率论基础 —— 8.数学期望、方差、协方差
热门推荐
老程的技术笔记
07-24 6万+
我们在学习了离散型和连续型随机概率事件，以及它们的分布函数和密度概率函数之后。接下来我们要学习对概率事件进行评判的技术——期望、方差、协方差。 这些概念有什么用呢，举例来说，对于一次期末考试，如何评估同一个年级的不同班级的学生的学习状况差异，如何找出年级最优班级和最差班级呢，以及在两个班级整体状况都相差不大时，如何比较一个班级学生成绩情况比另一个班级更好呢？ 如果还记得我们前面提到过的概率分布函数，那么就可以知道这一类样本的比较，其实属于对样本的分布规律的分析。 文章目录期望 (Expectation).
5 matlab常见分布的期望和方差.zip
12-18
在MATLAB中，理解和计算各种概率分布的期望与方差是数据分析、建模以及统计建模过程中的关键步骤。期望代表了随机变量的平均值，而方差则衡量了数据的离散程度。本资料包“5 matlab常见分布的期望和方差.zip”可能...
证明 正态分布 的期望和方差
分享各种学习心得和遇到的问题
06-17 8543
正态分布（Normal Distribution）是连续型概率分布中最重要和最常见的一种。假设随机变量 ( X ) 服从均值为 ( \mu )、方差为 ( \sigma^2 ) 的正态分布，记作。这些结果表明，正态分布的均值是 ( \mu )，方差是 ( \sigma^2 )，反映了数据的集中趋势和离散程度。方差（Variance）表示随机变量与其期望值之间的离散程度。第二个积分为零，因为 ( z ) 是奇函数，而 ( e。2}{2}} ) 是偶函数：（奇*偶=奇函数）
证明 指数分布 的期望和方差
分享各种学习心得和遇到的问题
06-17 6565
指数分布（Exponential Distribution）是一种常见的连续型概率分布，通常用于描述事件之间的时间间隔。假设随机变量 ( X ) 服从参数为 ( \lambda ) 的指数分布，记作。这些结果表明，在进行一系列独立的指数分布事件中，事件之间时间间隔的平均值是 ( \frac{1}{\lambda} )，而离散程度由 ( \frac{1}{\lambda^2} ) 决定。为了计算这个积分，我们再次使用分部积分法。为了计算这个积分，我们使用分部积分法。
期望，方差
qqqgg的专栏
04-06 467
import numpy as np arr =np.array([1,2,3,4,5,6]) #求均值 arr_mean = np.mean(arr) #求方差 arr_var = np.var(arr) #求标准差 arr_std = np.std(arr,ddof=1) print("平均值为：%f" % arr_mean) print("方差为：%f" % arr_var) prin...
常用统计数学公式学习（1）方差与期望值
handsomeman20的专栏
02-15 1万+
怎么证明  1) D(X)=E(X^2)-[E(X)]^2  2) D(X)=E[X-E(X)]^2 证明如下所示：  这是一个数学统计的问题. D(X)指方差,E（x）指期望. E(X)说简单点就是平均值,具体做法是求和然后除以数量. D(X)就是个体偏离期望的差,再对这个差值进行的平方,最后求这些平方的期望.具体操作是,（个体-期望）,然后平方,再对这些平方值求平均值. 说清楚
随机变量的期望和方差
不二的博客
10-15 1万+
X服从两点分布，则  X服从超几何分布，即  ，则  X服从二项分布，即  ，则 X服从泊松分布，即  ，则 连续型 X服从均匀分布，即  ，则  ， X服从指数分布，即  ， 则  X 服从正态分布，即  ， 则  X 服从标准正态分布，即  ， 则    求正态分布的数学期望&&方差 设  ，求E（X），D（X）. 令  ，由于  ，所以  ，已知E...
期望， 方差， 协方差，标准差
四月晴
05-14 6万+
期望， 方差， 协方差，标准差 期望 概率论中描述一个随机事件中的随机变量的平均值的大小可以用数学期望这个概念，数学期望的定义是实验中可能的结果的概率乘以其结果的总和。 定义 设P(x) 是一个离散概率分布，自变量的取值范围为{x1,x2,...,xnx1,x2,...,xnx_1, x_2,..., x_n}。其期望被定义为： E(x)=∑k=1nxkP(xk)E(x)=∑...
7.4 期望值和方差
TROUBLE I AM IN
01-17 990
7.4 期望值和方差 期望值 E(X)=∑s∈Sp(s)X(s) E(X)=\sum_{s \in S}p(s)X(s) E(X)=s∈S∑​p(s)X(s) 例如一个点数从1到6的骰子，其投掷一次的期望值是 E(X)=1⋅16+2⋅16+3⋅16+4⋅16+5⋅16+6⋅16 E(X)=1 \cdot \frac{1}{6}+2 \cdot \frac{1}{6}+3 \cdot \frac{1}{6}+4 \cdot \frac{1}{6}+5 \cdot \frac{1}{6}+6 \cdot \fr
matlab 求期望和方差
05-30
假设有一个向量 `x`，则可以通过以下代码求其期望和方差： ```matlab % 求向量 x 的期望 mean_x = mean(x) % 求向量 x 的方差 var_x = var(x) ``` 如果要求矩阵的期望和方差，可以指定维度参数来求解。例如，假设...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值