时间序列学习笔记-1

Mushiyanu

已于 2024-11-10 14:52:46 修改

阅读量1k

点赞数 30

文章标签：学习笔记

于 2024-11-09 21:13:02 首次发布

本文链接：https://blog.csdn.net/Mushiyanu/article/details/143643790

版权

本笔记基于本人在学校课程中学习《时间序列分析》这门课程所记录。编程语言为R语言

本学习笔记任课参考老师的课件所制作，在此特别感谢我的老师。
本学习笔记参考北大李东风先生的《金融时间序列分析》授课备课资料，在此感谢。

可视化与探索性分析

对于任何数据分析工作而言，其入手的第一步就是尽可能将数据可视化。图示化数据可以清晰地展现数据的特征，包括数据的形态、异常值、随时间变化情况以及变量间的相互关系。我们在建模和预测时也应尽可能地将图中显示的特征纳入考虑。正如数据类型决定使用什么预测方法一样，数据类型也决定了使用什么图形来展示数据。
本笔记将介绍一些常见的时间序列图示工具，包括时间序列图，自相关图，季节图，散点图等。这些工具可以帮助我们快速了解序列的主要特征，随时间的变动模式。对于时间序列，通常的样本均值，样本方差等等这些常见的描述性统计量意义不大，有意义的是趋势性，季节性，相邻观测值之间的相关性等一些概念。
当然，在做任何分析之前，一定要确保你理解问题的实际背景，这实际上是对所有的统计建模的要求。要首先确保数据的收集没有问题，序列具有足够的长度，否则你不可能解决任何实际的问题。

时序图

时间序列分析的第一步就是绘制出时间序列图，即观测值对时间的连线图。时序图可以直观展示序列的重要特征，例如趋势性，季节性，异常点，以及变点等，了解这些特征有助于我们选择合理的模型，我们会在后面的例子里验证这一点。
在R中，plot()或者forecast::autoplot()函数应用于一个ts或者xts类型的时间序列对象就可以绘制出一个时间序列图；例如

library(ggplot2)
library(forecast)
TravelSky = read.csv("C:/Users/LuoLi/Desktop/TSA/data/data/TravelSky.csv",header = T)
head(TravelSky)
home = ts(TravelSky$domestic,start=c(2009,12),frequency = 12) 
# plot(home,type="o",main="中国民航订座量")
autoplot(home) +
  geom_point(col="red") +
  labs(title = "中国民航订座量") +
  theme(plot.title = element_text(hjust = 0.5))

在这里插入图片描述
这是中国民航信息网络公司月度公告所披露的中国民航业国内旅客订座量。这个时序图可以直观告诉我们如下信息：

订座量有长期显著增长的趋势；
年度内的订座量有明显的季节性特征，每年七八月份是出行高峰；
2020年后订座量大幅减少，显然这是受新冠疫情的影响；
于是，我们在后面进行预测建模时，就必须考虑这些因素，例如可以使用2020年之前的数据进行建模并预测，就可以定量评估疫情对航空业的影响幅度；在建模时，需要考虑趋势和季节因素，因此可以选取季节性ARIMA模型；要考虑假日影响的话，可以定义一个哑变量来表示假日，考虑ARIMAX模型。

ts 对象
ts 类型概述：

ts 是 R 中的规则时间序列类型，属于 stats 包。它适用于具有固定时间间隔的数据，如年度、季度或月度数据。
ts 对象有两个核心属性：start（起始时间）和 frequency（数据频率）。

频率的设置：

frequency 参数指定每年中的数据点数，例如：
年度数据（每年一个数据点）：frequency = 1
月度数据（每年12个数据点）：frequency = 12

因此，通过指定频率，可以灵活定义不同时间尺度的时间序列。

日数据的局限性：

对于金融数据的日数据，ts 类型可能不适用。金融市场在周末和节假日通常不交易，因此没有相应的数据记录。
ts 类型要求时间序列是连续的，即每一天都要有数据，不能直接从周五跳到周一。这种情况下，ts 类型不合适，因为它会强制时间序列无间断地跨越所有日期。
示例 - 创建年度和月度时间序列：
年度数据示例：
yd <- ts(c(4, 8, 7, 7, 3, 1, 8, 9, 8, 6, 3, 5, 5, 8, 2, 5, 9, 2, 5, 2, 3, 2, 2, 4), frequency = 1, start = 2001)
该时间序列表示从2001年开始的年度数据，每年一个数据点。
月度数据示例：
ym <- ts(c(9, 6, 3, 5, 4, 8, 2, 5, 8, 4, 6, 3, 2, 2, 6, 4, 1, 4, 2, 1, 8, 9, 4, 6), frequency = 12, start = c(2001, 1))
该时间序列表示从2001年1月开始的月度数据，每年12个数据点。
多元时间序列：

ts 函数可以将一个矩阵转换成多元时间序列，即同一时间点上有多个变量的数据。
ts.intersect 和 ts.union 函数可以合并两个或多个时间序列。ts.intersect 取时间段的交集，而 ts.union 取并集。
时间序列中的模式主要包括趋势性、季节性、周期性、非规则部分和假日效应等。在时间序列分析中，识别和分解这些模式是建模和预测的关键步骤。以下是对这些模式的详细解释：

时间序列中的模式

时间序列中的模式主要包括趋势性、季节性、周期性、非规则部分和假日效应等。在时间序列分析中，识别和分解这些模式是建模和预测的关键步骤。以下是对这些模式的详细解释：

季节性 (Seasonal)：
- 定义：季节性指的是时间序列在固定频率下出现的周期性波动。例如，销售数据可能因季节变化而波动，电风扇在夏季销量高而冬季低，公司盈利在年末受会计制度的影响可能高于年中。
- 记号：通常记为 $S_t$ ，表示由于季节因素引起的变化。
周期性 (Cyclic)：
- 定义：周期性是指时间序列中非固定频率的上升和下降模式。不同于季节性，周期性并没有固定的频率，例如美国经济的周期性扩张和收缩周期可以从3到10年不等。
- 注意：周期性和季节性不同之处在于其波动频率不固定。
- 记号：周期性可以和趋势性结合记为 $T_t$ 。
趋势 (Trend)：
- 定义：趋势是指时间序列长期内的平均水平变化。例如，全球气温可能在数十年内呈上升趋势。趋势可以被视为一种长时期的变化。
- 注意：趋势和周期的分界不一定明显，因此在实际分析中趋势和周期成分常被合并。
- 记号：趋势也记为 $T_t$ 。
非规则部分 (Irregular)：
- 定义：在剔除趋势、周期和季节性成分之后，剩下的波动部分是非规则的随机变动，通常被视为噪声或误差。
- 记号：记为 $I_t$ ，表示数据中不可预测的随机波动部分。
假日效应 (Holiday Effect)：
- 定义：假日效应或日历效应指的是特定日期（如周末或节假日）可能对时间序列产生影响。例如，在股市中，周末效应指一周的最后一个交易日的表现可能不同于其他交易日。
- 记号：假日效应记为 $D_t$ 。

模型表示

我们这里只主要考虑趋势、周期性、季节性以及非规则波动，即一个时间序列的波动主要地受这几种因素的影响，用数学记号可以表示为 $X_t = f(T_t, S_t, I_t)$ 。
实际中最常见的有加法模型假设和乘法模型假设：

加法模型： $X_t = T_t + S_t + I_t$
乘法模型： $X_t = T_t \cdot S_t \cdot I_t$

平稳时间序列

对于不具备趋势性和季节性，且波动恒定的时间序列，我们称之为平稳时间序列。平稳序列的分析与建模是时间序列分析的基础，通常作为后续章节的重点内容。
通过将时间序列分解为趋势、季节性和非规则成分，可以分别对这些成分进行估计和分析，从而构建更精确的时间序列模型。

季节图

我们可以通过forecast::ggseasonplot()函数来绘制季节图。季节图以季节作为横坐标，可以很清晰的显示季节形态。

home = window(home,end=c(2019,12))
ggseasonplot(home)+
  geom_point(col="red") +
theme(plot.title = element_text(hjust = 0.5))

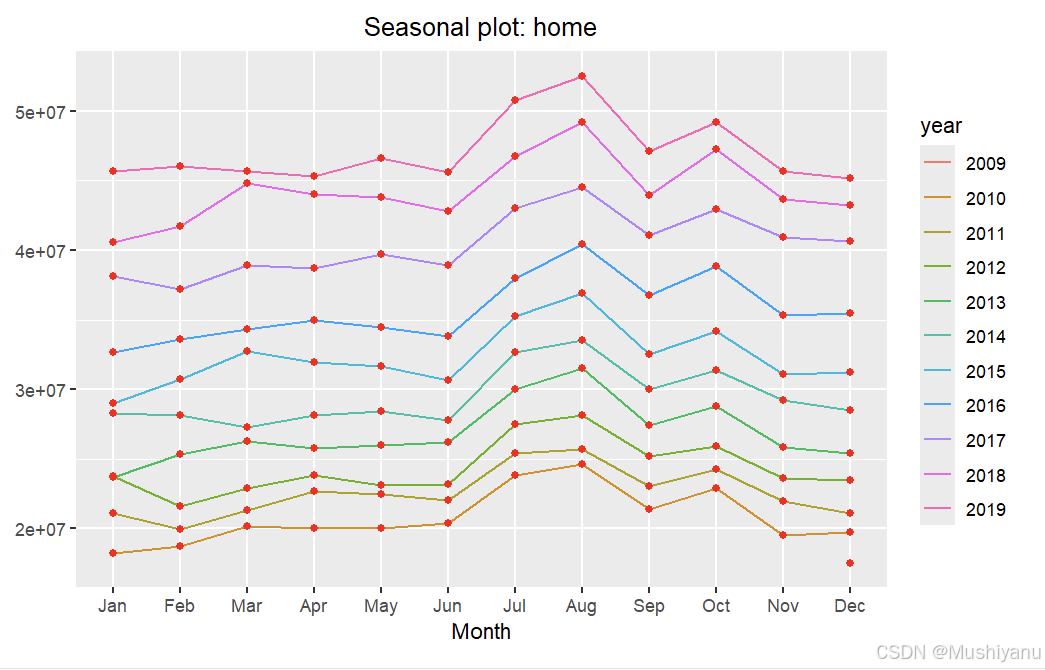
我们可以看到这些线没有交叉，呈现出很规律的随年份增长趋势。在同一年内，则显示出明显的季节性变动特点，从图可以知道每年的七八月份是出行的高峰。

季节图中可以将直角坐标转换为极坐标。设置参数polar=TRUE即可转化为极坐标，如下图所示。

home = window(home,end=c(2019,12))
ggseasonplot(home)+
  geom_point(col="red") +
theme(plot.title = element_text(hjust = 0.5))

ggseasonplot(home,polar=TRUE)

在这里插入图片描述

季节子序列图

我们可以通过forecast::ggsubseriesplot()函数着重描绘在相同季节数据的同比变化情况。

ggsubseriesplot(home)+
  geom_point(col="red")

在这里插入图片描述
图中的水平线表示每月的平均订座量。子系列季节图可以清晰的描绘出数据的潜在季节性形态，并且显示了季节性随时间的变化情况，这是观察季节性变化很有用的方式。

自相关图

1. 自相关系数

定义：自相关系数 $r_k$ 度量的是时间序列 ${ x_t \}$ 与其自身延迟 $k$ 个时间单位的值 ${ x_{t-k} \}$ 之间的相关性。
作用：就像相关系数度量两个变量之间的线性关系一样，自相关系数描述了序列内的每一项与之前项之间的相关性。这个度量非常重要，因为它揭示了数据是否具有时间依赖关系。
- 例如， $r_1$ 表示 $x_t$ 与 $x_{t-1}$ （前一项）之间的相关性。
- $r_2$ 表示 $x_t$ 与 $x_{t-2}$ （前两项）之间的相关性。
- 依此类推，通过不同的 $r_k$ 值，可以查看时间序列的不同滞后项之间的相关性。
计算公式：
自相关系数 $r_k$ 的计算公式为：
$r_k = \frac{\sum_{t=k+1}^{T} (x_t - \bar{x})(x_{t-k} - \bar{x})}{\sum_{t=1}^{T} (x_t - \bar{x})^2}$
- $\bar{x}$ 为时间序列 ${ x_t \}$ 的平均值。
- $T$ 是总的时间序列长度。
- 该公式描述了时间序列在滞后 $k$ 步的情况下与自身的相关程度。

2. 自相关函数图 (ACF)

定义：以滞后数 $k$ 为横坐标，自相关系数 $r_k$ 为纵坐标绘制的图称为自相关函数图，简称 ACF 图。
作用：ACF 图展示了时间序列随滞后数变化的自相关性模式，从而提供了对数据时间依赖性和周期性的一种可视化观察方式。这个图是时间序列分析中的一个重要工具，帮助我们识别数据中的趋势、季节性和周期性特征。
R 实现：在 R 语言中，可以使用 forecast::Acf 或 forecast::ggAcf 函数计算自相关系数并绘制 ACF 图。

set.seed(1)
WhiteNoise <- abs(rnorm(100))

# WhiteNoise 时间序列图
p1_time <- ggplot(data.frame(x = 1:100, y = WhiteNoise), aes(x, y)) +
  geom_line(color = "blue") +
  ggtitle("Time Series of WhiteNoise") +
  custom_theme +
  labs(x = "Time", y = "WhiteNoise")
# WhiteNoise 自相关图
p1_acf <- ggAcf(WhiteNoise) +
  ggtitle("ACF of WhiteNoise") +
  custom_theme +
  geom_hline(yintercept = 0, color = "darkgray") +
  scale_color_manual(values = c("blue"))

3. ACF 图的用途

自相关图能够揭示时间序列的一些重要特性，例如：

趋势：是否存在较长时间的持续上升或下降。
周期性或季节性：周期性的峰值或谷值，显示了数据的重复模式。
平稳性：当自相关图显示出逐渐衰减的趋势时，可能表示数据具有平稳性。

在这里插入图片描述

ACF图里的蓝色虚线值为 $\frac{2}{\sqrt{n}}$ ，是判断该滞后阶处自相关性是否显著的临界值；
上述四组图里，第一组有明显趋势，ACF衰减缓慢且值很大，这是因为观测点附近的值变化不大；
第二组同时有趋势和季节性，ACF不仅衰减缓慢(趋势的表现)且有圆齿状(季节周期性的表现)；
第三组只有4阶滞后的ACF显著，其余均不显著，这个序列没有前两个例子那样的明显趋势性和季节周期性；
第四组图是模拟的白噪声序列，其全部滞后的ACF都不显著，这正是白噪声序列的特点：无序列相关性。

偏自相关图和组合绘图

后面我们还会介绍另外一个图，叫偏自相关图(PACF)，forecast::Pacf或forecast::ggPacf可绘制PACF图。例如

ggPacf(AirPassengers)

在这里插入图片描述
R中，函数tsdisplay或forecast::ggtsdisplay可以一次性绘制时序图，ACF图和PACF图，在平稳时间序列建模时非常方便。

x <- AirPassengers |> log() |> diff()
ggtsdisplay(x)
# 这里的符号|>称为管道操作符，其含义是将其左侧函数的运算结果作为右侧函数的输入；有些书上用符号magrittr::%>%

在这里插入图片描述

散点图

当我们考虑两个时间序列之间的关系时，我们可以考虑两个变量之间的散点图，ggplot::geom_point() 用于绘制散点图。例如下面的例子

ggplot(data.frame(time = time(home), value = as.numeric(home)), aes(x = time, y = value)) +
  geom_point(color = "red") +  # 使用红色点
  ggtitle("中国民航订座量") +  # 图表标题
  theme(plot.title = element_text(hjust = 0.5)) +  # 标题居中
  labs(x = "时间", y = "订座量")  # 设置坐标轴标签

在这里插入图片描述