二分图判定和匈牙利算法

1.染色法判定二分图 O(n+m)

重要性质： 1.一个图是二分图，当且仅当（<=>）图中不含奇数环（环当中的边数是奇数）

        2.一个图不含奇数环，则一定是二分图

证明参考链接

二分图：一个图中的所有点能被划分在两个集合中，它们之前的边都不存在于集合内，而是在集合之间

• 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。
  

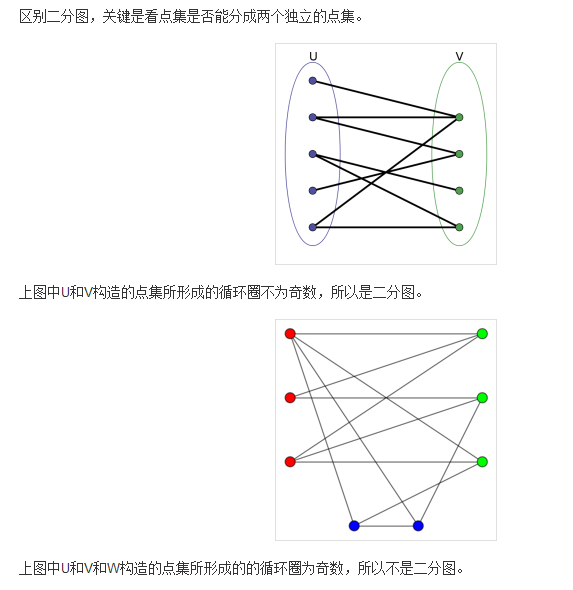
二分图染色

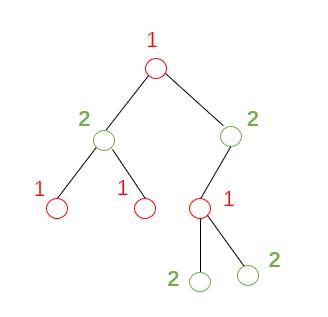
由于图中不含奇数环，所以染色过程中一定没有矛盾

反证法：假设染色过程中出现了矛盾。

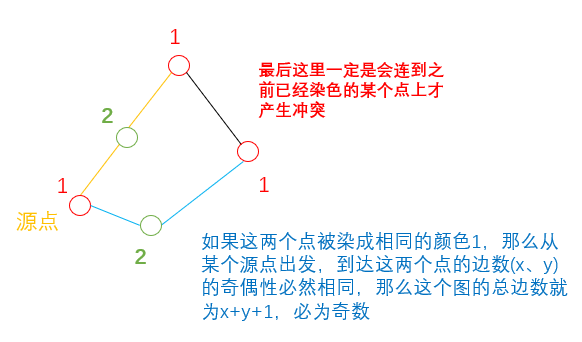
所以染色过程中一旦出现了矛盾，就一定存在奇数环。

可以通过dfs去判断染色是否会出现矛盾=>是否存在奇数环=>是否是二分图

注意：二分图不一定是连通的 ，只要能将所有点分成两个集合，使得所有边只出现在集合之间即可

所以要在主函数中加一重循环

基本思路

for(int i=1;i<=n;i++)
	if i 未染色
		dfs(i,color)//就通过dfs给它染色

例题

“包含自环、重边”的描述，是为了告诉大家算法本身可以有效处理这种边界问题，如果有自环的话，就会发现自环这条边的两端颜色相同，就矛盾了。

输入

4 4
1 3
1 4
2 3
2 4

输出

Yes

代码

#include <iostream>
#include <queue>
#include <cstring>
#include <algorithm>
const int maxn=1e5+5;
const int INF=0x3f3f3f3f;
using namespace std;
int n,m;
int h[maxn],e[2*maxn],nex[2*maxn],idx;//注意存边的时候要扩大一倍，因为要存储双向边
int color[maxn];//存储该结点被染的颜色
void add(int a,int b)
{
	e[idx]=b;
	nex[idx]=h[a];
	h[a]=idx++;
}
bool dfs(int k,int c)
{
	color[k]=c;//染色
	for(int i=h[k];i!=-1;i=nex[i])//遍历一下当前结点的所有邻结点
	{
		int j=e[i];
		if(!color[j])//如果当前没有被染色
		{
			if(!dfs(j,-c))//染色记号为1或2，就用1+2-c，染色记号为1或-1就直接取负就可以
			return false;//要这样递归的去看之后的结点会不会产生矛盾
		}
		else if(color[j]==c)//本身可以处理掉有自环的情况
			return false;
	}
	return true;
}
int main()
{
	cin>>n>>m;
	memset(h,-1,sizeof(h));//一开始忘记初始化了，会导致结果错误
	for(int i=0;i<m;i++)
	{
		int a,b;
		cin>>a>>b;
		add(a,b);
		add(b,a);//无向图
	}
	bool flag=true;
	for(int i=1;i<=n;i++)//因为二分图可能是不连通的，然后要保证每个连通分量都被着色
	{
		if(!color[i])//如果这个点没有被染色
		{
			if(!dfs(i,1))//如果dfs染色失败
			{
				flag=false;
				break;
			}
		}
	}
	if(flag)
	cout<<"Yes"<<endl;
	else
	cout<<"No"<<endl;
	return 0;
}

2.匈牙利算法 O(mn)，但实际运行时间一般远小于这个

基本思路

匈牙利算法用来找二分图的最大匹配


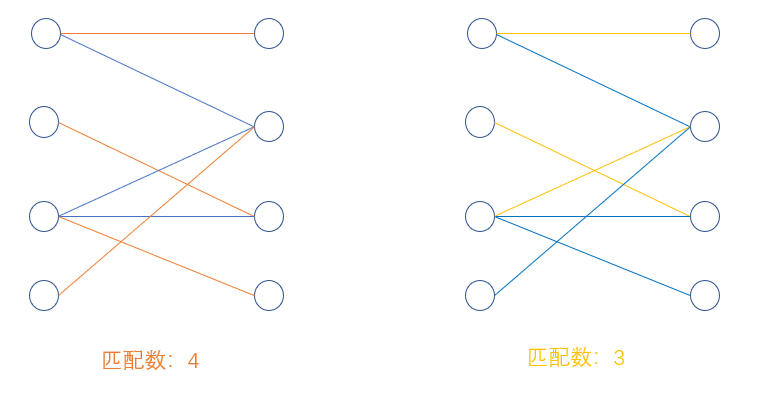
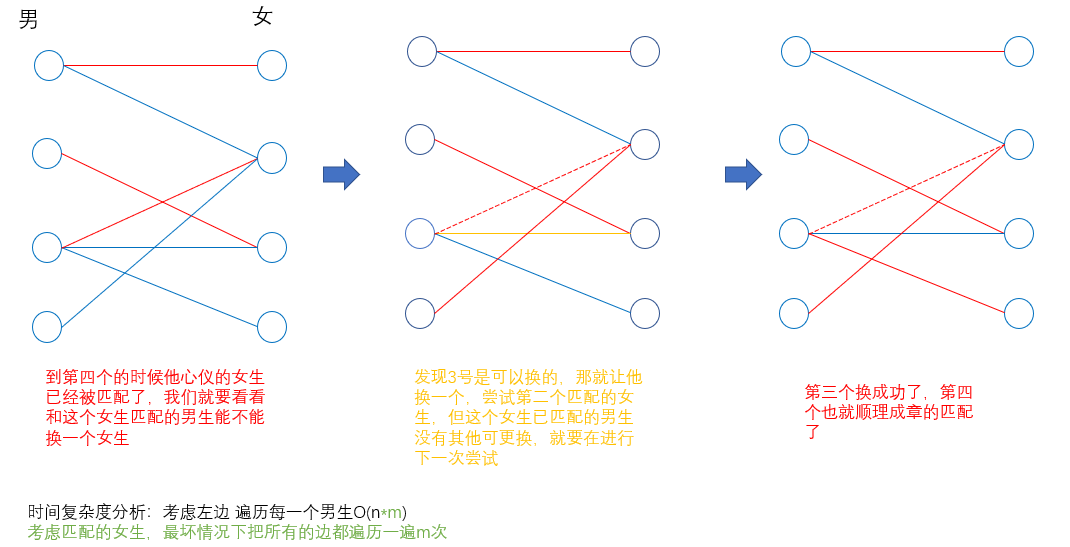
算法证明参照《算法导论》

例题

题目保证了是二分图

输入

2 2 4
1 1
1 2
2 1
2 2

输出

2

代码

数组尽量开大一点，如果数组越界，什么问题都能发生，不仅仅是段错误

注意这里只要存从左边到右边方向即可，因为是遍历男生去找匹配的，且两个点集的编号是重合的如果再add(2,1)有可能多了一条边会造成错误。

#include <iostream>
#include <queue>
#include <cstring>
#include <algorithm>
const int maxn=1e5+5;
const int INF=0x3f3f3f3f;
using namespace std;
int n1,n2,m;
int h[maxn],e[2*maxn],nex[2*maxn],idx;//注意存边的时候要扩大一倍，因为要存储双向边
int match[maxn];//存储女生所匹配的男生
bool st[maxn];//标记女生有没有被考虑过（即这个点有没有被访问过）
void add(int a,int b)
{
	e[idx]=b;
	nex[idx]=h[a];
	h[a]=idx++;
}
bool find(int x)
{
	for(int i=h[x];i!=-1;i=nex[i])//枚举这个男生心仪的女生
	{
		int j=e[i];
		if(!st[j])//j没有被访问过
		{
			st[j]=true;
			if(!match[j]||find(match[j]))//女生没有匹配的男生或女生所匹配的男生能够换一个女生匹配
			{
				match[j]=x;//就让这个女生和现在这个男生匹配
				return true;
			}
		}
	}
	return false;
}
int main()
{
	cin>>n1>>n2>>m;
	memset(h,-1,sizeof(h));//一开始忘记初始化了，会导致结果错误
	for(int i=0;i<m;i++)
	{
		int a,b;
		cin>>a>>b;
		add(a,b);//因为遍历男生去找匹配的女生即可，所以只要存储左边到右边方向即可
		//add(b,a);//无向图
	}
	int ans=0;
	
	for(int i=1;i<=n1;i++)
	{
		fill(st,st+maxn,false);//注意这个st数组初始化的位置，如果放在循环外会出错
		if(find(i))
		ans++;
	}
	cout<<ans<<endl;
	return 0;
}

st数组用来判重，避免在某次匹配中重复遍历点和边

st数组用来防止重复搜索相同的点。当图中有环的时候，不加st数组可能会无限循环下去，就出现段错误了

• “不加st数组的话，如果遇到偶数长度回路(双向边)的话就会陷入递归死循环。对于为什么加入st数组仍然可以保证答案正确，首先每次为一个点做匹配时，都会将st数组全部初始化为false，即find函数是为把当前这个点匹配出去而进行尝试。下面分为三种情况，第一种，直接匹配成功，显然与st数组没什么关系；第二种，第一次想要匹配的点已经被匹配过了，但是通过递归调换最后匹配成功，同样st数组不会影响答案；第三种，设当前正在尝试与可以和它进行匹配的第k个点进行匹配，之前k-1个可以与它匹配的点的匹配尝试均失败，在递归调换的过程中某个点遇到了被标记的点，那么说明与这个点匹配的点无法做出”妥协”，所以就可以不必在从这个被标记的点在往下尝试。这样可以保证每个点只会被被递归访问一次，那么每条边也只会被访问一次，从而可以保证匈牙利算法的复杂度上限为O(NM)。”
• “1.经过测试，若不加st数组，MLE,应该是爆栈了。所以必须要加 2.虽然我们看for (int i = h[x]; i != -1; i = ne[i])，的确对于x只会遍历x的所有邻边且一次，遍历完后自然就结束了，但是st这里还有个作用，作为递归以防死循环。
  –>  eg:比如当前层：x尝试找j女生，然后j女生已经匹配，那么递归到下一层。我们尝试math[j]的男生去匹配，假如math[j]的男生也去找j女生(这个j女与上一层女生同一人)，那么尴尬了与上一层x尝试找j女生的情况等价，那么再递归找math[j]…显然死循环了。这里只是说一种st必须存在的必要性，较局限。”