数学建模——多元分析（1）——聚类分析

一、聚类分析

1. 概述

1. 聚类分析（cluster analyses）可作为一种定量方法，从数据分析的角度，给出一个准确、细致的分类工具。

2. 相似性度量

2.1. 样本的相似性度量

1. 重点内容

1. 核心思想：用距离来度量样本点间的相似程度。距离近的样品聚为一类。
   
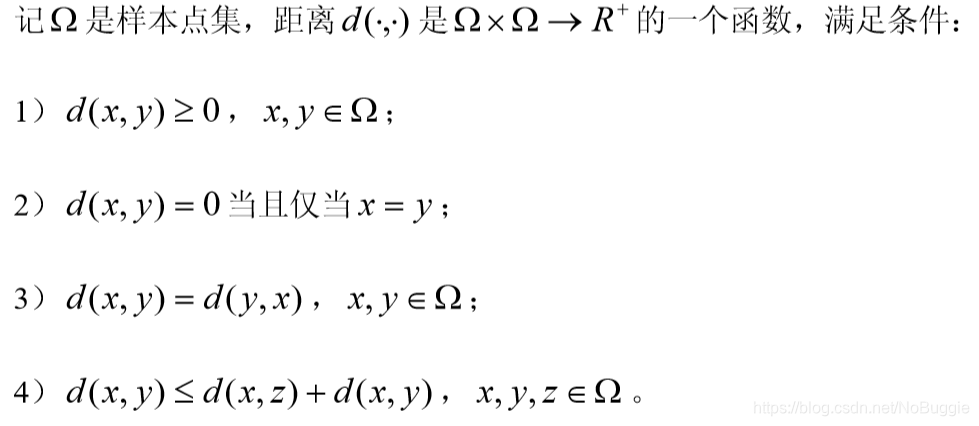
2. 在聚类分析中，对于定量变量，常用的是 Minkowski 距离
   
   
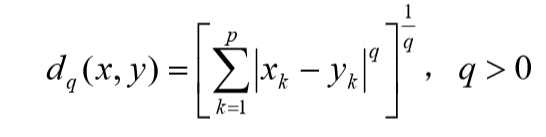
3. 在 Minkowski 距离中，常用的是欧氏距离，它的主要优点是当坐标轴进行正交旋转时，欧氏距离是保持不变的。因此，如果对原坐标系进行平移和旋转变换，则变换后样本点间的距离和变换前完全相同。
4. 采用 Minkowski 距离时，一定要采用相同量纲的变量。如果变量的量纲不同，测量值变异范围相差悬殊时，建议首先进行数据的标准化处理，然后再计算距离。
5. 在采用 Minkowski 距离时，还应尽可能地避免变量的多重相关性。多重相关性(multicollinearity)所造成的信息重叠，会片面强调某些变量的重要性。
6. 由于 Minkowski 距离的这些缺点，一种改进的距离就是马氏距离，定义如下：
   
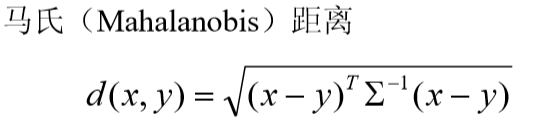
   其中x, y为来自p 维总体Z的样本观测值，Σ为Z的协方差矩阵，实际中Σ往往是不知道的，常常需要用样本协方差来估计。马氏距离对一切线性变换是不变的，故不受量纲的影响。
7. 此外，还可采用样本相关系数、夹角余弦和其它关联性度量作为相似性度量。

2. 示例

下