在主成分分析系列(一)概览及数据为何要中心化这篇文章中介绍了PCA算法的大概想法及数据为何要中心化,在这篇文章具体推导PCA算法的过程。
1. 首先 PCA 最原始的想法是:
-
设 V \mathbf{V} V 为 d {d} d 维 线性空间(即 R d \mathbb{R}^d Rd), W \mathbf{W} W 为 V \mathbf{V} V 的 k k k 维线性子空间( k < d k<d k<d)。在 W \mathbf{W} W 中找到数据 D = { x 1 , x 2 , … x n } \mathbf{D}=\{ \mathbf{x_1},\mathbf{x_2},\dots \mathbf{x_n} \} D={x1,x2,…xn} 最准确的表达。 x i ∈ R d , i = 1 , … , n \mathbf{x_i} \in \mathbb{R}^d, i = 1,\dots,n xi∈Rd,i=1,…,n
-
一组 d d d 维向量 { e 1 , e 2 , … , e k } \{\mathbf {e_1,e_2,…,e_k}\} {e1,e2,…,ek},它形成 W \mathbf {W} W的一组正交基 。在 W \mathbf{W} W空间中的任何向量都可以被表示为 ∑ i = 1 k α i e i \sum_{i=1}^{k}\alpha_i \mathbf{e}_{i} ∑i=1kαiei
-
那么向量 x 1 \mathbf{x_1} x1可以被表示为
∑ i = 1 k α 1 i e i \sum_{i=1}^{k}\alpha_{1i} \mathbf{e}_{i} i=1∑kα1iei -
针对向量 x 1 \mathbf{x_1} x1,误差为
e r r o r = ∥ x 1 − ∑ i = 1 k α 1 i e i ∥ 2 \mathbf{error} = \Vert \mathbf{x_1}-\sum_{i=1}^{k}\alpha_{1i} \mathbf{e}_{i} \Vert^2 error=∥x1−i=1∑kα1iei∥2
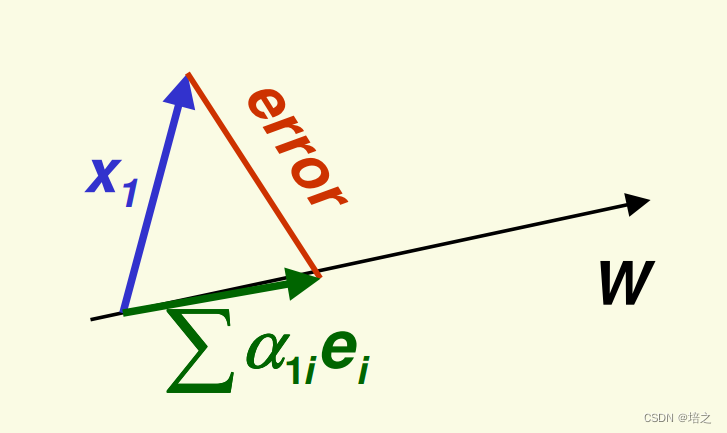
所以,接下来,我们要把所有的 e r r o r \mathbf{error} error 加和,每个 x j \mathbf{x_j} xj 可以表示为
x j = ∑ i = 1 k α j i e i \mathbf{x_j}=\sum_{i=1}^{k}\alpha_{ji} \mathbf{e}_{i} xj=i=1∑kαjiei
那么所有的误差是:

为了求得
J
\mathbf{J}
J 的最小值,我们需要求相关的偏导数,也需要限制
{
e
1
,
e
2
,
…
,
e
k
}
\{\mathbf {e_1,e_2,…,e_k}\}
{e1,e2,…,ek}是正交向量。
2. 让我们先化简 J \mathbf{J} J的表达:
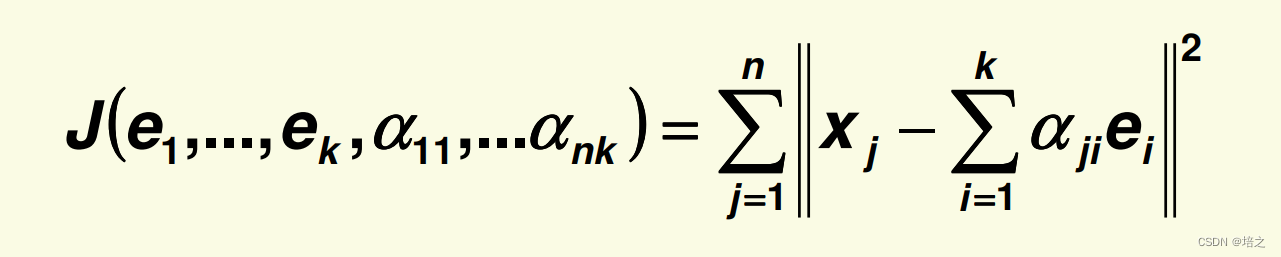
注意,下面
x
j
t
\mathbf{x_j}^t
xjt 右上角的 t 表示向量的转置。
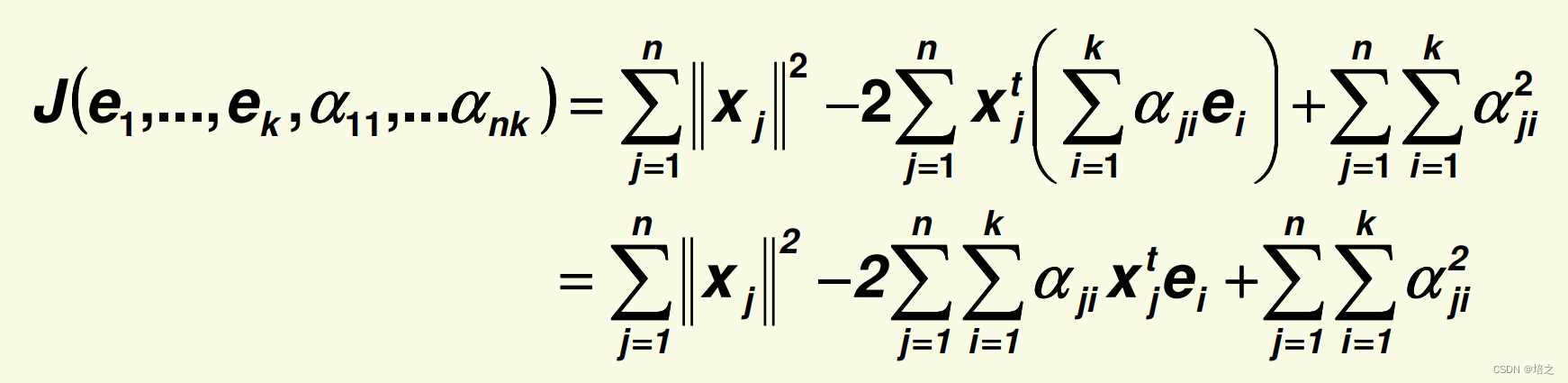
3. 求偏导
对
α
∗
∗
\alpha_{**}
α∗∗ 求偏导,
α
∗
∗
\alpha_{**}
α∗∗的下标取
m
l
ml
ml,即
α
m
l
\alpha_{ml}
αml
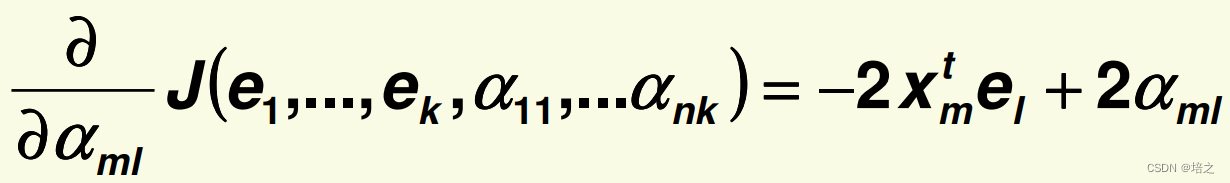
因此,针对
α
m
l
\alpha_{ml}
αml 的最优点是
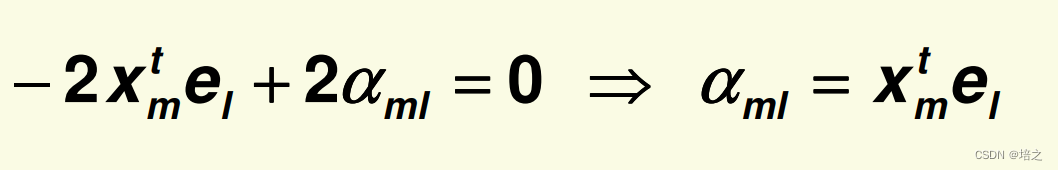
将
α
m
l
=
x
m
t
e
l
\alpha_{ml}=\mathbf{x_m}^t\mathbf{e_l}
αml=xmtel回代
J
\mathbf{J}
J的表达式
得到

得到

将
J
\mathbf{J}
J 表达式的后半部分 重写成下面的形式
(
a
t
b
)
2
=
(
a
t
b
)
(
a
t
b
)
=
(
b
t
a
)
(
a
t
b
)
=
b
t
(
a
a
t
)
b
(\mathbf{a}^{t}\mathbf{b})^{2}=(\mathbf{a}^{t}\mathbf{b})(\mathbf{a}^{t}\mathbf{b})=(\mathbf{b}^{t}\mathbf{a})(\mathbf{a}^{t}\mathbf{b})=\mathbf{b}^{t}(\mathbf{a}\mathbf{a}^{t})\mathbf{b}
(atb)2=(atb)(atb)=(bta)(atb)=bt(aat)b
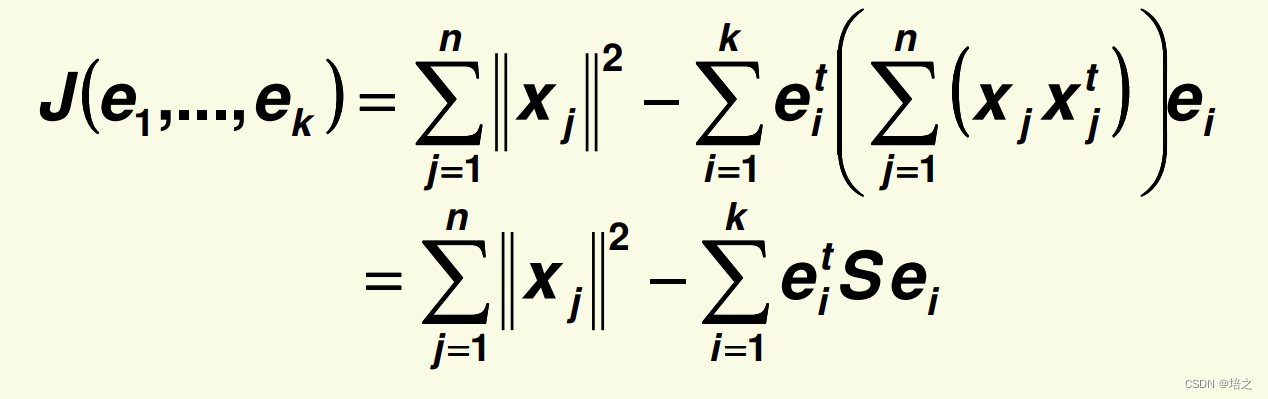
其中,
S
\mathbf{S}
S 等于
S
=
∑
j
=
1
n
x
j
x
j
t
\mathbf{S}=\sum_{j=1}^{n}\mathbf{x}_j\mathbf{x}_j^t
S=j=1∑nxjxjt
S
\mathbf{S}
S 被称为 scatter 矩阵,它只不过是
n
−
1
n-1
n−1乘上样本协方差矩阵
Σ
^
\hat{\Sigma}
Σ^:
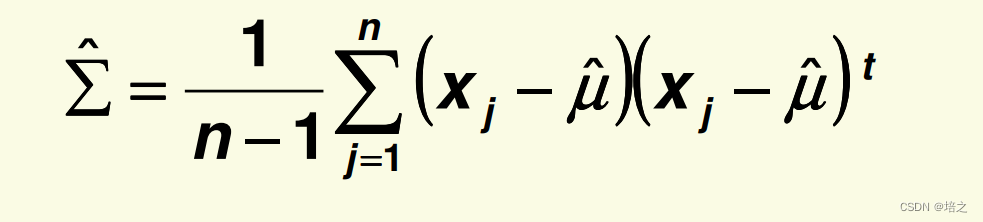
此时,
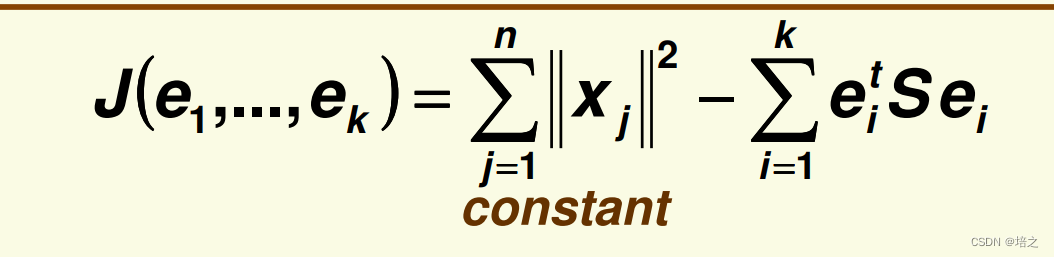
那么最小化
J
\mathbf{J}
J 等价于最大化

4. 拉格朗日乘子法
同时,因为前文假设
e
i
\mathbf{e_i}
ei是正交单位向量, 也要限制所有
e
i
t
e
i
=
1
,
i
=
1
,
…
,
n
\mathbf{e}_{i}^t\mathbf{e}_{i} =1 ,\quad i=1,\dots,n
eitei=1,i=1,…,n
使用拉格朗日乘子法,对所有的限制使用相应的
λ
1
,
…
,
λ
k
\lambda_1,\dots,\lambda_k
λ1,…,λk
现在,我们需要最小化新的优化函数

求关于
e
m
\mathbf{e}_m
em的所有的偏导数:
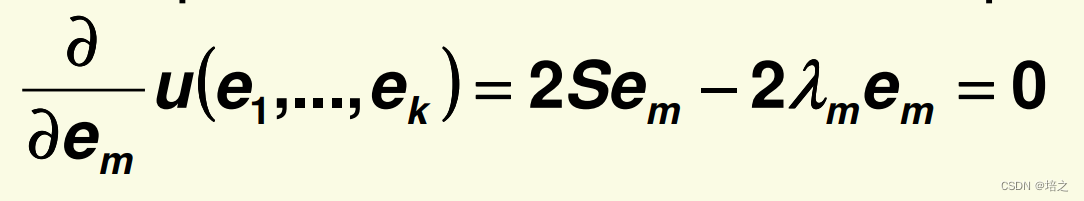
所以,
λ
m
\lambda_m
λm 跟
e
m
\mathbf{e}_m
em 分别是 scatter矩阵
S
\mathbf{S}
S的特征值与特征向量。
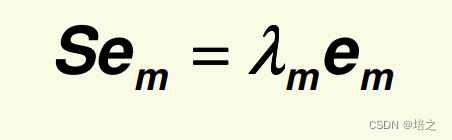
将
e
m
\mathbf{e}_m
em 回代下式
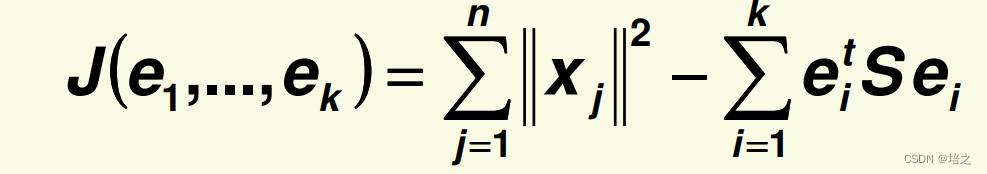
而且使用推导结论:
S
e
m
=
λ
m
e
m
\mathbf{S}\mathbf{e}_m=\lambda_m\mathbf{e}_m
Sem=λmem
可以得到
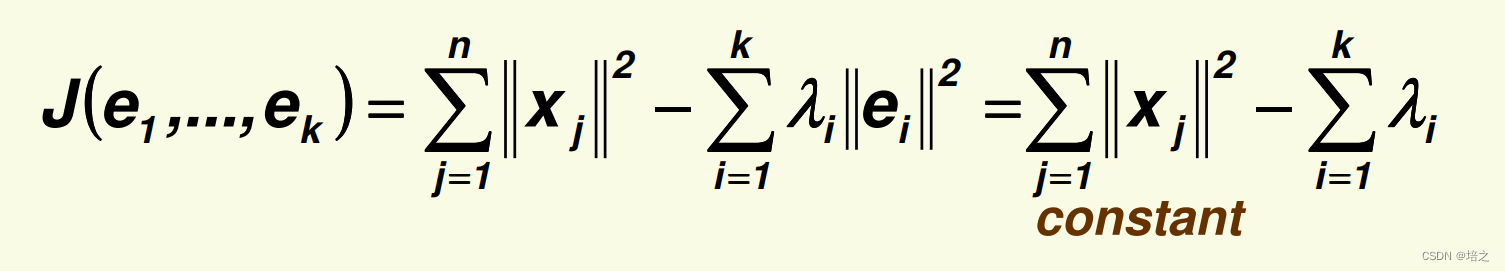
因此,为了最小化
J
\mathbf{J}
J,将
S
\mathbf{S}
S的
k
k
k 个特征向量对应于
k
k
k 个最大特征值作为
W
\mathbf{W}
W 的基底。
- S \mathbf{S} S的特征值越大,对应特征向量方向的方差越大。注意,这个结论还没证明,在主成分分析系列(三)为何协方差矩阵的特征值越大对应的特征向量方向的方差越大给出证明,先假设这个结论是正确的。
直观地,从在主成分分析系列(一)概览及数据为何要中心化这篇文章中例子来看,

这个结果正是我们所期望的:将
x
\mathbf{x}
x 投影到方差最大的
k
k
k 维子空间中
这是非常直观的:将注意力限制在分散最大的方向上。
因此,PCA 可以被认为是通过旋转旧轴(因为轴需要满足过原点,相互正交地限制)来寻找新的正交基,直到找到最大方差的方向。
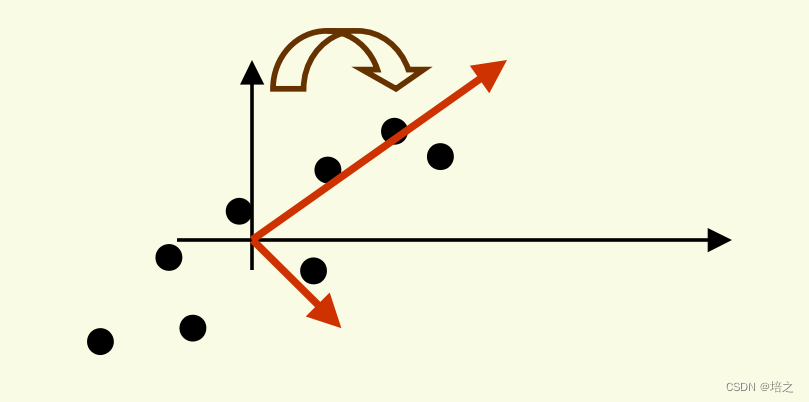
5.PCA用作数据逼近
令
{
e
1
,
e
2
,
…
,
e
d
}
\{\mathbf {e_1,e_2,…,e_d}\}
{e1,e2,…,ed}是 scatter 矩阵
S
\mathbf{S}
S 的所有特征向量,并且是按照它们对应的特征值大小降序排列的。那么
不需要任何近似,任何的样本
x
i
\mathbf{x_i}
xi都能写成
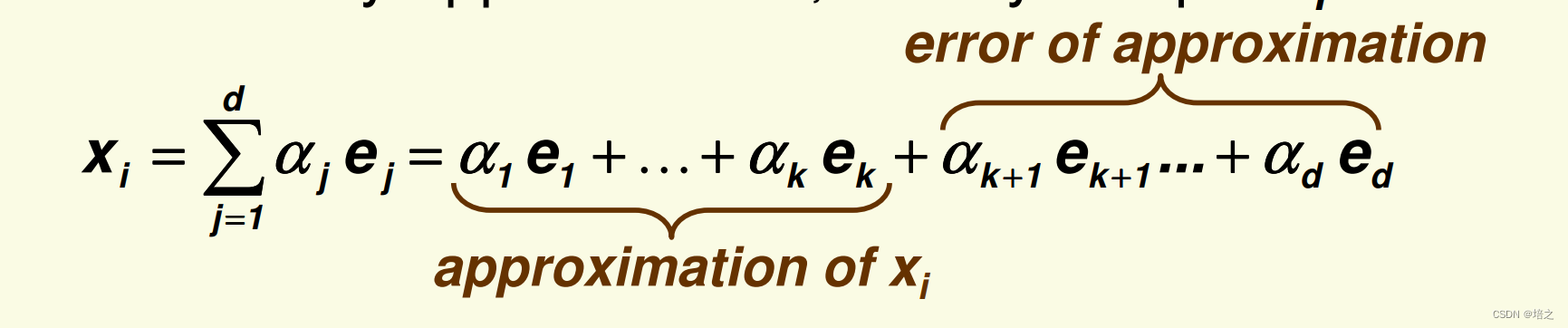
系数
α
m
=
x
i
t
e
m
\alpha_m=\mathbf{x}_i^{t}\mathbf{e}_m
αm=xitem被称作主成分(principle component )
- k k k 越大,近似越好
- 成分是按照重要性排序的,越重要的越放在前面。
因此 PCA 将 x i \mathbf{x}_i xi 的前 ¥k$ 个最重要的分量作为 x i \mathbf{x}_i xi的近似值
6.最后一步
现在我们已经知道如何投影数据,最后一步是改变坐标以获得最终的
k
k
k维向量
y
\mathbf{y}
y
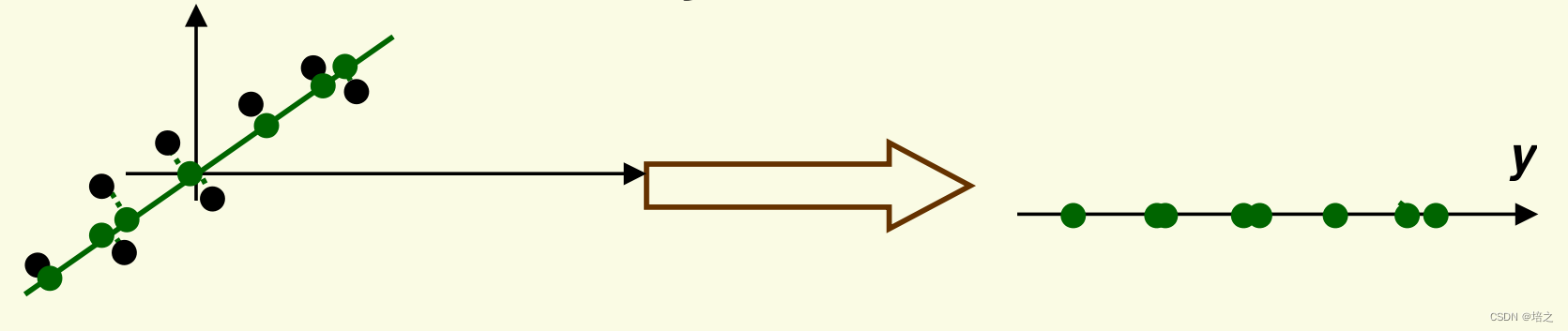
令矩阵
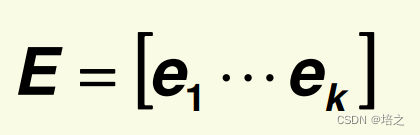
则坐标变换是
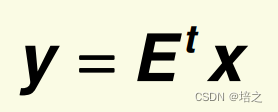
在
E
t
\mathbf{E}_t
Et 下,特征向量成为标准基:
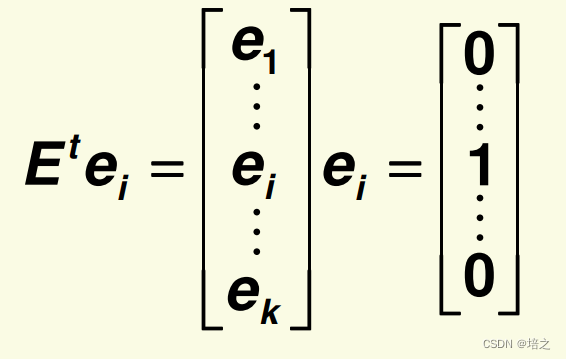
7. PCA算法的流程

8. PCA算法的例子


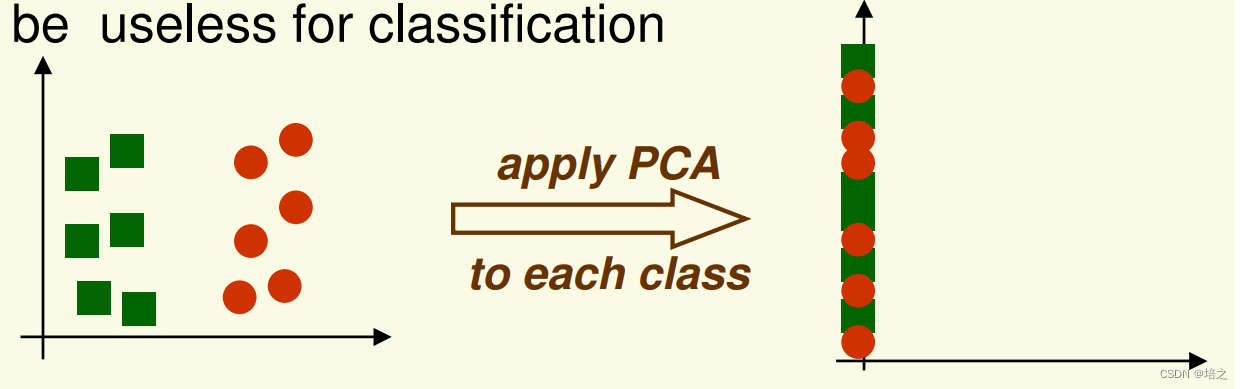
9. PCA 算法的缺点
- PCA 旨在准确表示数据,而不是数据分类。
- 然而,最大方差的方向对于分类可能是无用的
参考文献
Introduction to Statistical Machine Learning
Lecture 2
Anders Eriksson
School of Computer Science
University of Adelaide, Australia























 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










