TensorFlow+深度学习笔记2

最新推荐文章于 2022-05-15 12:11:11 发布

Alvin's Tech Blog

最新推荐文章于 2022-05-15 12:11:11 发布

阅读量529

点赞数

分类专栏：深度学习文章标签：深度学习 TensorFlow Deep CNN LeNet mnist

本文链接：https://blog.csdn.net/Pan_Chengyuan/article/details/79967841

版权

深度学习专栏收录该内容

7 篇文章 0 订阅

订阅专栏

TensorFlow+深度学习笔记2

标签（空格分隔）：TensorFlow+深度学习笔记

本周掌握的知识：

深度学习基本概念理解：Linear regression、Logistic regression、Softmax。并使用python完成对应代码实现；
在课件的指导下，参考示例实现了Deep CNN, 最终的识别率达到99.35%；
了解了LeNet，参考《Tensorflow实战Google深度学习框架》的代码参数实现了LeNet来解决 mnist 数字识别问题，最终识别率达到98.79%

Task 2 使用TensorFlow

1 学习清单

深度学习基本概念理解：Linear regression、Logistic regression、Softmax。
理解 CNN，并用简单 CNN 解决 mnist 数字识别问题
了解 LeNet

2 参考资料

上述内容参考资料均可在 task-1 文档的参考资料找到。
简单 CNN 可以是《香港科技大学 TensorFlow 三天速成课件》—《TF-UST
DAY2.pptx》— P84 的结构：

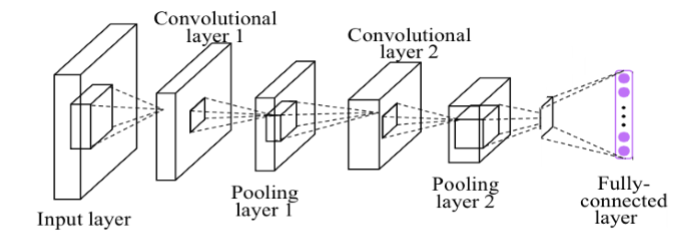
3 周报内容

Linear regression、Logistic regression、Softmax：解释对这几个概念的理解，
同时编程实现，并贴出代码以及运行结果
解释 CNN 每一个层的功能、具体如何实现（比如卷积是怎么做的、pooling
怎么做、fully connected 怎么做）、每个参数对应的意义。同时编程解决 mnist
数字识别问题，尽可能解释每一句关键代码的意义，贴上实验结果。
解释 LeNet 每一个层的功能、具体如何实现、每个参数对应的意义。同时编
程解决 mnist 数字识别问题，尽可能解释每一句关键代码的意义，贴上实验
结果。

1 深度学习基本概念理解

Linear regression

线性回归分为一元线性回归和多元线性回归，首先来理解一元的情况：

假设有很多数据点（红色×），我们利用这些数据集得到绿色的直线：
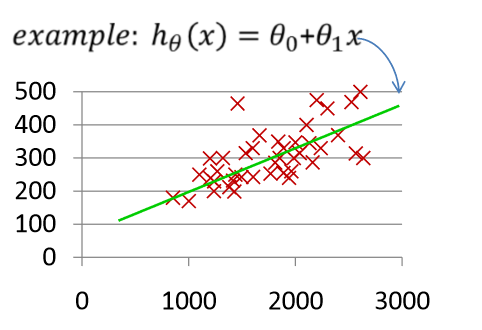
1.png-24.6kB

得到的回归方程h可以用来预测（输入数据点，输出预测值）
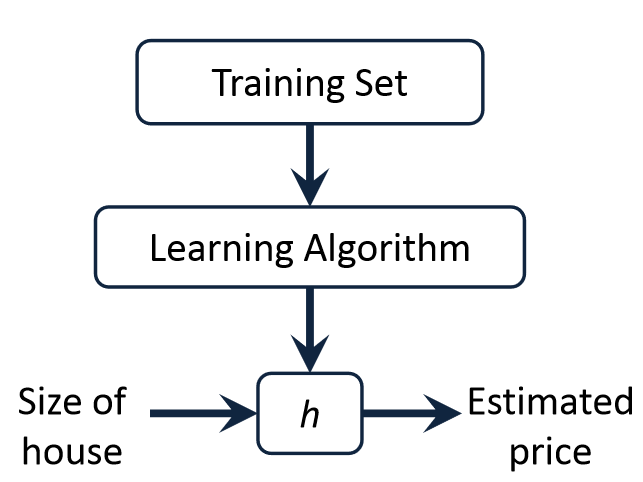
2.png-19kB

那么如何得到这条绿色直线？我们定义一个Cost Function，然后使得求得的直线让Cost Function的值最小：
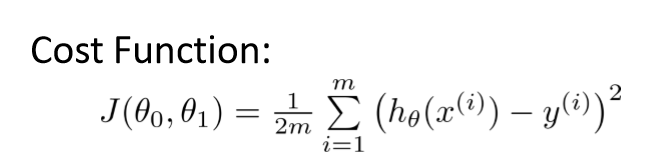
1.png-16.4kB

首先先假设h的各个参数，然后通过梯度下降法逐步更新参数，当损失函数达到全局最小的时候这些参数就是我们需要的参数：
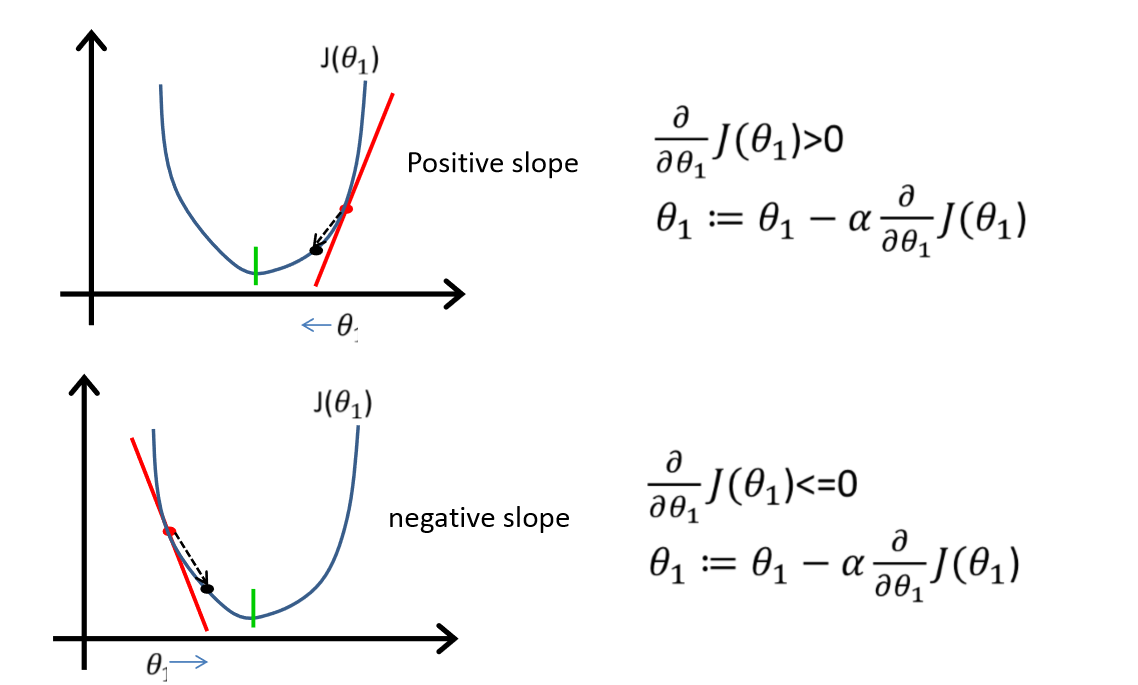
1.png-71.3kB

总的来说，一元线性回归的过程和目标如下：
1.png-61.6kB

多元的情况类似，就是数据集的自变量是多元的，举个例子来说：如果一元的情况是在研究数学成绩和物理成绩的关系，那么多元的情况就是研究数学成绩和物理、化学、生物、语文等科目的关系。

总的来说，多元线性回归的过程如下（目标也是使得Cost Function全局最小）：
1.png-81.8kB

需要注意的问题:
1 学习率α的选择。如果α太小，梯度下降的收敛速度会变得很慢；如果α太大，梯度下降算法可能不会收敛甚至会发散。如下图（第一张是α的取值太小，第二张是α取值太大）：
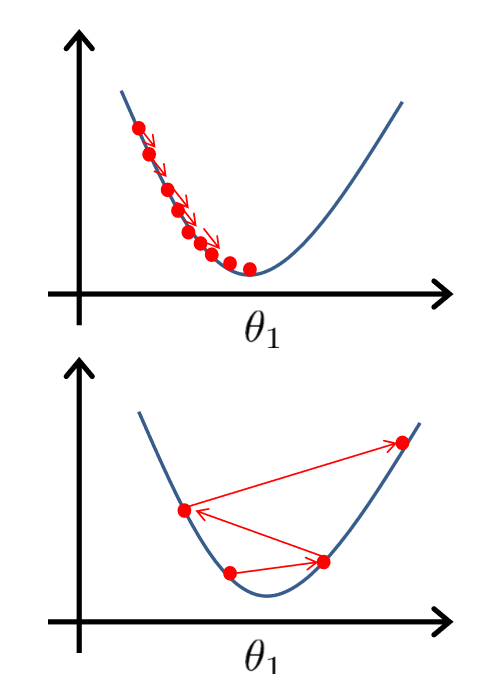
1.png-19.9kB

2 对于多元线性回归，除开注意α取值，还要注意Feature Scaling问题。比较常见的方法如下：
1.png-45kB
面对多维特征问题的时候，要保证特征具有相近的尺度，这将帮助梯度下降算法更快地收敛。解决的方法是尝试将所有特征的尺度都尽量缩放到-1 到 1 之间，最简单的方法就是(X - mu) / sigma，其中mu是平均值， sigma 是标准差。

3 对于多元线性回归，可以使用梯度下降算法求θ向量，也可以使用Normal Equation：
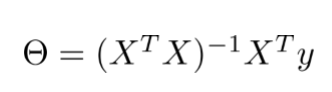
1.png-6.4kB

两种方法的区别：
1.png-65.4kB

多元线性回归代码实现：

    # coding: utf-8
    import random
    import numpy as np
    import matplotlib.pyplot as plt

    # 加载数据
    def load_data(filename):
        data = []
        with open(filename, 'r') as f:
            for line in f.readlines(): 
                line = line.split(',')
                currentitem = [int(item) for item in line]
                data.append(currentitem)
        return data

    # 特征缩放
    def feature_scaling(X):
        X_norm = X;
        colnum = X.shape[1]
        mu = np.zeros((1, colnum))
        sigma = np.zeros((1, colnum))
        for i in range(colnum):
            mu[0,i] = np.mean(X[:,i]) # 均值
            sigma[0,i] = np.std(X[:,i]) # 标准差
        X_norm  = (X - mu) / sigma
        return X_norm,mu,sigma

    # 梯度下降
    def gradient_descent(X, y, theta, alpha, num_iters):
        m = y.shape[0]
        J_history = np.zeros((num_iters, 1))
        for iter in range(num_iters):
            theta = theta - (alpha/m) * (X.T.dot(X.dot(theta) - y))
            J_history[iter] = compute_cost(X, y, theta)
        return J_history,theta

    # 计算损失
    def compute_cost(X, y, theta):
        m = y.shape[0] 
        differ = X.dot(theta) - y
        J = (differ.T.dot(differ))/ (2*m)
        return J

    # 预测
    def predict_value(data, mu, sigma, theta):
        testx = np.array(data)
        testx = ((testx - mu) / sigma)
        testx = np.hstack([testx,np.ones((testx.shape[0], 1))])
        price = testx.dot(theta)
        return price

    # 初始化数据
    iterations = 500
    alpha = 0.01
    theta = np.zeros((3, 1))

    # 加载数据
    data = load_data('train_data.txt')
    data = np.array(data,np.int64)

    # 赋值参数
    x = data[:,(0,1)].reshape((-1,2))
    y = data[:,2].reshape((-1,1))
    m = y.shape[0]

    # Feature Scaling
    x,mu,sigma = feature_scaling(x)

    # 计算损失值
    X = np.hstack([x,np.ones((x.shape[0], 1))])
    j = compute_cost(X,y,theta)

    # 梯度下降算法
    J_history,theta = gradient_descent(X, y, theta, alpha, iterations)

    # 输出结果
    print("The theta results are:")
    print(theta)

    # 预测
    predict_data = load_data('test_data.txt')
    predict_data = np.array(predict_data, np.int64)
    test_x = predict_data[:,(0,1)].reshape((-1,2))
    test_y = predict_data[:,2].reshape((-1,1))
    results = predict_value(test_x, mu, sigma, theta)
    print('The true price are:')
    print(test_y)
    print('The predict price are:')
    print(results)

    # 绘制迭代收敛图
    plt.plot(J_history)
    plt.ylabel('loss')
    plt.xlabel('iteration numbers')
    plt.title('Loss graph')
    plt.show()

实验结果如下：
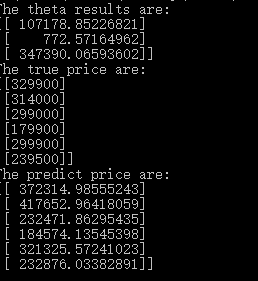
2.png-4.9kB
可以看到预测的结果和实际结果不大
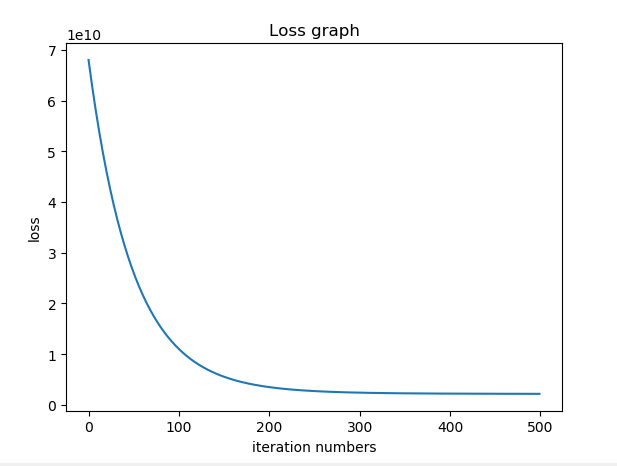
1.png-17.2kB
迭代在100~200之间就差不多收敛了
数据集：
train_data.txt文件里面的数据如下：

2104,3,399900
1600,3,329900
2400,3,369000
1416,2,232000
3000,4,539900
1985,4,299900
1534,3,314900
1427,3,198999
1380,3,212000
1494,3,242500
1940,4,239999
2000,3,347000
1890,3,329999
4478,5,699900
1268,3,259900
2300,4,449900
1320,2,299900
1236,3,199900
2609,4,499998
3031,4,599000
1767,3,252900
1888,2,255000
1604,3,242900
1962,4,259900
3890,3,573900
1100,3,249900
1458,3,464500
2526,3,469000
2200,3,475000
2637,3,299900
1839,2,349900
1000,1,169900
2040,4,314900
3137,3,579900
1811,4,285900
1437,3,249900
1239,3,229900
2132,4,345000
4215,4,549000
2162,4,287000
1664,2,368500

test_data.txt文件里面的数据如下：

2238,3,329900
2567,4,314000
1200,3,299000
852,2,179900
1852,4,299900
1203,3,239500

Logistic regression (Binary classification)

下图形象描述了什么是逻辑回归：
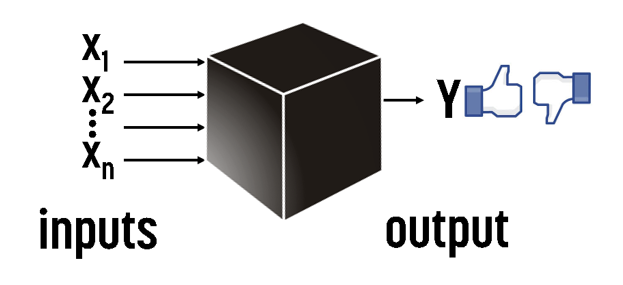
1.png-39.9kB
和线性回归不同，逻辑回归的结果只有两个值“true”或“false”。
逻辑回归的回归模型是sigmoid function, 也可以叫做logistic function：
1.png-28.9kB

下图说明了逻辑回归的目的：寻找θ
1.png-59kB

和线性回归一样，可以定义一个Cost Function，然后通过训练数据集调整参数θ使得Cost Function的值达到全局最优（最小值）
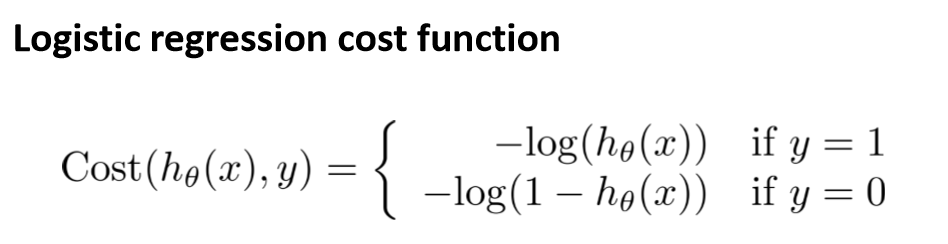
1.png-32.3kB

逻辑回归的梯度下降算法：
1.png-81.7kB

逻辑回归的一些优化:
1.png-36.8kB

逻辑回归代码实现：

    # coding: utf-8
    import matplotlib.pyplot as plt
    from numpy import *

    # 加载数据
    def load_data(filename):
        data = []; label = []
        with open(filename, 'r') as f:
            for line in f.readlines(): 
                line = line.strip().split()
                data.append([1.0, float(line[0]), float(line[1])])
                label.append(int(line[2]))
        return data, label

    # sigmoid 函数
    def sigmoid(z):
        return 1.0/(1+exp(-z))

    # 梯度下降
    def gradient_descent(dataMatIn, classLabels, alpha_value, interations_value):
        data = mat(dataMatIn)
        label = mat(classLabels).transpose()
        m,n = shape(data)
        alpha = alpha_value
        iterrations = interations_value
        weights = ones((n,1))
        for k in range(iterrations):
            z = data*weights
            h = sigmoid(z)
            weights = weights + alpha * data.transpose()* (label - h)
        return weights

    # 画图
    def plot_graph(weights, data_value, label_value):
        data = data_value
        label = label_value
        dataArr = array(data)
        n = shape(dataArr)[0]
        xcord1 = []; ycord1 = []
        xcord2 = []; ycord2 = []
        for i in range(n):
            if int(label[i])== 1:
                xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
            else:
                xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
        fig = plt.figure()
        ax = fig.add_subplot(111)
        ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
        ax.scatter(xcord2, ycord2, s=30, c='green')
        x = arange(-3.0, 3.0, 0.1)
        y = (-(float)(weights[0][0])-(float)(weights[1][0])*x)/(float)(weights[2][0])
        ax.plot(x,y)
        plt.xlabel('X1'); plt.ylabel('X2');
        plt.show()

    # 主函数
    def main():
        data, label = load_data('train_data.txt')
        alpha = 0.001
        iterrations = 500
        weights = gradient_descent(data, label, alpha, iterrations)
        print("The weights we found are:")
        print(weights)
        plot_graph(weights, data, label)

    if __name__=='__main__':
        main()

数据集
train_data.txt文件的数据如下：

-0.017612 14.053064 0
-1.395634 4.662541 1
-0.752157 6.538620 0
-1.322371 7.152853 0
0.423363 11.054677 0
0.406704 7.067335 1
0.667394 12.741452 0
-2.460150 6.866805 1
0.569411 9.548755 0
-0.026632 10.427743 0
0.850433 6.920334 1
1.347183 13.175500 0
1.176813 3.167020 1
-1.781871 9.097953 0
-0.566606 5.749003 1
0.931635 1.589505 1
-0.024205 6.151823 1
-0.036453 2.690988 1
-0.196949 0.444165 1
1.014459 5.754399 1
1.985298 3.230619 1
-1.693453 -0.557540 1
-0.576525 11.778922 0
-0.346811 -1.678730 1
-2.124484 2.672471 1
1.217916 9.597015 0
-0.733928 9.098687 0
-3.642001 -1.618087 1
0.315985 3.523953 1
1.416614 9.619232 0
-0.386323 3.989286 1
0.556921 8.294984 1
1.224863 11.587360 0
-1.347803 -2.406051 1
1.196604 4.951851 1
0.275221 9.543647 0
0.470575 9.332488 0
-1.889567 9.542662 0
-1.527893 12.150579 0
-1.185247 11.309318 0
-0.445678 3.297303 1
1.042222 6.105155 1
-0.618787 10.320986 0
1.152083 0.548467 1
0.828534 2.676045 1
-1.237728 10.549033 0
-0.683565 -2.166125 1
0.229456 5.921938 1
-0.959885 11.555336 0
0.492911 10.993324 0
0.184992 8.721488 0
-0.355715 10.325976 0
-0.397822 8.058397 0
0.824839 13.730343 0
1.507278 5.027866 1
0.099671 6.835839 1
-0.344008 10.717485 0
1.785928 7.718645 1
-0.918801 11.560217 0
-0.364009 4.747300 1
-0.841722 4.119083 1
0.490426 1.960539 1
-0.007194 9.075792 0
0.356107 12.447863 0
0.342578 12.281162 0
-0.810823 -1.466018 1
2.530777 6.476801 1
1.296683 11.607559 0
0.475487 12.040035 0
-0.783277 11.009725 0
0.074798 11.023650 0
-1.337472 0.468339 1
-0.102781 13.763651 0
-0.147324 2.874846 1
0.518389 9.887035 0
1.015399 7.571882 0
-1.658086 -0.027255 1
1.319944 2.171228 1
2.056216 5.019981 1
-0.851633 4.375691 1
以上数据来自数据链接

实验结果：
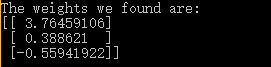
2.png-1.3kB
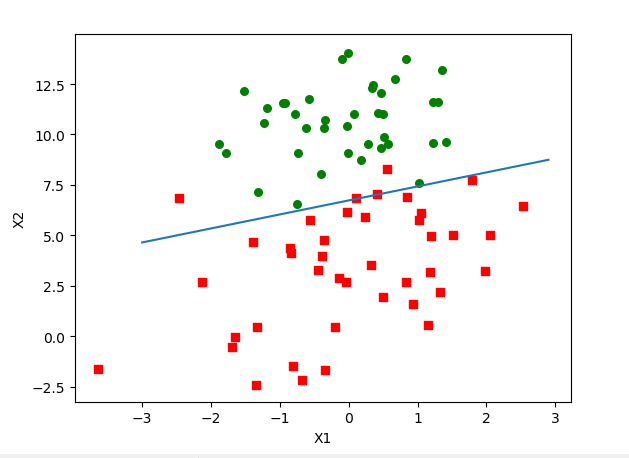
1.png-15.1kB

Softmax概念

PPT上面的的图貌似不好理解，下面有一张更容易理解的图：
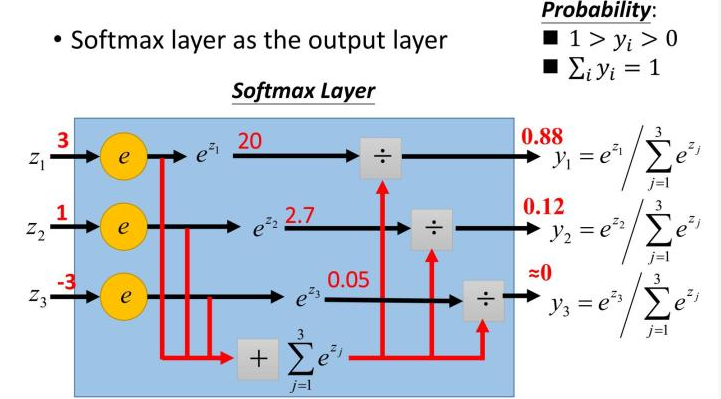
1.png-179.6kB
也就是说Softmax其实就是计算每一个变量的概率大小
Softmax代码实现：

import numpy as np
def softmax(x):
    return np.exp(x)/np.sum(np.exp(x),axis=0)

scores = [3.0, 1.0, -3.0]
print softmax(scores)

实验结果：
1.png-1.6kB

2 理解 CNN，并用简单 CNN 解决 mnist 数字识别问题

在编程实现MNIST数字识别之前首先来了解一些基础知识：
在Week1中我已经实现了一个比较简单的CNN识别MNIST数据集的CNN代码，这部分我将在Week1的基础上实现Deep CNN，进而得到更高的识别率。

Deep CNN结构介绍：

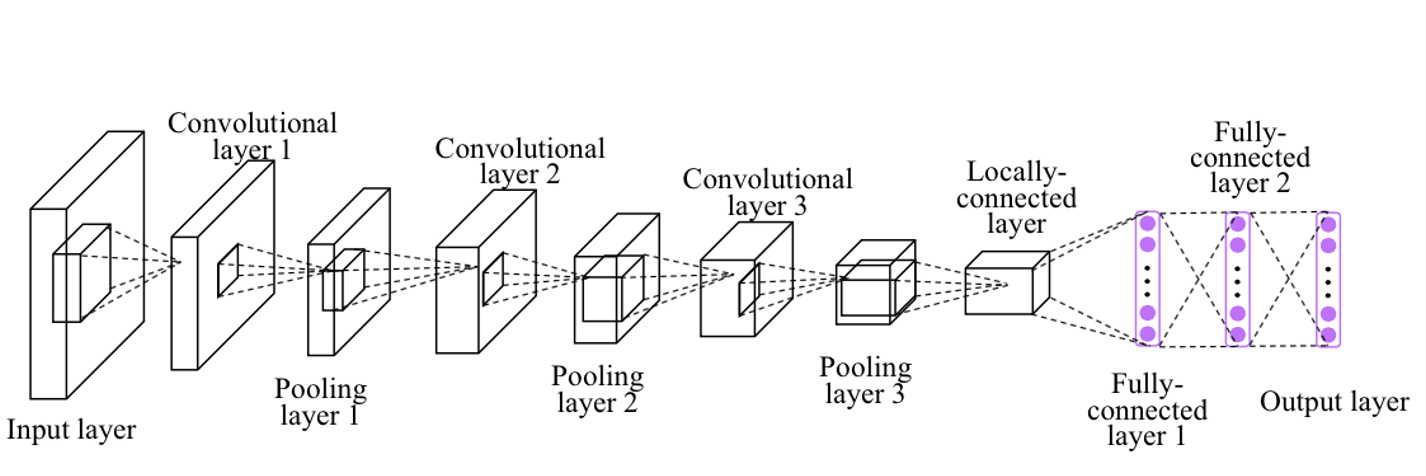
这个结构是DAY2的课件介绍的，分析一下PPT上面的源码：

这段代码对应图中的结构是Convolutional layer1和Pooling layer1

shape = [?, 28, 28, 1]的参数表示，？代表不确定有多少张图片同时输入，可能多张一起输入；两个28表示MNIST图片集的每一张图片是28*28像素点的；1代表每个像素点要么是0（黑色），要么是1（白色）；

W1的[3,3,1,32]参数的意义：两个3表示卷积核是3*3的；1表示输入图片的通道数，32表示输出的图片的通道数；也就是说这张图片和W1进行卷积操作之后得到的结果是：每个像素点的通道数是32。

3.png-4.1kB
这是一个常见的卷积操作，其中strides=[1,1,1,1]表示滑动步长为1，padding=‘SAME’表示填0操作,当我们要设置步长为2时，strides=[1,2,2,1];strides在官方定义中是一个一维具有四个元素的张量，前面一个1表示每次移动的batch个数是1，每次移动的通道数也是1，所以我们可以改的是中间两个数，中间两个数分别代表了水平滑动和垂直滑动步长值，于是就很好理解了。

tf.nn.relu 是激活操作，激活函数（activation function）将神经元计算的结果经过非线性表达映射到下一层。有关激活函数的理解请看链接:深度学习——激活函数Sigmoid/Tanh/ReLU

max_pool是池化层，可以理解为下采样操作
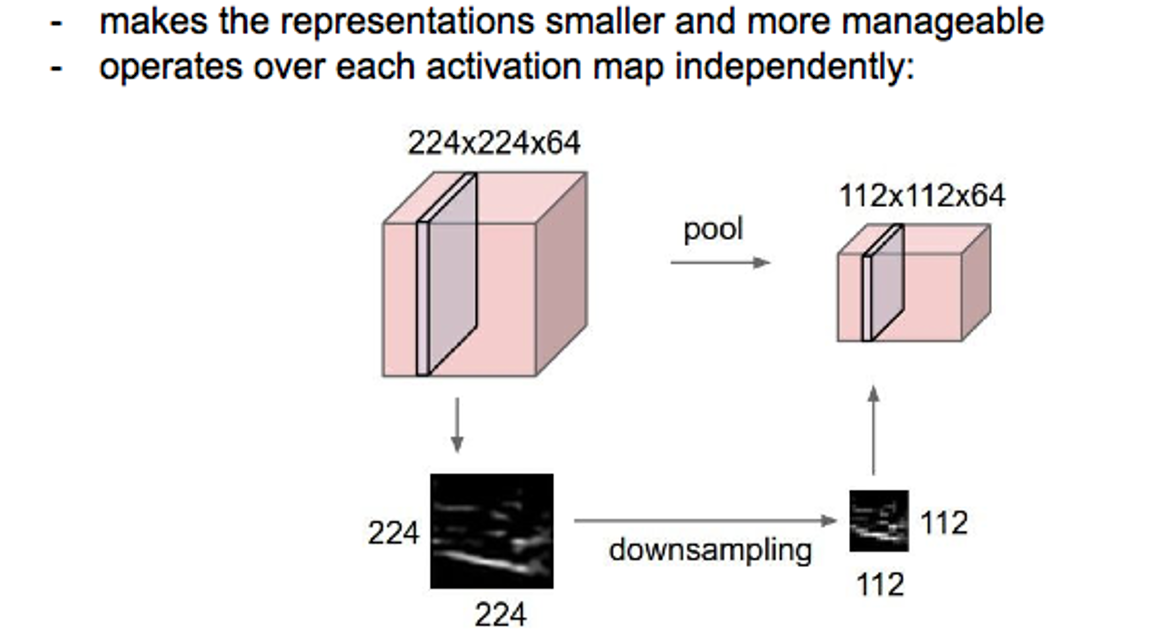
3.png-236kB
3.png-5.1kB
池化的模板的每次一个batch，一个channel，长为2，宽为2。

关于DropoutWeek1已经详细描述过。

Convolutional layer2和Pooling layer2、Convolutional layer3和Pooling layer3都与上面大同小异，在这里不再赘述。最终经过三个卷积层得到的图片结果是4*4*128的图片，长宽是4个像素，通道数是128。

Locally-connected layer的代码：
3.png-2.4kB
L3_flat是列数为128*4*4的二维矩阵
3.png-15.9kB
这部分的作用就是将输入的L3_falt经过矩阵相乘和Relu等操作变成[-1, 625]的输出矩阵

Fully-connected layer的代码：
3.png-12.4kB
这部分的作用就是将输入的[-1,625]矩阵经过矩阵相乘操作变成[-1,10]的输出矩阵，也就是说每一张图片对应0~9数字中的一个。

Depp CNN每一部分的功能：

关于CNN的介绍Week1已经详细介绍，这里简要复习概念
卷积层：简单理解就是卷积操作（数字图像处理）
池化层：就是将数据下采样，便于表示和管理
全连接层：将数据映射到指定空间便于分类
激活函数：神经元结果的非线性化处理
Dropout操作：避免overfitting

Tensorflow实现Deep CNN关键代码以及参数解释：

Tensorflow提供的接口最重要的是下面的两个接口：
3.png-85.8kB
以上图片来自CNN网络模型
可以参考上面的连接学习CNN的网络模型

Deep CNN实现代码以及解释：

# coding: utf-8
import tensorflow as tf
import random
from tensorflow.examples.tutorials.mnist import input_data
tf.set_random_seed(777)
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

alpha = 0.001
epochs = 15
batchs = 100 #这个参数表明我们每次迭代输入的图像是100张
keep_prob = tf.placeholder(tf.float32)

# 784代表28*28，也就是每一张图像的像素数目，None代表不确定一共要输入多少张图像
X = tf.placeholder(tf.float32, [None, 784])
# 这里是将X变成28*28 每个像素点只有黑（0）、白（1）两种值的图像
X_img = tf.reshape(X, [-1, 28, 28, 1])
# 存放输出结果，每一行代表每一张图片最终的结果对应于0~9数字中的哪一个
Y = tf.placeholder(tf.float32, [None, 10])


# L1 ImgIn shape=(?, 28, 28, 1) ？代表不确定一共要输出多少张图像
# W1是3*3卷积核，输入通道数为1，输出通道数为32，也就是说卷积操作之后得到的图像的每一个像素点的通道数为32
W1 = tf.Variable(tf.random_normal([3, 3, 1, 32], stddev=0.01))
# 卷积操作，strides的第一个和最后一个参数表明每次移动的batch个数是1，每次移动的通道数也是1
# 中间两个参数分别代表了水平滑动和垂直滑动步长值， padding=‘SAME’表示卷积得到的图像大小和输入图像一样
L1 = tf.nn.conv2d(X_img, W1, strides=[1, 1, 1, 1], padding='SAME')
# 激活函数
L1 = tf.nn.relu(L1)
# 池化层，可以理解为下采样操作。ksize中间两个参数表明模板的大小是2*2
# strides中间两个参数表明水平滑动和垂直滑动步长值都为2，也就是说最终得到的图像大小是原图像的一半
L1 = tf.nn.max_pool(L1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
# dropout操作，为了避免overfitting
L1 = tf.nn.dropout(L1, keep_prob=keep_prob)

# L2 ImgIn shape=(?, 14, 14, 32)
# L2的过程和L1的类似，这里不再赘述
# 注意的是L2最终的输出结果是(?,7,7,64)
# 因为W2的后两个参数分别是32、64，代表输入图像的通道数为32，经过卷积操作输出图像的通道数为64
# 此外池化层的模板大小以及步长依旧没有改变，意味着输出图像是输入图像长宽的一半
W2 = tf.Variable(tf.random_normal([3, 3, 32, 64], stddev=0.01))
L2 = tf.nn.conv2d(L1, W2, strides=[1, 1, 1, 1], padding='SAME')
L2 = tf.nn.relu(L2)
L2 = tf.nn.max_pool(L2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
L2 = tf.nn.dropout(L2, keep_prob=keep_prob)

# L3 ImgIn shape=(?, 7, 7, 64)
# L3的过程和L1的类似，这里不再赘述
# 注意的是L3最终的输出结果是(?,4,4,128)
# 因为W3的后两个参数分别是64、128，代表输入图像的通道数为64，经过卷积操作输出图像的通道数为128
# 此外池化层的模板大小以及步长依旧没有改变，意味着输出图像是输入图像长宽的一半，由于padding=‘SAME’补0，这样池化后的结果为4*4
W3 = tf.Variable(tf.random_normal([3, 3, 64, 128], stddev=0.01))
L3 = tf.nn.conv2d(L2, W3, strides=[1, 1, 1, 1], padding='SAME')
L3 = tf.nn.relu(L3)
L3 = tf.nn.max_pool(L3, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
L3 = tf.nn.dropout(L3, keep_prob=keep_prob)
# 这是比较关键的一步，这一步的作用就是将L3处理后的结果变成列数为128*4*4的二维矩阵，便于后面的操作
L3_flat = tf.reshape(L3, [-1, 128 * 4 * 4])

# L4 FC 4x4x128 inputs -> 625 outputs
# 这部分的代码比较容易理解，就是将输入的每一行（代表一个图像的数据）从高维数据映射到625维的数据
# 经过矩阵相乘、先行相加、到最后Relu非线性化激活
W4 = tf.get_variable("W4", shape=[128 * 4 * 4, 625], initializer=tf.contrib.layers.xavier_initializer())
b4 = tf.Variable(tf.random_normal([625]))
L4 = tf.nn.relu(tf.matmul(L3_flat, W4) + b4)
L4 = tf.nn.dropout(L4, keep_prob=keep_prob)

# L5 Final FC 625 inputs -> 10 outputs
# 这部分代码就是将每一行625的数据映射到10维数据，正好对应于0~9
W5 = tf.get_variable("W5", shape=[625, 10], initializer=tf.contrib.layers.xavier_initializer())
b5 = tf.Variable(tf.random_normal([10]))
logits = tf.matmul(L4, W5) + b5

# 定义损失函数和优化器，我们做的工作的最终目的就是找到一组参数使得损失函数的值达到最小（全局最优）
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=Y))
optimizer = tf.train.AdamOptimizer(learning_rate=alpha).minimize(cost)

# 开始利用tensorflow来run我们已经建立好的graph
sess = tf.Session()
sess.run(tf.global_variables_initializer())

# 训练开始
print('训练开始：')
for epoch in range(epochs):
    avg_cost = 0
    total_batch = int(mnist.train.num_examples / batchs)

    for i in range(total_batch):
        batch_xs, batch_ys = mnist.train.next_batch(batchs)
        feed_dict = {X: batch_xs, Y: batch_ys, keep_prob: 0.7}
        c, _ = sess.run([cost, optimizer], feed_dict=feed_dict)
        avg_cost += c / total_batch
        print('  Batch:', '%d' % (i + 1), 'cost =', '{:.9f}'.format(avg_cost))

    print('Epoch:', '%d' % (epoch + 1), 'cost =', '{:.9f}'.format(avg_cost))

print('训练结束')

correct_prediction = tf.equal(tf.argmax(logits, 1), tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
print('识别精度为:', sess.run(accuracy, feed_dict={X: mnist.test.images, Y: mnist.test.labels, keep_prob: 1}))

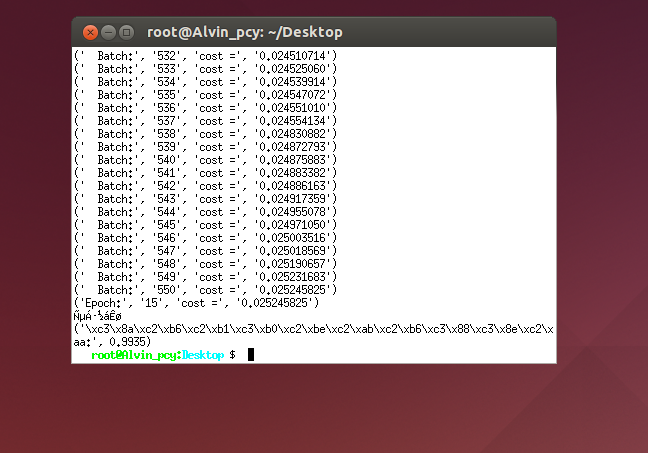
实验结果：

由于中文字符的原因显示出了乱码，但是仍然可以看到识别精度高达99.35%
3.png-133.4kB

3 了解 LeNet

LeNet网络结构：

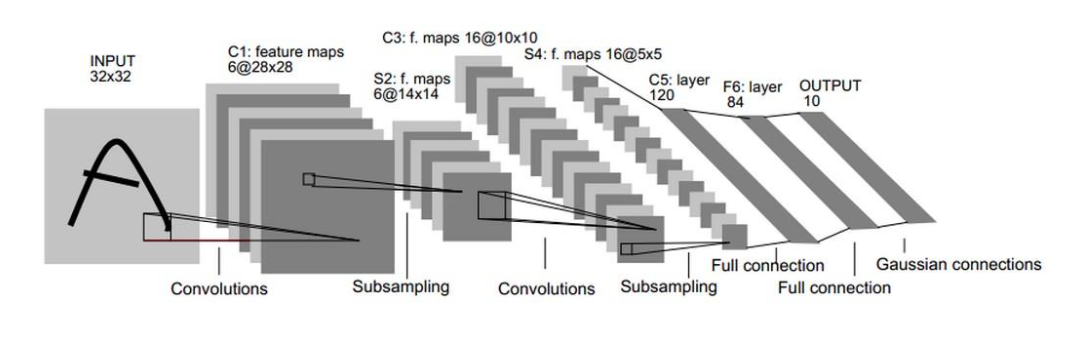
1.png-161.1kB
LeNet-5一共有7层：
第一层：卷积层
第一层卷积层的输入为原始的图像，原始图像的尺寸为32×32×1。卷积核的size为5×5，深度为6，不使用全0补充，步长为1；输出的featuremap为28*28；可训练参数为5*5*6个
第二层：池化层
进行下采样操作，输入图像为28*28*6，输出为14*14*6；
第三层：卷积层
输入的数据图像size为14*14*6，卷积核的size为5×5，深度为16，不使用全0补充，步长为1；输出的图像数据size为10*10*16；本层参数有5*5*6*16个
第四层：池化层
进行下采样操作，输入图像为10*10*16，输出为5*5*16；
第五层：全连接层
本层输入为5*5*16矩阵，将其拉直为一个长度为5*5*16的向量，即将一个三维矩阵拉直到一维空间以向量的形式表示，这样才可以进入全连接层进行训练。本层的输出节点个数为120，所以总共有5*5*16*120+120=48120个参数。
第六层：全连接层
本层的输入节点个数为120个，输出节点个数为84个，总共有120*84+84=10164个参数。
第七层：全连接层
本层的输入节点个数为84个，输出节点个数为10个，总共有84*10+10=850个参数。

代码实现：

代码参考了《Tensorflow实战Google深度学习框架》P150-P154
我发现书上的参数和LeNet论文给的参数不一样，所以采用了书上的参数完成LeNet网络

# coding: utf-8
import tensorflow as tf
import random
from tensorflow.examples.tutorials.mnist import input_data
tf.set_random_seed(777)
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

alpha = 0.001
epochs = 15
batchs = 100 #这个参数表明我们每次迭代输入的图像是100张
keep_prob = tf.placeholder(tf.float32)

# 784代表28*28，也就是每一张图像的像素数目，None代表不确定一共要输入多少张图像
X = tf.placeholder(tf.float32, [None, 784])
# 这里是将X变成28*28 每个像素点只有黑（0）、白（1）两种值的图像
X_img = tf.reshape(X, [-1, 28, 28, 1])
# 存放输出结果，每一行代表每一张图片最终的结果对应于0~9数字中的哪一个
Y = tf.placeholder(tf.float32, [None, 10])


# L1 ImgIn shape=(?, 28, 28, 1) ？代表不确定一共要输出多少张图像
# W1是5*5卷积核，输入通道数为1，输出通道数为32，也就是说卷积操作之后得到的图像的每一个像素点的通道数为32
W1 = tf.Variable(tf.random_normal([5, 5, 1, 32], stddev=0.01))
# 卷积操作，strides的第一个和最后一个参数表明每次移动的batch个数是1，每次移动的通道数也是1
# 中间两个参数分别代表了水平滑动和垂直滑动步长值， padding=‘SAME’表示卷积得到的图像大小和输入图像一样
L1 = tf.nn.conv2d(X_img, W1, strides=[1, 1, 1, 1], padding='SAME')
# 激活函数
L1 = tf.nn.relu(L1)
# 池化层，可以理解为下采样操作。ksize中间两个参数表明模板的大小是2*2
# strides中间两个参数表明水平滑动和垂直滑动步长值都为2，也就是说最终得到的图像大小是原图像的一半
L1 = tf.nn.max_pool(L1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
# dropout操作，为了避免overfitting
L1 = tf.nn.dropout(L1, keep_prob=keep_prob)

# L2 ImgIn shape=(?, 14, 14, 32)
# L2的过程和L1的类似，这里不再赘述
# 注意的是L2最终的输出结果是(?,7,7,64)
# 因为W2的后两个参数分别是32、64，代表输入图像的通道数为32，经过卷积操作输出图像的通道数为64
# 此外池化层的模板大小以及步长依旧没有改变，意味着输出图像是输入图像长宽的一半
W2 = tf.Variable(tf.random_normal([5, 5, 32, 64], stddev=0.01))
L2 = tf.nn.conv2d(L1, W2, strides=[1, 1, 1, 1], padding='SAME')
L2 = tf.nn.relu(L2)
L2 = tf.nn.max_pool(L2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
L2 = tf.nn.dropout(L2, keep_prob=keep_prob)

# 输入[-1, 7*7*64]的矩阵，输出[-1, 512]的矩阵
W_fc1 = tf.Variable(tf.truncated_normal([7*7*64, 512], stddev=0.1))
b_fc1 = tf.Variable(tf.constant(0.1, shape = [512])) 
h_pool2_flat = tf.reshape(L2,[-1,7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat,W_fc1) + b_fc1)
h_fc1 = tf.nn.dropout(h_fc1, keep_prob=keep_prob)

# 输入[-1, 512]的矩阵，输出[-1, 10]的矩阵
W_fc2 = tf.Variable(tf.truncated_normal([512,10], stddev=0.1))
b_fc2 = tf.Variable(tf.constant(0.1, shape = [10]))
logits = tf.nn.softmax(tf.matmul(h_fc1,W_fc2) + b_fc2)

# 定义损失函数和优化器，我们做的工作的最终目的就是找到一组参数使得损失函数的值达到最小（全局最优）
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=Y))
optimizer = tf.train.AdamOptimizer(learning_rate=alpha).minimize(cost)

# 开始利用tensorflow来run我们已经建立好的graph
sess = tf.Session()
sess.run(tf.global_variables_initializer())

# 训练开始
print('训练开始：')
for epoch in range(epochs):
    avg_cost = 0
    total_batch = int(mnist.train.num_examples / batchs)

    for i in range(total_batch):
        batch_xs, batch_ys = mnist.train.next_batch(batchs)
        feed_dict = {X: batch_xs, Y: batch_ys, keep_prob: 0.7}
        c, _ = sess.run([cost, optimizer], feed_dict=feed_dict)
        avg_cost += c / total_batch
        print('  Batch:', '%d' % (i + 1), 'cost =', '{:.9f}'.format(avg_cost))

    print('Epoch:', '%d' % (epoch + 1), 'cost =', '{:.9f}'.format(avg_cost))

print('训练结束')

correct_prediction = tf.equal(tf.argmax(logits, 1), tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
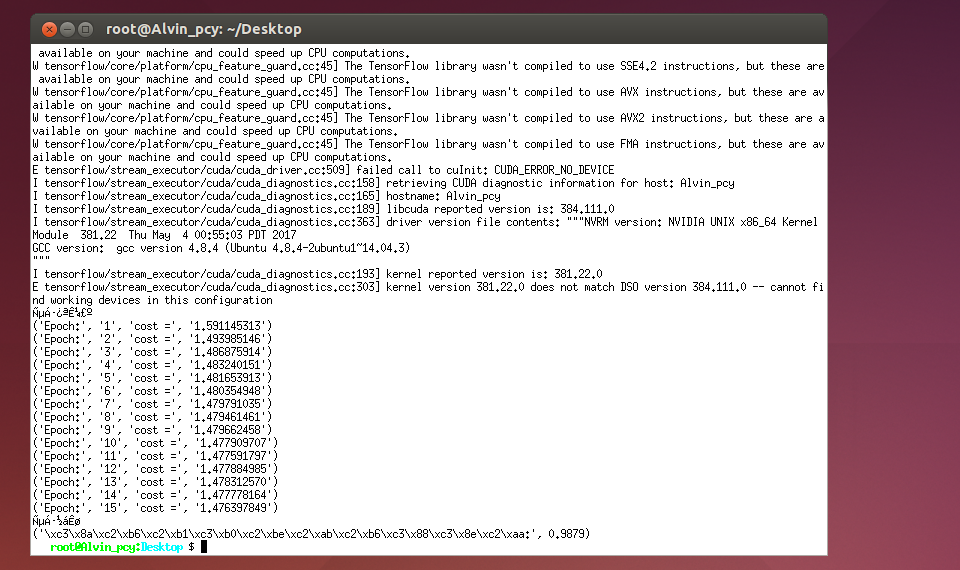
print('识别精度为:', sess.run(accuracy, feed_dict={X: mnist.test.images, Y: mnist.test.labels, keep_prob: 1}))

实验结果：

由于中文字符的原因显示出了乱码，但是仍然可以看到识别精度达98.79%
1.png-156.8kB

Alvin's Tech Blog

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
TensorFlow+深度学习笔记2

TensorFlow+深度学习笔记2标签（空格分隔）：TensorFlow+深度学习笔记本周掌握的知识：深度学习基本概念理解：Linear regression、Logistic regression、Softmax。并使用python完成对应代码实现；在课件的指导下，参考示例实现了Deep CNN, 最终的识别率达到99.35%；了解了LeNet，参考《Tensorfl...
复制链接

扫一扫