深度学习优化函数详解

深度学习优化函数详解系列目录
深度学习优化函数详解（0）– 线性回归问题
深度学习优化函数详解（1）– Gradient Descent 梯度下降法
深度学习优化函数详解（2）– SGD 随机梯度下降

深度学习优化函数详解（0）-- 线性回归问题

序

在做一些深度学习的算法的时候，都会用到优化函数，在各种成熟的框架中，基本就是一行代码的事，甚至连默认参数都给你设置好了，基本不用动什么东西，最后也会有比较好的优化结果。但是对于优化函数这么核心，这么基本的东西总是模棱两可实在不应该。于是想自己把一些常用的优化函数从原理上搞清楚，所以才有了这个系列的文章。每一篇文章都有配套的Python代码，文末会给出地址。

线性回归问题（Linear Regression）

假设我们有一组数据，是一些房子的面积和价格。如下

面积	30	35	37	59	70	76	88	100
价格	1100	1423	1377	1800	2304	2588	3495	4839

用这些数据我们可以在坐标系中绘制出一系列散点

我们所想要解决的问题，就是给出任意的一个面积，预测对应的房价。 所以这是一个预测问题。也就是回归问题。
这里我们用最简单的线形模型来做房价预测。那么这个问题也可以称之为线性回归问题。

线形模型简单来说就是直角坐标系中的一根线，用

y=ax+b

表示。这里 a 和 b 就是我们要优化的参数。换句话说，我们要通过接下来写的一套算法，找到最优的 a 和 b 。很明显，人眼来看上面的图，直接可以画出一条斜线，但对于机器来说，这个事就有点困难了。假设我们先给定一组参数 a=1,b=0 ,画一条线看看

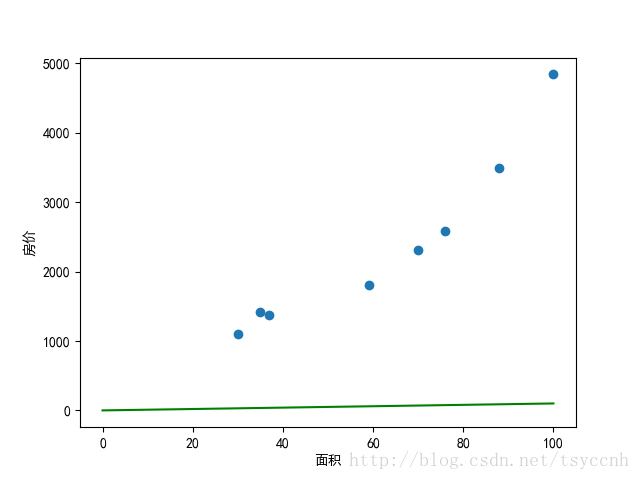
可以看出，参数 a 并未提供太大的斜率，这是由于横坐标和纵坐标尺度差距太大所造成的，在后期的训练中，数据在各个维度上尺度差异太大很容易造成训练速度过慢。所以一般来说，在训练之前，我们首先会对数据做归一化处理，统一归到 [0,1] 之间，上公式：

xnew=x−xminxmax−xmin

这样就得到归一化之后的数据

面积(x)	0.0	0.0714	0.1	0.4143	0.5714	0.6571	0.8286	1.0
价格(y)	0.0	0.0864	0.0741	0.1872	0.3220	0.3980	0.6405	1.0

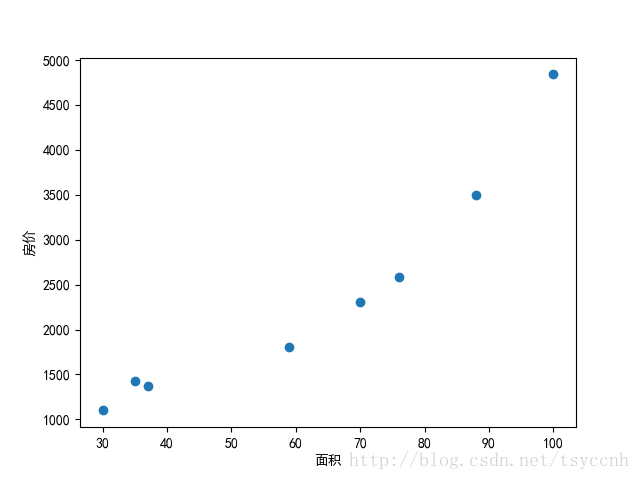
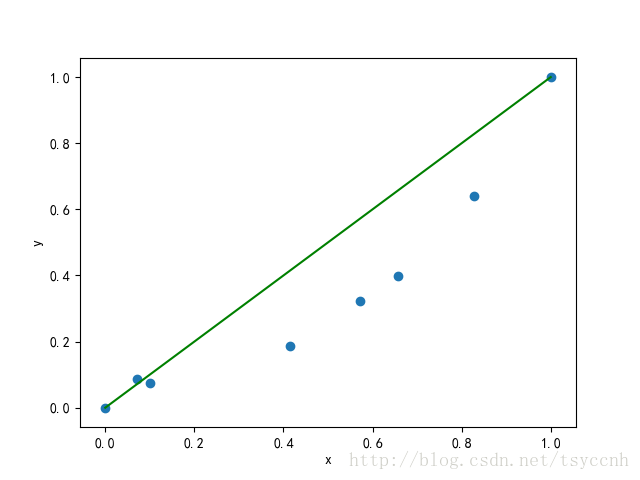
再画一遍上面的图。

再对数据做过预处理之后，我们现在就来评判 y=x(a=1,b=0) 这条线多大程度上完成了预测。显然的，我们会用到我们的训练数据 代入到模型 y=x 中，看看和实际结果差多少。通过模型得到的结果我们称之为预测值 yp

面积(x)	0.0	0.0714	0.1	0.4143	0.5714	0.6571	0.8286	1.0
价格(y)	0.0	0.0864	0.0741	0.1872	0.3220	0.3980	0.6405	1.0
预测值( yp )	0.0	0.0714	0.1	0.4143	0.5714	0.6571	0.8286	1.0
差值( yp−y )	0	-0.015	0.0259	0.2271	0.2494	0.2592	0.1880	0

通过差值可以很明显的看出预测和实际真值有一定的差距，那么如何定量描述这种差距呢？通常我们会用差值的平方和 来表示，如下

差值的平方和 (yp−y)2	0	0.000225	0.00067081	0.05157441	0.06220036	0.06718464	0.035344	0

接着把每一个平方和的值做一个累加，得到一个值0.2172。我们一共有8组数据，再把这个数除以8。然后再除以2，就得到了一个我们称之为loss的数值0.01357,写成公式就是下面这样：

loss=12m∑i=1m(yp,i−yi)2

除以2是为了后面求梯度的时候方便，除以m是做一个平均的量化。

这种求loss的方法称之为Mean Squared Error (MSE), 即均方差。

接下来的目标很明确，就是

如何不断的调整参数 a,b 来使loss越来越小，最终令预测尽可能接近真实值。

从这一点出发，很多人做了很多不同的工作，我们将这些方法统称为优化函数

后面的文章将一一解读各种常用的优化函数

本文代码地址：https://github.com/tsycnh/mlbasic/blob/master/p0.py

深度学习优化函数详解（1）-- Gradient Descent 梯度下降法

上一篇讲到了最基本的线性回归问题，最终就是如何优化参数 a,b 寻找最小的loss

loss=12m∑i=1m(yp,i−yi)2

显然loss函数是一个二次函数，问题就转化成了如何求二次函数的最小值。我们再举一个更简单的例子，假设我们要优化的函数是 y=x2 ，初始条件我们选择了 x0=2,y0=4 ,画在图上如下：

图中红色的点就是我们的初始点，很显然，我们想要找的最终最优点是绿色的点 (0,0) 。
接下来我们需要对目标函数求微分

dydx=2x

这就是所谓的 梯度，当 x=2 的时候，可以求得该点的梯度为4，翻译成人话就是当前这一点的’倾斜程度’是4。下面举几个例子

x	-2	-1	0	1	2
y	4	1	0	1	4
梯度	-4	-2	0	1	4

和上面的图一对应就很明显了，梯度的绝对值越大，数据点所在的地方就越陡。数字为正数时，越大，表示越向右上方陡峭，反之亦然。好了，懂了什么是梯度，下面我们就来聊聊梯度下降是个什么玩意。现在我们先假设我们自己就是一个球，呆在图中的红点处，我们的目标是到绿点处，该怎么走呢？很简单，顺着坡 向下走就行了。现在球在 (2,4) 点处，这一点的倾斜程度是4，向右上方陡峭。接下来要做的就是向山下走，那么每一次走多远 呢？先小心一点，按当前倾斜程度的1%向下走。也就是 xnew=x0−0.01∗4 , xnew=1.96 再算一下 y 值等于多少 ynew=3.8416<4 。小球成功的往下滚了一点，这样一直滚下去，最终就会滚到绿色的点，如下图

红色的曲线表示了小球的滚动路线

这 就是梯度下降法

转换成数学语言就是在每一次迭代按照一定的学习率 α 沿梯度的反方向更新参数，直至收敛，公式

θt+1=θt−αdfdθ

接下来我们回到房价预测问题上。

yp,i=axi+b

loss=12m∑i=1m(yp,i−yi)2

将上面两个方程合并, 并把1/2放到右边方程

loss=1m∑i=1m12(axi+b−yi)2

一共有m项累加，我们单拿出来一项来分析。

lossi=12(axi+b−yi)2

要优化的参数有两个，分别是a和b，我们分别对他们求微分，也就是 偏微分

∂lossi∂a=(axi+b−yi)xi

∂lossi∂b=(axi+b−yi)

这里我们看到了loss函数为什么要在前面加一个1/2，目的就是在求偏微分的时候，可以把平方项中和掉，方便后面的计算。
自然地我们将每一个 ∂lossi∂a 和 ∂lossi∂b 累加起来得到

∂loss∂a=1m∑i=1m∂lossi∂a

∂loss∂b=1m∑i=1m∂lossi∂b

∂loss∂a 记为 ∇a ∂loss∂b 记为 ∇b ,分别表示loss在a、b方向的梯度, 更新参数的方法如下

anew=a−α∇a

bnew=b−α∇b

实验

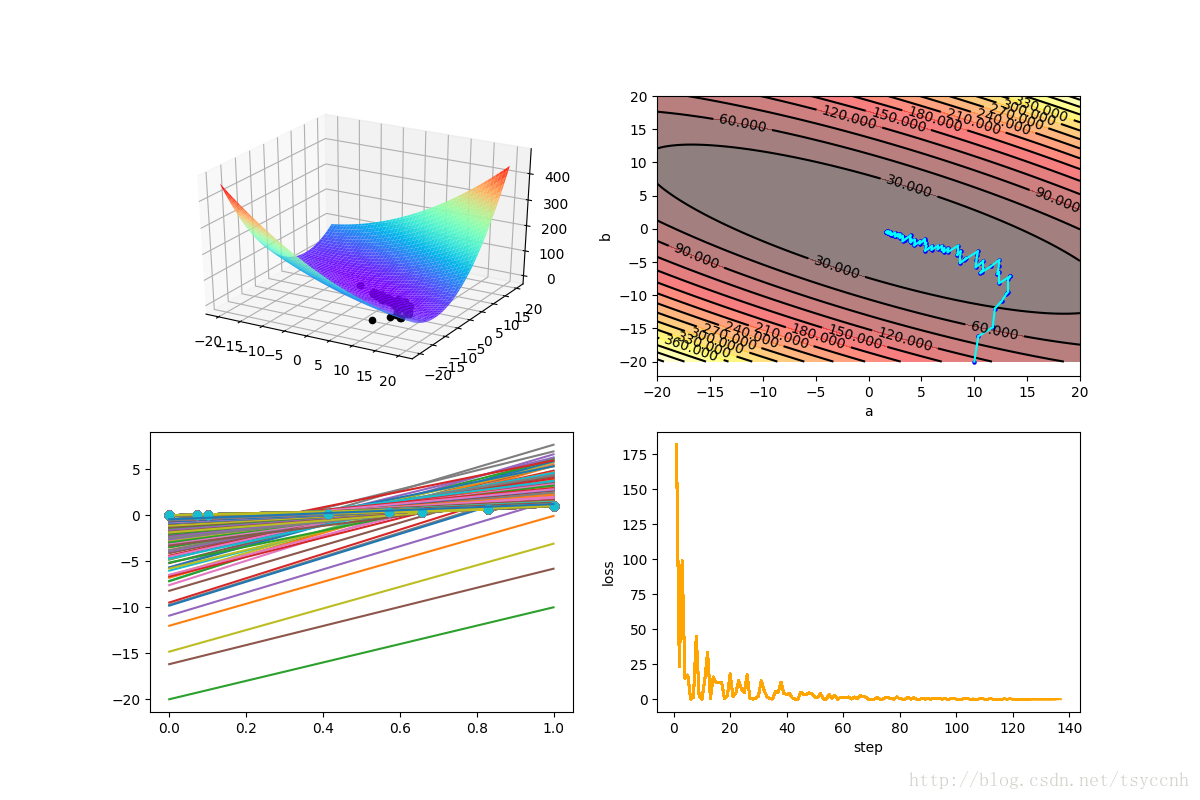
写了这么多公式，是时候直观的看一看梯度下降法是怎么一回事了。下面将绘制四幅图，分别是
1. 在a,b的一定的取值范围内，计算所有的loss，绘制出分布图
2. 将这张分布图拍扁，画出等高线图
3. 绘制原始的数据折线以及依据a,b绘制预测直线
4. 绘制在训练过程中loss的变化
如下

我们看到图1和之前二次函数的那个例子很像，只不过是在三维空间内的一个曲面，初始的参数选择 a=15,b=10 ，可以看到图1上曲面右侧有一个浅浅的点，就是初始值了。图二是等高线图，俯视更加明显，等高线图主要是为了之后训练的过程中可视化更清晰。图三上方的绿线是根据选择的初始值绘制的，下方是真实的实验数据，可以看出差距很远，需要优化的步骤还很多。将学习率 α 设置为0.01, 经过200次迭代，结果如下图

图一和图二都可以很直观的看到loss的减小。图三也从模型上给出了最终逼近的过程。图四可以看出下降还是很快的。
值得注意的是，不同的学习率对算法的收敛速度影响很大，下图是 α=0.15 的结果

基本在前10次迭代就快速收敛。
但是如果学习率设置的太大的话，很容易造成发散。说白了就是步子迈的太大了，一步迈到对面更高的山坡上去了，结果越迈越高，最后就不知道跑到哪里去了，如下图 ( α=0.3 )

每个图请注意看坐标轴的尺度，都大的不行，一开始的画的曲面和和等高线图都变得十分小，而这也只是迭代了5步而已。

所以机器学习里面，参数的选择是个技术活，往往同一个模型，两个人调参，结果却大相径庭。

本文的源码在此 https://github.com/tsycnh/mlbasic/blob/master/p1%20gradient%20descent.py

深度学习优化函数详解（2）-- SGD 随机梯度下降

上文讲到的梯度下降法每进行一次 迭代 都需要将所有的样本进行计算，当样本量十分大的时候，会非常消耗计算资源，收敛速度会很慢。尤其如果像ImageNet那样规模的数据，几乎是不可能完成的。同时由于每次计算都考虑了所有的训练数据，也容易造成过拟合。在某种程度上考虑的太多也会丧失 随机性 。于是有人提出，既然如此，那可不可以每一次迭代只计算一个样本的loss呢？然后再逐渐遍历所有的样本，完成一轮（epoch）的计算。答案是可以的，虽然每次依据单个样本会产生较大的波动，但是从整体上来看，最终还是可以成功收敛。由于计算量大大减少，计算速度也可以极大地提升。这种逐个样本进行loss计算进行迭代的方法，称之为 Stochasitc Gradient Descent 简称SGD。

注：目前人们提到的SGD一般指 mini-batch Gradient Descent，是经典SGD的一个升级。后面的文章会讲到。

公式推导

我们再来回顾一下参数更新公式。每一次迭代按照一定的学习率 α 沿梯度的反方向更新参数，直至收敛

θt+1=θt−αdfdθ

接下来我们回到房价预测问题上。线形模型：

yp,i=axi+b

这是经典梯度下降方法求loss，每一个样本都要经过计算：

loss=12m∑i=1m(yp,i−yi)2

这是SGD梯度下降方法：

loss=12(yp,i−yi)2

要优化的参数有两个，分别是a和b，我们分别对他们求微分，也就是偏微分

∂loss∂a=(axi+b−yi)xi

∂loss∂b=(axi+b−yi)

∂loss∂a 记为 ∇a ∂loss∂b 记为 ∇b ,分别表示loss在a、b方向的梯度, 更新参数的方法如下

anew=a−α∇a

bnew=b−α∇b

实验

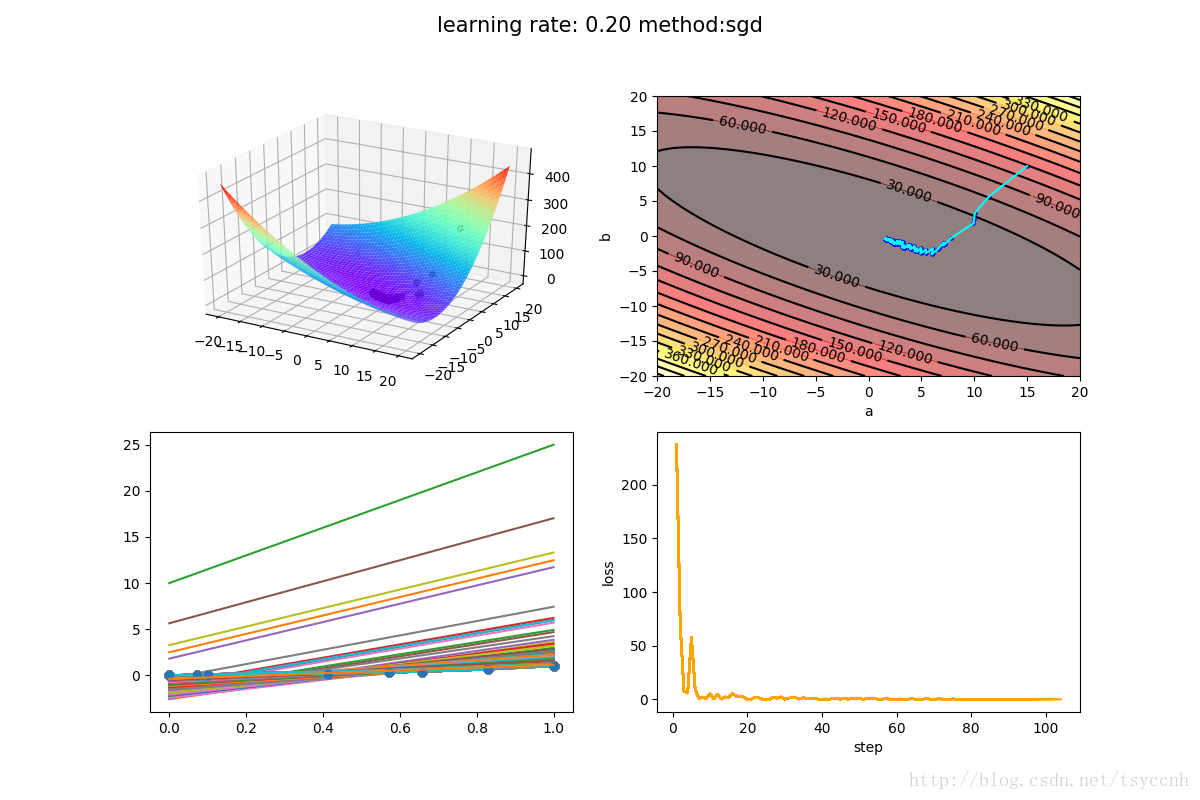
直接看图

关于图中四个子图的意义，请参看 深度学习优化函数详解（1）– Gradient Descent 梯度下降法

等高线图和loss图都很明显的表现了SGD的特点。总体上收敛，局部有一些震荡。

由于加入了随机的成分，有的时候可能算法有一点点走偏，但好处就是对于一些局部极小点可以从坑中跳出，奔向理想中的全局最优。

实验代码下载：https://github.com/tsycnh/mlbasic/blob/master/p2%20origin%20SGD.py

深度学习优化函数详解（3）-- mini-batch SGD 小批量随机梯度下降

本文延续该系列的上一篇 深度学习优化函数详解（2）– SGD 随机梯度下降

上一篇我们说到了SGD随机梯度下降法对经典的梯度下降法有了极大速度的提升。但有一个问题就是由于过于自由 导致训练的loss波动很大。那么如何可以兼顾经典GD的稳定下降同时又保有SGD的随机特性呢？于是小批量梯度下降法, mini-batch gradient descent 便被提了出来。其主要思想就是每次只拿总训练集的一小部分来训练，比如一共有5000个样本，每次拿100个样本来计算loss，更新参数。50次后完成整个样本集的训练，为一轮（epoch）。由于每次更新用了多个样本来计算loss，就使得loss的计算和参数的更新更加具有代表性。不像原始SGD很容易被某一个样本给带偏 。loss的下降更加稳定，同时小批量的计算，也减少了计算资源的占用。

公式推导

我们再来回顾一下参数更新公式。每一次迭代按照一定的学习率 α 沿梯度的反方向更新参数，直至收敛

θt+1=θt−αdfdθ

接下来我们回到房价预测问题上。线形模型：

yp,i=axi+b

这是经典梯度下降方法求loss，每一个样本都要经过计算：

loss=12m∑i=1m(yp,i−yi)2

这是SGD梯度下降方法：

loss=12(yp,i−yi)2

这是mini-batch 梯度下降法, k表示每一个batch的总样本数：

lossbatch=12k∑i=1k(yp,i−yi)2

要优化的参数有两个，分别是a和b，我们分别对他们求微分，也就是偏微分, 再求和的均值

∂lossbatch∂a=1k∑i=1k(axi+b−yi)xi

∂lossbatch∂b=1k∑i=1k(axi+b−yi)

∂lossbatch∂a 记为 ∇a ∂lossbatch∂b 记为 ∇b ,分别表示loss在a、b方向的梯度, 更新参数的方法如下

anew=a−α∇a

bnew=b−α∇b

实验

小技巧：在每一个epoch计算完所有的样本后，计算下一代样本的时候，可以选择打乱所有样本顺序。

下面是SGD方法的训练结果

下面是 mini-batch SGD方法的训练结果

由于我的训练样本比较少，所以选择了比较大的学习率来体现效果。mini-batch SGD中，每次选择3个样本作为一个batch进行训练。容易看出，波动的减小还是比较明显。同时手链的速度也是大大加快，几乎一步就走到了合适的参数范围。

由于mini-batch SGD 比 SGD 效果好很多，所以人们一般说SGD都指的是 mini-batch gradient descent. 大家不要和原始的SGD混淆。现在基本所有的大规模深度学习训练都是分为小batch进行训练的。

本文全部代码实现：https://github.com/tsycnh/mlbasic/blob/master/p3%20minibatch%20SGD.py

深度学习优化函数详解（4）-- momentum 动量法

如果把梯度下降法想象成一个小球从山坡到山谷的过程，那么前面几篇文章的小球是这样移动的：从A点开始，计算当前A点的坡度，沿着坡度最大的方向走一段路，停下到B。在B点再看一看周围坡度最大的地方，沿着这个坡度方向走一段路，再停下。确切的来说，这并不像一个球，更像是一个正在下山的盲人，每走一步都要停下来，用拐杖来来探探四周的路，再走一步停下来，周而复始，直到走到山谷。而一个真正的小球要比这聪明多了，从A点滚动到B点的时候，小球带有一定的初速度，在当前初速度下继续加速下降，小球会越滚越快，更快的奔向谷底。momentum 动量法就是模拟这一过程来加速神经网络的优化的。

后文的公式推导不加特别说明都是基于 mini-batch SGD 的，请注意。

公式推导

更多实验数据背景及模型定义请参看该系列的前几篇文章。

上图直观的解释了动量法的全部内容。
A为起始点，首先计算A点的梯度 ∇a ,然后下降到B点，

θnew=θ−α∇a

θ 为参数 α 为学习率。
到了B点需要加上A点的梯度，这里梯度需要有一个衰减值 γ ,推荐取0.9。这样的做法可以让早期的梯度对当前梯度的影响越来越小，如果没有衰减值，模型往往会震荡难以收敛，甚至发散。所以B点的参数更新公式是这样的：

vt=γvt−1+α∇b

θnew=θ−vt

其中 vt−1 表示之前所有步骤所累积的动量和。
这样一步一步下去，带着初速度的小球就会极速的奔向谷底。

实验

由于样本数量较少，动量的实验未使用SGD，每一次更新loss使用全部数据

学习率 α=0.01 ，衰减率 γ=0.9
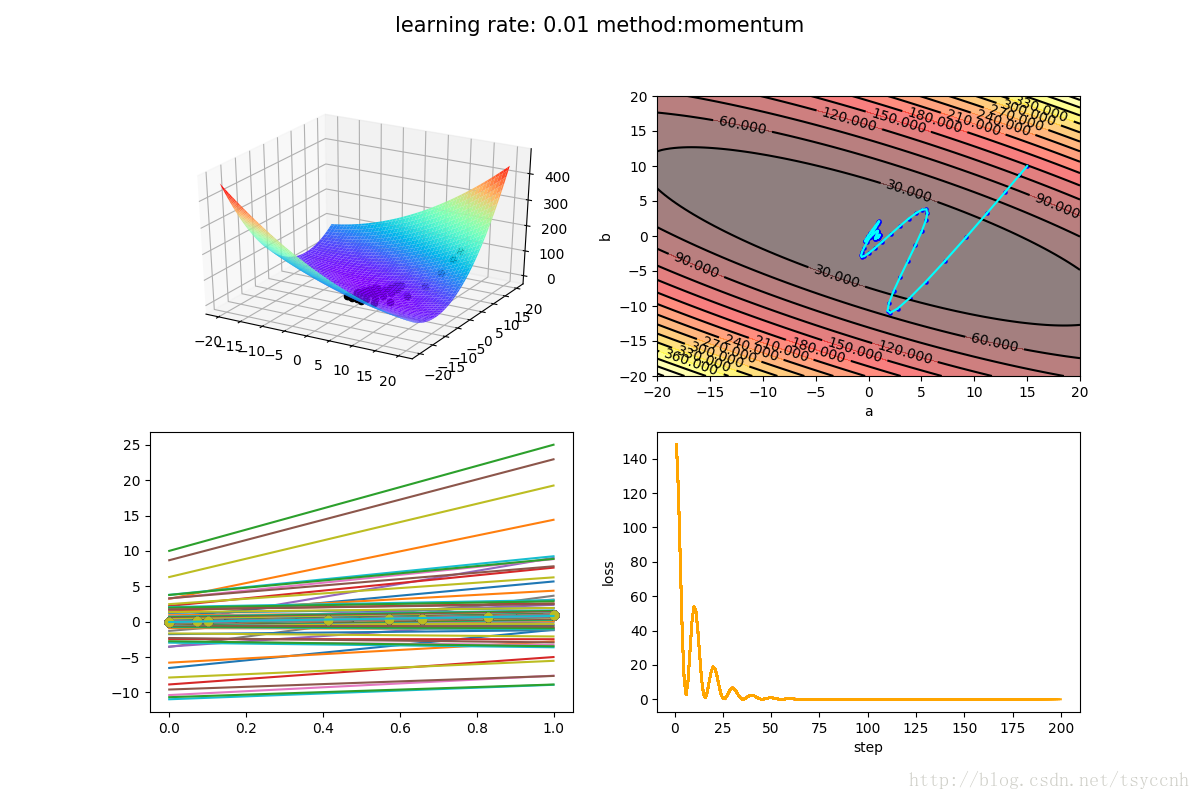
对比Gradient Descent

仔细看右上角的等高线图就可以看见，momentum方法每一步走的都要更远一些。由于累加了动量，会带着之前的速度向前方冲去。比如一开始loss冲入了山谷，由于有之前的动量，继续朝着对面的山坡冲了上去。随着动量的更新，慢慢地最终收敛到了最小值。

注：对比图可能看起来GD算法要好于momentum方法，这仅仅是由于数据集比较简单。本文旨在从理论和实际实验中去学习momentum方法，不对结果对比做太多讨论。实验的结果往往和数据集、参数选择有很大关系。

本文实验代码：https://github.com/tsycnh/mlbasic/blob/master/p4%20momentum.py

深度学习优化函数详解（5）-- Nesterov accelerated gradient (NAG)

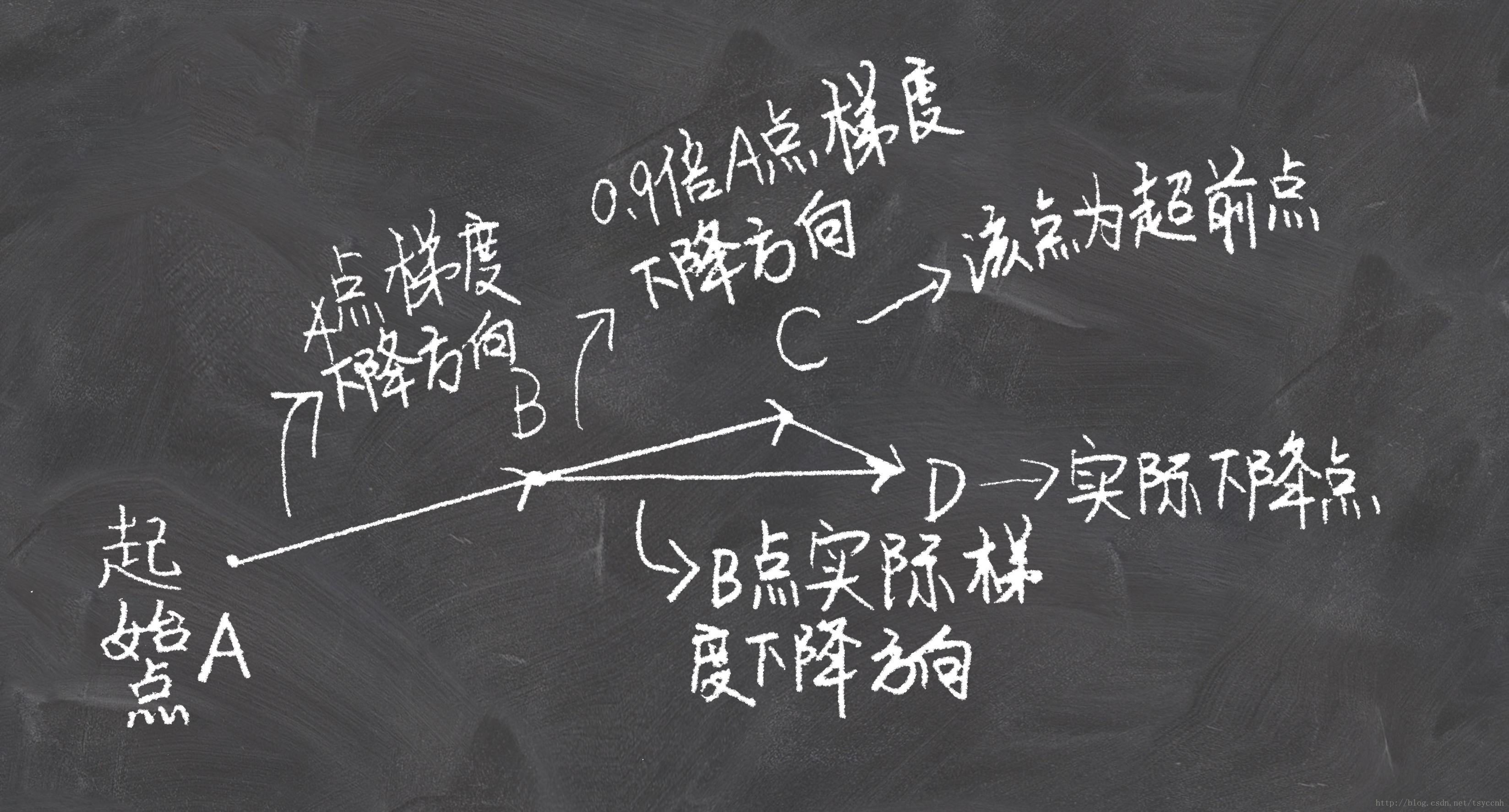
上一篇文章讲解了犹如小球自动滚动下山的动量法（momentum）这篇文章将介绍一种更加“聪明”的滚动下山的方式。动量法每下降一步都是由前面下降方向的一个累积和当前点的梯度方向组合而成。于是一位大神（Nesterov）就开始思考，既然每一步都要将两个梯度方向（历史梯度、当前梯度）做一个合并再下降，那为什么不先按照历史梯度往前走那么一小步，按照前面一小步位置的“超前梯度”来做梯度合并呢？如此一来，小球就可以先不管三七二十一先往前走一步，在靠前一点的位置看到梯度，然后按照那个位置再来修正这一步的梯度方向。如此一来，有了超前的眼光，小球就会更加”聪明“, 这种方法被命名为Nesterov accelerated gradient 简称 NAG。

↑这是momentum下降法示意图

↑这是NAG下降法示意图
看上面一张图仔细想一下就可以明白，Nesterov动量法和经典动量法的差别就在B点和C点梯度的不同。

公式推导

上图直观的解释了NAG的全部内容。
第一次看到NAG的梯度下降公式的时候我是懵的，梯度下降的流程比较明白，公式上不太理解。后来推导了好半天才得到NAG的公式，下面就把我推导的过程写出来。我推导公式的过程完全符合上面NAG的示意图，可以对比参考。
记 vt 为第t次迭代梯度的累积

v0=0

v1=η∇θJ(θ)

v2=γv1+η∇θJ(θ−γv1)

↓

vt=γvt−1+η∇θJ(θ−γvt−1)

参数更新公式

θnew=θ−vt

公式里的 −γvt−1 就是图中B到C的那一段向量， θ−γvt−1 就是C点的坐标（参数）
γ 代表衰减率， η 代表学习率。

实验

实验选择了学习率 η=0.01 , 衰减率 γ=0.9

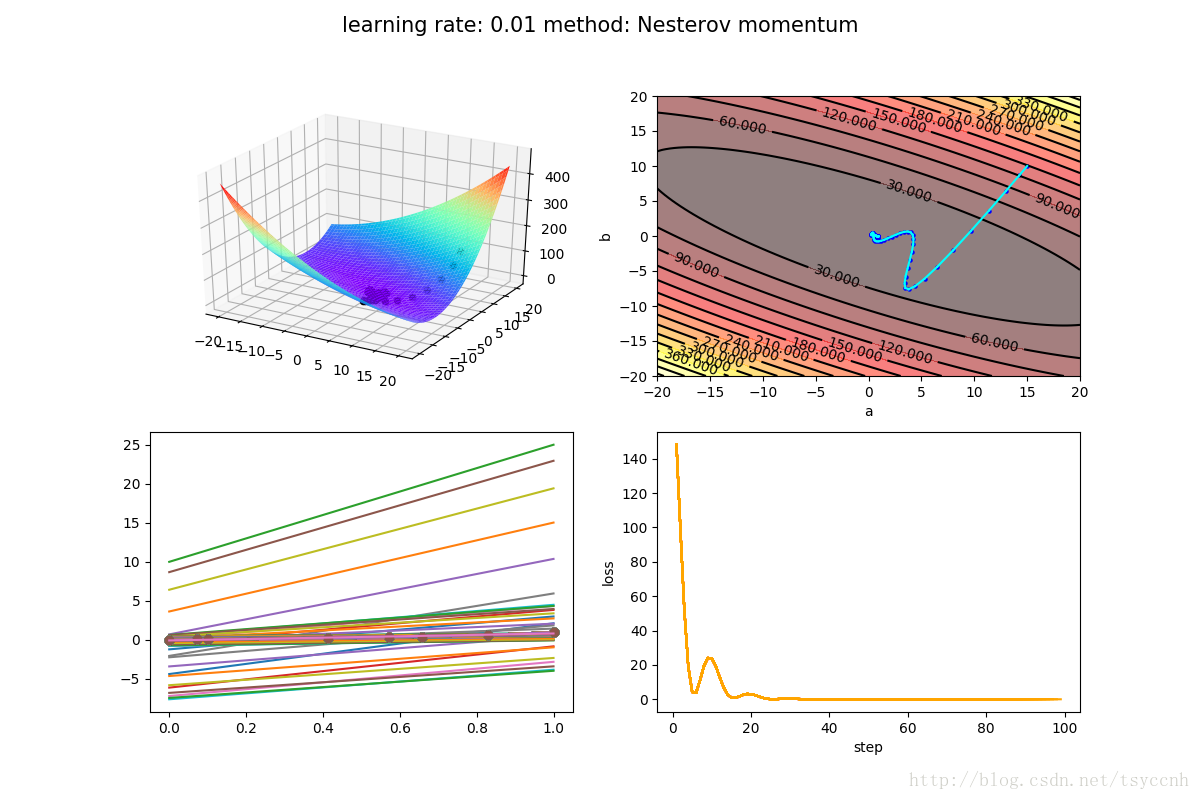
↑ 这是Nesterov方法

↑ 这是动量法（momentum)

没有对比就没有伤害，NAG方法收敛速度明显加快。波动也小了很多。实际上NAG方法用到了二阶信息，所以才会有这么好的结果。

实验源码下载 https://github.com/tsycnh/mlbasic/blob/master/p5%20Nesterov%20momentum.py

深度学习优化函数详解（6）-- adagrad

前面的一系列文章的优化算法有一个共同的特点，就是对于每一个参数都用相同的学习率进行更新。但是在实际应用中各个参数的重要性肯定是不一样的，所以我们对于不同的参数要动态的采取不同的学习率，让目标函数更快的收敛。
adagrad方法是将每一个参数的每一次迭代的梯度取平方累加再开方，用基础学习率除以这个数，来做学习率的动态更新。这个比较简单，直接上公式。

公式推导

∇θiJ(θ) 表示第 i 个参数的梯度，对于经典的SGD优化函数我们可以这样表示

θi_new=θi−η∇θiJ(θ)

adagrad这样表示

θi,t+1=θi,t−ηGi,t+ϵ−−−−−−√∇θi,tJ(θ)

t代表每一次迭代。 ϵ 一般是一个极小值，作用是防止分母为0 。 Gi,t 表示了前 t 步参数 θi 梯度的累加

Gi,t=Gi,t−1+∇θi,tJ(θ)

简化成向量形式

θt+1=θt−ηGt+ϵ−−−−−√∇θtJ(θ)

容易看出，随着算法不断的迭代， Gt 会越来越大，整体的学习率会越来越小。所以一般来说adagrad算法一开始是激励收敛，到了后面就慢慢变成惩罚收敛，速度越来越慢。

实验

实验取 η=0.2,ϵ=1e−8

可以看出收敛速度的确是特别慢（在该数据集下），最重要的原因就是动态学习率处于一个单向的减小状态，最后减到近乎为0的状态。

实验源码：https://github.com/tsycnh/mlbasic/blob/master/p6%20adagrad.py