城市人口与房产价格的关联性分析

系统简介

随着国家经济的高速发展，人们生活水平的不断提高，房价和人口数量的增长都成为了人们关注的重点。本篇论文的研究目的主旨在于利用概率论与数理统计学的相关理论和知识来研究房价与人口是否互相影响。现实意义则是建立的房价预测模型能够在可接受的误差范围之内预测房价拐点，并提出一些有价值的建议。本文先从了解国内人口状况与房价状况的发展背景，通过收集2010-2018年期间关于人口数据与房价数据来了解并简单分析人口与房价的关系，然后使用matlab进行多项式拟合建立房价预测模型，并且对城市人口与房价进行回归建模以及显著性分析并得出结论，最后对人口以及房价提出可应用建议。

关键词 城市人口 房产价格 回归建模 房价预测 MATLAB

1.研究背景

世界上人口最多的发展中国家当然是中国。虽然国土面积在全世界排名位居第三位，但是人口的数量居世界第一位，中国经济社会发展中许多矛盾和问题都与人口密切相关。人口问题是制约中国国内经济与社会发展的关键因素和主要问题。本文主要研究城市人口与房产价格的变化是否有关系，直观看来，房价的涨跌和购房者与供房者的供需关系有关：人口增长会影响房价，且对房价的增加产生非常重要的作用，人口在涨，房价必定涨，人口增加的慢时，房价会逐渐平稳。当对房产的需求大于当前的房量时，房价会增长；反之（房量大于需求），房价下跌。

2.问题分析

直观感受：人越多，房子需求就越大，价格就越高，人数与房价之间的关系应该是呈现正相关的关系。
因为人口自然增长率=人口出生率-人口死亡率，所以将这三个指标合成一个，即人口自然增长率。本文认为人口的快速增长期和房价的快速增长期可能不再一个时间内，随着人口的增长，房子是刚需产品，人必须要有房子住，人对房子的需求增加，房价随之增加，房地产商看到了巨大的利润，当供小于求时，房价不断增加，人们感觉到房价的压力，人口出生率就会降低，人对房子的需求降低，当供大于求时，房价随之降低。
事实上，商品房价格不仅仅只受到这四个因素的影响，只以这四个因素来预测商品房价格的做法本身是存在误差的。本题在进行讨论分析时，不能仅从数据的角度分析得出结果，得出的结果必须符合人们的正常认识，科学分析人口和房价之间的关系，正是本文的研究目的所在。

3.各个城市数据的简单分析

1231233.1城市选取
本文选取了一线城市北京市以及上海市，二线城市厦门市以及长春市，三线城市镇江市以及廊坊市。本篇论文中的六个城市分级是由第一财经•新一线城市研究所所发布的数据信息来确定的。（详细内容见附录——各线城市详细介绍）

3.2各线城市数据简略分析
一线城市数据（来源于各个城市的年鉴）简单分析
北京市：
表3.2-1 北京市人口以及房价相关数据表
北京市 指标 人口出生率(‰) 人口死亡率(‰) 人口自然增长率(‰) 年末常住人口(万人) 住宅商品房平均销售价格(元/平方米)
2010年 7.48 4.41 3.07 1962 17151
2011年 8.29 4.27 4.02 2019 15517.9
2012年 9.05 4.31 4.74 2069 16553.48
2013年 8.93 4.52 4.41 2115 17854
2014年 9.75 4.92 4.83 2152 18499
2015年 7.96 4.95 3.01 2171 22300
2016年 9.32 5.2 4.12 2173 28489
2017年 9.06 5.3 3.76 2171 34117
2018年 8.24 5.58 2.66 2154 37420.19

图3.2- 1 2010-2018北京市年末常住人口

图3.2-2 北京市人口出生、死亡、自然增长率折线

图3.2-3 2010-2018北京市住宅商品房平均售价
从表3.2-1，图3.2-1，图3.2-2可以看出北京市的人口是在不断增长，但是死亡率也在不断上升，人口数量从2016年起开始不断的下降，房价大致上是在不断上涨的，勉强能得出房价上涨和人口的增长有关。
上海市：
表3.2-2 上海市人口以及房价相关数据
上海市 年份 人口出生率(‰) 人口死亡率(‰) 人口自然增长率(‰) 年末常住人口(万人) 住宅商品房平均销售价格(元/平方米)
2010年 7.05 5.07 1.98 2303 14290
2011年 6.97 5.1 1.87 2347 13565.83
2012年 9.56 5.36 4.2 2380 13869.88
2013年 8.18 5.24 2.94 2415 16192
2014年 8.35 5.21 3.14 2426 16415
2015年 7.52 5.07 2.45 2415 21501
2016年 9 5 4 2420 25910
2017年 8.1 5.3 2.8 2418 24866
2018年 7.2 5.4 1.8 2424 28981.11

图3.2-4 2010-2018上海市年末常住人口

从表3.2-2，图3.2-3，图3.2-4可以看出上海市的人口是在不断增长，但是人口数量从2014年起开始不断的下降，房价大致上是在不断上涨的，勉强能得出房价上涨和人口的增长有关，但是关系可能不大。
由一线城市的两个城可以看出，城市越发达，影响房价的因素越多，北京市（一线城市），上海市的发展趋向于饱和，影响房价的因素太多，发展体量大但发展速度慢，因此房价变化不大。
二线城市数据简单分析：
长春市：
表3.2-3 长春市人口以及房价相关数据
长
春
市 年份 人口出生率(‰) 人口死亡率(‰) 人口自然增长率(‰) 年末常住人口(万人) 住宅商品房平均销售价格(元/平方米)
2010年 10.43 6.61 3.82 767.44 5096.92
2011年 9.36 5.14 4.22 761.7 5969.97
2012年 10.2 12.34 -2.15 756.9 5273.35
2013年 9.17 4.07 5.1 752.67 5728.66
2014年 10.37 5.53 4.84 754.55 5846.69
2015年 7.32 5.17 2.15 753.8 6327.86
2016年 8.24 3.89 4.36 753.4 6017.69
2017年 8.61 15.01 -6.39 748.9 6810.67
2018年 7.5 4.74 2.76 751.29 8091.8

厦门市：
表3.2-4 厦门市人口以及房价相关数据
厦门市 年份 人口出生率(‰) 人口死亡率(‰) 人口自然增长率(‰) 年末常住人口(万人) 住宅商品房平均销售价格(元/平方米)
2010年 12.27 8.01 4.26 353.13 11589.02
2011年 12.24 4.75 7.5 353.13 13424.11
2012年 14.95 3.97 10.98 367 12952.53
2013年 15.89 4.67 11.22 373 14551.18
2014年 16.43 5.09 11.34 381 17777.69
2015年 17.49 4.66 12.83 386 18928.27
2016年 21.32 4.84 16.49 392 25250.67
2017年 24.33 6.09 18.24 401 28052.85

在二线城市长春市数据的图3.2-7与图3.2-8表对比可以看出，常住人口数量在2010-2013年是不断下降，2018年与2010年人口数量对比可以明显看出常住人口下降了16.15万人，而房价却上升了2994.88元/平方米，这样看来影响房价的因素众多，房价的增长并不是随着人口数量的增长而增长的。
三线城市数据简单分析
镇江市：
表3.2-5 镇江市人口以及房价相关数据
镇江市 年份 人口出生率(‰) 人口死亡率(‰) 人口自然增长率(‰) 年末常住人口(万人) 住宅商品房平均销售价格(元/平方米)
2010年 7.86 7.79 0.07 311.41 5151.96
2011年 7.98 6.48 1.5 313.43 5769.07
2012年 8.65 10.55 -2.2 315.48 5280.6
2013年 8.98 7.76 1.1 316.54 5813.51
2014年 8.93 7.15 1.8 317.14 5680.88
2015年 8.61 7.05 1.55 317.65 5210.53
2016年 7.97 6.2 1.77 318.13 6168.18
2017年 9.31 11.76 -2.46 318.63 8327.39
2018年 8.24 8.11 0.13 319.64 9799.47

廊坊市：
表3.2-6 廊坊市人口以及房价相关数据
廊坊市 年份 人口出生率(‰) 人口死亡率(‰) 人口自然增长率(‰) 年末常住人口(万人) 住宅商品房平均销售价格(元/平方米)
2010年 12.79 5.88 8.9 435.88 4869.21
2011年 10.76 5.86 5 440 5070.46
2012年 10.87 5.9 14.1 443.93 5581.08
2013年 11.74 6.45 8.5 446.84 6523
2014年 12 5.68 16.2 452.18 7819
2015年 11.94 5.22 10.7 456.32 8297
2016年 13.02 5.79 13.09 461.5 10655
2017年 14.37 6.13 4.21 474.09 12313
2018年 13 4 9 483.66

图3.2-13 2010-2018廊坊市年末常住人口

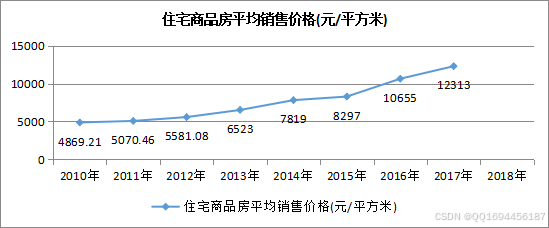
图3.2-14 2010-2018廊坊市住宅商品房平均售价
从三线城市廊坊市数据图13与图14可以看出2010-2018年廊坊市的常住人口数量成总体上升趋势，住宅商品房平均销售价格也在不断成上升趋势。我认为，城市发展水平有限，影响房价的因素少，房价呈现稳定增长的趋势，房价的增长是随着人口的增长而增长的。

4.建立模型过程

444.1建立房价预测模型过程与结果
人口自然增长率=人口出生率-人口死亡率，所以将这三个指标合成一个，即人口自然增长率。本文认为人口的快速增长期和房价的快速增长期可能不再一个时间内，随着人口的增长，房子是刚需产品，人必须要有房子住，人对房子的需求增加，房价随之增加，房地产商看到了巨大的利润，当供小于求时，房价不断增加，人们感觉到房价的压力，人口出生率就会降低，人对房子的需求降低，当供大于求时，房价随之降低。以人口为基准，以人口自然增长率为增长标准，算出后10年人口数据c(i),i=1…10。以住宅商品房平均销售价格(元/平方米)为y，以年末常住人口(万人)为x5。
北京市：
经搜索查得2009年末北京市人口为1247.52万人，以此人口为基准，以人口自然增长率为增长标准，算出后10年人口数据c(i),i=1…10。以住宅商品房平均销售价格(元/平方米)为y，以年末常住人口(万人)为x5，使用MATLAB中的cftool工具箱，通过多项式拟合建立y与c和x5的模型（目标函数）为：

上式为二次多项式曲面公式，总共有6个系数。矩阵形式为：

Matlab运行编码（见附录-房价预测模型）结果如下所示：
Linear model Poly22:

   p00 =   2.517e+04  (7416, 4.292e+04)
   p10 =   1.774e+04  (-1.445e+04, 4.994e+04)
   p01 =  -1.085e+04  (-4.648e+04, 2.479e+04)
   p20 =       -5725  (-2.897e+04, 1.752e+04)
   p11 =        7549  (-6312, 2.141e+04)
   p02 =       -3344  (-1.07e+04, 4015)

Goodness of fit:
SSE: 2.841e+06
R-square: 0.9947
Adjusted R-square: 0.986
RMSE: 973.1
因为R-square和Adjusted R-square都接近1，所以拟合效果很好。通过本公式拟合出来2018年商品房价格为3.7529e+04，与表中给出的数据相差百分之0.29，可见误差非常小，因此拟合效果很好。下面是北京市房价模型运行图其中的黑点是原始点，阴影是公式的三维表示。

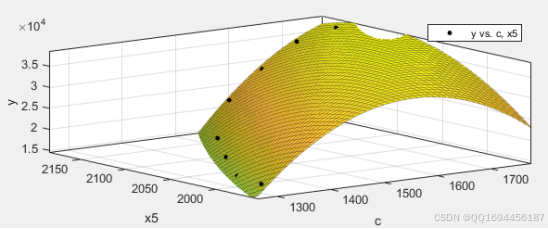
图4.1-1 北京市房价预测模型运行图
上海市：上海市2009年年末人口为1400.70万。
Linear model Poly22:

Coefficients (with 95% confidence bounds):
p00 = -3.269e+06 (-1.856e+07, 1.202e+07)
p10 = -3044 (-1.363e+04, 7540)
p01 = 4720 (-1.383e+04, 2.327e+04)
p20 = -0.1583 (-0.7181, 0.4014)
p11 = 1.501 (-3.443, 6.445)
p02 = -1.481 (-6.842, 3.881)
Goodness of fit:
SSE: 9.052e+06
R-square: 0.9675
Adjusted R-square: 0.9133
RMSE: 1737
因为R-square和Adjusted R-square都接近1，所以拟合效果很好。通过本公式拟合出来2018年商品房价格为2.8378e+04，与表中给出的数据相差百分之2.08，可见误差非常小，因此拟合效果很好。

图4.1-2 上海市房价预测模型运行图
厦门市：厦门市2009年年末人口为177万。
Linear model Poly22:

Coefficients (with 95% confidence bounds):
p00 = 1.244e+06 (-7.838e+06, 1.033e+07)
p10 = 1045 (-1.208e+04, 1.417e+04)
p01 = -7293 (-6.457e+04, 4.999e+04)
p20 = 0.1369 (-4.164, 4.437)
p11 = -2.737 (-43.66, 38.19)
p02 = 10.62 (-79.64, 100.9)
Goodness of fit:
SSE: 3.96e+06
R-square: 0.9917
Adjusted R-square: 0.9779
RMSE: 1149
因为R-square和Adjusted R-square都接近1，所以拟合效果很好。通过本公式拟合出来2018年商品房价格为3.3500e+04，与表中给出的数据相差百分之0.64，可见误差非常小，因此拟合效果很好。

图4.1-3 厦门市房价预测模型运行图

长春市：
长春市2009年年末人口为756.51万。
Linear model Poly22:

Coefficients (with 95% confidence bounds):
p00 = -4.074e+07 (-9.921e+07, 1.774e+07)
p10 = 1.086e+04 (-2614, 2.433e+04)
p01 = 9.572e+04 (-4.43e+04, 2.357e+05)
p20 = -0.4091 (-0.9305, 0.1123)
p11 = -13.44 (-30.42, 3.542)
p02 = -55.85 (-139.2, 27.52)
Goodness of fit:
SSE: 8.773e+05
R-square: 0.8636
Adjusted R-square: 0.6363
RMSE: 540.8
因为R-square和Adjusted R-square都接近1，所以拟合效果很好。通过本公式拟合出来2018年商品房价格为7.7784e+03，与表中给出的数据相差百分之3.87，可见误差非常小，因此拟合效果很好。

图4.1-4 长春市房价预测模型运行图
镇江市：镇江市2009年年末人口为311万。
Linear model Poly22:

Coefficients (with 95% confidence bounds):
p00 = 2.347e+07 (5.722e+06, 4.122e+07)
p10 = 7.201e+04 (-2.732e+04, 1.713e+05)
p01 = -2.214e+05 (-4.146e+05, -2.827e+04)
p20 = 34.06 (-27.33, 95.45)
p11 = -296 (-724.1, 132)
p02 = 499.8 (-9.839, 1009)
Goodness of fit:
SSE: 1.253e+06
R-square: 0.9398
Adjusted R-square: 0.8393
RMSE: 646.2
因为R-square和Adjusted R-square都接近1，所以拟合效果很好。通过本公式拟合出来2018年商品房价格为1.0002e+04，与表中给出的数据相差百分之2.07，可见误差非常小，因此拟合效果很好。

5 镇江市房价预测模型运行图

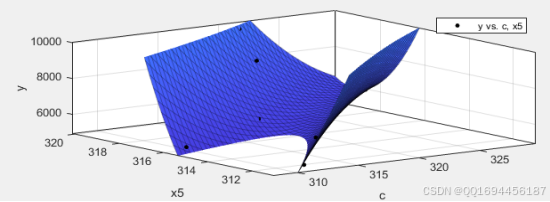
廊坊市：廊坊市2009年年末人口为434万。
Linear model Poly22:

Coefficients (with 95% confidence bounds):
p00 = 4.12e+07 (-1.048e+08, 1.872e+08)
p10 = 1.387e+04 (-3.558e+04, 6.332e+04)
p01 = -2.033e+05 (-9.242e+05, 5.175e+05)
p20 = 1.111 (-2.816, 5.038)
p11 = -34.06 (-155.4, 87.33)
p02 = 250.8 (-638.6, 1140)
Goodness of fit:
SSE: 2.053e+05
R-square: 0.996
Adjusted R-square: 0.986
RMSE: 320.4
因为R-square和Adjusted R-square都接近1，所以拟合效果很好。通过本公式拟合出来2018年商品房价格为1.2314e+04，与表中给出的数据相差接近百分之0，可见误差非常小，因此拟合效果很好。
在这里插入图片描述

图4.1-6 廊坊市房价预测模型运行图
4.2城市人口与房价的回归建模以及显著性分析
使用MATLAB软件，以回归系数和自变量为输入变量，将要拟合的模型写成函数文件myfun.m（见附录-源码1），构建出来的模型（目标函数）为：
然后，用nlinfit计算回归系数，用nlparci计算回归系数的置信区间，用nlpredci 计算预测值及其置信区间，编程文件为myfit.m（见附录-源码2），运行结果为：运行后的结果均方根误差
mse =
2.4462e+07
1、估计系数和置信区间 第一列为估计系数，第二、三列为区间（置信区间95%）
表4.2-1 估计系数以及置信空间
估计系数 置信区间
-2.1132 [-5.2500，1.0236]
-0.1694 [-1.1558，0.8169]
0.7227 [-0.0518，1.4971]
0.0751 [-0.5308，0.6809]
0.0179 [-0.0211，0.0569]
-0.0484 [-0.0865，-0.0103]
0.0058 [-0.0148，0.0265]
-0.0029 [-0.0065，0.0006]
0.0009 [0.0007，0.0011]

5.结论与建议

人口增长会影响房价，且对房价的增加产生非常重要的作用，人口在涨，房价必定涨，人口增加的慢时，房价会逐渐平稳。廊坊市的房价预测效果最好，长春市的预测结果最差，北京市的预测结果较小。城市越发达，影响房价的因素越多，因为数据中值给出人口有关的参数，所以预测结果越不稳定。北京市（一线城市）的发展趋向于饱和，影响房价的因素太多，发展体量大但发展速度慢，因此房价变化不大，长春市（二线城市）的发展速度快，房价变化大，影响房价的因素也较多，因此预测结果最不精确，廊坊市（三线城市）体量小，城市发展水平有限，影响房价的因素少，房价呈现稳定增长的趋势，因此预测结果最精准。
从需求端来看，第一类城市应适度控制人口净流入，防止房价 上涨过快，同时对拥有多套住房的本地居民或外地 投资者，政府也应当落实限购政策，严格征收房产税。而且政府应当合理分流人口，鼓励人口流向三、四线城市，在加快三、四线城市建设和小城镇建设的 同时，出台当地城镇化的优惠政策，增加就业岗位，改善居住环境，提高居民生活水平。总之，对不同类型的城市实施更具针对性的宏观调控政策、人口流动政策和城镇化政策，将房价控制在合理的区间，既防止快速上涨，又防范急剧下跌，保证国民经济实现 稳定、协调和可持续增长。

致谢

时间流逝如白驹过缝，转眼四年的大学生活即将结束，这四年的大学生涯让我学习到了很多知识，毕业论文论文的完成更是让我学习良多，如释重负。
历时半载，从论文选题到搜集资料，从开题报告、写初稿到反复修改，期间经历了喜悦、聒噪、痛苦和彷徨，在写作论文的过程中心情是如此复杂。如今，伴随着这篇毕业论文的最终成稿，复杂的心情烟消云散，自己甚至还有一点成就感。
我首先要感谢我的论文指导老师，赵俊老师。赵俊老师指出的每一个问题，每一个指导思想，都给了我一种严谨的感觉。最令我印象深刻的是老师的态度严谨。无论格式规范，论文的主要观点还是文章结构，老师都不厌倦给我及时的帮助，使我能够成功地完成论文写作工作。期间老师对我论文的研究方向做出了指导性的意见和推荐，在论文撰写过程中及时对我遇到的困难和疑惑给予悉心指点，提出了许多有益的改善性意见，投入了大量精力。在这段时间里，我学到了很多知识也有很多感受，独立的学习和调研，查看相关的资料和书籍，让自己头脑中模糊的概念逐渐清晰。经过四个多月的努力，我最后完成了论文的写作，从选题到论文文章的完成，每走一步对我来说都是新的尝试与挑战。
此外，还要感谢朋友以及同学们在论文编写中带给的大力支持和帮忙，给我带来极大的启发。也要感谢参考文献中的作者们，透过他们的研究文章，使我对研究课题有了很好的出发点。
最后，谢谢论文评阅老师们的辛苦工作。衷心感谢我的家人、朋友，以及同学们，真是在他们的鼓励和支持下我才得以顺利完成此论文。并对于所有帮助过我的同学、朋友表示诚挚的谢意，在四年里互相学习，互相帮忙，共同度过了一段美好难忘的时光。

附录

各线城市详细介绍
一线城市指的是在全国政治、经济等社会活动中处于重要地位并具有主导作用和辐射带动能力的大都市。其主要体现在城市发展水平、综合经济实力、辐射带动能力、对人才吸引力、信息交流能力、国际竞争能力、科技创新能力、交通通达能力等各层面，一线城市在生产、服务、金融、创新、流通、综合商业指数等全国社会活动中起到引领和辐射等主导功能。中国大陆的一线城市一般指北京、上海、广州、深圳。
二线城市（Second-tier City）一般多为省会城市、东部地区的经济强市或经济发达地区的区域性中心城市。二线城市有一定的经济基础，商业活跃度相对较强，对大公司、大品牌和优秀人才具有一定的吸引力，也正在或者即将成为未来几年大公司布局的重点。
三线城市（Third-tier City）是根据城市规模、人口数量、经济发展水平和GDP总量等多个指标综合评估的具有战略意义、经济较发达、经济总量较大的大中城市。三线城市大部分城市规模较大，中心城区非农业人口多数在100万人以上，城市基础设施、商业配套设施和交通设施相对比较完善，居民拥有一定的消费能力，居民的生活水平一般相对比较富裕，城市拥有一定的支柱产业，产业结构相对比较合理，对某些行业的大型企业具有一定的吸引力，但城市综合竞争力仍有待进一步提高。三线城市一般多为东部地区的经济较发达城市，中部地区的省域副中心城市、区域性中心城市或经济强市，西部地区的省会城市。
房价预测模型代码（matlab）

Clc
clear
a=[数据];
y=a(1:9,6);
x1=a(1:9,1);
x2=a(1:9,2);
x3=a(1:9,3);
x4=a(1:9,4);
x5=a(1:9,5);
b=1247.52;
c=zeros(1,9);
for i=2:9
    c(1)=b*(1+x4(1)*0.01)
    c(i)=c(i-1)*(1+x4(i)*0.01);
end
 (3.7529e+04-37420.19)/37420.19
function [fitresult, gof] = createFit(c, x5, y)
 [xData, yData, zData] = prepareSurfaceData( c, x5, y );
ft = fittype( 'poly22' );
 [fitresult, gof] = fit( [xData, yData], zData, ft );
figure( 'Name', 'untitled fit 1' );
h = plot( fitresult, [xData, yData], zData );
legend( h, 'untitled fit 1', 'y vs. c, x5', 'Location', 'NorthEast', 'Interpreter', 'none' );
xlabel( 'c', 'Interpreter', 'none' );
ylabel( 'x5', 'Interpreter', 'none' );
zlabel( 'y', 'Interpreter', 'none' );
grid on

插入数据表
城市人口与房价的回归模型建立MATLAB代码
北京市 指标 人口出生率(‰) 人口死亡率(‰) 人口自然增长率(‰) 年末常住人口(万人) 住宅商品房平均销售价格(元/平方米)
2010年 7.48 4.41 3.07 1962 17151
2011年 8.29 4.27 4.02 2019 15517.9
2012年 9.05 4.31 4.74 2069 16553.48
2013年 8.93 4.52 4.41 2115 17854
2014年 9.75 4.92 4.83 2152 18499
2015年 7.96 4.95 3.01 2171 22300
2016年 9.32 5.2 4.12 2173 28489
2017年 9.06 5.3 3.76 2171 34117
2018年 8.24 5.58 2.66 2154 37420.19
上海 2010年 7.05 5.07 1.98 2303 14290
2011年 6.97 5.1 1.87 2347 13565.83
2012年 9.56 5.36 4.2 2380 13869.88
2013年 8.18 5.24 2.94 2415 16192
2014年 8.35 5.21 3.14 2426 16415
2015年 7.52 5.07 2.45 2415 21501
2016年 9 5 4 2420 25910
2017年 8.1 5.3 2.8 2418 24866
2018年 7.2 5.4 1.8 2424 28981.11
厦门市 2010年 12.27 8.01 4.26 353.13 11589.02
2011年 12.24 4.75 7.5 353.13 13424.11
2012年 14.95 3.97 10.98 367 12952.53
2013年 15.89 4.67 11.22 373 14551.18
2014年 16.43 5.09 11.34 381 17777.69
2015年 17.49 4.66 12.83 386 18928.27
2016年 21.32 4.84 16.49 392 25250.67
2017年 24.33 6.09 18.24 401 28052.85
2018年 19.69 4.04 15.65 411 33715.14
长春市 2010年 10.43 6.61 3.82 767.44 5096.92
2011年 9.36 5.14 4.22 761.7 5969.97
2012年 10.2 12.34 -2.15 756.9 5273.35
2013年 9.17 4.07 5.1 752.67 5728.66
2014年 10.37 5.53 4.84 754.55 5846.69
2015年 7.32 5.17 2.15 753.8 6327.86
2016年 8.24 3.89 4.36 753.4 6017.69
2017年 8.61 15.01 -6.39 748.9 6810.67
2018年 7.5 4.74 2.76 751.29 8091.8
镇江市 2010年 7.86 7.79 0.07 311.41 5151.96
2011年 7.98 6.48 1.5 313.43 5769.07
2012年 8.65 10.55 -2.2 315.48 5280.6
2013年 8.98 7.76 1.1 316.54 5813.51
2014年 8.93 7.15 1.8 317.14 5680.88
2015年 8.61 7.05 1.55 317.65 5210.53
2016年 7.97 6.2 1.77 318.13 6168.18
2017年 9.31 11.76 -2.46 318.63 8327.39
2018年 8.24 8.11 0.13 319.64 9799.47
廊坊市 2010年 12.79 5.88 8.9 435.88 4869.21
2011年 10.76 5.86 5 440 5070.46
2012年 10.87 5.9 14.1 443.93 5581.08
2013年 11.74 6.45 8.5 446.84 6523
2014年 12 5.68 16.2 452.18 7819
2015年 11.94 5.22 10.7 456.32 8297
2016年 13.02 5.79 13.09 461.5 10655
2017年 14.37 6.13 4.21 474.09 12313
2018年 13 4 9 483.66
源码 1

myfun.m ：
function yy=fun(b,x)
yy=b(1)+b(2)*(x(:,1))+b(3)*x(:,2)+b(4)*x(:,3)+...
    +b(5)*(x(:,1).^2)+b(6)*(x(:,2).^2)+b(7)*(x(:,3).^2)+...
    b(8)*x(:,1).*x(:,2).*x(:,3)+b(9)*x(:,4);

f(b,x)= b1+ b2*x1+ b3*x2+ b4*x3+ b5*x12+ b7*x22+ b8*x32+b9*x4

源码 2

myfit.m ：
% 参考链接 https://blog.csdn.net/qq_29831163/article/details/89555708
clc
clear
close all;
load('data')
%加载数据
x=data(:,1:4);
y=data(:,end);
% 回归系数的初值,随机数
beta= rand(1,9);
yy=myfun(beta,x);
% 拟合
[beta_out,r,J,COVB,mse]=nlinfit(x,y,@myfun,beta);    
beta_out
mse
% 求置信区间
betaci=nlparci(beta_out,r,'Jacobian',J);
% 打印回归系数，及其置信区间（第一列是回归系数，第二三列是置信区间）
betaa=[beta_out',betaci] 
% 预测
[yy,delta]=nlpredci(@myfun,x,beta_out,r,'Jacobian',J); 
r=corrcoef(y,yy);     % 求相关系数r
figure()
plotregression(yy,y)   % 并且画图r
% https://m.wenda.so.com/q/1368281333060338
%回归分析， 可查看检验值
regstats(y,yy,'quadratic')
figure()
plot(y);hold on;plot(yy)
title('回归示例')
legend('True','Pred');
通过regstats函数做回归分析（可查找出F检验，D-W检验的检验值），以查看F检验的值为例：