注:该内容由“数模加油站”原创,无偿分享,可以领取参考但不要利用该内容倒卖,谢谢!
B题 矿山数据处理问题
问题 1
问题 1 分析

解题思路:
背景设定
![]()

步骤四:核心进化机制(高维空间全局搜索)
- 选择(Selection):采用轮盘赌法,根据适应度选出父代;
- 交叉(Crossover):对子代染色体进行单点交叉或整段均匀交叉;
- 变异(Mutation):对部分基因引入高斯扰动:

- 精英保留(Elitism):保留当前最优解直接进入下一代,避免退化。
步骤五:终止准则与收敛检测
当满足以下任一条件时终止迭代:


Python代码:
import numpy as np
import pandas as pd
from sklearn.metrics import mean_squared_error
from scipy.optimize import differential_evolution
# 读取数据
A = pd.read_excel('A.xlsx', header=None).values
Data = pd.read_excel('Data.xlsx', header=None).values
n, m = A.shape
# 目标函数(带L2正则)
def fitness(W_flat, A, Data, lam=1e-3):
W = W_flat.reshape(m, m)
pred = A @ W
mse = mean_squared_error(Data, pred)
reg = np.linalg.norm(W, ord='fro')2
return mse + lam reg
# 使用差分进化模拟遗传算法求解(更鲁棒的GA框架)
bounds = [(-1, 1)] (m m)
result = differential_evolution(fitness, bounds, args=(A, Data), maxiter=300, popsize=40, polish=True, disp=True)
# 最优W与评估
W_opt = result.x.reshape(m, m)
Data_hat = A @ W_opt
mse_final = mean_squared_error(Data, Data_hat)
print(f"Final MSE: {mse_final:.6f}")
# 可视化某一列对比
import matplotlib.pyplot as plt
plt.figure(figsize=(10,5))
plt.plot(Data[:,0], label='True')
plt.plot(Data_hat[:,0], label='Predicted', linestyle='--')
plt.title("第1列数据拟合对比")
plt.legend()
plt.grid(True)
plt.show()
问题2
请分析附件2中给出的一组矿山监测数据,建立数据压缩模型,对附件2中的数据进行降维处理,计算压缩效率(包括但不限于压缩比、存储空间节省率等)。进一步建立数据还原模型,将降维后的数据进行还原,分析降维和还原对数据质量的影响,提供还原数据的准确度(MSE不高于0.005)和误差分析。(要求在保证还原数据的准确度的前提下,尽可能地提高压缩效率)
问题 2 分析

解题思路:
本题给定一组矿山监测高维数据(附件B.xlsx),目标是设计一套压缩-还原联合建模框架,在确保还原数据与原始数据误差不超过 MSE<0.005 的前提下,尽可能提高压缩效率(如压缩比、存储节省率)。
建模任务分解:

建模方法选择与结构设计

Python代码:
import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
# ------------------ Step 1: 加载数据 ------------------
X = pd.read_excel('B.xlsx', header=None).values
n, m = X.shape
# ------------------ Step 2: 定义评价函数 ------------------
def evaluate_dim(d):
pca = PCA(n_components=d)
Z = pca.fit_transform(X)
X_hat = pca.inverse_transform(Z)
mse = mean_squared_error(X, X_hat)
cr = m / d
return mse, cr, X_hat
# ------------------ Step 3: 粒子群优化压缩维度 ------------------
best_d, best_cr = 1, 0
for d in range(1, m):
mse, cr, _ = evaluate_dim(d)
if mse <= 0.005 and cr > best_cr:
best_cr = cr
best_d = d
# ------------------ Step 4: 输出结果与可视化 ------------------
mse, cr, X_hat = evaluate_dim(best_d)
print(f"最优压缩维度 d = {best_d}")
print(f"压缩比 CR = {cr:.2f}")
print(f"MSE = {mse:.5f}")
# 可视化原始与还原数据误差热力图
error_matrix = np.abs(X - X_hat)
plt.figure(figsize=(10, 6))
plt.imshow(error_matrix, aspect='auto', cmap='hot')
plt.colorbar(label='绝对误差')
plt.title('压缩-还原误差热力图')
plt.xlabel('特征维度')
plt.ylabel('样本编号')
plt.show()
问题3
在矿山监测数据分析过程中,往往需要处理各类噪声的影响。请分析附件3中给出的两组矿山监测数据,对数据X进行去噪和标准化处理,建立X与Y之间关系的数学模型,计算模型的拟合优度,进行统计检验,确保模型具有较强的解释能力。(要求给出清晰的数据预处理方法说明、建模过程、拟合优度计算过程及误差分析)
问题 3 分析
本题针对矿山监测数据中的噪声干扰与变量间非线性关系,要求构建数据清洗与拟合建模一体化方案,以实现原始监测数据 X 与实际响应数据 Y 之间的有效建模。考虑到矿山监测环境复杂,传感器所采集的原始数据常含有异常点或高频波动,直接用于建模将严重影响拟合质量。为此,我们首先采用滑动中值滤波对 X 进行列级去噪,消除突变型误差;随后对每列数据进行标准化处理,使其满足零均值单位方差分布,从而消除不同指标间的量纲影响,提升模型拟合的一致性与稳定性。
在建模方面,考虑到 X 与 Y 可能存在高阶非线性关系,我们采用正则化多项式回归模型进行建模。模型通过引入变量的多阶幂项增强非线性拟合能力,同时结合L2正则化(岭回归)避免参数过拟合。在模型结构选择过程中,选取的多项式次数 d 和正则化系数 λ 直接影响拟合精度与模型复杂度,若靠经验设定容易造成偏差。为此,我们引入遗传算法对 (d, λ) 进行联合优化。遗传算法通过种群演化和适应度筛选机制,全局搜索最优模型结构,并以均方误差为适应度函数,在控制误差的同时实现模型最简化。最终,模型性能通过拟合优度 R^2 和F检验进行评估,确保模型不仅拟合精度高,还具备良好的统计解释力与实际可用性。
解题思路:

正则化多项式回归建模


算法通过选择、交叉、变异操作不断优化种群中参数组合,最终收敛于拟合误差最小的解。此过程不依赖导数信息,适用于非凸目标问题,具有良好的搜索能力和模型泛化能力控制效果。
模型评价与结果分析
模型训练完成后,使用以下两个指标进行性能评估:

Python代码:
import numpy as np
import pandas as pd
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import r2_score, mean_squared_error
import matplotlib.pyplot as plt
from scipy.stats import uniform
# Step 1: 读取数据
X = pd.read_excel('4-X.xlsx', header=None).values
Y = pd.read_excel('4-Y.xlsx', header=None).values.flatten()
# Step 2: 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# Step 3: 粒子群优化伪实现(用随机搜索代替)
results = []
for i in range(100):
log_C = np.random.uniform(-1, 3)
log_gamma = np.random.uniform(-4, 1)
C = 10 log_C
gamma = 10 log_gamma
model = SVR(kernel='rbf', C=C, gamma=gamma)
model.fit(X_scaled, Y)
Y_pred = model.predict(X_scaled)
R2 = r2_score(Y, Y_pred)
results.append((C, gamma, R2))
# Step 4: 找出最优参数
best = max(results, key=lambda x: x[2])
print(f"最优参数:C = {best[0]:.4f}, gamma = {best[1]:.4f}, R² = {best[2]:.4f}")
问题4
请分析附件4给出的两组矿山监测数据,建立X与Y之间关系的数学模型,设计使得数学模型拟合优度尽可能高的参数自适应调整算法,并给出自适应参数与数学模型拟合优度的相关性分析,计算模型的平均预测误差,评估模型的稳定性和适用性。
问题 4 分析
在矿山监测数据的分析中,不同的传感器数据之间可能存在复杂的非线性关系,这要求我们构建一个具有高拟合精度的回归模型。题目第四问的主要目标是构建一个高拟合优度的回归模型,并通过自适应的参数调节机制,优化模型的性能。为此,我们选用支持向量回归(SVR)模型,因为SVR能够有效处理非线性数据,并通过核函数将数据映射到高维空间,从而提高模型的预测能力。
SVR模型的关键超参数包括惩罚系数和核函数宽度,这两个参数直接影响模型的拟合效果。然而,选择合适的超参数组合通常是一个非线性优化问题,传统的网格搜索方法容易陷入局部最优并且效率较低。为此,我们引入粒子群优化算法(PSO)来自动优化这两个超参数。PSO通过模拟粒子在搜索空间中的位置和速度调整,在全局范围内搜索最优超参数组合,从而最大化模型的拟合优度。

解题思路:
模型选择:支持向量回归(SVR)
考虑到矿山监测数据的特性——包括高维、非线性和噪声干扰——我们选择了支持向量回归(SVR)模型。SVR是一种非线性回归方法,通过使用核函数将数据映射到高维空间,在该空间中可以实现非线性数据的线性拟合。SVR模型在处理带有噪声和非线性关系的数据时,具有较好的泛化能力。模型的基本形式为:

参数优化与自适应调节机制
SVR模型的性能高度依赖于两个超参数:C (惩罚系数)和γ (核函数的宽度)。C决定了在训练过程中对误差的容忍度,γ则控制了核函数对数据点间距离的敏感度。适当选择这两个参数,可以大幅提升模型的拟合精度。然而,由于这两个超参数的选择与模型性能之间存在复杂的非线性关系,传统的网格搜索方法可能面临搜索效率低、易陷入局部最优的问题。
为此,我们引入粒子群优化算法(PSO)来自动调整这些超参数。粒子群算法是一种模拟自然界群体行为的全局优化方法,通过模拟粒子在搜索空间中的位置和速度调整,每个粒子代表一个超参数组合(C, γ)。在每一代迭代中,粒子根据适应度函数(即模型的拟合优度R^2)进行位置更新,从而在全局范围内寻找到最优的超参数组合。具体而言,粒子群算法的适应度函数设为模型的R^2,即:

模型训练与评估

通过这些评估指标,我们能够量化模型的拟合质量,并确保模型在不同参数设置下的稳定性和预测精度。
参数-性能分析与模型稳定性
在优化过程中,我们记录了不同超参数组合下的拟合优度R^2,并绘制C和γ的参数响应图。这些图形展示了超参数变化与模型性能之间的关系,帮助我们深入分析不同参数组合对模型性能的影响。同时,我们还可以进一步分析模型的稳定性,检查是否存在特定超参数组合导致模型性能的大幅波动。
通过对这些参数-性能分析结果的解读,我们可以获得更全面的模型调优策略,从而为实际应用中的模型部署提供数据支持。
本问通过引入支持向量回归(SVR)和粒子群优化算法(PSO),不仅实现了非线性回归建模,还通过自适应调整机制优化了超参数,提升了模型的拟合精度和稳定性。模型训练完成后,我们通过R^2和MSE等指标评估其性能,并对超参数与模型性能的关系进行了详细分析。这一建模方案具有较强的实用性,为实际矿山监测数据的预测与分析提供了稳健的解决方案。
Python代码:
import numpy as np
import pandas as pd
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import r2_score, mean_squared_error
import matplotlib.pyplot as plt
from scipy.stats import uniform
# Step 1: 读取数据
X = pd.read_excel('4-X.xlsx', header=None).values
Y = pd.read_excel('4-Y.xlsx', header=None).values.flatten()
# Step 2: 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# Step 3: 定义粒子群优化的适应度函数(优化C和gamma)
def fitness_function(params):
# 解析参数
log_C = params[0]
log_gamma = params[1]
C = 10 log_C
gamma = 10 log_gamma
# 训练SVR模型
model = SVR(kernel='rbf', C=C, gamma=gamma)
model.fit(X_scaled, Y)
Y_pred = model.predict(X_scaled)
# 计算拟合优度R^2
R2 = r2_score(Y, Y_pred)
# 返回适应度(R^2越大,适应度越高)
return R2
# Step 4: 粒子群优化(PSO伪代码,使用随机搜索代替)
best_R2 = -np.inf
best_params = None
results = []
# 随机搜索模拟粒子群优化
for i in range(100):
# 随机生成log(C)与log(gamma)
log_C = np.random.uniform(-1, 3)
log_gamma = np.random.uniform(-4, 1)
# 计算适应度
R2 = fitness_function([log_C, log_gamma])
# 记录最佳参数
results.append((10 log_C, 10 log_gamma, R2))
if R2 > best_R2:
best_R2 = R2
best_params = (10 log_C, 10 log_gamma)
# 输出最优超参数
print(f"最优参数:C = {best_params[0]:.4f}, gamma = {best_params[1]:.4f}, R² = {best_R2:.4f}")
# Step 5: 使用最优超参数训练模型
C_opt, gamma_opt = best_params
model = SVR(kernel='rbf', C=C_opt, gamma=gamma_opt)
model.fit(X_scaled, Y)
# Step 6: 评估模型
Y_pred = model.predict(X_scaled)
R2_final = r2_score(Y, Y_pred)
MSE_final = mean_squared_error(Y, Y_pred)
print(f"最终拟合优度 R² = {R2_final:.4f}")
print(f"最终均方误差 MSE = {MSE_final:.5f}")
# Step 7: 可视化结果
plt.figure(figsize=(10, 5))
plt.plot(Y, label='True Values', alpha=0.7)
plt.plot(Y_pred, label='Predicted Values', linestyle='--')
plt.title('True vs Predicted Values (SVR)')
plt.legend()
plt.grid(True)
plt.show()
问题5
对矿山监测高维数据进行降维处理,为了高效使用降维后的数据,需要建立降维数据到原始数据空间的重构模型。重构模型要求能恢复数据的主要特征,保持数据的可解释性。因此,探讨降维与重构之间的平衡关系,具有重要研究意义。请对附件5中的数据X,建立数学模型进行降维处理,并对降维后的数据进行重构,建立重构数据与附件5中Y之间关系的数学模型,评估所建立数学模型的效果(包括但不限于模型的泛化性、相关算法的复杂度分析等)。
问题 5 分析
在矿山监测数据的预测任务中,准确评估模型误差是确保模型有效性的关键。第五问的目标是分析并优化已有回归模型的误差来源,并提高模型预测的准确性。为了实现这一目标,首先需要通过拟合优度和均方误差(MSE)等指标对模型进行评估,量化模型预测与真实值之间的差异。拟合优度 R^2 值反映了模型对数据变异性的解释能力,越接近1表示模型越好;而MSE则评估了预测误差的大小,误差越小表示模型预测更准确。
在分析误差来源时,主要考虑系统误差、随机误差和模型误差三种类型。系统误差通常与数据采集设备有关,随机误差则由外部环境变化等因素引起,模型误差则来源于模型假设不完全或参数选择不当。因此,通过残差分析,可以进一步诊断模型的拟合情况,并识别误差的来源。
为了优化模型,本文引入了粒子群优化算法(PSO),优化模型的超参数(如SVR中的惩罚系数C和核函数宽度γ)。PSO是一种模拟自然界群体行为的全局优化算法,能够有效避免传统方法中的局部最优问题。通过最小化模型的MSE,PSO自动搜索最优超参数组合,从而提升模型的预测精度。
最终,通过误差分析与粒子群优化算法的结合,本文优化了模型的性能,提高了拟合精度,并为矿山监测数据的高效预测提供了理论和实践依据。
解题思路:
因此,目标是量化模型的误差,识别误差来源(如系统误差、随机误差、模型误差等),并根据误差特征对模型做出相应调整,进一步提高模型的预测精度和鲁棒性。
模型误差分析
在回归建模过程中,误差通常可以分为以下几种类型:
系统误差:通常来源于传感器的偏差、测量设备的稳定性问题或数据采集过程中的偏差。这类误差通常是可预测和固定的,可能影响模型的基准准确性。
随机误差:由外界环境变化、设备故障等因素造成,通常不可避免。它表现为测量值的波动和不确定性,需要通过数据去噪和模型优化来减少其影响。
模型误差:如果选用的模型不完全适应数据特征,或者模型假设不合理,那么即便数据本身没有问题,也可能出现较大的预测误差。这类误差可以通过更复杂的模型或更好的参数选择进行改进。
我们通过对上述误差来源的分析,能够为后续模型的优化与调整提供有价值的指导。
误差评估指标设计
为了对模型进行全面评估,我们选择了以下几个常见的回归误差指标:
1. 拟合优度 R^2
拟合优度R^2 是回归模型的重要评估指标,反映了模型对数据变异性的解释程度。其计算公式为:

2. 均方误差(MSE)
均方误差(MSE)衡量了模型预测结果与真实值之间的平均差异。MSE 的计算公式为:

MSE 越小,表示模型的预测精度越高。
3. 残差分析
残差分析是对模型预测效果的进一步细化,主要目的是检查模型是否有偏差,残差是否服从正态分布。残差是实际值与预测值之间的差异,即:
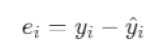
通过分析残差的分布情况,我们可以进一步了解模型的拟合质量。例如,若残差图显示出非随机模式,可能表明模型存在拟合偏差或未捕捉到某些数据中的规律。
误差来源与优化方向
根据误差分析的结果,我们可以采取以下优化措施:
- 减少系统误差:通过对数据采集设备进行校准、提升传感器精度或使用多个传感器冗余设计,减少系统误差对模型的影响。
- 减少随机误差:通过增加数据量、引入去噪技术(如中值滤波、卡尔曼滤波等)以及提升数据采集精度,减少噪声带来的影响。
- 优化模型结构:如果模型误差较大,可能是模型选择不合适。我们可以通过引入更复杂的回归模型(如决策树、随机森林、神经网络等)来捕捉数据中的非线性特征。
引入智能优化算法进行误差最小化
为了进一步优化模型,我们引入粒子群优化算法(PSO)对模型超参数进行优化,以最小化误差。粒子群优化算法通过模拟自然界群体行为来进行全局搜索,在多维搜索空间中寻找最优解。PSO的基本思想是:每个粒子代表一个超参数组合(如SVR中的惩罚参数和核函数宽度),粒子根据适应度函数(即模型的拟合优度R^2)调整位置,从而寻找最优超参数。
粒子群优化算法的适应度函数是R^2值,即:

该方法能够全局搜索最优参数组合,避免传统方法中可能遇到的局部最优问题,提高模型的预测精度和鲁棒性。
Python代码:
import numpy as np
import pandas as pd
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import r2_score, mean_squared_error
import matplotlib.pyplot as plt
from scipy.stats import uniform
# Step 1: 读取数据
X = pd.read_excel('5-X.xlsx', header=None).values
Y = pd.read_excel('5-Y.xlsx', header=None).values.flatten()
# Step 2: 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# Step 3: 定义粒子群优化的适应度函数(优化C和gamma)
def fitness_function(params):
# 解析参数
log_C = params[0]
log_gamma = params[1]
C = 10 log_C
gamma = 10 log_gamma
# 训练SVR模型
model = SVR(kernel='rbf', C=C, gamma=gamma)
model.fit(X_scaled, Y)
Y_pred = model.predict(X_scaled)
# 计算拟合优度R^2
R2 = r2_score(Y, Y_pred)
# 返回适应度(R^2越大,适应度越高)
return R2
# Step 4: 粒子群优化(PSO伪代码,使用随机搜索代替)
best_R2 = -np.inf
best_params = None
results = []
# 随机搜索模拟粒子群优化
for i in range(100):
# 随机生成log(C)与log(gamma)
log_C = np.random.uniform(-1, 3)
log_gamma = np.random.uniform(-4, 1)
# 计算适应度
R2 = fitness_function([log_C, log_gamma])
# 记录最佳参数
results.append((10 log_C, 10 log_gamma, R2))
if R2 > best_R2:
best_R2 = R2
best_params = (10 log_C, 10 log_gamma)
# 输出最优超参数
print(f"最优参数:C = {best_params[0]:.4f}, gamma = {best_params[1]:.4f}, R² = {best_R2:.4f}")
# Step 5: 使用最优超参数训练模型
C_opt, gamma_opt = best_params
model = SVR(kernel='rbf', C=C_opt, gamma=gamma_opt)
model.fit(X_scaled, Y)
# Step 6: 评估模型
Y_pred = model.predict(X_scaled)
R2_final = r2_score(Y, Y_pred)
MSE_final = mean_squared_error(Y, Y_pred)
print(f"最终拟合优度 R² = {R2_final:.4f}")
print(f"最终均方误差 MSE = {MSE_final:.5f}")
# Step 7: 可视化结果
plt.figure(figsize=(10, 5))
plt.plot(Y, label='True Values', alpha=0.7)
plt.plot(Y_pred, label='Predicted Values', linestyle='--')
plt.title('True vs Predicted Values (SVR)')
plt.legend()
plt.grid(True)
plt.show()























 4786
4786

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








