HDU5478Can you find it(快速幂)

题意：给你C,k1,k2,b1，按字典序输出满足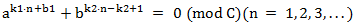的所有(a,b)对

解题思路：因为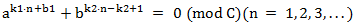对于任意n均满足，故n=1的情况也是符合的，故可得

①

而n=2的情况也是符合的，可得

②

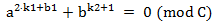
因为①式mod C = 0 ,所以①式乘以一个数mod C 仍为0，不妨①式*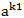，可得

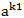
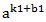
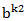
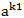
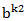
所以，我们只需遍历一遍a的取值(1~C-1)，利用快速幂计算出，以及，再根据式①可以算出b，再用一次快速幂求出，比较(mod C)是否等于(mod C)即可

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll pow_mod (ll x, int n, int mod)
{
    ll ret = 1;
    while (n)
    {
        if (n&1) ret = ret * x % mod;
        x = x * x % mod;
        n >>= 1;
    }
    return ret;
}

int main ()
{
    int cas = 1, C, k1, b1, k2;
    while (scanf("%d%d%d%d", &C, &k1, &b1, &k2) == 4)
    {
        printf("Case #%d:\n", cas++);
        int cnt = 0;
        for (int a = 1; a < C; a++)
        {
            int b = C - pow_mod(a, k1+b1, C);
            if (pow_mod(a, k1, C) == pow_mod(b, k2, C))
            {
                printf("%d %d\n", a, b);
                cnt++;
            }
        }
        if (cnt == 0)
            printf("-1\n");
    }
    return 0;
}