数据流异常检测的概念漂移现象

---

前言

模型在发生退化时，问题的源头不仅是模型和算法本身，新的数据也会影响模型的退化，在数据流异常检测任务中，对于数据影响模型的一个重要的概念是“漂移”，漂移的场景和特征多种多样，整体分为两类：
Data drift: change in data distributions.
Concept drift : change in relationships.

更新日期：2024/01/18

一、关于概念漂移

• Data drift:
  
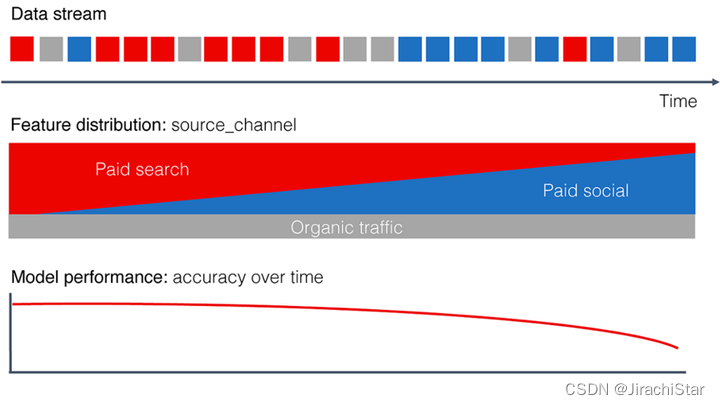
  目标任务是预测电商平台在投放广告后，用户购买商品的可能性，Paid search是在搜索引擎中投放广告，Paid social是在社交媒体中投放广告，数据的分布在电商平台改变营销策略之后发生有意义的改变，模型适应不了新出现的数据，自然而然发生退化，这种情况属于数据漂移。
• Concept drift:
  
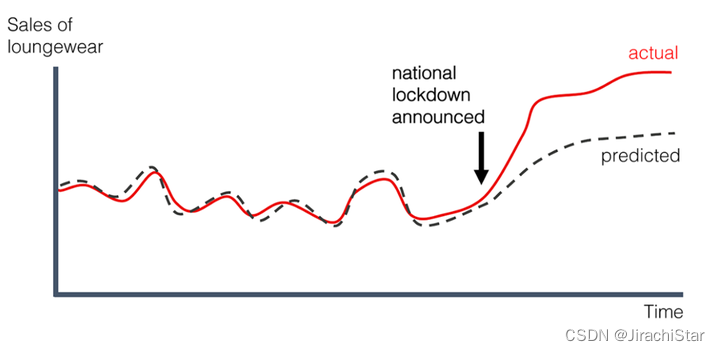
  发生概念漂移的情况可能是渐变的也可能是突变的。
  慢一点的情况：
  宏观经济条件不断变化。随着一些借款人拖欠贷款，信用风险被重新定义。计分模型需要学习它。
  突变的情况：
  covid-19突然的增长式爆发导致政府颁布隔离政策，人们对于居家服的需求剧增。

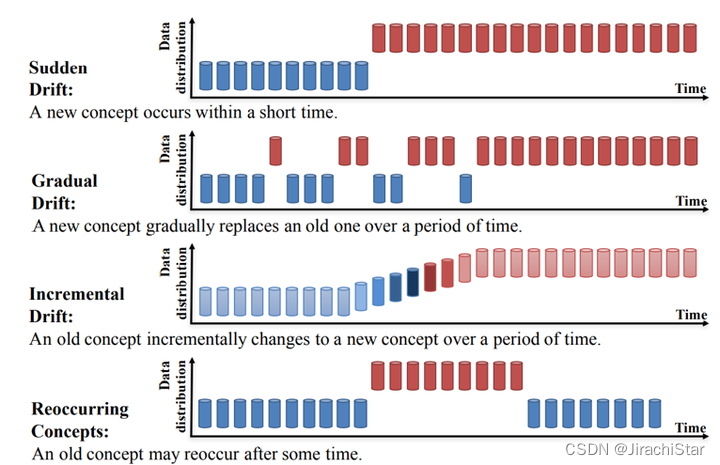
1. Sudden Drift:
   模型突然从一个主题或概念转移到另一个主题或概念，没有明显的过渡或连接。典型情况例如新政策执行、紧急情况等外部环境突变的场景。
2. Gradual Drift:
   模型慢慢地离开了原来的主题或概念，逐渐转移到另一个主题或概念。例如电视的销量预测，随着人们用手机，用电脑，电视的销量逐渐发生了变化。
3. Incremental Drift:
   模型逐渐添加了与原来的主题或概念不相关的信息，最终新概念取代旧概念。例如组织结构在质量优化中渐进调整，概念属于增量变化。
4. Recurring Concepts： 反复使用相同的概念或主题，而不是在不同的上下文中探索新的想法或主题，一般呈现季节性、周期性变化，但也有非周期性。例如旅行社可能会在圣诞节期间安排不同的流程来吸引客户，这是周期性的体现。但同时受到市场环境的影响，这是非周期性的体现。

二、数据流异常检测的概念漂移

一个基本的基于数据流的异常检测模型如下图所示。该模型接收一个不断增长的数据流，对每个数据点计算异常得分，并根据设定的阈值来判断是否为异常数据。模型的参数 ${\theta }_M$ 会不断更新，以适应新的数据流。
对检测过程进行描述，模型会将新来的数据进行分批处理：1）先用一批数据进行推断，计算出该批数据中每个数据点的异常得分，并与$threshold$相比较，判断是否为异常数据；2）然后再用这批数据来更新模型参数。这个过程中，模型的学习和测试是交替进行的，即每检测完一批数据就会进行一次参数更新，以便更好地适应新的数据流；3）模型不断输出所有被判定为异常的数据点。

在数据流异常检测中发生概念漂移的现象是指，如果在某个时间点 $t$ 上，输入数据点 $X$ 和它们的标签 $y$ 的联合概率分布发生了变化，即 $P_t(X,y)\ne P_{t+1}(X,y)$，则称发生了概念漂移。根据联合概率分布的定义，这种概念漂移可能由以下三种情况之一引起：
(i) 数据分布发生变化，即 $P_t(X)\ne P_{t+1}(X)$；
(ii) 异常决策边界发生变化，即 $P_t(y\mid X)\ne P_{t+1}(y\mid X)$；
(iii) 同时发生 (i) 和 (ii) 两种情况。
数据分布和异常决策边界都是由模型的参数 ${\theta }_M$体现的， 一旦发生概念漂移，当前的异常检测模型就会变得过时，需要更新以适应新的概念。由于概念漂移可能以“突然（Sudden ）”、“渐进（Gradual）”、“增量（Incremental）”和“周期性（Recurring）”等不同形式发生，因此需要一个多功能机制来处理所有这些形式的漂移。

三、一些解决方法

• 无监督概念漂移检测方法的分类：

1. 基于统计的方法：使用统计测试来检测数据分布中的变化。例如，它们可能会计算数据流中的两个窗口（时间段）的统计特性，并使用诸如Hoeffding Bound之类的测试来确定这些统计特性是否有显著变化。

2. 基于窗口的方法：通过比较固定大小或可调整大小的数据窗口来检测漂移。如果新窗口的数据与旧窗口显著不同，则可能表明发生了概念漂移。

3. 基于图的方法：使用图结构来表示数据项之间的关系，并检测这些关系随时间的变化。

4. 基于模型的方法：这些方法通过监控学习模型的性能或其参数的变化来检测漂移。例如，如果模型的预测错误率突然增加，可能表明概念已经发生变化。

Rosana Noronha Gemaque等人，根据漂移的发生形式对无监督概念漂移检测方法进行分类：

• 基于批处理的检测方法分为整批检测和部分批处理检测两种方法
• 基于在线方法的检测分为固定窗口（在训练实例上使用固定的参考窗口）和滑动窗口（窗口滑动到未标记漂移样本中，可能与检测窗口重叠）两种方法
  

1.漂移检测方法（DDM）

第一阶段是由一个landmark时间窗口实现的，窗口的起点是固定的，而窗口的终点将在收到新的数据实例后被扩展。当新数据进来，DDM会检测时间窗口内的整体在线错误率是否显著增加。如果观察到的错误率变化达到警告level，DDM开始建立一个新的学习器,同时使用旧的学习器进行预测。如果变化达到了漂移level，旧的学习者将被新的学习者取代，用于进一步的预测任务。
为了获得在线错误率，DDM需要一个分类器来进行预测。这个过程将训练数据转换为模型，这是第二阶段（数据建模）。
第三阶段的测试统计数据构成在线错误率。
第四阶段估计在线错误率的分布和计算警告水平、漂移水平的阈值。
后续的ADaptive WINdowing (ADWIN)，Relativized Discrepancy (RD)、Information-Theoretic Approach (ITA)都受DDM影响。只是在第一阶段窗口选择上各有不同。

2.ARCUS

链接： Adaptive Model Pooling for Online Deep Anomaly Detection from a Complex Evolving Data Stream

1）模型可靠性计算

在给定的上下文中，有两个集合：$M\left(B_{Curr};{\theta }_M\right)$ 和 $M\left(B_{\text{Last }};{\theta }_M\right)$。前者代表当前数据流的异常分数集合，而后者代表用于更新模型的上一批次数据的异常分数集合。模型$M$的统计显著性差异是指这两个集合之间的差异程度，这可以用来衡量模型对当前批次的可靠性。为了量化这种显著性，采用了基于Hoeffding不等式的均值差异界（参见定理1）。这个方法被广泛用于检测流数据的统计变化。

• 公式1：（基于Hoeffding不等式的均值差异界）给出了两个独立随机变量$X$和$Y$的样本均值差异的概率。如果$X$和$Y$的取值范围（异常分数）在$\left[a_{\min },a_{\max }\right]$内，那么样本均值差异大于$ϵ$的概率被限制在不等式中。代入得到新公式，其中 $b$ 是集合大小，$ϵ$ 是两个集合的平均值之间的差异，$s_{\max }$ 和 $s_{\min }$ 分别是两个集合中最大和最小的异常分数。
  Pr ⁡ { ∣ X ˉ − Y ˉ ∣ ≥ ϵ } ≤ e − 2 ϵ 2 ( n − 1 + m − 1 ) ( a max ⁡ − a min ⁡ ) 2 . \operatorname{Pr}{\{|\bar{X}-\bar{Y}| \geq \epsilon\}} \leq e^{\frac{-2 \epsilon^2}{\left(n^{-1}+m^{-1}\right)\left(a_{\max }-a_{\min }\right)^2}} . Pr{∣Xˉ−Yˉ∣≥ϵ}≤e(n−1+m−1)(amax​−amin​)2−2ϵ2​.
  $$\mathrm{Pr}|\bar{X}-\bar{Y}|\ge ϵ\le e^{\frac{-2{ϵ}^2}{\left(b^{-1}+b^{-1}\right){\left(s_{\max }-s_{\min }\right)}^2}}=e^{\frac{-b{ϵ}^2}{{\left(s_{\max }-s_{\min }\right)}^2}},$$
• 公式2：用来计算模型的可靠性 $r_M$，它表示样本均值差异高于或等于 $ϵ$ 的概率上限。
  $$r_M=e^{\frac{-b{ϵ}^2}{{\left(s_{\max }-s_{\min }\right)}^2}},$$

接下来，定义了一个概念驱动的异常分数 $C_P(x)$，它是基于模型池 $P$ 中的每个模型 $M_i$ 的可靠性 $r_{M_i}$ 和标准化的异常分数来计算的。具体来说，对于每个模型 $M_i$，将其标准化的异常分数减去当前批次的平均值，然后除以当前批次的标准差，然后乘以其可靠性 $r_{M_i}$，最后将所有模型的结果相加得到异常分数 $C_P(x)$。
$$C_P(x)=\sum _{i=1}^k{r}_{M_i}\left(\frac{M_i\left(x;{\theta }_{M_i}\right)-\mathrm{avg}\left(M_i\left(B;{\theta }_{M_i}\right)\right)}{\mathrm{std}\left(M_i\left(B;{\theta }_{M_i}\right)\right)}\right).$$

2）模型池可靠性评估

• 对于模型池$P$中的每个模型$M_i$，使用模型可靠性定义中的概率$1-r_M$来估计其不可靠性。
• 定义整个模型池的可靠性$R_P$为$1$ 减去所有模型不可靠的概率的乘积。

3）模型池的更新触发条件

• 当有新的批次包含从未见过的概念时，模型池中的模型可能无法正确进行推断。因此，ARCUS使用一个显著性水平$1-\alpha$来判断是否需要更新模型池。
• 如果模型池中至少有一个高度可靠的模型（即$r_M>\alpha$），则保持模型池不变；否则，进行模型池的调整（一般来说$\alpha$默认为0.95）。

4） 模型池的调整

• 当触发更新时，ARCUS首先使用当前批次创建一个新模型$M_{new}$。
• 通过递归地将$M_{new}$与模型池$P$中与其相似度超过阈值$\gamma$的最相似模型进行合并，形成一个紧凑的模型池$P^{\ast }$。

在ARCUS中，$\gamma$ 是一个用于判断两个模型相似度的阈值。 $\gamma$ 的文中默认设置为 0.8，以允许模型池同时具有多样性（即 $\gamma >0.5$）和紧凑性（即 $\gamma <1$）。具体而言，$\gamma$ 的选择要考虑到模型池中的模型在相似性上的两个因素：

1. 多样性（Diversity）：

   • 当 $\gamma >0.5$ 时，表示模型池中的模型对于相同概念的数据具有一定的多样性，即它们在表示数据的方式上有差异。

2. 紧凑性（Compactness）：

   • 当 $\gamma <1$ 时，表示模型池中的模型之间的相似度足够高，使得它们可以在某种程度上被视为相似或相关的模型。

在这里，选择 $\gamma =0.8$ 的目的是在保持模型池多样性的同时，确保模型之间的相似性不会过于低，以防止模型过于分散。这种设置通常是基于经验和实验结果的平衡，确保模型池既能适应新概念，又能保持一定的一致性。

5）模型的相似度度量和合并（Model Similarity and Merging）

• 使用中心核对齐（Centered Kernel Alignment，CKA）度量两个模型的相似性。CKA是用于神经网络表示相似性的适当指标，不受正交变换和各向同性缩放的影响。
• 如果两个模型的相似性超过阈值$\gamma$，则将它们进行权重平均合并，以减少模型池中的冗余和防止过拟合。

---

总结

---

参考文章

1. 知乎：概念漂移（concept drift）总结
2. R. P. J. C. Bose, W. M. P. van der Aalst, I. Žliobaitė and M. Pechenizkiy, “Dealing With Concept Drifts in Process Mining,” in IEEE Transactions on Neural Networks and Learning Systems, vol. 25, no. 1, pp. 154-171, Jan. 2014, doi: 10.1109/TNNLS.2013.2278313.
3. Susik Yoon, Youngjun Lee, Jae-Gil Lee, Byung Suk Lee:Adaptive Model Pooling for Online Deep Anomaly Detection from a Complex Evolving Data Stream. CoRR abs/2206.04792 (2022)