自适应控制
14-基于Lyapunov稳定性理论设计模型参考自适应控制器
一、相关的稳定性理论
-
平衡点:无外力作用于系统时,系统将保持不变;
-
稳定: ∥ x ( t ; x 0 , t 0 ) − x e ∥ < ϵ \left\| x(t;x_0,t_0)-x_e \right\| < \epsilon ∥x(t;x0,t0)−xe∥<ϵ;
一致稳定:
渐进稳定: ( 1 ) x e 为稳定点; ( 2 )若初始状态满足 ∥ x 0 − x e ∥ < δ ( t 0 ) ,就有 lim t → ∞ ∥ x ( t ; x 0 , t 0 ) − x e ∥ = 0 (1)x_e为稳定点;(2)若初始状态满足\left\| x_0-x_e \right\|<\delta(t_0),就有\lim_{t\rightarrow \infin}\left\| x(t;x_0,t_0)-x_e \right\|=0 (1)xe为稳定点;(2)若初始状态满足∥x0−xe∥<δ(t0),就有limt→∞∥x(t;x0,t0)−xe∥=0
一致渐近稳定:
-
Figure:

-
几个经典的结论
-
正定函数和半正定函数的定义:
一个连续可微的函数 V : R n → R V:R^n \rightarrow R V:Rn→R ,在包含原点“ 0 0 0 ”的区域: U ∈ R n U \in R^n U∈Rn 内被称为是正定的,如果以下两个条件成立:
V ( 0 ) = 0 ; V ( x ) > 0 , x ∈ U 且 x ≠ 0 V(0)=0 \ \ ;\ \ V(x)>0,x \in U 且 x \neq 0 V(0)=0 ; V(x)>0,x∈U且x=0
以上函数被称为是半正定的,如果 V ( x ) > 0 V(x)>0 V(x)>0 被替换为 V ( x ) ≥ 0 V(x) \geq 0 V(x)≥0 。 -
时不变系统(Time Invariant Systems)的稳定性理论:
对用如下状态方程描述的动力学系统:
X ˙ = f ( X ) \dot X=f(X) X˙=f(X)
设 X = 0 X=0 X=0 是以上系统的一个平衡点,即 f ( 0 ) = 0 f(0)=0 f(0)=0 ,如果存在包含此平衡点的集合 D ⊂ R n D \subset R^n D⊂Rn 以及在此集合上定义的具有以下条件的连续可微函数:
V : D → R V ( 0 ) = 0 且 V ( X ) > 0 , X ∈ D − { 0 } V:D \rightarrow R \\ V(0)=0 且 V(X)>0,X \in D-\{0\} V:D→RV(0)=0且V(X)>0,X∈D−{0}
在此基础上,如果沿以上方程轨线的
V ˙ ( X ) = ∂ V T ∂ x d x d t = ∂ V T ∂ x f ( x ) = − W ( x ) ≤ 0 , X ∈ D \dot V(X) =\frac{\partial V^T}{\partial x} \frac{\rm dx}{\rm dt} =\frac{\partial V^T}{\partial x}f(x) =-W(x) \leq 0,X \in D V˙(X)=∂x∂VTdtdx=∂x∂VTf(x)=−W(x)≤0,X∈D
则平衡点 x ( t ) = 0 x(t)=0 x(t)=0 稳定; 如果进一步有:
V ˙ ( X ) < 0 , X ∈ D − 0 \dot V(X)<0,X \in D-{0} V˙(X)<0,X∈D−0
则平衡点 x ( t ) = 0 x(t)=0 x(t)=0 渐进稳定; 如果进一步有:
V ˙ ( X ) < 0 ,并且当 ∥ x ∥ → ∞ 时, V ( X ) → ∞ \dot V(X)<0,并且当 \left\| x \right\| \rightarrow \infin 时,V(X) \rightarrow \infin V˙(X)<0,并且当∥x∥→∞时,V(X)→∞
则平衡点 x ( t ) = 0 x(t)=0 x(t)=0 全局渐进稳定。 -
时变系统的稳定性定理:
-
K 类函数的定义:
连续函数 α : [ 0 , a ) → [ 0 , ∞ ) \alpha:[0,a) \rightarrow [0,\infin) α:[0,a)→[0,∞) 被称为是属于 K 类函数,如果它严格递增(Strictly Increasing)且 α ( 0 ) = 0 \alpha(0)=0 α(0)=0 。
-
定理:
对用如下状态方程描述的动力学系统
X ˙ = f ( X , t ) \dot X=f(X,t) X˙=f(X,t)
设 X = 0 X=0 X=0 是以上系统的平衡点,即 f ( 0 , t ) = 0 f(0,t)=0 f(0,t)=0 ,以及:
D = { x ∈ R n , ∥ x ∥ < r } D=\{ x \in R^n,\left\| x \right\| <r \} D={x∈Rn,∥x∥<r}
如果存在一个连续可微的函数 V V V ,满足
α 1 ( ∥ x ∥ ) ≤ V ( x , t ) ≤ α 2 ( ∥ x ∥ ) d V d t = ∂ V ∂ t + ∂ V T ∂ t f ( x , t ) ≤ 0 , ∀ t ≥ 0 \alpha_1(\|x\|) \leq V(x,t) \leq \alpha_2(\|x\|) \\ \frac{\rm dV}{\rm dt} = \frac{\partial V}{\partial t} + \frac{\partial V^T}{\partial t}f(x,t) \leq 0, \forall t \geq 0 α1(∥x∥)≤V(x,t)≤α2(∥x∥)dtdV=∂t∂V+∂t∂VTf(x,t)≤0,∀t≥0
其中, α 1 , α 2 , α 3 \alpha_1,\alpha_2,\alpha_3 α1,α2,α3 为 K 类函数,则平衡点 x ( t ) = 0 x(t)=0 x(t)=0 一致稳定。
-
-
有界收敛集定理:
对用如下状态方程描述的动力学系统
X ˙ = f ( X , t ) \dot X=f(X,t) X˙=f(X,t)
令 D = { x ∈ R n , ∥ x ∥ < r } D=\{ x \in R^n,\| x \|<r \} D={x∈Rn,∥x∥<r} ,并假设 f ( X , t ) f(X,t) f(X,t) 在 D × [ 0 , ∞ ) D \times [0,\infin) D×[0,∞) 上满足 Lipschitz 条件。如果存在一个连续可微的函数 V V V ,满足
α 1 ( ∥ x ∥ ) ≤ V ( x , t ) ≤ α 2 ( ∥ x ∥ ) \alpha_1(\| x \|) \leq V(x,t) \leq \alpha_2(\| x \|) α1(∥x∥)≤V(x,t)≤α2(∥x∥)
并且
d V d t = ∂ V ∂ t + ∂ V T ∂ x f ( x , t ) ≤ − W ( x ) ≤ 0 , ∀ t ≥ 0 , ∀ x ∈ D \frac{\rm dV}{\rm dt} =\frac{\partial V}{\partial t}+\frac{\partial V^T}{\partial x}f(x,t) \leq -W(x) \leq 0, \forall t \geq 0,\forall x \in D dtdV=∂t∂V+∂x∂VTf(x,t)≤−W(x)≤0,∀t≥0,∀x∈D
其中, α 1 , α 2 \alpha_1,\alpha_2 α1,α2 为定义在 [ 0 , ∞ ) [0,\infin) [0,∞) 上的 K 类函数,并且 W ( x ) W(x) W(x) 在 D D D 上连续。 进一步,如果 d V d t \frac{\rm dV}{\rm dt} dtdV 关于时间 t t t 一致连续,则对于满足不等式
∥ x ( t 0 ) ∥ < α 2 − 1 ( α 1 ( r ) ) \| x(t_0) \| < \alpha_2^{-1} (\alpha_1(r)) ∥x(t0)∥<α2−1(α1(r))
的初值的方程 X ˙ = f ( X , t ) \dot X=f(X,t) X˙=f(X,t) 所有的解都有界,并且有
W ( x ( t ) ) → 0 , t → ∞ W(x(t)) \rightarrow 0,t \rightarrow \infin W(x(t))→0,t→∞- 定理说明系统所有的状态都有将有界,并且趋于集合 { x ∈ D ∣ W ( x ) = 0 } \{ x \in D | W(x)=0 \} {x∈D∣W(x)=0} ;
- 定理要求如果 d V d t \frac{\rm dV}{\rm dt} dtdV 关于时间 t t t 一致连续,而关于这一点的一个充分条件是 V ¨ \ddot V V¨ 有界。
-
Kalman-Yakubovich 引理:
-
正实传递函数(Positive Real Transfer Function)的定义
称带实系数有理传递函数 G G G 为正实的,如果:
R e ( G ( s ) ) ≥ 0 , R e ( s ) ≥ 0 \rm{Re}(G(s)) \geq 0,\rm{Re} (s) \geq 0 Re(G(s))≥0,Re(s)≥0
称传递函数 G G G 为严格正实的,如果存在 ε > 0 \varepsilon >0 ε>0 使得 G ( s − ε ) G(s-\varepsilon) G(s−ε) 是正实的。 -
正实性质(PR)的条件:
一个带实系数有理传递函数 G G G 为正实的,当且仅当满足以下条件时成立:
- 该函数在右半平面没有极点(开右半平面);
- 如果函数在虚轴上或在无穷大上有极点,它们都是具有正残差的简单极点;
- G ( s ) G(s) G(s) 的实部沿着 i ω i\omega iω 轴是非负的,即 R e ( G ( i ω ) ) ≥ 0 \rm{Re}(G(i\omega)) \geq 0 Re(G(iω))≥0 。
-
严格正实(SPR)的条件:
- 该函数在闭右半复平面上没有极点;
- 沿虚轴 i ω i\omega iω ,有 R e ( G ( i ω ) ) > 0 \rm{Re}(G(i\omega)) > 0 Re(G(iω))>0 。(注:并没有要求 ω → ∞ \omega \rightarrow \infin ω→∞ 时, R e ( G ( i ω ) ) > 0 \rm{Re}(G(i\omega))>0 Re(G(iω))>0)
-
严格正实的性质:
- 频域:传递函数的 Nyquist 图处于一、四象限内(闭右复平面);(注:并非说 Nyquist 图处于一、四象限一定是严格正实的)
- 时域:传递函数的相对阶为 0 o r ± 1 0 or \pm 1 0or±1 ;(相对阶: D e g ( d ) − D e g ( n ) Deg(d)-Deg(n) Deg(d)−Deg(n))
- 如果 G ( s ) G(s) G(s) 为 PR(SPR),则 1 / G ( s ) 1/G(s) 1/G(s) 也为 PR(SPR)。
-
Kalman-Yakubovich引理
设线性定常系统
X ˙ = A X + B U Y = C X \dot X=AX+BU \\ Y=CX X˙=AX+BUY=CX
完全可控、可观测,则传递函数
G ( s ) = C ( s I − A ) − 1 B G(s)=C(sI-A)^{-1}B G(s)=C(sI−A)−1B
严格正实的充要条件是存在正定矩阵 P , Q P,Q P,Q 使得:
A T P + P A = − Q B T P = C A^TP+PA=-Q \\ B^TP=C ATP+PA=−QBTP=C
-
-
二、设计实例
-
例1
-
参考模型:
d y m d t = − a m y m + b m u c \frac{\rm dy_m}{\rm dt} =-a_my_m+b_mu_c dtdym=−amym+bmuc
被控对象:
d y d t = − a y + b u \frac{\rm dy}{\rm dt} = -ay+bu dtdy=−ay+bu
其中, a , b a,b a,b 为未知的常数,其中 b b b 的符号要求已知。 -
选择自适应律: u ( t ) = θ 1 u c ( t ) − θ 2 y ( t ) u(t)=\theta_1u_c(t)-\theta_2y(t) u(t)=θ1uc(t)−θ2y(t)
-
设计过程:
S 1 : 引入误差 e = y − y m ⟶ y m = y − e S 2 : 对误差求导 d e d t = d y d t − d y m d t = − a y + b u − ( − a m y m + b m u c ) = − a y + b ( θ 1 u c − θ 2 y ) + a m ( y − e ) − b m u c = − a m e − ( b θ 2 + a − a m ) y + b ( θ 1 − b m ) u c S 3 : 简记 { θ 1 ′ = b θ 1 − b m θ 2 ′ = b θ 2 + a − a m ,有 d e d t = − a m e − ( b θ 2 ′ ) y + b ( θ 1 ′ ) u c S 4 : 取能量函数 V ( e , θ 1 ′ , θ 2 ′ ) = 1 2 [ e 2 + 1 b γ ( θ 2 ′ ) 2 + 1 b γ ( θ 1 ′ ) 2 ] S 5 : 对能量函数求导数 d V d t = e ⋅ d e d t + 1 b γ θ 2 ′ d θ 2 ′ d t + 1 b γ θ 1 ′ d θ 1 ′ d t = − a m e 2 + θ 2 ′ ( θ ˙ 2 ′ b γ − y e ) + θ 1 ′ ( θ ˙ 1 ′ b γ + u c e ) S 6 : 令 { θ ˙ 2 ′ b γ − y e = 0 → θ ˙ 2 ′ = b γ y e θ ˙ 1 ′ b γ − u c e = 0 → θ ˙ 1 ′ = b γ u c e S 7 : d 2 V d t 2 = − 2 a m e ⋅ d e d t = − 2 a m e ( − a m e − θ 2 ′ y + θ 1 ′ u c ) \begin{align} S1 :& 引入误差\\ &e =y-y_m \longrightarrow y_m = y-e \\ S2 :& 对误差求导\\ &\frac{\rm de}{\rm dt} = \frac{\rm dy}{\rm dt}-\frac{\rm dy_m}{\rm dt} \\ &= -ay+bu - (-a_my_m+b_mu_c) \\ &= -ay+b(\theta_1 u_c -\theta_2 y)+a_m(y-e)-b_mu_c \\ &=-a_me -(b\theta_2+a-a_m)y +b(\theta_1-b_m)u_c \\ S3 :& 简记 \left\{ \begin{array}{l} \theta_1' = b\theta_1-b_m \\ \theta_2' =b\theta_2+a-a_m \end{array} \right. ,有\frac{\rm de}{\rm dt}=-a_me -(b\theta_2')y +b(\theta_1')u_c \\ S4 :& 取能量函数\\ &V(e,\theta_1',\theta_2')=\frac{1}{2}\left[ e^2+\frac{1}{b \gamma}(\theta_2')^2+\frac{1}{b\gamma}(\theta_1')^2 \right] \\ S5 :& 对能量函数求导数 \\ &\frac{\rm dV}{\rm dt} = e\cdot \frac{\rm de}{\rm dt}+\frac{1}{b \gamma}\theta_2'\frac{\rm d\theta_2'}{dt}+\frac{1}{b \gamma}\theta_1'\frac{\rm d\theta_1'}{dt} \\ &= -a_me^2 +\theta_2'(\frac{\dot \theta_2'}{b\gamma}-ye) +\theta_1'(\frac{\dot \theta_1'}{b\gamma}+u_ce) \\ S6 :& 令 \left\{ \begin{array}{l} \frac{\dot \theta_2'}{b\gamma}-ye=0 \rightarrow \dot \theta_2'=b\gamma ye \\ \frac{\dot \theta_1'}{b\gamma}-u_ce=0 \rightarrow \dot \theta_1'=b\gamma u_ce \end{array} \right. \\ S7 :& \frac{\rm d^2V}{\rm dt^2} =-2a_me \cdot \frac{\rm de}{dt} \\ &=-2a_me(-a_me-\theta_2'y+\theta_1'u_c) \end{align} S1:S2:S3:S4:S5:S6:S7:引入误差e=y−ym⟶ym=y−e对误差求导dtde=dtdy−dtdym=−ay+bu−(−amym+bmuc)=−ay+b(θ1uc−θ2y)+am(y−e)−bmuc=−ame−(bθ2+a−am)y+b(θ1−bm)uc简记{θ1′=bθ1−bmθ2′=bθ2+a−am,有dtde=−ame−(bθ2′)y+b(θ1′)uc取能量函数V(e,θ1′,θ2′)=21[e2+bγ1(θ2′)2+bγ1(θ1′)2]对能量函数求导数dtdV=e⋅dtde+bγ1θ2′dtdθ2′+bγ1θ1′dtdθ1′=−ame2+θ2′(bγθ˙2′−ye)+θ1′(bγθ˙1′+uce)令{bγθ˙2′−ye=0→θ˙2′=bγyebγθ˙1′−uce=0→θ˙1′=bγucedt2d2V=−2ame⋅dtde=−2ame(−ame−θ2′y+θ1′uc) -
参数调整律与控制律形式如下:
d θ 1 d t = θ ˙ 1 ′ b = − γ u c e d θ 2 d t = θ ˙ 2 ′ b = − γ y e u ( t ) = − γ u c e s u c ( t ) − − γ y e s y ( t ) \frac{\rm d\theta_1}{\rm dt} = \frac{\dot \theta_1'}{b} = -\gamma u_ce \\ \frac{\rm d\theta_2}{\rm dt} = \frac{\dot \theta_2'}{b} = -\gamma ye \\ u(t) = \frac{-\gamma u_ce}{s}u_c(t)-\frac{-\gamma ye}{s}y(t) dtdθ1=bθ˙1′=−γucedtdθ2=bθ˙2′=−γyeu(t)=s−γuceuc(t)−s−γyey(t) -
Figure:
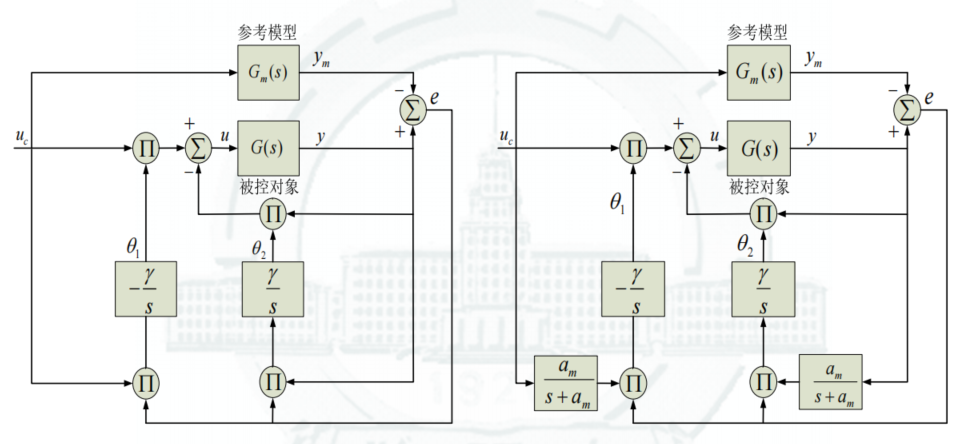
-
-
例2
-
以状态空间形式描述的系统:
d x m d t = A m x m + B m u c d x d t = A x + B u \frac{\rm dx_m}{\rm dt}=A_mx_m+B_mu_c \\ \frac{\rm dx}{\rm dt} =Ax+Bu dtdxm=Amxm+Bmucdtdx=Ax+Bu -
选择控制律的形式:
u = M u c − L x u=Mu_c-Lx u=Muc−Lx -
设计过程:
S 1 : 闭环系统化为 d x d t = A x + B ( M u c − L x ) = ( A − B L ) x + B M u c = d x d t = A c ( θ ) x + B c ( θ ) u c S 2 : 假设 A c ( θ ) , B c ( θ ) 满足 { A c ( θ 0 ) = A m B c ( θ 0 ) = B m S 3 : 假设以下方程有解 { A − B L = A m B M = B m S 4 : 因此 ( A − A m ) 的列和 B m 的列是 B 的列的线性组合,那么 { L = ( B T B ) − 1 B T ( A − A m ) = ( B m T B ) − 1 B m T ( A − A m ) M = ( B T B ) − 1 B T B m = ( B m T B ) − 1 B m T B m S 5 : 引入误差变量 e = x − x m ⟶ x m = x − e S 6 : 对误差变量求导 d e d t = d x d t − d x m d t = ( A − B L ) x + B M u c − A m x m − B m u c = A m e + ( A − B L − A m ) x + ( B M − B m ) u c = A m e + ( A c ( θ ) − A m ) x + ( B c ( θ ) − B m ) u c = A m e + Ψ ( θ − θ 0 ) S 7 : 选择能量函数 V ( e , θ ) = 1 2 [ γ e T P e + ( θ − θ 0 ) T ( θ − θ 0 ) ] S 8 : 对能量函数求导 d V d t = − γ 2 e T Q e + ( θ − θ 0 ) T ( d θ d t + γ Ψ T P e ) S 9 : 令 d θ d t + γ Ψ T P e = 0 ,有 d θ d t = − γ Ψ T P e \begin{align} S1 :& 闭环系统化为 \\ &\frac{\rm dx}{\rm dt} = Ax+B(Mu_c-Lx) = (A-BL)x+BMu_c = \frac{\rm dx}{\rm dt}=A_c(\theta)x+B_c(\theta)u_c\\ S2 :& 假设 A_c(\theta),B_c(\theta)满足 \left\{ \begin{array}{l} A_c(\theta^0)=A_m \\ B_c(\theta^0)=B_m \end{array} \right. \\ S3 :& 假设以下方程有解 \left\{ \begin{array}{l} A-BL = A_m \\ BM = B_m \end{array} \right. \\ S4 :& 因此(A-A_m)的列和B_m的列是B的列的线性组合,那么 \\ &\left\{ \begin{array}{l} L = (B^TB)^{-1}B^T(A-A_m) = (B_m^TB)^{-1}B_m^T(A-A_m) \\ M = (B^TB)^{-1}B^TB_m = (B_m^TB)^{-1}B_m^TB_m \end{array} \right. \\ S5 :& 引入误差变量 \\ &e = x-x_m \longrightarrow x_m=x-e \\ S6 :& 对误差变量求导 \\ &\frac{\rm de}{\rm dt} =\frac{\rm dx}{\rm dt}-\frac{\rm dx_m}{\rm dt} \\ &= (A-BL)x+BMu_c-A_mx_m-B_mu_c \\ &= A_me+(A-BL-A_m)x+(BM-B_m)u_c \\ &= A_me+(A_c(\theta)-A_m)x+(B_c(\theta)-B_m)u_c \\ &= A_me+\Psi(\theta-\theta^0) \\ S7 :& 选择能量函数 V(e,\theta)=\frac{1}{2}\left[ \gamma e^TPe+(\theta-\theta^0)^T(\theta-\theta^0) \right] \\ S8 :& 对能量函数求导 \frac{\rm dV}{\rm dt}=-\frac{\gamma}{2}e^TQe+(\theta-\theta^0)^T(\frac{\rm d\theta}{\rm dt}+\gamma\Psi^TPe) \\ S9 :& 令 \frac{\rm d\theta}{\rm dt} +\gamma\Psi^TPe =0 ,有 \frac{\rm d\theta}{\rm dt} = -\gamma\Psi^TPe \end{align} S1:S2:S3:S4:S5:S6:S7:S8:S9:闭环系统化为dtdx=Ax+B(Muc−Lx)=(A−BL)x+BMuc=dtdx=Ac(θ)x+Bc(θ)uc假设Ac(θ),Bc(θ)满足{Ac(θ0)=AmBc(θ0)=Bm假设以下方程有解{A−BL=AmBM=Bm因此(A−Am)的列和Bm的列是B的列的线性组合,那么{L=(BTB)−1BT(A−Am)=(BmTB)−1BmT(A−Am)M=(BTB)−1BTBm=(BmTB)−1BmTBm引入误差变量e=x−xm⟶xm=x−e对误差变量求导dtde=dtdx−dtdxm=(A−BL)x+BMuc−Amxm−Bmuc=Ame+(A−BL−Am)x+(BM−Bm)uc=Ame+(Ac(θ)−Am)x+(Bc(θ)−Bm)uc=Ame+Ψ(θ−θ0)选择能量函数V(e,θ)=21[γeTPe+(θ−θ0)T(θ−θ0)]对能量函数求导dtdV=−2γeTQe+(θ−θ0)T(dtdθ+γΨTPe)令dtdθ+γΨTPe=0,有dtdθ=−γΨTPe -
该方法要求系统中所有的状态变量都能被测量到。
-
-
例3
-
Figure:
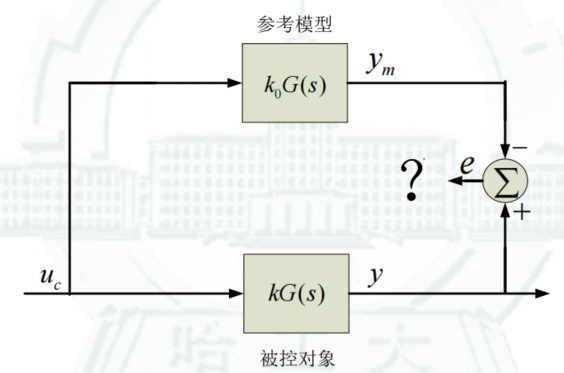
-
推导过程:
S 1 : 误差函数为 e = ( k G ( s ) θ − k 0 G ( s ) ) u c = k G ( s ) ( θ − θ 0 ) u c ,其中 θ 0 = k 0 k S 2 : 在状态空间中,参数 θ 和误差 e 之间的关系可以表示为 { d x d t = A x + B ( θ − θ 0 ) u c e = C x S 3 : 如果均质系统 x ˙ = A x 是渐进稳定的(传递函数严格正实, S P R ),存在正定矩阵 P 和 Q A T P + P A = − Q S 4 : 选择如下李雅普诺夫函数 V ( x , θ ) = 1 2 [ γ x T P x + ( θ − θ 0 ) 2 ] S 5 : 其导数为 d V d t = γ 2 ( d x T d t P x + x T P d x d t ) + ( θ − θ 0 ) d θ d t = γ 2 { [ A x + B u v ( θ − θ 0 ) ] T P x + x T P [ A x + B u c ( θ − θ 0 ) ] } + ( θ − θ 0 ) d θ d t = − γ 2 x T Q x + ( θ − θ 0 ) ( d θ d t + γ u c B T P x ) \begin{align} S1 :& 误差函数为 \\ & e=(kG(s)\theta - k_0G(s))u_c = kG(s)(\theta-\theta^0)u_c ,其中\theta^0=\frac{k_0}{k} \\ S2 :& 在状态空间中,参数\theta 和 误差 e之间的关系可以表示为 \\ & \left\{\begin{array}{l} \frac{\rm dx}{\rm dt}=Ax+B(\theta-\theta^0)u_c \\ e=Cx \end{array}\right. \\ S3 :& 如果均质系统\dot x=Ax 是渐进稳定的(传递函数严格正实,SPR),存在正定矩阵P和Q \\ & A^TP+PA=-Q \\ S4 :& 选择如下李雅普诺夫函数 \\ & V(x,\theta)=\frac{1}{2}\left[ \gamma x^TPx+(\theta-\theta^0)^2 \right] \\ S5 :& 其导数为 \\ & \frac{\rm dV}{\rm dt} = \frac{\gamma}{2}\left( \frac{\rm dx^T}{\rm dt}Px+x^TP\frac{\rm dx}{dt} \right) + (\theta-\theta^0)\frac{\rm d\theta}{\rm dt} \\ & =\frac{\gamma}{2}\left\{\left[Ax+Bu_v(\theta-\theta^0) \right]^TPx +x^TP\left[Ax+Bu_c(\theta-\theta^0) \right]\right\} + (\theta-\theta^0)\frac{\rm d\theta}{\rm dt} \\ & =-\frac{\gamma}{2}x^TQx+(\theta-\theta^0)(\frac{\rm d\theta}{\rm dt}+\gamma u_cB^TPx) \end{align} S1:S2:S3:S4:S5:误差函数为e=(kG(s)θ−k0G(s))uc=kG(s)(θ−θ0)uc,其中θ0=kk0在状态空间中,参数θ和误差e之间的关系可以表示为{dtdx=Ax+B(θ−θ0)uce=Cx如果均质系统x˙=Ax是渐进稳定的(传递函数严格正实,SPR),存在正定矩阵P和QATP+PA=−Q选择如下李雅普诺夫函数V(x,θ)=21[γxTPx+(θ−θ0)2]其导数为dtdV=2γ(dtdxTPx+xTPdtdx)+(θ−θ0)dtdθ=2γ{[Ax+Buv(θ−θ0)]TPx+xTP[Ax+Buc(θ−θ0)]}+(θ−θ0)dtdθ=−2γxTQx+(θ−θ0)(dtdθ+γucBTPx) -
如果选择参数调整律为:
d θ d t = − γ u c B T P x \frac{\rm d\theta}{\rm dt}=-\gamma u_cB^TPx dtdθ=−γucBTPx
此时,在 x ≠ 0 x \neq 0 x=0 的情况下, d V / d t < 0 \rm dV /\rm dt <0 dV/dt<0 成立;当 t → ∞ t \rightarrow \infin t→∞ 时,状态向量 x → 0 x \rightarrow 0 x→0 且误差 e = C x → 0 e=Cx \rightarrow0 e=Cx→0 ;但是不能保证参数误差 θ − θ 0 \theta-\theta^0 θ−θ0 趋于 0 0 0。 -
输出反馈
-
存在的问题:上述结果是非常严格的,因为它要求全部状态可测。
-
假设传递函数严格正实(SPR),存在正定矩阵 P , Q P,Q P,Q ,使得:
A T P + P A = − Q A^TP+PA=-Q ATP+PA=−Q -
如果李雅普诺夫方程可以选择,就可以得到一个利用输出反馈的参数调整律,令:
B T P = C B^TP=C BTP=C
其中, C C C 是系统的输出矩阵。选定此 P P P 后,有:
B T P x = C x = e B^TPx=Cx=e BTPx=Cx=e
于是参数调整律变化为:
d θ d t = − γ u c B T P x = − γ u c C x = − γ u c e \frac{\rm d\theta}{\rm dt} = -\gamma u_c B^TPx = -\gamma u_c Cx = -\gamma u_c e dtdθ=−γucBTPx=−γucCx=−γuce
-
-
MIT 方案: d θ d t = − γ ⋅ e ⋅ y m \frac{\rm d\theta}{\rm dt}=- \gamma \cdot e \cdot y_m dtdθ=−γ⋅e⋅ym
基于Lyapunov稳定性理论的结果: d θ d t = − γ u c e \frac{\rm d\theta}{\rm dt}=-\gamma u_c e dtdθ=−γuce
-
Figure:
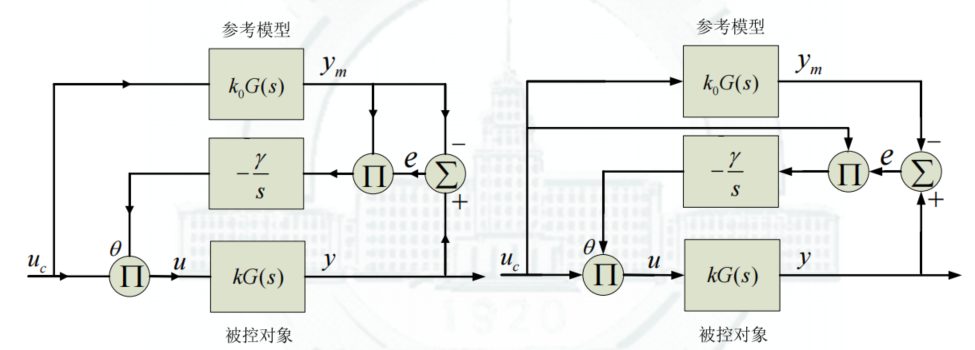
-
15-增益调度自适应系统
一、增益调度系统概述
-
Figure:
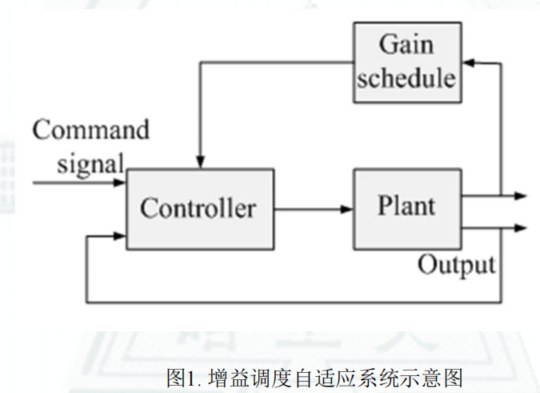
-
思想:利用辅助变量测出环境或者被控对象自身的变化,比如“增益”的变化,然后利用控制器补偿这种“增益”的变化所引起的控制系统性能的降低。
-
实现:通过“函数设定”或“查表法”,又称为增益列表补偿法。
二、增益调度自适应控制系统举例
-
例1:非线性阀门控制系统
-
Figure:非线性阀门控制系统框图
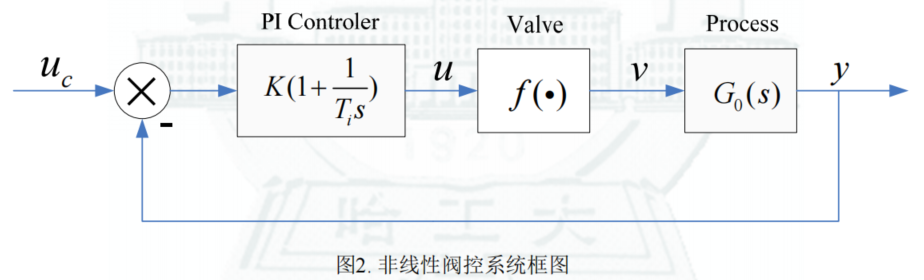
假设系统存在非线性环节 f ( ⋅ ) f(\cdot) f(⋅),系统参数:
G 0 ( s ) = 1 ( s + 1 ) 3 ν = f ( u ) = u 4 , u ≥ 0 G c ( s ) = K [ 1 + 1 T i s ] T i = 1 , K = 0.15 \begin{matrix} G_0(s)=\frac{1}{(s+1)^3} & \nu=f(u)=u^4,u\geq 0 \\ G_c(s)=K\left[ 1+\frac{1}{T_is} \right] & T_i=1,K=0.15 \end{matrix} G0(s)=(s+1)31Gc(s)=K[1+Tis1]ν=f(u)=u4,u≥0Ti=1,K=0.15
u c u_c uc 为阶跃信号,当其增大后,系统振荡。 -
Figure:加上非线性环节后的控制系统的框图
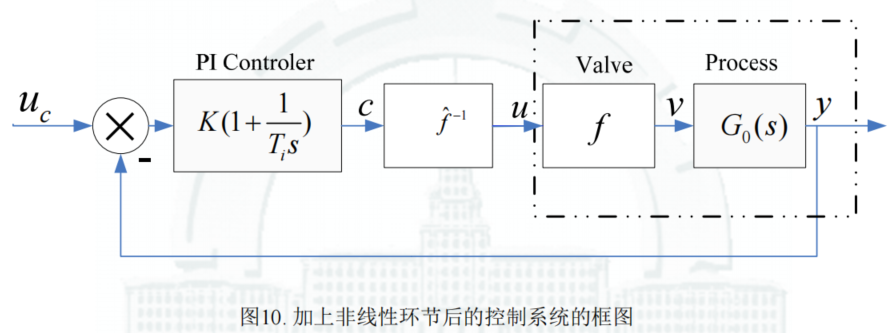
对非线性环节的逆的估计:
f ^ − 1 ( c ) = { 0.433 c , 0 ≤ c ≤ 3 0.0538 c + 1.139 , 3 ≤ c ≤ 16 \hat f^{-1}(c)= \left\{ \begin{align} &0.433c, &0 \leq c \leq 3 \\ &0.0538c+1.139, &3 \leq c \leq 16 \end{align} \right. f^−1(c)={0.433c,0.0538c+1.139,0≤c≤33≤c≤16
加入非线性环节后,系统特性变好,当 u c u_c uc 较大时,系统也不再振荡。 -
阀门的输入作为调度变量,改变“开环增益”来补偿阀门非线性特性对系统造成的影响。
-
总结:通过增加非线性补偿环节,闭环系统的特性有显著提高。可以通过改进补偿环节的近似程度进一步提高闭环系统的性能。
-
问题:阀门的非线性特性要是不知道呢?
-
-
例2:水位控制系统
-
Figure:水位控制系统框图
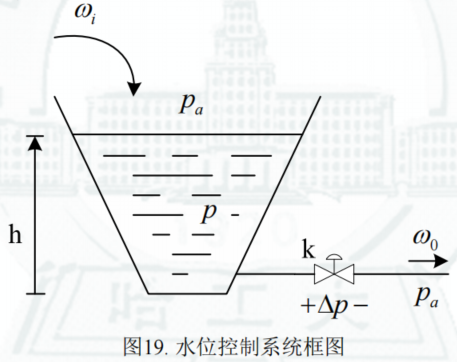
其中:
A ( h ) ——水箱的横截面积, h ——液位的高度, ρ ——液体的密度, p = ρ g h + p a ——液体内部的压强,其中 p a 为标准大气压强(假设为常数) ω i ——输入流量, ω o = k Δ p ——输出流量,其中 Δ p = p − p a 。 \begin{align} A(h) &——水箱的横截面积, \\ h &——液位的高度, \\ \rho &——液体的密度, \\ p=\rho g h +p_a &——液体内部的压强,其中p_a为标准大气压强(假设为常数) \\ \omega_i &——输入流量, \\ \omega_o=k \sqrt{\Delta p} &——输出流量,其中\Delta p=p-p_a。 \\ \end{align} A(h)hρp=ρgh+paωiωo=kΔp——水箱的横截面积,——液位的高度,——液体的密度,——液体内部的压强,其中pa为标准大气压强(假设为常数)——输入流量,——输出流量,其中Δp=p−pa。 -
体积的表示:
V = ∫ 0 h A ( τ ) d τ d V d t = A ( h ) d h d t = ω i − k ρ g h V=\int ^h_0A(\tau)\rm d\tau \\ \frac{\rm dV}{\rm dt} =A(h) \frac{\rm dh}{\rm dt} =\omega_i -k \sqrt{\rho g h} V=∫0hA(τ)dτdtdV=A(h)dtdh=ωi−kρgh -
推导过程
-
系统的状态空间描述:
x ˙ = 1 A ( x ) ( u − c x ) = f ( x , u ) y = x \begin{align} \dot x&=\frac{1}{A(x)}(u-c\sqrt{x})=f(x,u) \\ y&=x \end{align} x˙y=A(x)1(u−cx)=f(x,u)=x
其中: x = h , u = ω i , c = k ρ g x=h,u=\omega_i,c=k\sqrt{\rho g} x=h,u=ωi,c=kρg 。 -
引入增广系统:
{ x ˙ = f ( x , u ) σ ˙ = x − r y = x \left\{ \begin{array}{l} \dot x=f(x,u) \\ \dot \sigma =x-r \end{array} \right. \\ y=x {x˙=f(x,u)σ˙=x−ry=x
引入比例积分控制律:
u = − k 1 ( α ) e − k 2 ( α ) σ u=-k_1(\alpha)e-k_2(\alpha)\sigma u=−k1(α)e−k2(α)σ
其中, α \alpha α 为期望的水位高度。有:
x ˙ = 1 A ( x ) [ − k 1 ( α ) e − k 2 ( α ) σ − c x ] \dot x =\frac{1}{A(x)}\left[-k_1(\alpha)e-k_2(\alpha) \sigma -c\sqrt{x}\right] x˙=A(x)1[−k1(α)e−k2(α)σ−cx] -
以上系统在平衡点 ( x s s , σ s s ) (x_{ss},\sigma_{ss}) (xss,σss) 处线性化后得到:
[ x ˙ δ σ ˙ δ ] = [ − c ( α ) 2 A ( α ) α − 1 A ( α ) k 1 ( α ) − 1 A ( α ) k 2 ( α ) 1 0 ] [ x δ σ δ ] + [ 1 A ( α ) k 1 ( α ) − 1 ] r δ y δ = [ 1 0 ] [ x δ σ δ ] \begin{align} \left[\begin{matrix} \dot x_\delta \\ \dot \sigma_\delta \end{matrix}\right] &= \left[\begin{matrix} -\frac{c\sqrt(\alpha)}{2A(\alpha)\alpha}-\frac{1}{A(\alpha)}k_1(\alpha) & -\frac{1}{A(\alpha)}k_2(\alpha) \\ 1 & 0 \end{matrix}\right] \left[\begin{matrix} x_\delta \\ \sigma_\delta \end{matrix}\right] + \left[\begin{matrix} \frac{1}{A(\alpha)}k_1(\alpha) \\ -1 \end{matrix}\right] r_\delta \\ y_\delta &= \left[\begin{matrix} 1 & 0 \end{matrix}\right] \left[\begin{matrix} x_\delta \\ \sigma_\delta \end{matrix}\right] \end{align} [x˙δσ˙δ]yδ=[−2A(α)αc(α)−A(α)1k1(α)1−A(α)1k2(α)0][xδσδ]+[A(α)1k1(α)−1]rδ=[10][xδσδ]
简记为:
ξ ˙ δ = [ a ( α ) − b ( α ) k 1 ( α ) − b ( α ) k 2 ( α ) 1 0 ] ξ δ + [ b ( α ) k 1 ( α ) − 1 ] r δ y δ = [ 1 0 ] [ x δ σ δ ] \begin{align} \dot \xi_\delta &=\left[ \begin{matrix} a(\alpha)-b(\alpha)k_1(\alpha) & -b(\alpha)k_2(\alpha) \\ 1 & 0 \end{matrix} \right] \xi_\delta +\left[ \begin{matrix} b(\alpha)k_1(\alpha) \\ -1 \end{matrix} \right]r_\delta \\ y_\delta &= \left[\begin{matrix} 1 & 0 \end{matrix}\right] \left[\begin{matrix} x_\delta \\ \sigma_\delta \end{matrix}\right] \end{align} ξ˙δyδ=[a(α)−b(α)k1(α)1−b(α)k2(α)0]ξδ+[b(α)k1(α)−1]rδ=[10][xδσδ]
其中:
b ( α ) = 1 A ( α ) a ( α ) = − c α 2 A ( α ) α ξ δ = [ x δ σ δ ] T x δ = x − α σ δ = σ − σ s s r δ = r − α \begin{matrix} b(\alpha) = \frac{1}{A(\alpha)} & a(\alpha)=-\frac{c\sqrt{\alpha}}{2A(\alpha)\alpha} \\ \xi_\delta = \left[ \begin{matrix} x_\delta & \sigma_\delta \end{matrix} \right]^T & x_\delta=x-\alpha \\ \sigma_\delta=\sigma-\sigma_{ss} & r_\delta =r-\alpha \end{matrix} b(α)=A(α)1ξδ=[xδσδ]Tσδ=σ−σssa(α)=−2A(α)αcαxδ=x−αrδ=r−α -
选取控制器参数:
k 1 ( α ) = A ( α ) 2 ξ ω n k 2 ( α ) = A ( α ) ω n 2 \begin{align} k_1(\alpha) &= A(\alpha)2\xi\omega_n \\ k_2(\alpha) &= A(\alpha)\omega_n^2 \end{align} k1(α)k2(α)=A(α)2ξωn=A(α)ωn2
闭环系统方程:
ξ ˙ δ = [ a ( α ) − 2 ξ ω n − ω n 2 1 0 ] ξ δ + [ 2 ξ ω n − 1 ] r δ y δ = [ 1 0 ] ξ δ \begin{align} \dot \xi_\delta &= \left[ \begin{matrix} a(\alpha)-2\xi\omega_n & -\omega_n^2 \\ 1 & 0 \end{matrix} \right] \xi_\delta + \left[ \begin{matrix} 2\xi\omega_n \\ -1 \end{matrix} \right] r_\delta \\ y_\delta &= \left[ \begin{matrix} 1 & 0 \end{matrix} \right] \xi_\delta \end{align} ξ˙δyδ=[a(α)−2ξωn1−ωn20]ξδ+[2ξωn−1]rδ=[10]ξδ
被控对象的传递函数:
G ( s ) = 2 ξ ω n s + ω n 2 s 2 + [ 2 ξ ω n − a ( α ) ] s + ω n 2 G(s) = \frac{2\xi\omega_n s+\omega_n^2}{s^2+[2\xi\omega_n-a(\alpha)]s+\omega_n^2} G(s)=s2+[2ξωn−a(α)]s+ωn22ξωns+ωn2 -
此时,控制律的形式:
u = − k 1 ( α ) e − k 2 ( α ) σ σ ˙ = x − r \begin{align} u &=-k_1(\alpha)e-k_2(\alpha)\sigma \\ \dot \sigma &=x-r \end{align} uσ˙=−k1(α)e−k2(α)σ=x−r
增益调度控制律:
u = − k 1 ( r ) e − k 2 ( r ) σ σ ˙ = x − r \begin{align} u &=-k_1(r)e-k_2(r)\sigma \\ \dot \sigma &=x-r \end{align} uσ˙=−k1(r)e−k2(r)σ=x−r -
引入增益调度控制器后,闭环系统变为:
{ x ˙ = f [ x , − k 1 ( r ) ( x − r ) − k 2 ( r ) σ ] σ ˙ = x − r y = x \begin{align} &\left\{ \begin{matrix} \dot x=f\left[x,-k_1(r)(x-r)-k_2(r)\sigma\right] \\ \dot \sigma =x-r \end{matrix} \right. \\ &y=x \end{align} {x˙=f[x,−k1(r)(x−r)−k2(r)σ]σ˙=x−ry=x
其中
x ˙ = 1 A ( x ) [ − k 1 ( r ) ( x − r ) − k 2 ( r ) σ − c x ] \dot x =\frac{1}{A(x)}\left[-k_1(r)(x-r)-k_2(r)\sigma-c\sqrt{x}\right] x˙=A(x)1[−k1(r)(x−r)−k2(r)σ−cx] -
此时被控对象的传递函数:
G ( s ) = [ 2 ξ ω n + γ ( α ) ] s + ω n 2 s 2 + [ 2 ξ ω n − a ( α ) ] s + ω n 2 G(s)= \frac{[2\xi\omega_n+\gamma(\alpha)]s+\omega_n^2}{s^2+[2\xi\omega_n-a(\alpha)]s+\omega_n^2} G(s)=s2+[2ξωn−a(α)]s+ωn2[2ξωn+γ(α)]s+ωn2
其中:
γ ( α ) = A ′ ( α ) c α A 2 ( α ) \gamma(\alpha) = \frac{A'(\alpha)c\sqrt{\alpha}}{A^2(\alpha)} γ(α)=A2(α)A′(α)cα -
修改后的控制算法:
u = − k 1 ( r ) e − k 2 ( r ) σ σ ˙ = x − r ⟶ u = − k 1 ( r ) e + η η ˙ = − k 2 ( r ) e \begin{array}{l} u=-k_1(r)e-k_2(r)\sigma \\ \dot \sigma =x-r \end{array} \longrightarrow \begin{array}{l} u=-k_1(r)e+\eta \\ \dot \eta =-k_2(r)e \end{array} u=−k1(r)e−k2(r)σσ˙=x−r⟶u=−k1(r)e+ηη˙=−k2(r)e
-
-
Figure:原始增益调度算法与修改后的增益调度算法
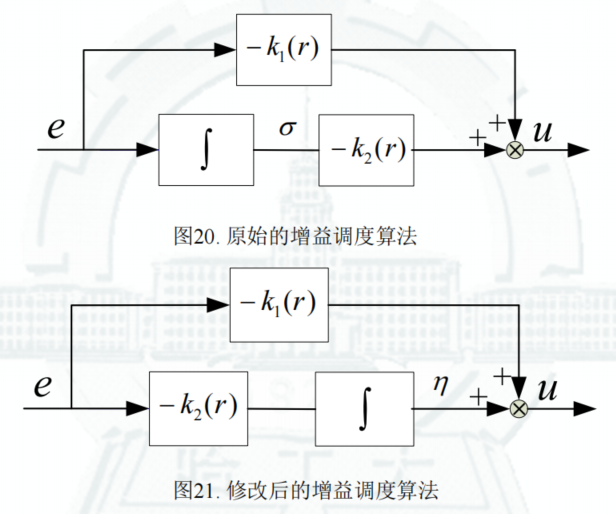
根据修改后的控制算法,闭环系统在平衡点线性化:
ξ ˙ δ = [ a ( α ) − 2 ξ ω n b ( α ) − ω n 2 b ( α ) 0 ] ξ δ + [ 2 ξ ω ω n 2 b ( α ) ] r δ y δ = [ 1 0 ] ξ δ \begin{align} \dot \xi_\delta &= \left[\begin{matrix} a(\alpha)-2\xi\omega_n & b(\alpha) \\ -\frac{\omega_n^2}{b(\alpha)} & 0 \end{matrix}\right] \xi_\delta+ \left[\begin{matrix} 2\xi\omega \\ \frac{\omega_n^2}{b(\alpha)} \end{matrix}\right] r_\delta \\ y_\delta &=\left[\begin{matrix} 1 & 0 \end{matrix}\right] \xi_\delta \end{align} ξ˙δyδ=[a(α)−2ξωn−b(α)ωn2b(α)0]ξδ+[2ξωb(α)ωn2]rδ=[10]ξδ
平衡点的传递函数:
G ( s ) = 2 ξ ω n s + ω n 2 s 2 + [ 2 ξ ω − a ( α ) ] s + ω n 2 G(s)=\frac{2\xi\omega_ns+\omega_n^2}{s^2+[2\xi\omega-a(\alpha)]s+\omega_n^2} G(s)=s2+[2ξω−a(α)]s+ωn22ξωns+ωn2 -
Figure:开环对象
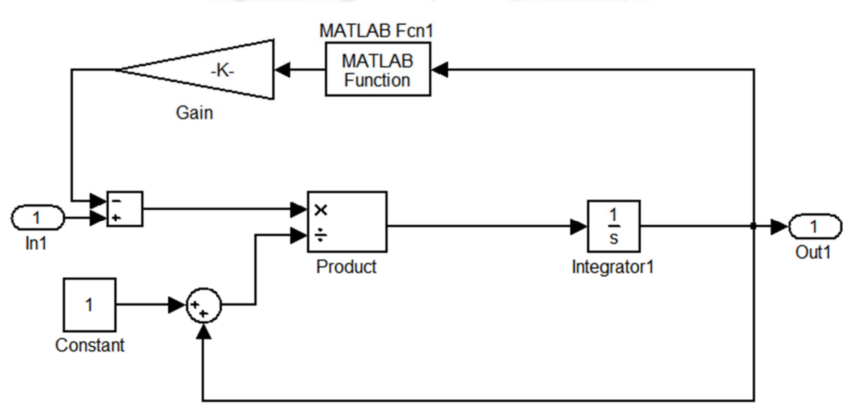
-
Figure:定系数 PI 控制律仿真图
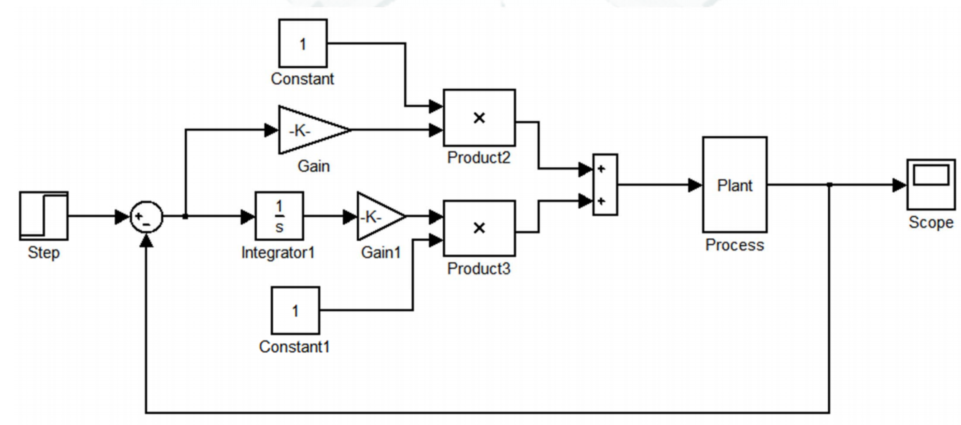
当阶跃信号 r r r 很大时,系统会发生振荡。
-
Figure:增益调度系统仿真框图
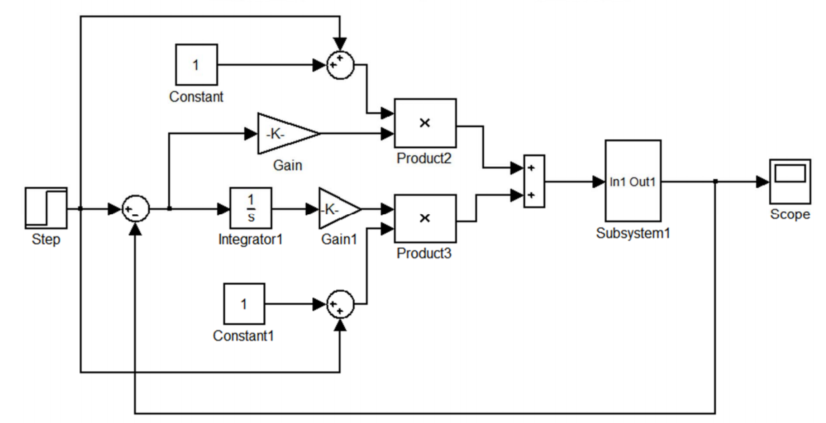
当阶跃信号 r r r 很大时,系统也不会发生振荡。
-
-
例3:考虑如下非线性系统
-
系统的表示:
x ˙ = f ( x , u , ν , ω ) y = h ( x , ω ) y m = h m ( x , ω ) \begin{align} \dot x &= f(x,u,\nu,\omega) \\ y &= h(x,\omega) \\ y_m &= h_m(x,\omega) \end{align} x˙yym=f(x,u,ν,ω)=h(x,ω)=hm(x,ω)
其中:
x ——状态变量; u ——控制输入; ν ——可测到的外部输入; ω ——不确知的常参数; y ——被控输出; y m ——能测量到的有关系统的信息。 \begin{align} x &——状态变量;\\ u &——控制输入;\\ \nu &——可测到的外部输入;\\ \omega &——不确知的常参数;\\ y &——被控输出;\\ y_m &——能测量到的有关系统的信息。 \end{align} xuνωyym——状态变量;——控制输入;——可测到的外部输入;——不确知的常参数;——被控输出;——能测量到的有关系统的信息。 -
目的:设计“输出”反馈控制律,使系统能够“很好的”跟踪指令信号 r r r 。
具体来说,就是考虑存在不确定性 ω \omega ω 的条件下,利用能够测量到的量(调度变量) ρ = [ r ν ] \rho=\left[ \begin{matrix} r \\ \nu \end{matrix} \right] ρ=[rν],最终使得控制偏差在给定范围或者趋于零,即 e = y − r → 0 e=y-r \rightarrow 0 e=y−r→0 。
-
以 ρ \rho ρ 作为调度变量, ρ = α \rho=\alpha ρ=α ,控制律形式如下:
σ ˙ = e = y − r (为了消除稳态误差引入的项) z ˙ = F ( α ) z + G 1 ( α ) σ + G 2 ( α ) y m u = L ( α ) z + M 1 ( α ) σ + M 2 ( α ) y m + M 3 ( α ) e \begin{array}{l} \dot \sigma =e=y-r(为了消除稳态误差引入的项) \\ \dot z=F(\alpha)z+G_1(\alpha)\sigma+G_2(\alpha)y_m \\ u=L(\alpha)z+M_1(\alpha)\sigma+M_2(\alpha)y_m+M_3(\alpha)e \end{array} σ˙=e=y−r(为了消除稳态误差引入的项)z˙=F(α)z+G1(α)σ+G2(α)ymu=L(α)z+M1(α)σ+M2(α)ym+M3(α)e
闭环系统方程如下:
x ˙ = f ( x , L ( α ) z + M 1 ( α ) σ + M 2 ( α ) h m ( x , ω ) + M 3 ( α ) e , ν , ω ) σ ˙ = e = h ( x , ω ) − r z ˙ = F ( α ) z + G 1 ( α ) σ + G 2 ( α ) h m ( x , ω ) y = h ( x , ω ) \begin{array}{l} \dot x=f(x,L(\alpha)z+M_1(\alpha)\sigma+M_2(\alpha)h_m(x,\omega)+M_3(\alpha)e,\nu,\omega) \\ \dot \sigma=e=h(x,\omega)-r \\ \dot z=F(\alpha)z+G_1(\alpha)\sigma+G_2(\alpha)h_m(x,\omega) \\ y=h(x,\omega) \end{array} x˙=f(x,L(α)z+M1(α)σ+M2(α)hm(x,ω)+M3(α)e,ν,ω)σ˙=e=h(x,ω)−rz˙=F(α)z+G1(α)σ+G2(α)hm(x,ω)y=h(x,ω)在平衡点 ( x , σ , z ) = ( x s s , σ s s , z s s ) (x,\sigma,z)=(x_{ss},\sigma_{ss},z_{ss}) (x,σ,z)=(xss,σss,zss) 以及 ρ = α \rho=\alpha ρ=α 处线性化处理得:
{ ξ ˙ δ = A f ( α , ω ) ξ δ + B f ( α , ω ) ρ δ y δ = C f ( α , ω ) ξ δ A f = [ A + B M 2 C m + B M 3 C B M 1 B L C 0 0 G 2 C m G 1 F ] B f = [ − B M 3 E − I 0 0 0 ] C f = [ C 0 0 ] \left\{\begin{array}{l} \dot \xi_\delta = A_f(\alpha,\omega)\xi_\delta+B_f(\alpha,\omega)\rho_\delta \\ y_\delta=C_f(\alpha,\omega)\xi_\delta \end{array}\right. \\ \begin{matrix} A_f = \left[ \begin{matrix} A+BM_2C_m+BM_3C & BM_1 & BL \\ C & 0 & 0 \\ G_2C_m & G_1 & F \end{matrix} \right] & B_f=\left[ \begin{matrix} -BM_3 & E \\ -I & 0 \\ 0 & 0 \end{matrix} \right] \\ C_f=\left[ \begin{matrix} C & 0 & 0 \end{matrix} \right] \end{matrix} {ξ˙δ=Af(α,ω)ξδ+Bf(α,ω)ρδyδ=Cf(α,ω)ξδAf= A+BM2Cm+BM3CCG2CmBM10G1BL0F Cf=[C00]Bf= −BM3−I0E00
其中:
A = ∂ f ∂ x B = ∂ f ∂ u C = ∂ h ∂ x C m = ∂ h m ∂ x E = ∂ f ∂ ν ξ δ = [ x − x s s σ − σ s s z − z s s ] ρ s s = ρ − α = [ r δ ν δ ] \begin{matrix} A=\frac{\partial f}{\partial x} & B=\frac{\partial f}{\partial u} & C=\frac{\partial h}{\partial x} & C_m=\frac{\partial h_m}{\partial x} \\ E=\frac{\partial f}{\partial \nu} & \xi_\delta=\left[\begin{matrix}x-x_{ss}\\\sigma-\sigma_{ss}\\z-z_{ss}\end{matrix}\right] & \rho_{ss}=\rho-\alpha=\left[\begin{matrix}r_\delta\\\nu_\delta\end{matrix}\right] \end{matrix} A=∂x∂fE=∂ν∂fB=∂u∂fξδ= x−xssσ−σssz−zss C=∂x∂hρss=ρ−α=[rδνδ]Cm=∂x∂hm
最终的增益调度控制律:
σ ˙ = e = y − r z ˙ = F ( ρ ) z + G 1 ( ρ ) σ + G 2 ( ρ ) y m ( F ( ρ ) 将固定的“值”用调度变量代替) u = L ( ρ ) z + M 1 ( ρ ) σ + M 2 ( ρ ) y m + M 3 ( ρ ) e \begin{array}{l} \dot \sigma = e =y-r \\ \dot z =F(\rho) z+G_1(\rho)\sigma +G_2(\rho)y_m (F(\rho)将固定的“值”用调度变量代替)\\ u=L(\rho)z+M_1(\rho)\sigma+M_2(\rho)y_m+M_3(\rho)e \end{array} σ˙=e=y−rz˙=F(ρ)z+G1(ρ)σ+G2(ρ)ym(F(ρ)将固定的“值”用调度变量代替)u=L(ρ)z+M1(ρ)σ+M2(ρ)ym+M3(ρ)e -
修改控制律,假设可以测量到 y ˙ m \dot y_m y˙m :
φ ˙ = F ( ρ ) φ + G 1 ( ρ ) e + G 2 ( ρ ) y ˙ m η ˙ = L ( ρ ) φ + M 1 ( ρ ) e + M 2 ( ρ ) y ˙ m u = η + M 3 ( ρ ) e \begin{array}{l} \dot \varphi=F(\rho)\varphi +G_1(\rho)e +G_2(\rho)\dot y_m \\ \dot \eta =L(\rho)\varphi +M_1(\rho)e +M_2(\rho)\dot y_m \\ u =\eta +M_3(\rho)e \end{array} φ˙=F(ρ)φ+G1(ρ)e+G2(ρ)y˙mη˙=L(ρ)φ+M1(ρ)e+M2(ρ)y˙mu=η+M3(ρ)e
整个闭环系统变为:
x ˙ = f ( x , η + M 3 ( ρ ) e , ν , ω ) φ ˙ = F ( ρ ) φ + G 1 ( ρ ) e + G 2 ( ρ ) y ˙ m η ˙ = L ( ρ ) φ + M 1 ( ρ ) e + M 2 ( ρ ) y ˙ m \begin{array}{l} \dot x=f(x,\eta+M_3(\rho)e,\nu,\omega) \\ \dot \varphi=F(\rho)\varphi +G_1(\rho)e +G_2(\rho)\dot y_m \\ \dot \eta =L(\rho)\varphi +M_1(\rho)e +M_2(\rho)\dot y_m \end{array} x˙=f(x,η+M3(ρ)e,ν,ω)φ˙=F(ρ)φ+G1(ρ)e+G2(ρ)y˙mη˙=L(ρ)φ+M1(ρ)e+M2(ρ)y˙m
其中:
{ y = h ( x , ω ) e = h ( e , ω ) − r y ˙ m = ∂ h m ∂ x ( x , ω ) f ( x , η + M 3 ( ρ ) e , ν , ω ) \left\{\begin{array}{l} y=h(x,\omega) \\ e=h(e,\omega)-r \\ \dot y_m = \frac{\partial h_m}{\partial x}(x,\omega)f(x,\eta+M_3(\rho)e,\nu,\omega) \end{array}\right. ⎩ ⎨ ⎧y=h(x,ω)e=h(e,ω)−ry˙m=∂x∂hm(x,ω)f(x,η+M3(ρ)e,ν,ω)
整个闭环系统的状态空间表达式简写如下:
X ˙ = g ( X , ρ , ω ) y = h ( x , ω ) \dot X=g(X,\rho,\omega) \\ y = h(x,\omega) \\ X˙=g(X,ρ,ω)y=h(x,ω)
其中:
X = [ x φ η ] g ( X , ρ , φ ) = [ f ( x , η + M 3 ( ρ ) e , ν , ω ) F ( ρ ) φ + G 1 ( ρ ) e + G 2 ( ρ ) y ˙ m L ( ρ ) φ + M 1 ( ρ ) e + M 2 ( ρ ) y ˙ m ] \begin{matrix} X=\left[\begin{matrix} x\\ \varphi\\ \eta \end{matrix}\right] & g(X,\rho,\varphi)=\left[\begin{matrix}f(x,\eta+M_3(\rho)e,\nu,\omega) \\ F(\rho)\varphi+G_1(\rho)e+G_2(\rho)\dot y_m \\ L(\rho)\varphi+M_1(\rho)e+M_2(\rho)\dot y_m \end{matrix}\right] \end{matrix} X= xφη g(X,ρ,φ)= f(x,η+M3(ρ)e,ν,ω)F(ρ)φ+G1(ρ)e+G2(ρ)y˙mL(ρ)φ+M1(ρ)e+M2(ρ)y˙m -
定理:考虑上述状态空间下的闭环系统,假设 ρ ( t ) \rho(t) ρ(t) 是连续可微的, ρ ( t ) ∈ S \rho(t) \in S ρ(t)∈S, S S S 是 D ρ D_\rho Dρ 的一个紧子集,并且 ∥ ρ ˙ ( t ) ∥ ≤ μ , ∀ t ≥ 0 \| \dot \rho(t) \| \leq \mu,\forall t \geq0 ∥ρ˙(t)∥≤μ,∀t≥0 。那么,存在正的常数 k 1 , k 2 , k 3 k_1,k_2,k_3 k1,k2,k3 和 T T T ,使得如果 μ < k 1 \mu < k_1 μ<k1 且 ∥ X ( 0 ) − X s s ( ρ ( 0 ) , ω ) ∥ ≤ k 2 \| X(0)-X_{ss}(\rho(0),\omega) \| \leq k_2 ∥X(0)−Xss(ρ(0),ω)∥≤k2 ,那么 X ( t ) X(t) X(t) 在 t ≥ 0 t \geq0 t≥0 上为一致有界,并且:
∥ e ( t ) ∥ ≤ k μ , ∀ t ≥ T \| e(t) \| \leq k\mu,\forall t \geq T ∥e(t)∥≤kμ,∀t≥T
更进一步,如果 ρ ( t ) → ρ s s \rho(t) \rightarrow \rho_{ss} ρ(t)→ρss 并且当 t → ∞ t \rightarrow \infin t→∞ 时 ρ ˙ ( t ) → 0 \dot \rho(t) \rightarrow 0 ρ˙(t)→0 ,那么:
e ( t ) → 0 , t → ∞ e(t) \rightarrow 0,t \rightarrow \infin e(t)→0,t→∞
定理说明:如果调度变量缓慢变化并且初始状态离平衡点足够的近,那么跟踪误差将会与调度变量的变化值成正比,并且如果调度变量趋近于常值,则跟踪误差将趋近于零。 -
假如得不到 y ˙ m \dot y_m y˙m,则采用如下控制律:
φ ˙ = F ( ρ ) φ + G 1 ( ρ ) e + G 2 ( ρ ) ϑ η ˙ = L ( ρ ) φ + M 1 ( ρ ) e + M 2 ( ρ ) ϑ u = η + M 3 ( ρ ) e ε ξ ˙ = − ξ + y m , ϑ = 1 ε ( − ξ + y m ) \begin{array}{l} \dot \varphi=F(\rho)\varphi+G_1(\rho)e+G_2(\rho) \vartheta \\ \dot \eta =L(\rho) \varphi +M_1(\rho)e +M_2(\rho)\vartheta \\ u =\eta +M_3(\rho)e \\ \varepsilon \dot \xi =-\xi+y_m,\vartheta=\frac{1}{\varepsilon}(-\xi+y_m) \end{array} φ˙=F(ρ)φ+G1(ρ)e+G2(ρ)ϑη˙=L(ρ)φ+M1(ρ)e+M2(ρ)ϑu=η+M3(ρ)eεξ˙=−ξ+ym,ϑ=ε1(−ξ+ym)
最终的闭环传递函数为:
X ˙ = g ( X , ρ , ω ) + N ( ρ ) ( ϑ − y ˙ m ) ε ϑ ˙ = − ϑ + y ˙ m y = h ( x , ω ) N ( ρ ) = [ 0 G 2 M 2 ] \begin{array}{l} \dot X=g(X,\rho,\omega)+N(\rho)(\vartheta-\dot y_m) \\ \varepsilon \dot \vartheta = -\vartheta +\dot y_m \\ y = h(x,\omega) \\ N(\rho) = \left[\begin{matrix} 0 \\ G_2 \\M_2 \end{matrix}\right] \end{array} X˙=g(X,ρ,ω)+N(ρ)(ϑ−y˙m)εϑ˙=−ϑ+y˙my=h(x,ω)N(ρ)= 0G2M2
-
-
例4:空间机器人重力补偿控制系统
-
结论:增益调度方法思路简洁,可有效提高非线性控制系统的控制性能。
-
问题:如何将增益调度的思路和基于参数估计的随机自适应系统有效结合?
将会与调度变量的变化值成正比,并且如果调度变量趋近于常值,则跟踪误差将趋近于零。






















 5027
5027











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








