2016.8.6 学习总结

KMP

　　首先是KMP。
　　KMP是一种字符串快速匹配的的方法。
　　核心思想就是：避免判断一些没必要判断的，省略了这些，就直接跳跃到有可能成功匹配的合法位置。
　　是不是经过我这番说辞就感觉KMP很高大上。其实这就是一种暴力的剪枝罢了。
　　
　　光说是没有什么卵用的，那么，我就来继续说说KMP的大概流程（也就是模板）吧。
　　
　　1.读入
　　2.定义并初始化一个叫做next的数组 *next
　　3.运用next数组来暴力匹配字符串
　　　　a.匹配成功时，自然不用说，继续匹配下去就好了
　　　　b.当匹配失败时，就不是像普通无脑的暴力做法一样，把指针指向第一个，继续从i+1个开始匹配了。而是通过next数组，把指针指向next[i]，从这个位置开始匹配。因为即使当前不成功，next位置的也是有可能成功的。这就会省去很多的时间，大大减少了时间复杂度。
　　　　c.当匹配完成时，也还是把指针跳到next[i]（如果你说不能重叠，那就跳到第一个lor）。顺便把答案+1。
　　4.输出
　　
　　什么？你说不相信时间复杂度会减少？那就举个栗子，用栗子说话【栗子怎么会说话，这人有问题
　　
　　现在要求S字符串中，T字符串出现多少次。
　　当 S=”aaaaaab”且 T=”aaab”时。
　　暴力做法是每次的最坏情况就是判断lenT次，而一共要判断lenS个lenT次。那么时间复杂度就是$O(NM)$级别的也就是平方级。
　　然而，KMP是一直往前走，虽然它会回溯，但是最多也只是回溯N次，而且这是基本不可能的。再加上前面M次与自己比较作出next数组（下面在解释next数组的形成，相信我，先别质疑为啥时M次）时间复杂度就是$O(N+M)$级别的，这跟暴力比起来就跟坐火箭一样，但是给我理解感觉上就是暴力的剪枝，就是把不必要的计算给省略了。
　　
　　嗯。我觉得还是用图例来解释对比比较直接生动。
　　
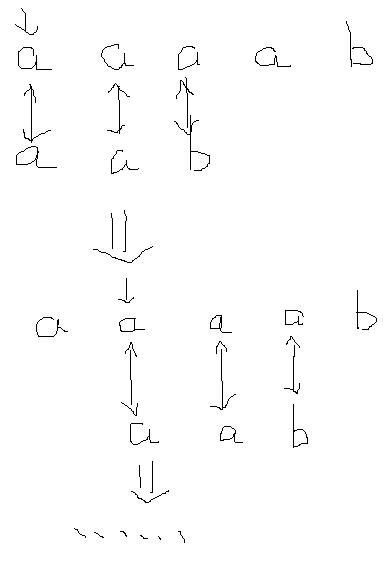
　　暴力：

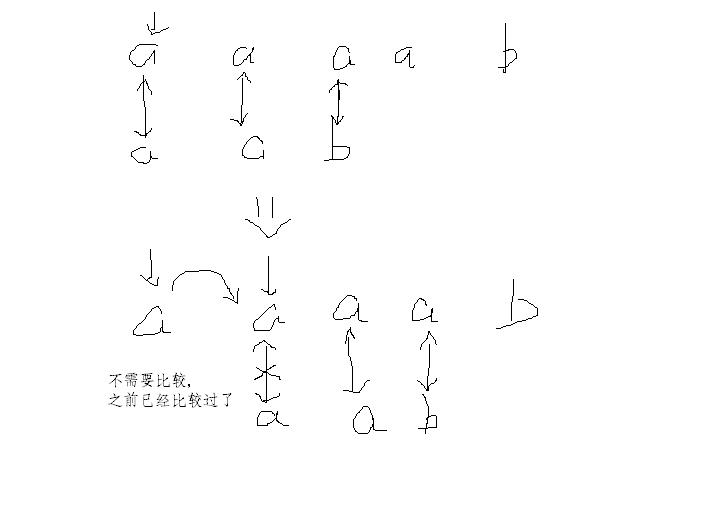
　　KMP：

　　对，next数组就是这么用。就是告诉你哪里已经比较过，已经比较过的地方哪里有可能成功匹配。
　　1
　　好吧好吧，我还是贴程序吧。
　　

next[0]=next[1]=0; k=0;
for (i=2;i<=m;i++)
{ while (k>0&&T[i]!=T[k+1]) k=next[k];
 if (T[i]==T[k+1]) k++;
 next[i]=k;
}

　　这就是求next数组的过程。一共比较lenT次，虽然有回溯，也只是lenT次罢了。所以就是这样。

　　接下来就是这些天的题目与题解。
　　

The French author Georges Perec (1936–1982) once wrote a book, La disparition, without the letter ‘e’. He was a member of the Oulipo group. A quote from the book:
Tout avait Pair normal, mais tout s’affirmait faux. Tout avait Fair normal, d’abord, puis surgissait l’inhumain, l’affolant. Il aurait voulu savoir où s’articulait l’association qui l’unissait au roman : stir son tapis, assaillant à tout instant son imagination, l’intuition d’un tabou, la vision d’un mal obscur, d’un quoi vacant, d’un non-dit : la vision, l’avision d’un oubli commandant tout, où s’abolissait la raison : tout avait l’air normal mais…
Perec would probably have scored high (or rather, low) in the following contest. People are asked to write a perhaps even meaningful text on some subject with as few occurrences of a given “word” as possible. Our task is to provide the jury with a program that counts these occurrences, in order to obtain a ranking of the competitors. These competitors often write very long texts with nonsense meaning; a sequence of 500,000 consecutive ‘T’s is not unusual. And they never use spaces.
So we want to quickly find out how often a word, i.e., a given string, occurs in a text. More formally: given the alphabet {‘A’, ‘B’, ‘C’, …, ‘Z’} and two finite strings over that alphabet, a word W and a text T, count the number of occurrences of W in T. All the consecutive characters of W must exactly match consecutive characters of T. Occurrences may overlap.
Input
The first line of the input file contains a single number: the number of test cases to follow. Each test case has the following format:
One line with the word W, a string over {‘A’, ‘B’, ‘C’, …, ‘Z’}, with 1 ≤ |W| ≤ 10,000 (here |W| denotes the length of the string W).
One line with the text T, a string over {‘A’, ‘B’, ‘C’, …, ‘Z’}, with |W| ≤ |T| ≤ 1,000,000.
Output
For every test case in the input file, the output should contain a single number, on a single line: the number of occurrences of the word W in the text T.
Sample Input
3
BAPC
BAPC
AZA
AZAZAZA
VERDI
AVERDXIVYERDIAN
Sample Output
1
3
0

就是一道模板题。
题解：

/*
1.在字符数组前面插个空: scanf("%s".chr+1); 
    注：这个空不能为0，最好附一个值，因为strlen是根据0的位置确定字符数组长度 
2.在不能空一个位置的时候，可以选择把另一个数组的下标全部+1，数值不变。 
*/

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std ;
int next[10005];
char W[10005],T[1000005];
int main()
{
    int n;
    cin>>n;
    for (int N=0;N<n;N++)
    {
        scanf("%s",W);
        scanf("%s",T);
        int lnW=strlen(W);
        int lnT=strlen(T);
        int ans=0,k;
        memset(next,0,sizeof 0);
        next[0]=next[1]=-1;
        k=-1;
        for (int i=1;i<lnW;i++)
        {
            while(k>-1&&W[i]!=W[k+1])
                k=next[k+1];
            if (W[i]==W[k+1]) k++;
            next[i+1]=k;
        }
        k=-1;
        for (int i=0;i<lnT;i++)
        {
            while(k>-1&&T[i]!=W[k+1]) 
                k=next[k+1];
            if (T[i]==W[k+1]) k++;
            if (k==lnW-1) 
            {
                k=next[k+1];
                ans++;
            }
        }
        cout<<ans<<endl;
    }
    return 0;
}

第二题：

Description
Every morning when they are milked, the Farmer John’s cows form a rectangular grid that is R (1 <= R <= 10,000) rows by C (1 <= C <= 75) columns. As we all know, Farmer John is quite the expert on cow behavior, and is currently writing a book about feeding behavior in cows. He notices that if each cow is labeled with an uppercase letter indicating its breed, the two-dimensional pattern formed by his cows during milking sometimes seems to be made from smaller repeating rectangular patterns.
Help FJ find the rectangular unit of smallest area that can be repetitively tiled to make up the entire milking grid. Note that the dimensions of the small rectangular unit do not necessarily need to divide evenly the dimensions of the entire milking grid, as indicated in the sample input below.
Input
* Line 1: Two space-separated integers: R and C
* Lines 2..R+1: The grid that the cows form, with an uppercase letter denoting each cow’s breed. Each of the R input lines has C characters with no space or other intervening character.
Output
* Line 1: The area of the smallest unit from which the grid is formed
Sample Input
2 5
ABABA
ABABA
Sample Output
2
题解：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std ;
int r[10005],c[80];
char cpy1[10005][80],cpy2[80][10005];
char mat[10005][80];
int main()
{
    int n,m,k;
    scanf("%d%d",&n,&m);
    for (int i=0;i<n;i++)
            scanf("%s",mat[i]);
    for (int i=0;i<n;i++)
        for (int j=0;j<m;j++)
            cpy1[i][j]=mat[i][j];
    r[0]=r[1]=0;
    for (int i=1;i<n;i++)
    {
        k=r[i];
        while(k&&strcmp(cpy1[i],cpy1[k])) k=r[k];
        if (!strcmp(cpy1[i],cpy1[k])) r[i+1]=k+1;
            else r[i+1]=0;
    }
    for (int i=0;i<n;i++)
        for (int j=0;j<m;j++)
            cpy2[j][i]=mat[i][j];
    c[0]=c[1]=0;
    for (int i=1;i<m;i++)
    {
        k=c[i];
        while(k&&strcmp(cpy2[i],cpy2[k])) k=c[k];
        if (!strcmp(cpy2[i],cpy2[k])) c[i+1]=k+1;
            else c[i+1]=0;
    }
    printf("%d\n",(n-r[n])*(m-c[m]));
    return 0;
}

这是一道二维的KMP，只需要把每行每列分别看成时一个字符就好了。再把行和列都乘起来就得出答案了

【赶着吃饭】

END.