三维空间RRT融合人工势场APF算法，并对RRT优化算法规划得到的路径进行平滑处理。 自己在APF和RRT

文章标题：三维空间中RRT与人工势场APF算法的融合及其路径平滑处理

一、引言

在机器人导航和路径规划领域，RRT（快速探索随机树）算法和人工势场APF（Artificial Potential Field）算法是两种常用的算法。RRT算法通过随机采样的方式在复杂环境中快速找到路径，而人工势场法则利用势能场为机器人规划路径。本文将介绍如何在三维空间中融合这两种算法，并对RRT规划得到的路径进行平滑处理。

二、三维空间RRT算法

RRT算法是一种基于采样的路径规划算法，它通过在状态空间中随机选择节点并连接到最近的已知节点来构建路径。在三维空间中，RRT算法可以快速找到一条从起点到终点的路径。然而，由于环境中可能存在的障碍物，RRT规划的路径可能存在抖动和不连续的问题。

三、人工势场APF算法

人工势场法是一种基于局部路径规划的算法。在该方法中，机器人被视为一个受到周围环境势能影响的粒子。通过计算势能梯度，机器人可以确定其运动方向。在三维空间中，人工势场法可以提供更加平滑的路径。然而，该算法在处理复杂环境时可能陷入局部最小值或者死锁。

四、RRT与APF算法的融合

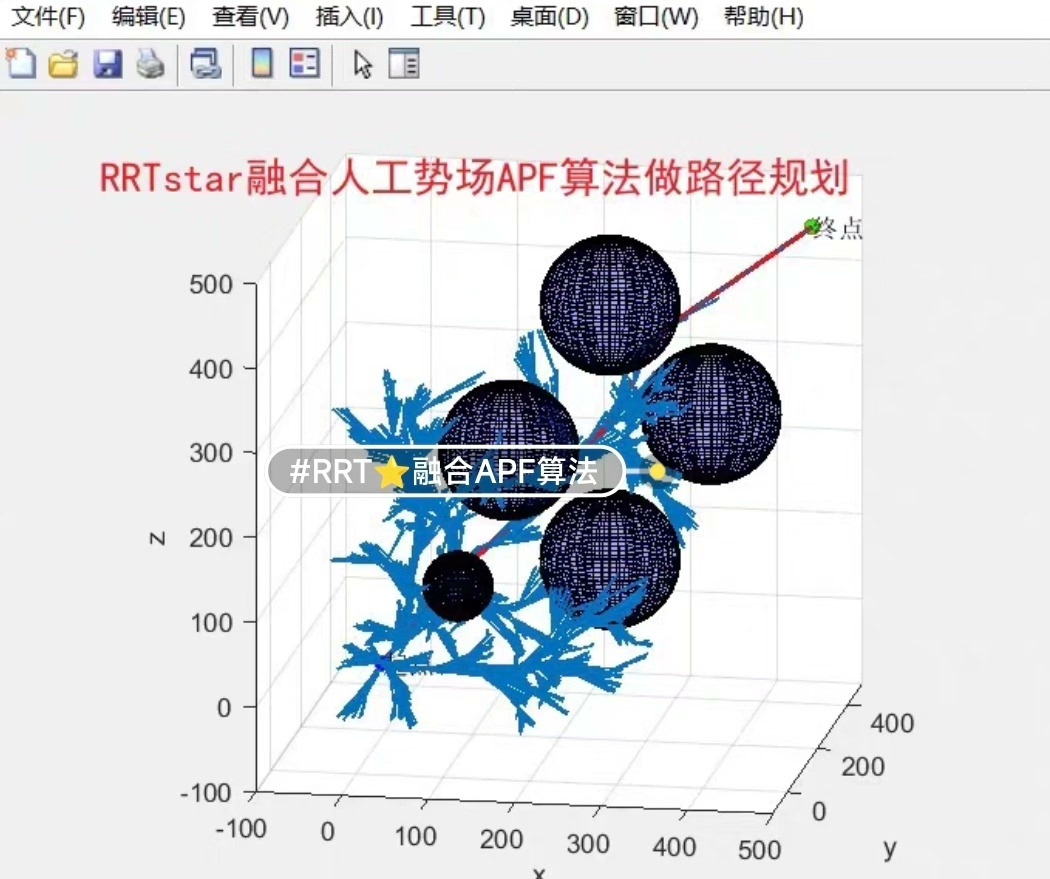
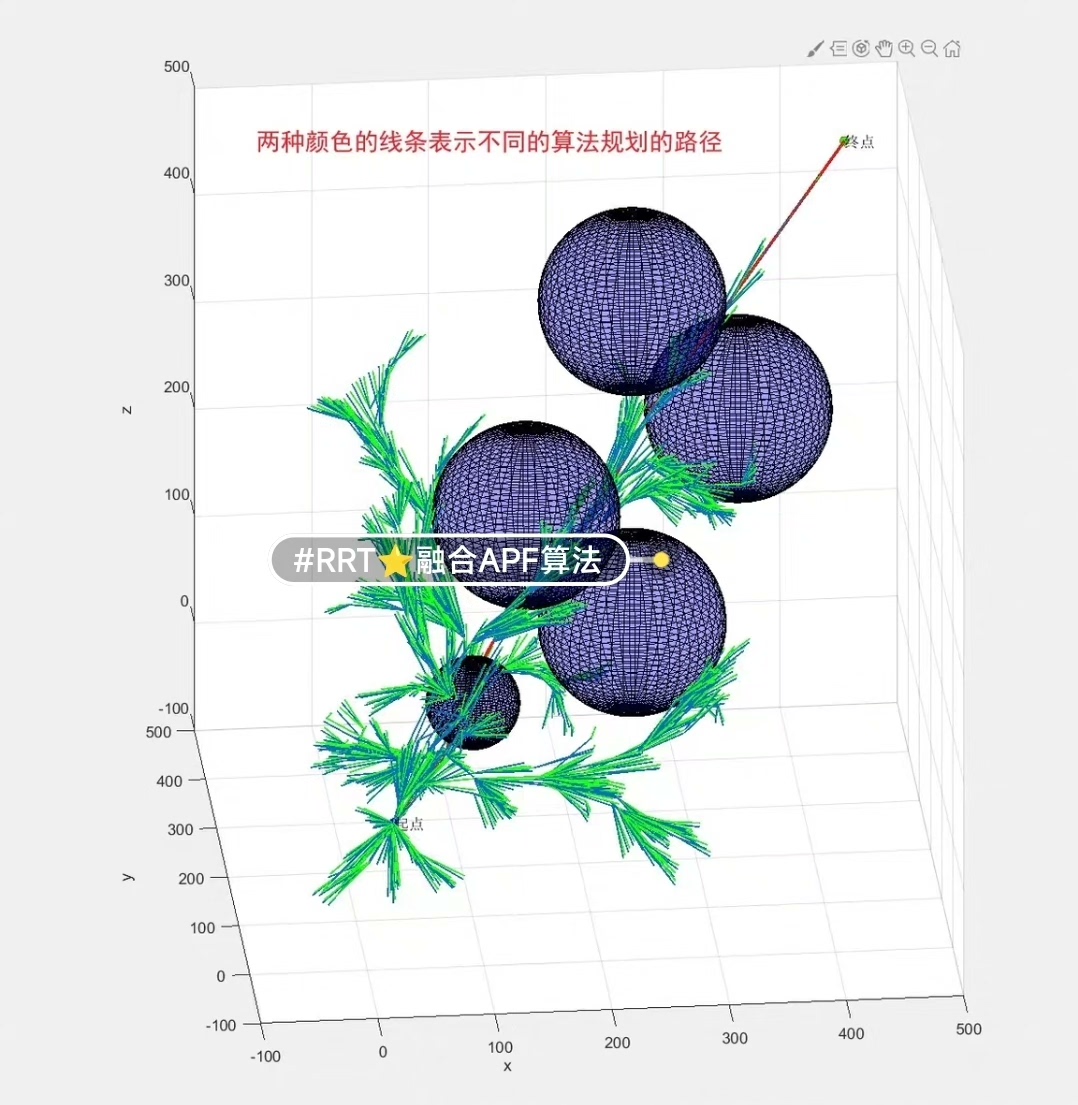
为了充分发挥RRT和APF算法的优点，本文提出了一种在三维空间中融合这两种算法的方法。首先，利用RRT算法快速找到一条初步的路径。然后，在APF算法的势能场中对该路径进行优化，使路径更加平滑且避开障碍物。通过这种方式，我们可以得到一条既快速又平滑的路径。

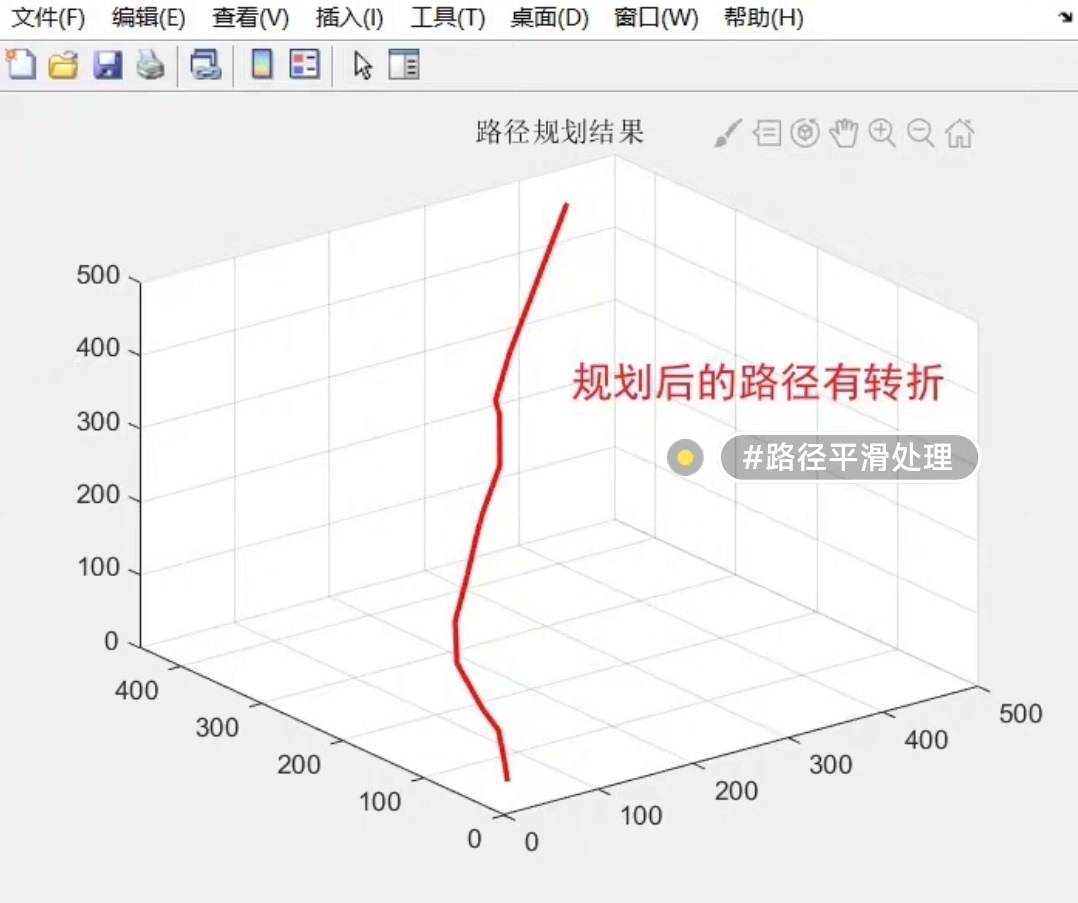
五、RRT规划路径的平滑处理

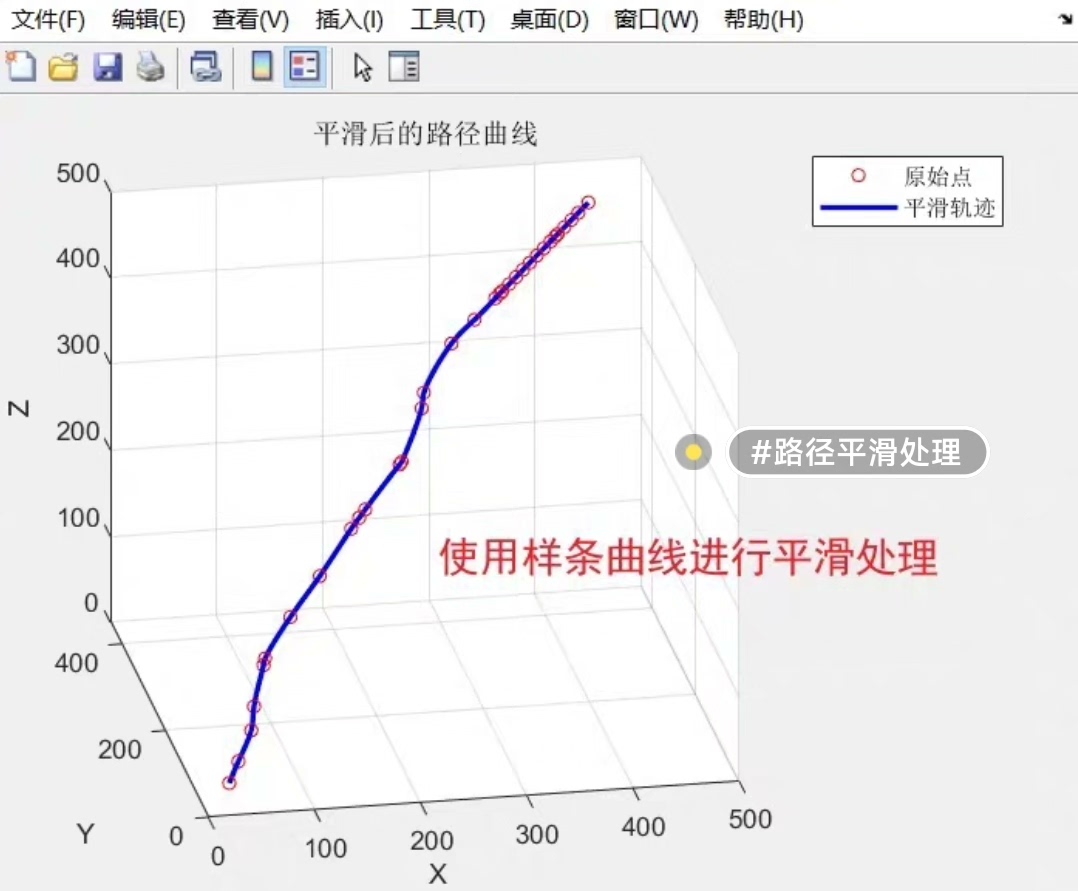
虽然RRT算法可以在复杂环境中快速找到路径，但规划得到的路径可能存在抖动和不连续的问题。为了解决这个问题，我们采用了一种平滑处理的方法。具体来说，我们使用一种基于贝塞尔曲线的平滑算法对RRT规划的路径进行平滑处理。通过调整贝塞尔曲线的控制点，我们可以得到一条更加平滑且连续的路径。

六、代码模块化与改进

为了方便后续的改进和维护，我们将代码进行了模块化设计。每个模块都负责完成特定的功能，如RRT采样、RRT路径构建、APF势能场计算、路径平滑等。通过模块化设计，我们可以更加方便地在此基础上进行改进和扩展。例如，我们可以尝试使用其他平滑算法对路径进行平滑处理，或者引入其他优化策略来进一步提高路径的质量。

七、注释清晰

在编写代码时，我们注重注释的清晰性。每个函数和模块都配备了详细的注释，以便其他开发者能够轻松理解代码的功能和实现方式。此外，我们还提供了详细的文档和说明，以便用户能够更好地使用我们的算法库。

八、结论

本文介绍了一种在三维空间中融合RRT和APF算法的方法，并对RRT规划得到的路径进行了平滑处理。通过模块化设计和清晰的注释，我们提供了一个方便使用的算法库。该算法库可以在机器人导航和路径规划领域中发挥重要作用，为机器人提供更加快速、平滑且安全的路径。未来，我们将继续对该算法进行改进和优化，以提高其性能和适用性。
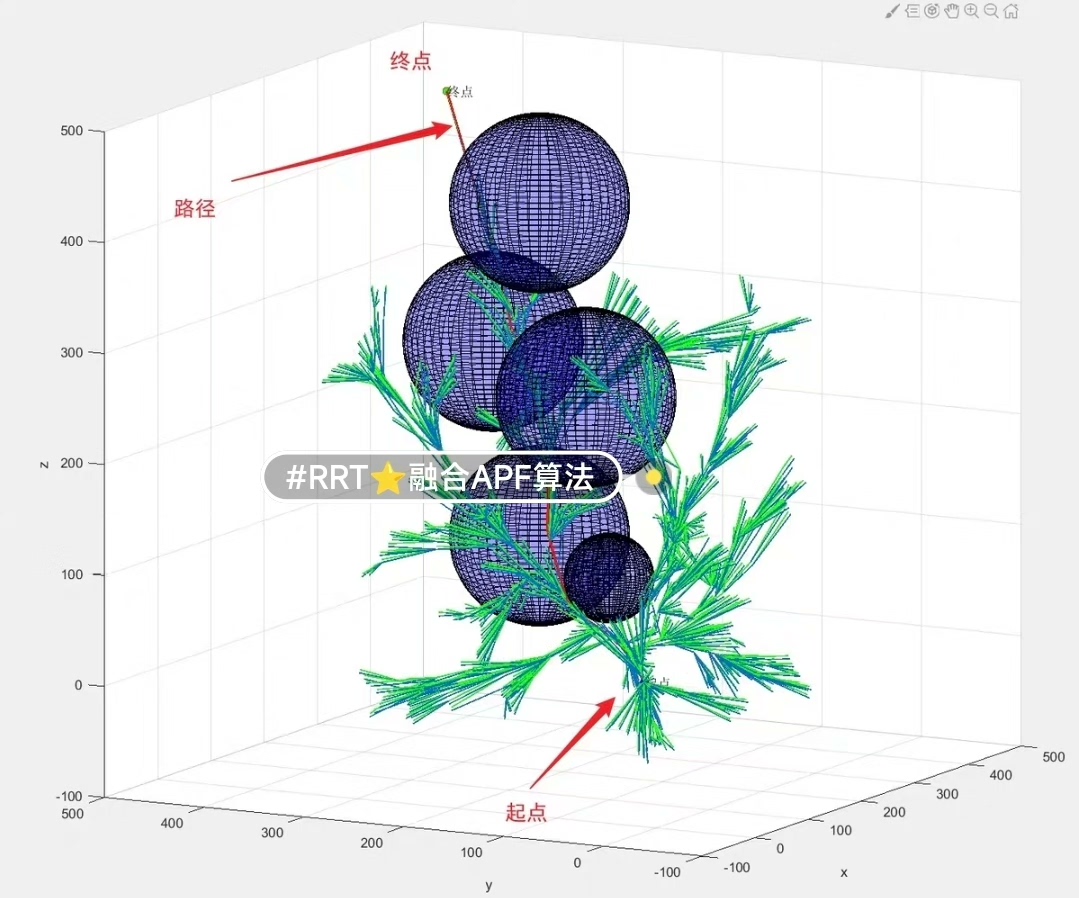
三维空间RRT融合人工势场APF算法，并对RRT优化算法规划得到的路径进行平滑处理。
自己在APF和RRT算法基础上改的，代码模块化好，能在此基础上进行改进。
注释清晰即可。