Lotka-Volterra竞争模型

Odd_guy

已于 2024-01-13 10:29:48 修改

阅读量4.8k

点赞数 8

分类专栏：理论生态学文章标签：经验分享

于 2022-12-16 14:49:14 首次发布

本文链接：https://blog.csdn.net/SUN5_The_answer/article/details/127943893

版权

理论生态学专栏收录该内容

7 篇文章

订阅专栏

一、生态学Tips

1、生态学系统是复杂适应性系统；
2、生态学根植于博物学；
3、不可忽略进化论；
4、生态学事关大自然；
5、了解一点哲学；
6、生态学是有用的科学；
7、生态学不是万能的；
8、类社会科学的学科范式；
9、参考物理学而非工程学来理解生态学的生态位；
10、数学很重要。

二、物种的竞争

1、Lotka-Volterra竞争模型

假设有一草地，其共同的“捕食者”是兔子和羊，且二者在假定的草地生态系统中存在竞争关系。
有：
$\begin{cases} 对兔子（N_{1}）:\frac{\text{d}N_{1}}{\text{d}t}=r_{1}\cdot N_{1}(1-\frac{N_{1}}{K_{1}}）\\ 对羊有（N_{2}）:\frac{\text{d}N_{2}}{\text{d}t}=r_{2}\cdot N_{2}(1-\frac{N_{2}}{K_{2}}） \end{cases}$
为了将两个方程联系起来，引入变量 $M$ ，表示食草动物动物的食草量，有：
$M_{羊}=\alpha\cdot M_{兔}$
因此可得到两个相对竞争系数，分别是羊对兔的 $\alpha_{1\leftarrow2}$ 和兔对羊的 $\alpha_{2\leftarrow1}$ ，以及两个种内的密度制约系数 $\alpha_{1\leftarrow1}$ 、 $\alpha_{2\leftarrow2}$ ，带入两个式子可得：
$\begin{cases} \frac{\text{d}N_{1}}{\text{d}t}=r_{1}\cdot N_{1}（1-\alpha_{1\leftarrow1}\frac{N_{1}}{K_{1}}-\alpha_{1\leftarrow2}\frac{N_{2}}{K_{1}}）\\ \frac{\text{d}N_{2}}{\text{d}t}=r_{2}\cdot N_{2}（1-\alpha_{2\leftarrow2}\frac{N_{2}}{K_{2}}-\alpha_{2\leftarrow1}\frac{N_{1}}{K_{2}}）\\ \end{cases}$
此即Lotka-Volterra竞争模型。

2、 $N_{1}、N_{2}$ 的关系

为了探究 $N_{1}、N_{2}$ 的关系，令 $\frac{\text{d}N_{1}}{\text{d}t}=0$ ，解得：
$\begin{cases} N_{1}=0\\ 1-\alpha_{1\leftarrow1}\frac{N_{1}}{K_{1}}-\alpha_{1\leftarrow2}\frac{N_{2}}{K_{1}}=0 \end{cases}$
且：有 $K_{1}>1$ ，所以，等式两边同时乘 $K_{1}$ 得：
$K_{1}-\alpha_{1\leftarrow1}\cdot N_{1}-\alpha_{1\leftarrow2}\cdot N_{2}=0$
整理得：
$\frac{K_{1}}{\alpha_{1\leftarrow2}}-\frac{\alpha_{1\leftarrow1}\cdot N_{1}}{\alpha_{1\leftarrow2}}=N_{2}$
因为： $\frac{K_{1}}{\alpha_{1\leftarrow2}}、\frac{\alpha_{1\leftarrow1}}{\alpha_{1\leftarrow2}}$ 为常数，所以 $N_{1}、N_{2}$ 的关系是二维坐标系上的一条直线。

3、竞争结果

当忽略两个种群内部同种个体间的相互关系 $\alpha_{1\rightarrow1}$ 和 $\alpha_{2\rightarrow2}$ ，同时将 $\alpha_{1\rightarrow2}$ 和 $\alpha_{2\rightarrow1}$ 简写为 $\alpha_{12}$ 和 $\alpha_{21}$ 时，方程可表示为：
$\begin{cases} N_{1}'=r_{1}\cdot N_{1}（1-\frac{N_{1}}{K_{1}}-\alpha_{12}\frac{N_{2}}{K_{1}}）\\ N_{2}'=r_{2}\cdot N_{2}（1-\frac{N_{2}}{K_{2}}-\alpha_{21}\frac{N_{1}}{K_{2}}）\\ \end{cases}$
当生境内完全被 $N_{1}$ 或被 $N_{2}$ 占据时，针对两个式子，可分别在坐标系上获取两个点：
$\begin{cases} 兔(N_{1})：(K_{1},0),(0,\frac{K_{1}}{\alpha_{12}})\\ 羊(N_{2})：(0,K_{2}),(\frac{K_{2}}{\alpha_{21}},0) \end{cases}$
分别针对两个种群绘图，根据Logistic方程，分别获得两组矢量关系图（箭头方向表示种群大小变化方向）。
在这里插入图片描述

将两组矢量关系图结合，即可推测四种不同的竞争结果。

（1） $N_{1}$ 兔获胜

当 $K_{1}>\frac{K_{2}}{\alpha_{21}}$ ， $\frac{K_{1}}{\alpha_{12}}>K_{2}$ 时：
在这里插入图片描述

（2） $N_{2}$ 羊获胜

当 $K_{2}>\frac{K_{1}}{\alpha_{12}}$ ， $\frac{K_{2}}{\alpha_{21}}>K_{1}$ 时：
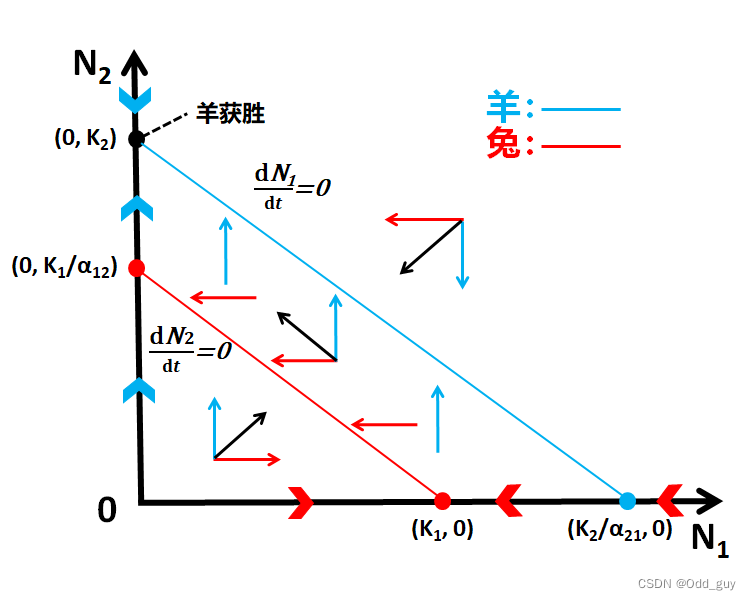
在这里插入图片描述

（3）稳定共存（一个平衡点）

当 $\frac{K_{2}}{\alpha_{21}}>K_{1}$ ， $\frac{K_{1}}{\alpha_{12}}>K_{2}$ 时：
在这里插入图片描述

（4）无法预测（无平衡点）

当 $K_{1}>\frac{K_{2}}{\alpha_{21}}$ ， $K_{2}>\frac{K_{1}}{\alpha_{12}}$ 时：
在这里插入图片描述

4、多种群的竞争关系

现在，我们获得了两个种群的竞争关系，并预测了四种可能的情形，那多个种群的竞争关系是如何的呢？
在前面的推到中，我们忽略了种群内部的同种个体的相互关系（ $\alpha_{11}、\alpha_{22}$ ），现将其重新加入到（物种数 $n = 2$ ）关系式中：
$\begin{cases} \frac{\text{d}N_{1}}{\text{d}t}=r_{1}N_{1}(1-\alpha_{11}\frac{N_{1}}{K_{1}} -\alpha_{12}\frac{N_{2}}{K_{1}})\\ \frac{\text{d}N_{2}}{\text{d}t}=r_{2}N_{2}(1-\alpha_{22}\frac{N_{2}}{K_{2}} -\alpha_{21}\frac{N_{21}}{K_{2}}) \end{cases}$
通过观察两物种的关系式可发现，括号内的各物种关系可以以和的形式表示，即：
$\sum_{j=1}^{n}{\alpha_{ij}\frac{N_{j}}{K_{i}}}$
由此可知，在一个含 $n$ 个物种的生境内（物种丰度为 $n$ ），第 $i$ 个物种种群大小变化的函数关系为：
$\frac{\text{d}N_{i}}{\text{d}t}=r_{i}N_{i}(1-\sum_{j=1}^{n}{\alpha_{ij}\frac{N_{j}}{K_{i}}})$
观察函数关系式可发现两个重要的状态变量（见Module 1）： $\alpha_{ij}、n$ ，分别表示物种丰富度（ $n$ ）和种间或种内交互系数（ $\alpha_{ij}$ ）。
Module 1：

以理想气体方程为例：
PV=nRT
通过只描述气体状态的状态变量，例如p为压强（Pa），V为气体体积(m³)，来描述空间内的气体。

我们是否可以通过这两个状态变量类模拟群落的动态竞争关系呢？
具体内容可参考胡脊梁的文章，DOI: 10.1126/science.abm7841