FDTD中光源的实现

SimWorks光仿软件

于 2025-04-29 16:39:18 发布

阅读量1k

点赞数 35

文章标签： FDTD 光学光电仿真光源

本文链接：https://blog.csdn.net/SimWorks/article/details/147613424

版权

前言

光波作为电磁波之一，是由光源辐射出的，任何能发光的物体都可称为光源。在现实生活中，常见的光源包括热光源、气体放电光源和激光器等，与我们日常生活密不可分的太阳也是属于一种发出连续光谱的热光源。这些光源各自具有独特的发光特性和应用场景。而在电磁仿真领域，为了模拟光源的行为，存在各种光源模型，如高斯光源、点光源等，用于描述不同类型光源的辐射特性。下图为太阳光辐射到外大气层的光谱图（AM0）。

在之前的文章当中，我们已经简要介绍了时域有限差分法（FDTD），它作为一种电磁仿真领域经典的数值求解方法，被广泛应用于光学器件设计、天线分析、电磁兼容性等研究领域。本文将继续介绍如何在该方法当中引入各种光源模型。正确地选择和优化光源模型及参数，对于保证仿真结果的准确性和可靠性至关重要。

FDTD中的激励源

在FDTD方法当中，对于已经构建好的Yee cell网格，如何采用适当方法将入射波加入到FDTD迭代中是一个重要课题。对于激励源，可以从时域/频域以及空间分布等方面进行分析。

激励源的时间信号

从时域信号上看，各种激励源大致有两类：一种是随时间周期变化的时谐场源，另一种则是脉冲信号的波源。时谐场源一般使用正余弦函数作为其基本波形。常见的正弦时谐波为

$E_{i}(t)=\begin{cases} 0 & \text t< 0\\ E_{0} sin(w_0t) & \text t>0 \end{cases}$

这是一个半无限的正弦波列，理论上当采样点无限时，其频谱即为单频点。

而脉冲波源的频谱具有一定的带宽，由于实际光源大部分都为宽频带，因此在FDTD数值计算当中大多采用脉冲波源。常见的脉冲信号有高斯脉冲，矩形脉冲（方波），单周期正弦脉冲等。以下简单介绍调制高斯脉冲的时域频域特征。余弦调制高斯脉冲，即高斯脉冲信号乘以一个余弦调制函数，来控制脉冲的起始时间和幅度等特性，用以满足不同领域对脉冲信号的需求。此时其时域形式为:

$E_i(t)=-cos(w_0t)exp(-\cfrac{4\pi(t-t_0)^2}{\tau^2})$

其中 $w_0=2\pi f_0$ ， $f_0$ 为中心频率。其时域波形与频谱如下所示:

激励源的加入方式

在FDTD数值计算当中，激励源的加入方式大致有以下两种。一种是指在仿真空间中的一个点或面上设置固定的辐射强度，其辐射特性不随空间位置变化而改变。以一维FDTD为例，在原点处将Ex分量赋值为高斯脉冲，其在FDTD的传播情况如下。

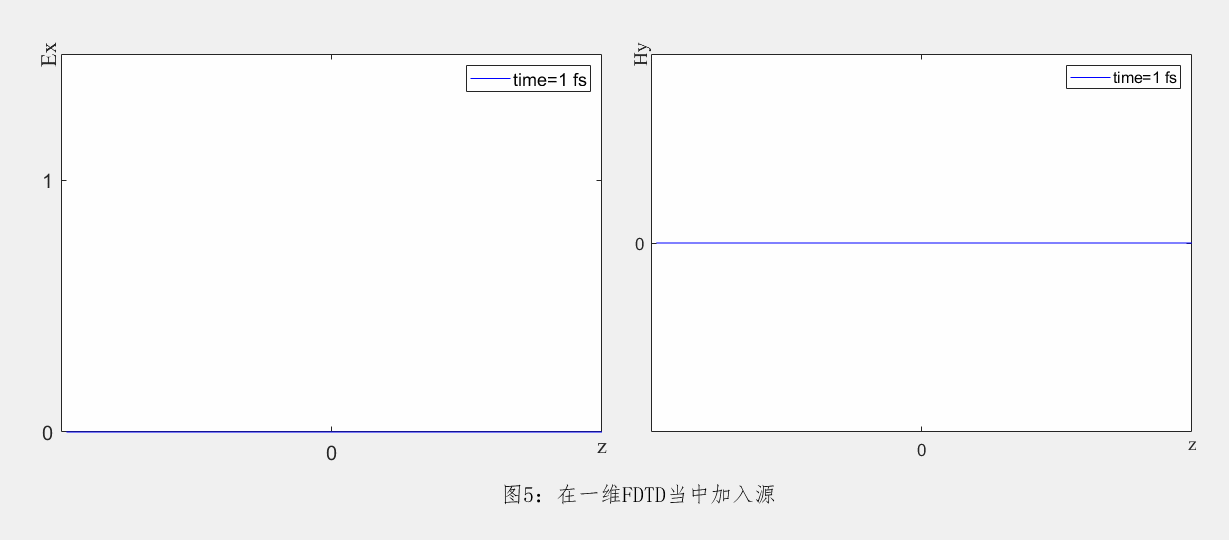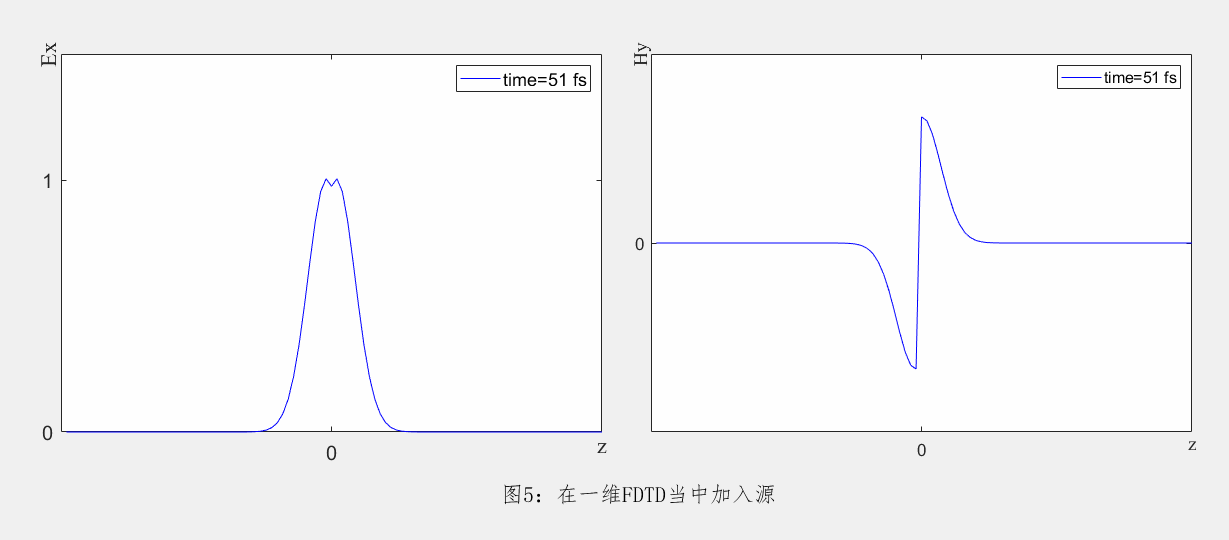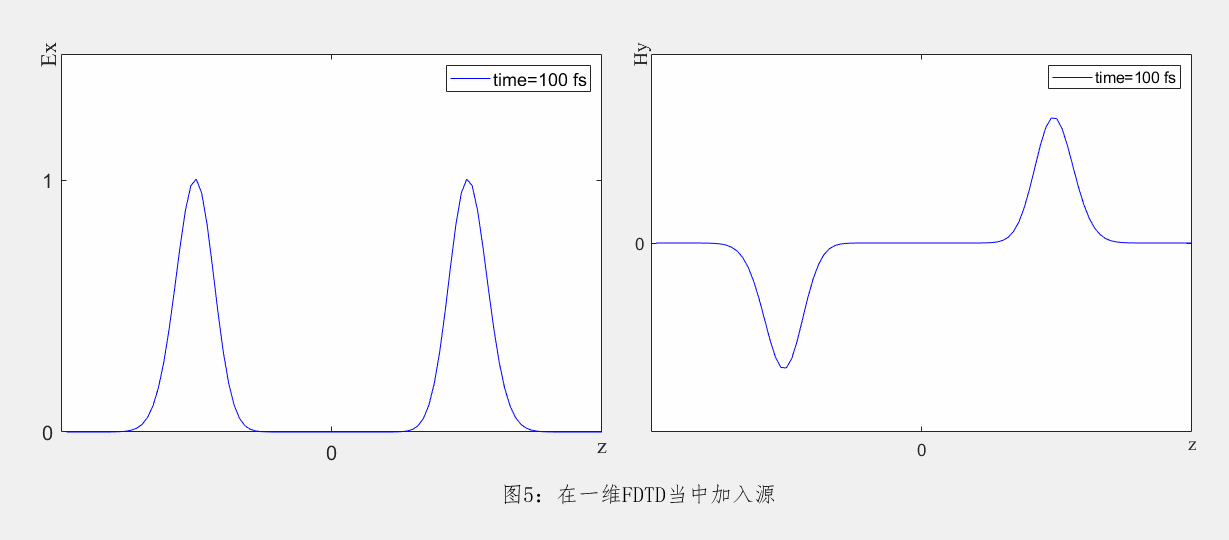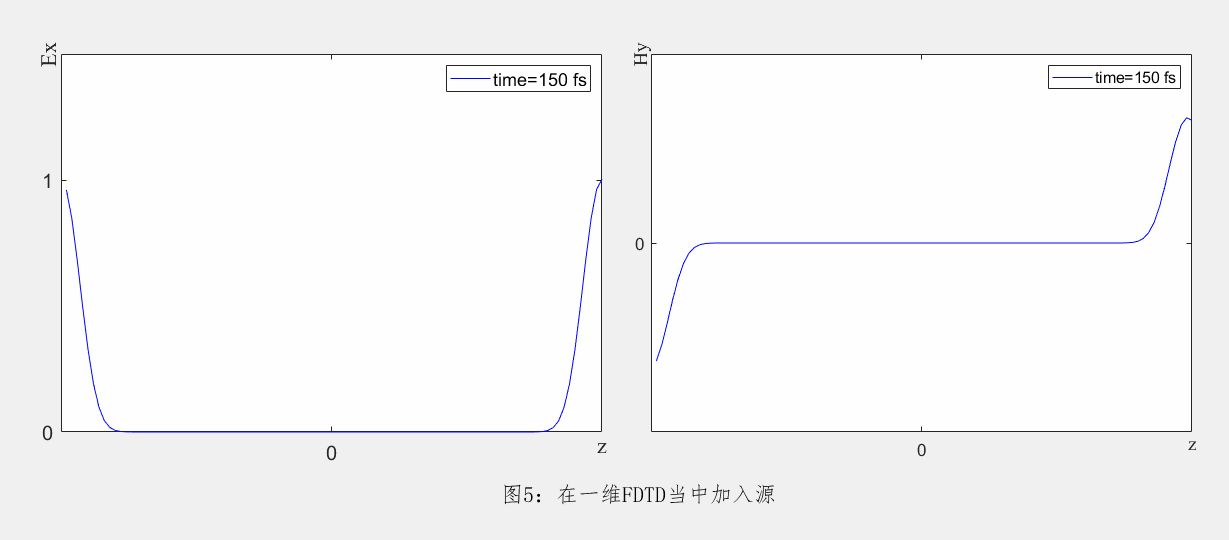
另一种加源方式根据麦克斯韦方程，将源的看作为电流或者磁流代入迭代方程。这种设置可以模拟具有特定辐射模式的光源，其辐射强度可以随空间位置变化而变化。以在二维TE FDTD当中添加磁流为例，当元胞内磁流密度 $J_m=\cfrac{I(t)}{\Delta x \Delta y}$ ，将该电流源加入FDTD迭代方程当中即可得到

$Hz|_{i+1/2,j+1/2}^{n+1/2}=DA*Hz|_{i+1/2,j+1/2}^{n-1/2}+DB*[\nabla \times E]_{i+1/2,j+1/2}^{n}-DB*\cfrac{I^{n}}{\Delta x \Delta y}$

第一种加源方式未考虑过回波的存在，在回波传播到光源位置会产生不必要的反射。而第二种加源方式则可以避免这种反射，同时可以根据光源的空间分布按上式赋值给网格当中对应的分量，从而更准确地模拟实际光源的行为。

在FDTD数值计算中，我们可以根据需要选择合适的激励源类型和空间分布，以模拟不同光源的辐射特性。通过不同的加源方式，更好地描述光源在网格空间中的行为，并对光场的传播和相互作用过程进行准确的模拟和分析。合理选择和设置光源的空间分布对于准确模拟光学器件的行为具有重要意义。

激励源的空间分布

在FDTD中，光源的空间分布指的是光源的辐射强度如何随空间位置变化。由于在FDTD中，电磁场在Yee cell空间以半个网格交错分布，这种离散划分，使得光源的空间分布也需要遵从这种规则。而不同类型的光源，如点源，线源，面源等在空间上的加源方式也各不相同。我们需要在仿真空间的不同位置设置适当的辐射强度来引入不同的光源，这对于模拟不同类型的光源行为至关重要。

平面波光源

在光源的传播过程当中，我们假定在一个无限大的各向同性均匀介质当中，没有自由电荷以及传导电流的存在（ $\rho=0,j=0$ ），此时可以简化麦克斯韦方程组的微分形式，得到以下结果

$\begin{cases} \nabla \cdot \mathbf{E} = 0 \\ \nabla \cdot \mathbf{H} = 0 \\ \nabla \times \mathbf{E} = - {\cfrac{\partial \mathbf{B}}{\partial t}}\\ \nabla \times \mathbf{H} = {\varepsilon}{\mu}{\cfrac{\partial \mathbf{E}}{\partial t}} \end{cases}$

取第三式的旋度并代入第四式即可得到

$\nabla ^2 \mathbf{E} - {\varepsilon}{\mu}{\cfrac{\partial^2 \mathbf{E}}{\partial t^2}} = 0$

同理可得磁场 $\mathbf{H}$ 的方程，联立即为波动方程（ $v=\cfrac{1}{\sqrt{\varepsilon \mu}}$ ）

$\begin{cases} \nabla ^2 \mathbf{E} -\cfrac{1}{v^2}{\cfrac{\partial^2 \mathbf{E}}{\partial t^2}} = 0 \\ \nabla ^2 \mathbf{H} -\cfrac{1}{v^2}{\cfrac{\partial^2 \mathbf{H}}{\partial t^2}} = 0 \end{cases}$

波动方程一般情况下没有通解，我们需要在具体的边界条件和初始条件下来描述波的传播和振动行为。

而平面波解作为波动方程一种最基本的特解，于是我们可以求解出沿z方向上传播的平面波，其复数形式的解如下

$\mathbf{E}=\mathbf{A}exp(i\mathbf{k} \cdot \mathbf{r})exp(-iwt)$

其中 $\mathbf{k}$ 为波矢量，其大小波数为 $k=2\pi/\lambda$ ， $w$ 为角频率，大小为 $w=2\pi f$ 。可以看到其位相因子分为两部分，前者为空间因子 $exp(i(\mathbf{k} \cdot \mathbf{r}))$ ，后者为时间位相因子 $exp(-iwt)$ 。此时平面简谐波传播时的时间位相因子都相同，故仅需要一个复振幅 $\mathbf{\tilde{E}}=\mathbf{A}exp(i(\mathbf{k} \cdot \mathbf{r}))$ 来表示一个平面简谐波。

当选取一个二维考察平面(xOy 面)，假定波矢量 $\mathbf{k}$ 与xz平面平行，并按如上左图所示入射，上式在考察平面上的振幅分布为

$\mathbf{\tilde{E}}=\mathbf{A}exp(ikxcos\alpha)=\mathbf{A}exp(ikxsin\gamma)$

如图8中右图所示，可以看到等相线是平面波的等相面与 $z=0$ 平面的交线。故我们可以知道，当平面波垂直入射时，在Yee-cell网格当中光源所在位置的直线上设置完全相同，而倾斜入射时也仅需进行插值即可。

总场散射场光源

当需要对某一散射体进行研究时，总场散射场（Total-field Scattered-field,TFSF）是一种有效的光源设置。它将仿真区域分为两部分，一部分只存在总场（即为入射场与散射场的叠加），另一部分则只存在散射场，两者的连接边界可以消除总场当中的入射场，从而使得散射场当中仅有散射场的存在。

以下以二维TE模式下TFSF光源为例进行介绍，在该连接边界上，即可以利用一维平面波的传播场作为入射场进行修正。经过修正后，当总场当中不存在散射体时，总场中的场分布将与平面波光源一致，而散射场当中则没有电磁场传播。 $\begin{cases} E_{x,total}|_{i+1/2,k}^{n+1}=\{E_{x,total}|_{i+1/2,k}^{n+1}\}-CB \cdot \{H_{z,inc}|_{i+1/2,k-1/2}^{n+1/2}\} \\ H_{z,scat}|_{i+1/2,k-1/2}^{n+1/2}=\{H_{z,scat}|_{i+1/2,k-1/2}^{n+1}\}+DB \cdot \{E_{x,inc}|_{i+1/2,k}^{n}\} \end{cases}$

而在实际二维TFSF光源的引入，需要四个连接边界，需要对于每个连接边界的场分量进行类似的修正。同时在斜入射时则需要对不同的连接边界进行相位匹配，情况会更复杂，这里就不详述了。

下图为TFSF光源正入射一个散射体小球，场在FDTD空间的传播情况。

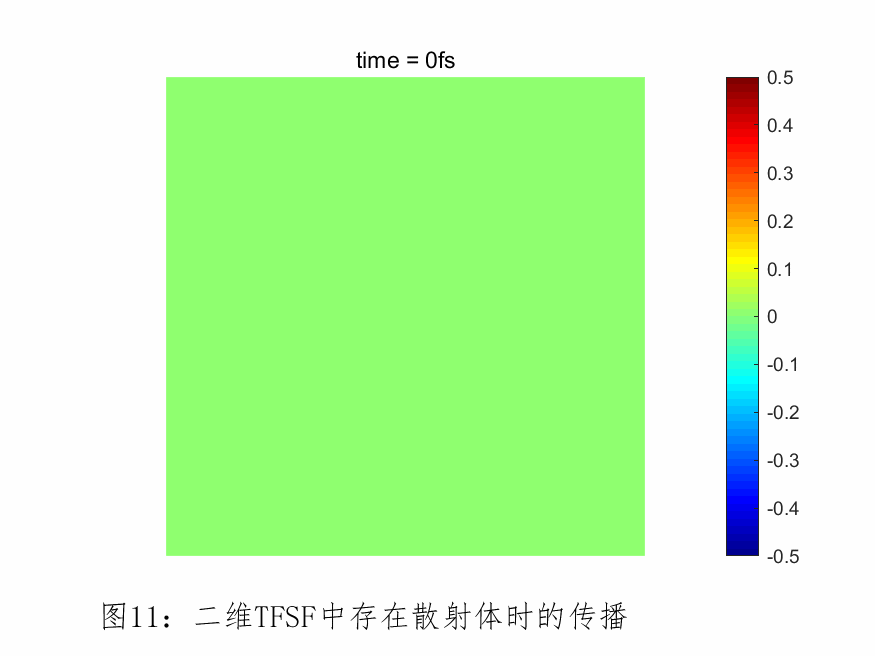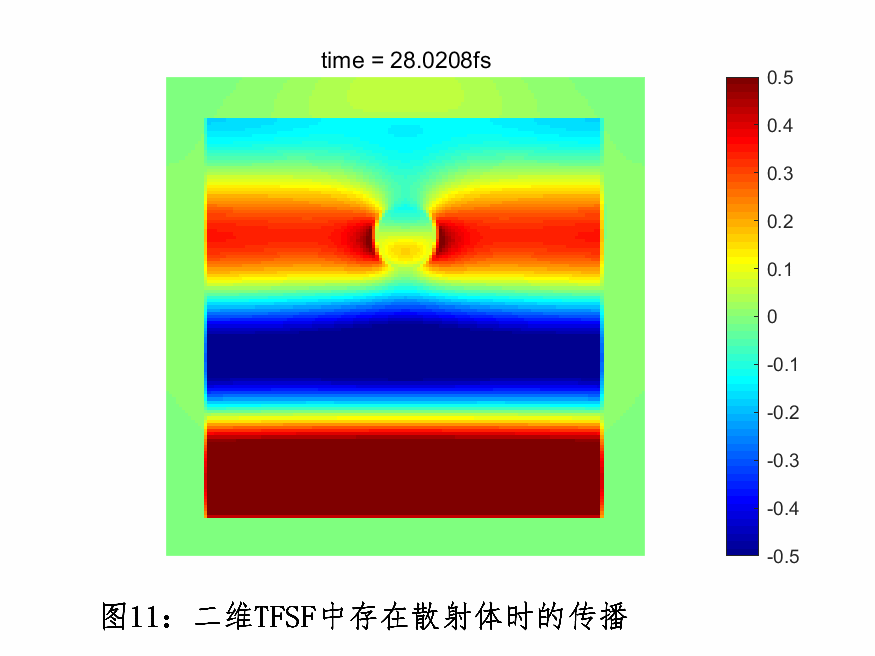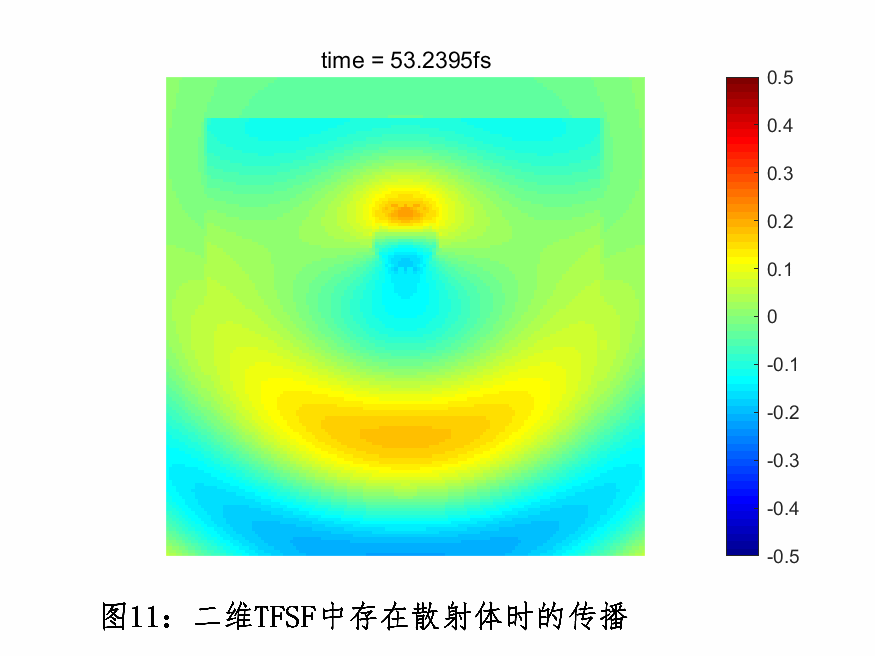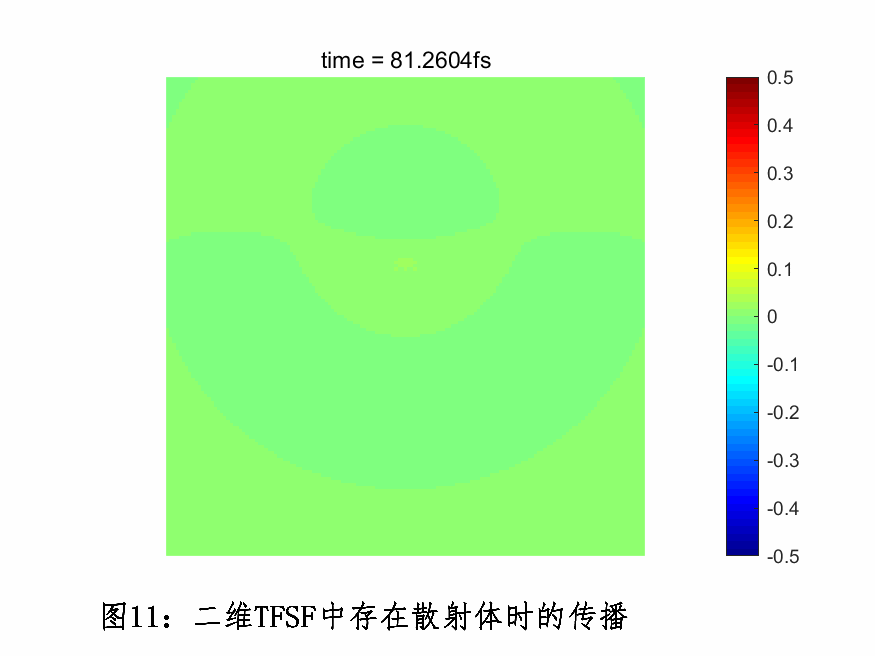
偶极子光源

光源发光的过程可以认为物体在辐射电磁波。一个物体从微观角度上可以认为是由大量分子原子组成，大部分物体发光都为原子发光。经典电磁场理论把原子发光看做是原子内部过程形成电偶极子的辐射。此时原子内部带正电的原子核与带负电的电子相互作用，从而形成一个振荡的电偶极子，它也必定在周围空间当中产生交变的电磁场，即辐射出光波。

我们构建一个简单的电偶极子模型，此时两个符号相反的电荷 $q$ 距离为 $l$ ，故电偶极距为 $p=ql$ ，而电流密度与电偶极矩有如下关系：

$\int\mathbf{J}dV=\cfrac{d\mathbf{p}}{dt}$

将其代入麦克斯韦方程

$\nabla \times \mathbf{H}=\cfrac{\partial \mathbf{D}}{\partial t}+\mathbf{J}$

在单个正方体FDTD元胞当中，假定元胞边长为 $\delta$ ，则上式麦克斯韦方程可写为：

$\varepsilon_0 \cfrac{\partial \mathbf{E}}{\partial t}=\nabla \times \mathbf{H}-\cfrac{1}{\delta^3}\cfrac{d\mathbf{p}}{dt}$

对上式按FDTD方式进行差分离散，可得z分量计算结果如下：

$E_z^{n+1}=E_z^n+\cfrac{\Delta t}{\varepsilon}[\nabla \times \mathbf{H}]_z^{n+1/2}-\cfrac{\Delta t}{\varepsilon_0\delta^3}[\cfrac{dp}{dt}]^{n+1/2}$

在电偶极子所在区域将激励源加入到上式电场节点当中即可实现电偶极子光源的引入。磁偶极子同理加入到对应的磁场节点当中即可。

高斯光源

高斯光束是大部分激光器输出的理想光束，其横截面的辐射照度分布符合高斯函数，因此得名。高斯光束并不是理想的平面波，其在传输轴线附近可近似是一种非均匀球面波。并且其光斑半径按照双曲线规律变化。对高斯光束的研究，是了解与激光有关的众多现象的先决条件。基本高斯光束可以在均匀介质和类透镜系统中求解波动方程得到，其表达式为

$E(x,y,z)=E_0 \cfrac{\omega_0}{\omega(z)}exp[-\cfrac{r^2}{\omega^2(z)}]exp\{ -i[kz-tan^{-1}(\cfrac{z}{z_0})+\cfrac{kr^2}{2R(z)}] \}$

其中 $z_0$ 为准直距离， $R(z)$ 为与传播轴线相较于z点的高斯光束等相位面的曲率半径， $\omega(z)$ 是与传播轴线相交于z点高斯光束的光斑半径， $r=\sqrt{x^2+y^2}$ 。由该解可以得到高斯光束的振幅分布为

$|E|=E_0\cfrac{\omega_0}{\omega(z)}exp[-\cfrac{r^2}{\omega^2(z)}]$

由此可知，高斯光源在z平面上，场振幅以高斯函数从中心向外平滑的减小，同时光斑半径随坐标z按双曲线的规律而扩展：

$\cfrac{\omega^2(z)}{\omega_0^2}-\cfrac{z^2}{z_0^2}=1$

当 $z=0$ 时， $\omega(0)=\omega_0$ 达到最小值，即为光束的束腰半径。

根据上述可以得到在均匀介质传播的基本高斯光束的空间场分布。如下图所示结果

模式光源

模式光源一般使用在光波导当中。在添加模式光源时，我们需要先在光波导结构横截面上进行本征模式求解（FDE解模），以获得所需模式光源的频率、空间分布等信息。然后从解出得TE或TM模式中选择一种，并将其引入到FDTD迭代中。关于FDE解模的详细内容，您可以参考FDE解模。一旦确定所选模式光源的场分布，我们可以按照与高斯光源相同的方式将能量分配到FDTD网格中，从而得到对应的模式光源。下图展示了3D结构的FDE解模结果以及引入模式源后的传输场

参考文献:

[1] Yee K S , "Numerical solution of initial boundary value problems involving maxwell's equations in isotropic media"[J].IEEE Transactions on Antennas & Propagation, 1966, 14(5):302-307.

[2] Allen Taflove, "Computational Electromagnetics: The Finite-Difference Time-Domain Method", Boston:Artech House, (2005).

[3] John B. Schneider, "Understanding the Finite-Difference Time-Domain Method", www.eecs.wsu.edu/~schneidj/ufdtd, (2010).

[4]D.K. Cheng, "Field and Wave Electromagnetics"[M]. Pearson Education Limited, 2014.

[5]"FDE Solver Physics", www.emsimworks.com/zh-CN/solver/FDE.

[6]梁铨廷.物理光学[M].电子工业出版社,2018.

[7]葛德彪,闫玉波.电磁波时域有限差分方法[M].西安电子科技大学出版社,2002.