《Joint Geometrical and Statistical Alignment for Visual Domain Adaptation》学习
2017 CVPR
文章目录
摘要
本文提出了一种用于跨域视觉识别的无监督域自适应算法。我们提出了一个统一的框架,可以在统计和几何上减少域之间的偏移,称为联合几何和统计对齐(JGSA)。
具体而言,我们学习了两种耦合投影,它们将源域和目标域数据投影到低维子空间中,在低维子平面中,几何位移和分布位移同时减少。目标函数可以以闭合形式有效求解。
大量实验证明,在合成数据集和三种不同的真实世界跨域视觉识别任务上,该方法明显优于几种最先进的域自适应方法
一、介绍
可以使用一种现实的策略,即域自适应,来利用先前标记的源域数据来提升新目标域中的任务。
根据目标标记数据的可用性,域自适应一般可分为半监督域自适应和非监督域自适应。
然而,在半监督和非监督域自适应中,都需要足够的未标记目标域数据。在本文中,我们重点讨论了无监督的领域自适应,这被认为是更实际和更具挑战性的。
最常用的领域自适应方法包括基于实例的自适应、特征表示自适应和基于分类器的自适应
在无监督域自适应中,由于目标域中没有标记数据,基于分类器的自适应是不可行的。
或者,我们可以通过最小化域之间的分布差异以及经验源误差来处理这个问题
通常假设可以通过基于实例的自适应方法来补偿分布发散,或者通过基于特征变换的方法
基于实例的方法需要严格的假设,即
- 源域和目标域的条件分布相同,
- 源域中的某些数据可以通过重新加权重新用于目标域中的学习。
而基于特征变换的方法放松了这些假设,仅假设存在两个域分布相似的公共空间。
本文采用基于特征变换的方法。
文献中确定了两类主要的特征变换方法,即数据中心方法和子空间中心方法。
数据中心方法:寻求将两个域的数据投影到域不变空间的统一变换,以减少域之间的分布差异,同时在原始空间中预处理数据属性
子空间中心方法:通过操纵两个域的子空间来减少域偏移,使得每个单独域的子空间都有助于最终映射
利用了特定于域的特征。
例如,Gong等人[10]将两个子空间视为格拉斯曼流形上的两点,并在它们之间的测地线路径上寻找点,作为源子空间和目标子空间之间的桥梁。
Fernando等人[11]使用线性变换矩阵直接对齐源子空间和目标子空间。然而,以子空间为中心的方法仅对两个域的子空间进行操作,而没有精确考虑两个域投影数据之间的分布偏移
我们学习两个耦合投影,将源数据和目标数据映射到各自的子空间
投影后,
- 最大化目标域数据的变化以保留目标域数据属性,
- 保留源数据的鉴别信息以有效传递类别信息,
- 最小化源域和目标域之间的边缘和条件分布差异以在统计上减少域偏移,
- 将两个投影的发散度限制为较小,以在几何上减少域偏移。
因此,与以数据为中心的方法不同,我们不需要强有力的假设,即统一变换可以减少分布偏移,同时保留数据属性。
与以子空间为中心的方法不同,我们不仅减少了子空间几何的偏移,而且减少了两个域的分布偏移。
此外,我们的方法可以很容易地扩展到内核化版本,以处理域之间的移位是非线性的情况。可以以闭合形式有效地求解目标函数。
二、相关工作
2.1以数据为中心的方法
Pan等人提出了转移成分分析(TCA),以使用最大平均差异(MMD)学习RKH中跨域的一些转移成分。
联合分布分析(JDA)通过使用目标域的伪标签,不仅考虑边缘分布偏移,而且考虑条件分布偏移,改进了TCA。
传输联合匹配(TJM)通过联合重新加权实例并找到公共子空间来改进TCA。
分散组件分析(SCA)考虑了源域的类间和类内分散。
然而,这些方法需要一个强有力的假设,即存在一个统一的变换,以将源域和目标域映射到一个具有小分布偏移的共享子空间中。
2.2子空间中心法
如前所述,以子空间为中心的方法可以解决仅利用两个领域的共同特征的以数据为中心方法的问题。
Fernando等人[11]提出了一种以子空间为中心的方法,即子空间对齐(SA)。
SA的关键思想是使用变换矩阵M将源基向量(A)与目标基向量(B)对齐。
然而,在使用线性映射映射源子空间后,由于域偏移,投影源域数据的方差将不同于目标域数据。
在这种情况下,SA在对齐子空间后无法最小化域之间的分布。
此外,SA不能处理两个子空间之间的移位是非线性的情况。
子空间分布对齐(SDA)[14]通过考虑正交主成分的方差来改进SA。然而,方差是基于对齐的子空间来考虑的。因此,仅改变每个本征方向的幅度,当域偏移较大时,该幅度仍可能失败。
图2中的合成数据说明和真实数据集的实验结果证实了这一点
三、联合几何和统计对齐
3.1问题定义
我们从术语的定义开始。源域数据表示为
X
s
∈
R
D
×
n
s
X_s\in\mathbb{R}^{D\times n_s}
Xs∈RD×ns是从分布
P
s
(
X
s
)
P_s(X_s)
Ps(Xs)中得出的;目标域数据表示为
X
t
∈
R
D
×
n
t
X_t\in\mathbb{R}^{D\times n_t}
Xt∈RD×nt是从分布
P
t
(
X
t
)
P_t(X_t)
Pt(Xt)中得出的,其中
D
D
D是数据实例的维数,
n
s
n_s
ns和
n
t
n_t
nt分别是源域和目标域中的样本数。
在无监督域自适应中的训练阶段,有足够的标记源域数据,
D
s
=
{
(
x
i
,
y
i
)
}
i
=
1
n
s
,
x
i
∈
R
D
D_s=\{(x_i,y_i)\}^{n_s}_{i=1},x_i\in\mathbb{R}^D
Ds={(xi,yi)}i=1ns,xi∈RD和有足够的未标记的目标域数据,
D
t
=
{
(
x
j
)
}
j
=
1
n
t
,
x
j
∈
R
D
D_t=\{(x_j)\}^{n_t}_{j=1},x_j\in\mathbb{R}^D
Dt={(xj)}j=1nt,xj∈RD。
我们假设域之间的特征空间和标签空间是相同的:
X
s
=
X
t
X_s=X_t
Xs=Xt和
Y
s
=
Y
t
Y_s=Y_t
Ys=Yt。由于数据集移位,
P
s
(
X
s
)
≠
P
t
(
X
t
)
P_s(X_s)\ne P_t(X_t)
Ps(Xs)=Pt(Xt)
与以前的域适配方法不同,我们不假设存在统一的变换
ϕ
(
⋅
)
\phi(\cdot)
ϕ(⋅),使得
P
s
(
ϕ
(
X
s
)
)
=
P
t
(
ϕ
(
X
t
)
)
和
P
s
(
Y
s
∣
ϕ
(
X
s
)
)
)
=
P
t
(
Y
t
∣
ϕ
(
X
s
)
)
P_s(\phi(X_s))=P_t(\phi(X_t))和P_s(Y_s|\phi(X_s)))=P_t(Y_t|\phi(X_s))
Ps(ϕ(Xs))=Pt(ϕ(Xt))和Ps(Ys∣ϕ(Xs)))=Pt(Yt∣ϕ(Xs)),因为当数据集偏移较大时,此假设无效。
3.2公式化
为了解决以数据为中心和以子空间为中心的方法的局限性,所提出的框架(JGSA)通过利用两个域的共享特征和特定于域的特征,在统计和几何上减少了域差异。
JGSA通过找到两个双投影(A用于源域,B用于目标域)来制定,以获得各个域的新表示,使得
- 目标域的方差最大化,
- 源域的鉴别信息得到预服务,
- 源和目标分布的散度较小,
- 源子空间和目标子空间之间的散度很小。
3.2.1目标方差最大化
为了避免将特征投影到不相关的维度,我们鼓励在相应的子空间中使目标域的方差最大化。因此,方差最大化可以如下实现:
max
B
T
r
(
B
T
S
t
B
)
(1)
\max_BTr(B^TS_tB)\tag{1}
BmaxTr(BTStB)(1)
其中
S
t
=
X
t
H
t
X
t
T
(2)
S_t=X_tH_tX_t^T\tag{2}
St=XtHtXtT(2)
是目标域散度函数,
H
t
=
I
t
−
1
n
t
1
t
1
t
T
H_t=I_t-\frac{1}{n_t}\mathbb{1}_t\mathbb{1}_t^T
Ht=It−nt11t1tT是中心函数。
1
t
∈
R
n
t
1_t\in\mathbb{R}^{n_t}
1t∈Rnt是列向量全为1的矩阵。
3.2.2源鉴别信息保存
由于源域中的标签是可用的,我们可以使用标签信息来约束源域数据的新表示,表示具有区别性。
max
A
t
r
(
A
T
S
b
A
)
(3)
\max_Atr(A^TS_bA)\tag{3}
Amaxtr(ATSbA)(3)
max
A
t
r
(
A
T
S
w
A
)
(4)
\max_Atr(A^TS_wA)\tag{4}
Amaxtr(ATSwA)(4)
其中
S
w
S_w
Sw为源域数据的类内分散矩阵,
S
b
S_b
Sb为源域数据的之间的类间分散矩阵,定义如下:
S
w
=
∑
c
=
1
C
X
s
(
c
)
H
s
(
c
)
(
X
s
(
c
)
)
T
(5)
S_w=\sum^C_{c=1}X_s^{(c)}H_s^{(c)}(X_s^{(c)})^T\tag{5}
Sw=c=1∑CXs(c)Hs(c)(Xs(c))T(5)
S
b
=
∑
c
=
1
C
n
s
(
c
)
(
m
s
(
c
)
−
m
ˉ
s
)
(
m
s
(
c
)
−
m
ˉ
s
)
T
(6)
S_b=\sum^C_{c=1}n_s^{(c)}(m^{(c)}_s-\bar{m}_s)(m^{(c)}_s-\bar{m}_s)^T\tag{6}
Sb=c=1∑Cns(c)(ms(c)−mˉs)(ms(c)−mˉs)T(6)
X
s
(
c
)
∈
R
D
×
n
s
(
c
)
X_s^{(c)}\in\mathbb{R}^{D\times n_s^ {(c)}}
Xs(c)∈RD×ns(c)是一组源样本属于类c,
m
s
(
c
)
=
1
n
s
(
c
)
∑
i
=
1
n
s
(
c
)
x
i
(
c
)
,
m
ˉ
s
=
1
n
s
∑
i
=
1
n
s
x
i
,
H
s
(
c
)
=
I
s
(
c
)
−
1
n
s
(
c
)
1
s
(
c
)
(
1
s
(
c
)
)
T
m_s^{(c)}=\frac{1}{n_s^{(c)}}\sum^{n_s^{(c)}}_{i=1}x_i^{(c)},\bar{m}_s=\frac{1}{n_s}\sum^{n_s}_{i=1}x_i,H_s^{(c)}=I^{(c)}_s-\frac{1}{n_s^{(c)}}1^{(c)}_s(1^{(c)}_s)^T
ms(c)=ns(c)1∑i=1ns(c)xi(c),mˉs=ns1∑i=1nsxi,Hs(c)=Is(c)−ns(c)11s(c)(1s(c))T是类c的中心矩阵,
I
s
(
c
)
∈
R
n
s
(
c
)
×
n
s
(
c
)
I^{(c)}_s\in\mathbb{R}^{ n_s^ {(c)}\times n_s^ {(c)}}
Is(c)∈Rns(c)×ns(c)是单位矩阵,
1
s
(
c
)
∈
R
n
s
(
c
)
1^{(c)}_s\in\mathbb{R}^{ n_s^ {(c)}}
1s(c)∈Rns(c)是全为1的列向量,
n
s
(
c
)
n_s^ {(c)}
ns(c)为c类源样本的数量。
3.2.3分布散度最小化
我们使用MMD标准来比较域之间的距离分布,它计算了k维嵌入中源数据和目标数据的样本均值之间的距离,
min
A
,
B
∥
1
n
s
∑
x
i
∈
X
s
A
T
x
i
−
1
n
t
∑
x
j
∈
X
t
B
T
x
j
∥
F
2
(7)
\min_{A,B}\left\|\frac{1}{n_s}\sum_{x_i\in X_s}A^Tx_i-\frac{1}{n_t}\sum_{x_j\in X_t}B^Tx_j\right\|^2_F\tag{7}
A,Bmin∥
∥ns1xi∈Xs∑ATxi−nt1xj∈Xt∑BTxj∥
∥F2(7)
Long等人[7]提出利用源域分类器预测的目标伪标签来表示目标域中的类条件数据分布。
然后迭代细化目标域的伪标签,进一步减小两个域条件分布的差异。
我们遵循他们的想法,最小化域之间的条件分布转移,
min
A
,
B
∑
c
=
1
C
∥
1
n
s
(
c
)
∑
x
i
∈
X
s
(
c
)
A
T
x
i
−
1
n
t
(
c
)
∑
x
j
∈
X
t
(
c
)
B
T
x
j
∥
F
2
(8)
\min_{A,B}\sum^C_{c=1}\left\|\frac{1}{n_s^{(c)}}\sum_{x_i\in X_s^{(c)}}A^Tx_i-\frac{1}{n_t^{(c)}}\sum_{x_j\in X_t^{(c)}}B^Tx_j\right\|^2_F\tag{8}
A,Bminc=1∑C∥
∥ns(c)1xi∈Xs(c)∑ATxi−nt(c)1xj∈Xt(c)∑BTxj∥
∥F2(8)
因此,结合边际分布偏移和条件分布偏移最小项,最终分布散度最小项可以改写为
min
A
,
B
T
r
(
[
A
T
B
T
]
[
M
s
M
s
t
M
t
s
M
t
]
[
A
B
]
)
(9)
\min_{A,B}Tr(\begin{bmatrix}A^T&B^T\end{bmatrix}\begin{bmatrix}M_s&M_{st}\\M_{ts}&M_t\end{bmatrix}\begin{bmatrix}A\\B\end{bmatrix})\tag{9}
A,BminTr([ATBT][MsMtsMstMt][AB])(9)
M
s
=
X
s
(
L
s
+
∑
c
=
1
C
L
s
(
c
)
)
X
s
T
,
L
s
=
1
n
s
2
1
s
1
s
T
(
L
s
(
c
)
)
i
j
=
{
1
(
n
s
(
c
)
)
2
x
i
,
x
j
∈
X
s
(
c
)
0
otherwise
(10)
\begin{array}{cl} M_{s}=X_{s}\left(L_{s}+\sum_{c=1}^{C} L_{s}^{(c)}\right) X_{s}^{T}, & L_{s}=\frac{1}{n_{s}^{2}} 1_{s} 1_{s}^{T} \\ \left(L_{s}^{(c)}\right)_{i j}= \begin{cases}\frac{1}{\left(n_{s}^{(c)}\right)^{2}} & \mathbf{x}_{i}, \mathbf{x}_{j} \in X_{s}^{(c)} \\ 0 & \text { otherwise }\end{cases} \end{array}\tag{10}
Ms=Xs(Ls+∑c=1CLs(c))XsT,(Ls(c))ij=⎩
⎨
⎧(ns(c))210xi,xj∈Xs(c) otherwise Ls=ns211s1sT(10)
M
t
=
X
t
(
L
t
+
∑
c
=
1
C
L
t
(
c
)
)
X
t
T
,
L
t
=
1
n
t
2
1
t
1
t
T
(
L
t
(
c
)
)
i
j
=
{
1
(
n
t
(
c
)
)
2
x
i
,
x
j
∈
X
t
(
c
)
0
otherwise
(11)
\begin{array}{cl} M_{t}=X_{t}\left(L_{t}+\sum_{c=1}^{C} L_{t}^{(c)}\right) X_{t}^{T}, & L_{t}=\frac{1}{n_{t}^{2}} 1_{t} 1_{t}^{T} \\ \left(L_{t}^{(c)}\right)_{i j}= \begin{cases}\frac{1}{\left(n_{t}^{(c)}\right)^{2}} & \mathbf{x}_{i}, \mathbf{x}_{j} \in X_{t}^{(c)} \\ 0 & \text { otherwise }\end{cases} \end{array}\tag{11}
Mt=Xt(Lt+∑c=1CLt(c))XtT,(Lt(c))ij=⎩
⎨
⎧(nt(c))210xi,xj∈Xt(c) otherwise Lt=nt211t1tT(11)
M
s
t
=
X
s
(
L
s
t
+
∑
c
=
1
C
L
s
t
(
c
)
)
X
t
T
,
L
s
t
=
−
1
n
s
n
t
1
s
1
t
T
(
L
s
t
(
c
)
)
i
j
=
{
−
1
n
s
(
c
)
n
t
(
c
)
x
i
∈
X
s
(
c
)
,
x
j
∈
X
t
(
c
)
0
otherwise
(12)
\begin{array}{cl} M_{st}=X_{s}\left(L_{st}+\sum_{c=1}^{C} L_{st}^{(c)}\right) X_{t}^{T}, & L_{st}=-\frac{1}{n_{s}n_{t}} 1_{s} 1_{t}^{T} \\ \left(L_{st}^{(c)}\right)_{i j}= \begin{cases}-\frac{1}{n_{s}^{(c)}n_{t}^{(c)}} & \mathbf{x}_{i} \in X_{s}^{(c)},\mathbf{x}_{j} \in X_{t}^{(c)} \\ 0 & \text { otherwise }\end{cases} \end{array}\tag{12}
Mst=Xs(Lst+∑c=1CLst(c))XtT,(Lst(c))ij={−ns(c)nt(c)10xi∈Xs(c),xj∈Xt(c) otherwise Lst=−nsnt11s1tT(12)
M
t
s
=
X
t
(
L
t
s
+
∑
c
=
1
C
L
t
s
(
c
)
)
X
s
T
,
L
t
s
=
−
1
n
s
n
t
1
t
1
s
T
(
L
t
s
(
c
)
)
i
j
=
{
−
1
n
s
(
c
)
n
t
(
c
)
x
j
∈
X
s
(
c
)
,
x
i
∈
X
t
(
c
)
0
otherwise
(13)
\begin{array}{cl} M_{ts}=X_{t}\left(L_{ts}+\sum_{c=1}^{C} L_{ts}^{(c)}\right) X_{s}^{T}, & L_{ts}=-\frac{1}{n_{s}n_{t}} 1_{t} 1_{s}^{T} \\ \left(L_{ts}^{(c)}\right)_{i j}= \begin{cases}-\frac{1}{n_{s}^{(c)}n_{t}^{(c)}} & \mathbf{x}_{j} \in X_{s}^{(c)},\mathbf{x}_{i} \in X_{t}^{(c)} \\ 0 & \text { otherwise }\end{cases} \end{array}\tag{13}
Mts=Xt(Lts+∑c=1CLts(c))XsT,(Lts(c))ij={−ns(c)nt(c)10xj∈Xs(c),xi∈Xt(c) otherwise Lts=−nsnt11t1sT(13)
注意,这与TCA和JDA不同,因为我们不使用统一的子空间,因为可能不存在这样一个公共的子空间,其中两个域的分布也是相似的。
3.2.4子空间散度极小化
与SA[11]相似,我们也通过靠近源和目标子空间来减少域之间的差异。
如前所述,将源子空间映射到SA中的目标子空间需要一个额外的变换矩阵M。
然而,我们不学习一个额外的矩阵来映射这两个子空间。
而是同时对A和B进行优化,既保留了源类信息和目标方差,又使两个子空间同时趋近。
我们使用以下术语将两个子空间移动到一起:
min
A
,
B
∥
A
−
B
∥
F
2
(14)
\min_{A,B}\|A-B\|^2_F\tag{14}
A,Bmin∥A−B∥F2(14)
通过将术语(14)和术语(9)结合使用,既利用了共享特征,又利用了领域特定特征,从而使两个领域在几何和统计上良好对齐
3.2.5总体目标函数
我们将上述5个数量((1)、(3)、(4)、(9)、(14))合并,制定JGSA方法如下:
max
μ
{
Target Var.
}
+
β
{
Between Class Var.
}
{
Distribution shift
}
+
λ
{
Subspace shift
}
+
β
{
Within Class Var.
}
\max\frac{\mu\{\text{Target Var.}\}+\beta\{\text{Between Class Var.}\}}{\{\text{Distribution shift}\}+\lambda\{\text{Subspace shift}\}+\beta\{\text{Within Class Var.}\}}
max{Distribution shift}+λ{Subspace shift}+β{Within Class Var.}μ{Target Var.}+β{Between Class Var.}
其中λ、μ、β为权衡参数,以平衡每个量的重要性,Var.表示方差。
我们遵循[9]进一步施加
T
r
(
B
T
B
)
Tr(B^TB)
Tr(BTB)小的约束来控制B的规模,具体来说,我们的目标是通过求解下面的优化函数,找到两个耦合的投影A和B,
max
A
,
B
Tr
(
[
A
T
B
T
]
[
β
S
b
0
0
μ
S
t
]
[
A
B
]
)
Tr
(
[
A
T
B
T
]
[
M
s
+
λ
I
+
β
S
w
M
s
t
−
λ
I
M
t
s
−
λ
I
M
t
+
(
λ
+
μ
)
I
]
[
A
B
]
)
(15)
\max _{A, B} \frac{\operatorname{Tr}\left(\left[\begin{array}{ll} A^{T} & B^{T} \end{array}\right]\left[\begin{array}{cc} \beta S_{b} & \mathbf{0} \\ \mathbf{0} & \mu S_{t} \end{array}\right]\left[\begin{array}{l} A \\ B \end{array}\right]\right)}{\operatorname{Tr}\left(\left[\begin{array}{ll} A^{T} & B^{T} \end{array}\right]\left[\begin{array}{cc} M_{s}+\lambda I+\beta S_{w} & M_{s t}-\lambda I \\ M_{t s}-\lambda I & M_{t}+(\lambda+\mu) I \end{array}\right]\left[\begin{array}{l} A \\ B \end{array}\right]\right)}\tag{15}
A,BmaxTr([ATBT][Ms+λI+βSwMts−λIMst−λIMt+(λ+μ)I][AB])Tr([ATBT][βSb00μSt][AB])(15)
其中
I
∈
R
d
×
d
I\in\mathbb{R}^{d\times d}
I∈Rd×d是单位矩阵
最小化(15)的分母可以使边际分布和条件分布偏移较小,并且源域内的类方差较小。
使(15)的分子最大化会导致目标域方差变大,源域类间方差也变大。
与JDA相似,我们也使用学习到的变换迭代更新目标域数据的伪标签,以提高标签质量,直到收敛。
3.3最优化
为了优化(15),我们将
[
A
T
B
T
]
\begin{bmatrix}A^T&B^T\end{bmatrix}
[ATBT]改写为
W
T
W^T
WT。
则可将目标函数及相应的约束条件改写为:
max
W
Tr
(
W
T
[
β
S
b
0
0
μ
S
t
]
W
)
Tr
(
W
T
[
M
s
+
λ
I
+
β
S
w
M
s
t
−
λ
I
M
t
s
−
λ
I
M
t
+
(
λ
+
μ
)
I
]
W
)
(16)
\max _{W} \frac{\operatorname{Tr}\left(W^T\left[\begin{array}{cc} \beta S_{b} & \mathbf{0} \\ \mathbf{0} & \mu S_{t} \end{array}\right]W\right)}{\operatorname{Tr}\left(W^T\left[\begin{array}{cc} M_{s}+\lambda I+\beta S_{w} & M_{s t}-\lambda I \\ M_{t s}-\lambda I & M_{t}+(\lambda+\mu) I \end{array}\right]W\right)}\tag{16}
WmaxTr(WT[Ms+λI+βSwMts−λIMst−λIMt+(λ+μ)I]W)Tr(WT[βSb00μSt]W)(16)
注意,目标函数对于w的缩放是不变的,因此,我们将目标函数(16)重写为
max
W
Tr
(
W
T
[
β
S
b
0
0
μ
S
t
]
W
)
s
.
t
.
Tr
(
W
T
[
M
s
+
λ
I
+
β
S
w
M
s
t
−
λ
I
M
t
s
−
λ
I
M
t
+
(
λ
+
μ
)
I
]
W
)
=
1
(17)
\max _{W} \operatorname{Tr}\left(W^T\left[\begin{array}{cc} \beta S_{b} & \mathbf{0} \\ \mathbf{0} & \mu S_{t} \end{array}\right]W\right)\tag{17}\\ s.t.\operatorname{Tr}\left(W^T\left[\begin{array}{cc} M_{s}+\lambda I+\beta S_{w} & M_{s t}-\lambda I \\ M_{t s}-\lambda I & M_{t}+(\lambda+\mu) I \end{array}\right]W\right)=1
WmaxTr(WT[βSb00μSt]W)s.t.Tr(WT[Ms+λI+βSwMts−λIMst−λIMt+(λ+μ)I]W)=1(17)
(17)的拉格朗日函数为
L
=
Tr
(
W
T
[
β
S
b
0
0
μ
S
t
]
W
)
+
Tr
(
(
W
T
[
M
s
+
λ
I
+
β
S
w
M
s
t
−
λ
I
M
t
s
−
λ
I
M
t
+
(
λ
+
μ
)
I
]
W
−
I
)
Φ
)
(18)
L=\operatorname{Tr}\left(W^T\left[\begin{array}{cc} \beta S_{b} & \mathbf{0} \\ \mathbf{0} & \mu S_{t} \end{array}\right]W\right)\tag{18}\\ +\operatorname{Tr}\left(\left(W^T\left[\begin{array}{cc} M_{s}+\lambda I+\beta S_{w} & M_{s t}-\lambda I \\ M_{t s}-\lambda I & M_{t}+(\lambda+\mu) I \end{array}\right]W-I\right)\Phi\right)
L=Tr(WT[βSb00μSt]W)+Tr((WT[Ms+λI+βSwMts−λIMst−λIMt+(λ+μ)I]W−I)Φ)(18)
通过
∂
L
∂
W
=
0
\frac{\partial L}{\partial W} = 0
∂W∂L=0,我们得到:
[
β
S
b
0
0
μ
S
t
]
W
=
[
M
s
+
λ
I
+
β
S
w
M
s
t
−
λ
I
M
t
s
−
λ
I
M
t
+
(
λ
+
μ
)
I
]
W
Φ
(19)
\left[\begin{array}{cc} \beta S_{b} & \mathbf{0} \\ \mathbf{0} & \mu S_{t} \end{array}\right]W=\left[\begin{array}{cc} M_{s}+\lambda I+\beta S_{w} & M_{s t}-\lambda I \\ M_{t s}-\lambda I & M_{t}+(\lambda+\mu) I \end{array}\right]W\Phi\tag{19}
[βSb00μSt]W=[Ms+λI+βSwMts−λIMst−λIMt+(λ+μ)I]WΦ(19)
其中
Φ
=
d
i
a
g
(
λ
1
,
…
,
λ
k
)
\Phi= diag(\lambda_1,…, \lambda_k)
Φ=diag(λ1,…,λk)为k个前导特征值,
W
=
[
W
1
,
…
,
W
k
]
W = [W_1,…, W_k]
W=[W1,…,Wk]包含对应的特征向量,可以通过广义特征值分解解析求解。
一旦得到变换矩阵W,就可以很容易地得到子空间A和B。
算法1中总结了JGSA的伪代码。

3.4核化分析
利用一些核函数
ϕ
\phi
ϕ,将JGSA方法推广到可再生核希尔伯特空间(RKHS)中的非线性问题。
我们使用代表定理
P
=
ϕ
(
X
)
A
和
Q
=
ϕ
(
X
)
B
P = \phi(X)A和Q = \phi(X)B
P=ϕ(X)A和Q=ϕ(X)B来核化我们的方法,其中
X
=
[
X
s
,
X
t
]
X = [X_s, X_t]
X=[Xs,Xt]表示所有源和目标训练样本,
Φ
(
X
)
=
[
ϕ
(
x
1
)
,
…
,
ϕ
(
x
n
)
]
\Phi(X) = [\phi(x_1),…, \phi(x_n)]
Φ(X)=[ϕ(x1),…,ϕ(xn)], n为所有样本个数。
因此,目标函数为:
max
P
,
Q
Tr
(
[
P
T
Q
T
]
[
β
S
b
0
0
μ
S
t
]
[
P
Q
]
)
Tr
(
[
P
T
Q
T
]
[
M
s
+
λ
I
+
β
S
w
M
s
t
−
λ
I
M
t
s
−
λ
I
M
t
+
(
λ
+
μ
)
I
]
[
P
Q
]
)
(20)
\max _{P, Q} \frac{\operatorname{Tr}\left(\left[\begin{array}{ll} P^{T} & Q^{T} \end{array}\right]\left[\begin{array}{cc} \beta S_{b} & \mathbf{0} \\ \mathbf{0} & \mu S_{t} \end{array}\right]\left[\begin{array}{l} P \\ Q \end{array}\right]\right)}{\operatorname{Tr}\left(\left[\begin{array}{ll} P^{T} & Q^{T} \end{array}\right]\left[\begin{array}{cc} M_{s}+\lambda I+\beta S_{w} & M_{s t}-\lambda I \\ M_{t s}-\lambda I & M_{t}+(\lambda+\mu) I \end{array}\right]\left[\begin{array}{l} P \\ Q \end{array}\right]\right)}\tag{20}
P,QmaxTr([PTQT][Ms+λI+βSwMts−λIMst−λIMt+(λ+μ)I][PQ])Tr([PTQT][βSb00μSt][PQ])(20)
在内核版本中,所有的
X
t
X_t
Xt都被
Φ
(
X
t
)
\Phi(X_t)
Φ(Xt)取代,所有的
X
s
X_s
Xs都被
Φ
(
X
s
)
\Phi(X_s)
Φ(Xs)取代,包括
S
t
、
S
w
、
S
b
、
M
s
、
M
t
、
M
s
t
和
M
t
s
S_t、S_w、S_b、M_s、M_t、M_{st}和M_{ts}
St、Sw、Sb、Ms、Mt、Mst和Mts。
我们用
Φ
(
X
)
A
\Phi(X)A
Φ(X)A和
Φ
(
X
)
B
\Phi(X)B
Φ(X)B替换P和Q,得到的目标函数如下:
max
A
,
B
Tr
(
[
A
T
B
T
]
[
β
S
b
0
0
μ
S
t
]
[
A
B
]
)
Tr
(
[
A
T
B
T
]
[
M
s
+
λ
K
+
β
S
w
M
s
t
−
λ
K
M
t
s
−
λ
K
M
t
+
(
λ
+
μ
)
K
]
[
A
B
]
)
(21)
\max _{A, B} \frac{\operatorname{Tr}\left(\left[\begin{array}{ll} A^{T} & B^{T} \end{array}\right]\left[\begin{array}{cc} \beta S_{b} & \mathbf{0} \\ \mathbf{0} & \mu S_{t} \end{array}\right]\left[\begin{array}{l} A \\ B \end{array}\right]\right)}{\operatorname{Tr}\left(\left[\begin{array}{ll} A^{T} & B^{T} \end{array}\right]\left[\begin{array}{cc} M_{s}+\lambda K+\beta S_{w} & M_{s t}-\lambda K \\ M_{t s}-\lambda K & M_{t}+(\lambda+\mu) K \end{array}\right]\left[\begin{array}{l} A \\ B \end{array}\right]\right)}\tag{21}
A,BmaxTr([ATBT][Ms+λK+βSwMts−λKMst−λKMt+(λ+μ)K][AB])Tr([ATBT][βSb00μSt][AB])(21)
其中
S
t
=
K
~
t
K
~
t
T
,
S
w
=
K
s
H
s
(
c
)
K
s
T
,
K
=
Φ
(
X
)
T
Φ
(
X
)
,
K
s
=
Φ
(
X
)
T
Φ
(
X
s
)
,
K
t
=
Φ
(
X
)
T
Φ
(
X
t
)
,
K
~
t
=
K
t
−
1
t
K
−
K
t
1
n
+
1
t
K
1
n
,
1
t
∈
R
n
t
×
n
S_t=\tilde K_t\tilde K_t^T,S_w=K_sH_s^{(c)}K_s^T,K=\Phi(X)^T\Phi(X),K_s=\Phi(X)^T\Phi(X_s),K_t=\Phi(X)^T\Phi(X_t),\tilde K_t=K_t-1_tK-K_t1_n+1_tK1_n,1_t\in\mathbb{R}^{n_t\times n}
St=K~tK~tT,Sw=KsHs(c)KsT,K=Φ(X)TΦ(X),Ks=Φ(X)TΦ(Xs),Kt=Φ(X)TΦ(Xt),K~t=Kt−1tK−Kt1n+1tK1n,1t∈Rnt×n和
1
n
∈
R
n
×
n
1_n\in\mathbb{R}^{n\times n}
1n∈Rn×n是全为
1
n
\frac{1}{n}
n1的矩阵。
S
b
,
m
s
(
c
)
=
1
n
s
(
c
)
∑
i
=
1
n
s
(
c
)
k
i
(
c
)
,
m
ˉ
s
=
1
n
s
∑
i
=
1
n
s
k
i
,
k
i
=
Φ
(
X
)
T
ϕ
(
x
i
)
S_b,m_s^{(c)}=\frac{1}{n_s^{(c)}}\sum^{n_s^{(c)}}_{i=1}k_i^{(c)},\bar m_s=\frac{1}{n_s}\sum^{n_s}_{i=1}k_i,k_i=\Phi(X)^T\phi(x_i)
Sb,ms(c)=ns(c)1∑i=1ns(c)ki(c),mˉs=ns1∑i=1nski,ki=Φ(X)Tϕ(xi)
在MMD术语中
M
s
=
K
s
(
L
s
+
∑
c
=
1
C
L
s
(
c
)
)
K
s
T
,
M
t
=
K
t
(
L
t
+
∑
c
=
1
C
L
t
(
c
)
)
K
t
T
,
M
s
t
=
K
s
(
L
s
t
+
∑
c
=
1
C
L
s
t
(
c
)
)
K
t
T
,
M
t
s
=
K
t
(
L
t
s
+
∑
c
=
1
C
L
t
s
(
c
)
)
K
s
T
M_{s}=K_{s}\left(L_{s}+\sum_{c=1}^{C} L_{s}^{(c)}\right) K_{s}^{T},M_{t}=K_{t}\left(L_{t}+\sum_{c=1}^{C} L_{t}^{(c)}\right) K_{t}^{T},M_{st}=K_{s}\left(L_{st}+\sum_{c=1}^{C} L_{st}^{(c)}\right) K_{t}^{T},M_{ts}=K_{t}\left(L_{ts}+\sum_{c=1}^{C} L_{ts}^{(c)}\right) K_{s}^{T}
Ms=Ks(Ls+∑c=1CLs(c))KsT,Mt=Kt(Lt+∑c=1CLt(c))KtT,Mst=Ks(Lst+∑c=1CLst(c))KtT,Mts=Kt(Lts+∑c=1CLts(c))KsT
一旦获得核化目标函数(21),我们可以用与原始目标函数相同的方法简单地求解它,以计算A和B。
四、实验
我们将我们的方法与几种最先进的方法进行比较:子空间对齐(SA)[11]、子空间分布对齐(SDA)[14]、测地线流核(GFK)[10]、传输分量分析(TCA)[6]、联合分布分析(JDA)[7]、传输联合匹配(TJM)[8]、散射分量分析(SCA)[9]、最优传输(OTGL)[15]和核流形对齐(KEMA)[16]。对于所有基线方法,我们使用原始论文推荐的参数。
对于JGSA,我们在所有实验中都将
λ
=
1
,
μ
=
1
\lambda=1,\mu=1
λ=1,μ=1固定,因此分布偏移、子空间偏移和目标方差被视为同等重要。我们通过实验验证了固定参数可以在不同类型的任务中获得有希望的结果。因此,子空间维数
k
k
k、迭代次数
T
T
T和正则化参数
β
\beta
β是自由参数。
4.1合成数据
合成的源域和目标域样本均来自三个RBF分布的混合。
全局均值以及第三类均值在域之间移动。原始数据是三维的。对于所有方法,我们将子空间的维数设置为2。

4.2真实世界数据集
我们在三个跨域虚拟识别任务中评估了我们的方法:对象识别(Office,Caltech256)、手写数字识别(USPS,MNIST)和基于RGB-D的动作识别(MSRAction3DExt、G3D、UTD-MHAD和MAD)。示例图像或视频帧如图1所示
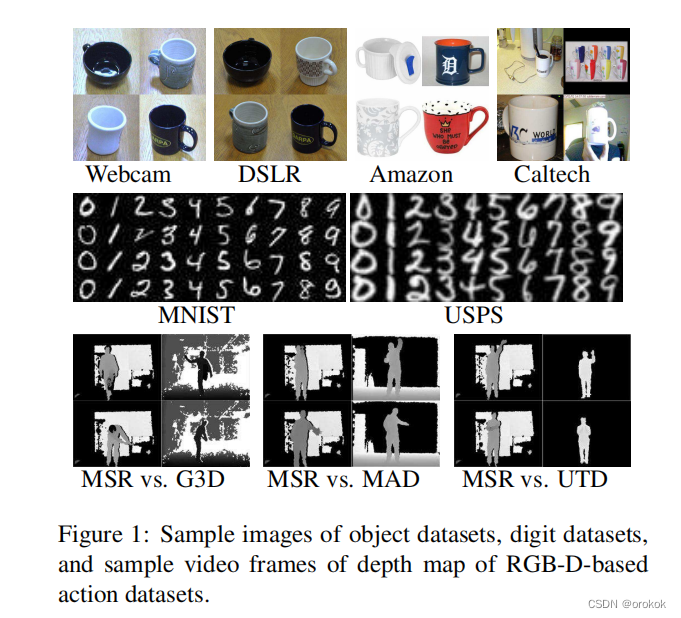
4.2.1设置
物体识别:
我们考虑了两种类型的特征:SURF描述符(使用800个二进制直方图进行编码,代码本从Amazon图像子集中进行训练)和Decaf6特征(在imageNet上训练的卷积网络的第六个完全连接层的激活)。
如[10]所述,选择1-最近邻分类器(NN)作为基础分类器。对于自由参数,我们设置
k
=
30
,
T
=
10
,
β
=
0.1
k=30,T=10,\beta=0.1
k=30,T=10,β=0.1。
数字识别:
所有图像都被均匀地重新缩放到
16
×
16
16\times 16
16×16的大小,并且每个图像由编码灰度像素值的特征向量表示。对于自由参数,我们设置
k
=
100
,
T
=
10
,
β
=
0.01
k=100,T=10,\beta=0.01
k=100,T=10,β=0.01。
基于RGB-D的动作识别:
对于自由参数,我们设置
k
=
100
和
β
=
0.01
k=100和\beta=0.01
k=100和β=0.01。
为了避免过度拟合目标训练集,我们在动作识别任务中设置
T
=
1
T=1
T=1
4.2.2结果和讨论
表1、表2和表3显示了三种真实世界跨域(对象、数字和动作)数据集的结果。


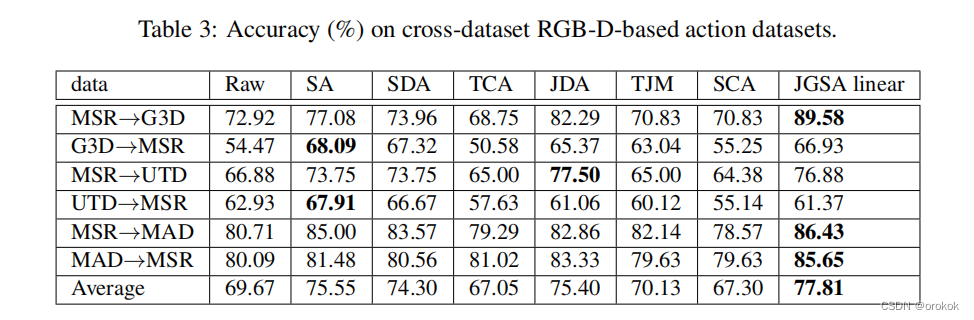
JGSA原始表示原始数据空间上JGSA方法的结果,而JGSA线性和JGSA RBF分别表示线性核和RBF核的结果。
我们还评估了跨域对象数据集(带线性内核的SURF)的运行时复杂性。平均运行时间为28.97秒,大约是最佳基线方法(JDA)的三倍。这是因为JGSA同时学习两个映射,与JDA相比,特征分解矩阵的大小增加了一倍。
4.2.3参数灵敏度
不同类型数据集的结果表明,固定
λ
=
1
和µ
=
1
λ=1和µ=1
λ=1和µ=1足以完成所有三项任务。因此,我们只评估其他三个参数
(
k
、
β
和
T
)
(k、β和T)
(k、β和T)。
我们在USPS上进行实验→MNIST,W→A(具有线性核SURF descriptor)和MSR→MAD数据集用于说明,如图3所示。
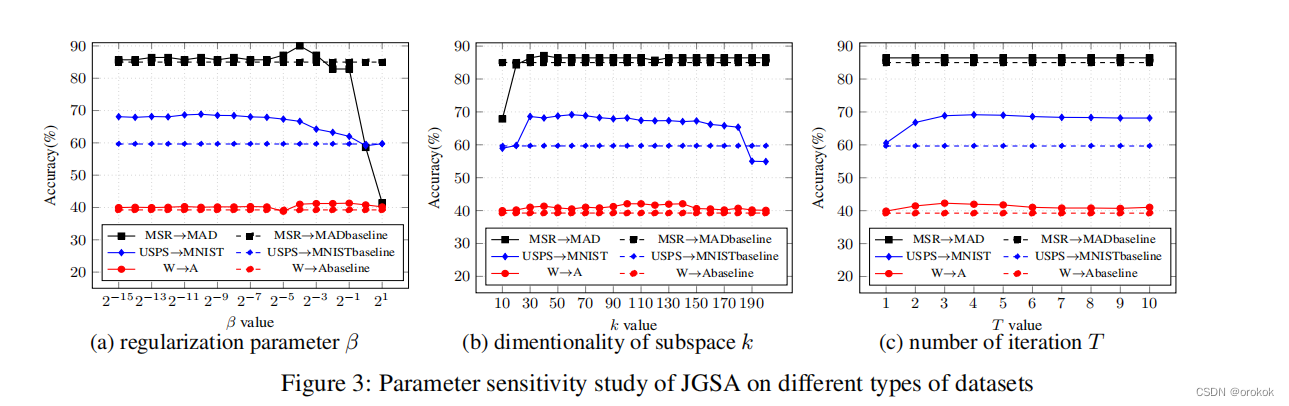
实线是使用不同参数的JGSA的精度,虚线表示通过每个数据集的最佳基线方法获得的结果。在其他数据集上也观察到类似的趋势。
五、总结
在本文中,我们提出了一种新的无监督域自适应框架,称为联合几何和统计对齐(JGSA)。JGSA通过考虑源域和目标域数据的几何和统计特性,并利用共享和特定域的特征,减少了域偏移。
对合成数据和三种不同类型的真实世界视觉识别任务的综合实验验证了JGSA与几种最先进的领域自适应方法相比的有效性。
Reference
Joint Geometrical and Statistical Alignment for Visual Domain Adaptation





















 902
902











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








