启发式搜索(Informed Search)-贪婪算法GBS+A*算法

最新推荐文章于 2025-03-17 22:52:04 发布
最新推荐文章于 2025-03-17 22:52:04 发布
阅读量1.1w 收藏 93
点赞数 21
分类专栏： 高级人工智能（国科大课程）
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/Suyebiubiu/article/details/101208545
版权

目录

 

写在前面

一、启发式搜索和启发式函数

二、贪婪算法（贪婪最佳优先搜索）greedy best-first search （GBS）

三、A*搜索（结合UCS和GBS）

A*搜索算法结束的条件是什么？

​怎么判证明A* 树搜索的最优性？（这个容易出证明题）

四、怎么选择一个好的启发式函数

​

写在前面

        我们之前几篇博客都是在讨论无信息搜索，包括深度优先、广度优先、代价一致等。我们这个内容主要讨论什么是启发式搜索和启发式函数，介绍两个比较常见的贪婪算法和A*搜索算法。并且告诉大家怎么才可以选择一个更好的启发式函数。最后是图搜索中的应用部分。 

一、启发式搜索和启发式函数

        百科：启发式搜索(Heuristically Search)又称为有信息搜索(Informed Search)，它是利用问题拥有的启发信息来引导搜索，达到减少搜索范围、降低问题复杂度的目的，这种利用启发信息的搜索过程称为启发式搜索。

        启发式搜索的节点一般是基于f(n)来进行扩展的，我们如果了解无信息搜索中代价一致算法（UCS）的话，UCS中也有一个g(n)。启发式搜索中是通过f(n)被选择性扩展（一般使用优先队列），一致代价搜索中使用g(n)来选择性扩展（也是优先队列）。但是启发式搜索中f(n)含义要比g(n)丰富，g(n)仅仅表示从当前节点到下一个节点的开销，但是f(n)可以表示从当前节点到目标节点的估计。

启发式函数（对于大多数最佳优先搜索）：h(n)=节点n到目标节点的最小代价路径的代价估计值
启发式搜索：采用了f(n)（即启发式函数）的搜索策略。

二、贪婪算法（贪婪最佳优先搜索）greedy best-first search （GBS）

        贪婪算法的设计目的就是想要从当前节点扩展离目标节点最近的一个节点。这个算法只用到了最简单的启发式函数f(n)=h(n)，在罗马尼亚问题中，使用的是当前地点到目的地的直线距离（这个信息不能由问题本身的描述计算得到，而且这个信息是有用的——因为和实际路程相关，所以是一个有用的启发式），在此问题中，GBS搜索代价最小，但是不是最优。

GBS可能陷入死循环，但是它在有限状态空间的图搜索下是完备的，其他情况则不是。其时间和空间复杂度都是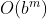O(b^m)，其中m是搜索空间的最大深度。

三、A*搜索（结合UCS和GBS）

A*搜索不同于贪婪算法，贪婪算法仅仅利用了启发式函数h(x)，A*算法结合了代价一致算法UCS和贪婪算法的优点。A*算法可以看到到达此节点已经花费的代价（  g(x) ），A*搜索的启发式函数变为了f(n)=g(n)+h(n)。整体来说，A*算法既是完备的也是最优的。

那么我们可以探讨下，代价一致搜索和A*搜索有啥区别呢？我们通过观察下图可以看出，代价一致搜索在所有方向上是等可能的扩展，而A*搜索方式主要是朝着目标扩展，而且可以保证最优性。启发函数越接近真实的耗散，将扩展越少的节点，但通常会在每个节点计算启发函数本身时有更多的计算。

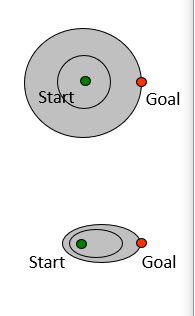
A*搜索算法结束的条件是什么？

怎么判证明A* 树搜索的最优性？（这个容易出证明题）

四、怎么选择一个好的启发式函数

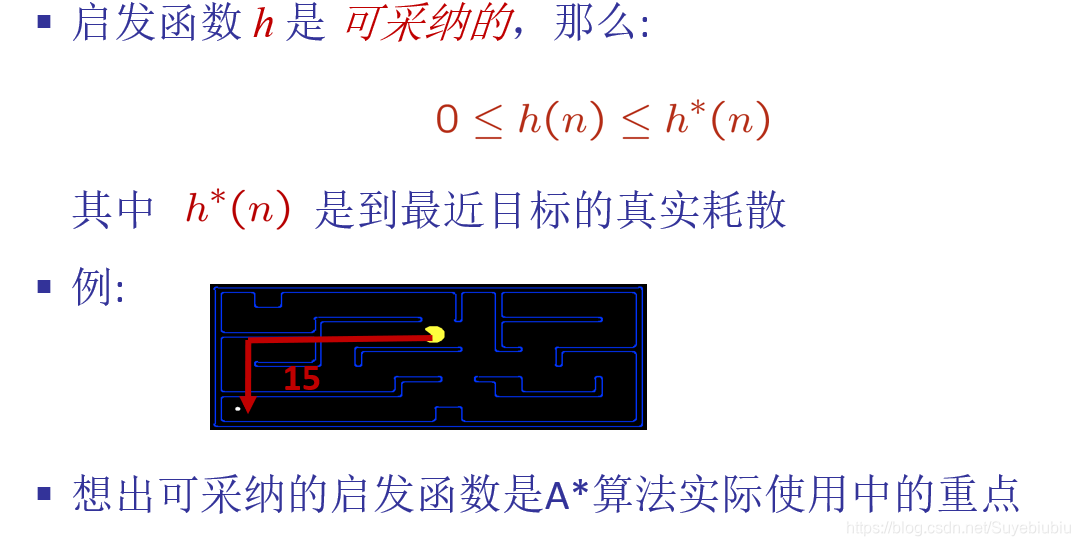
其实我们最大问题并不是理解启发式函数，而是怎么去想出最好的可采纳的启发函数。通常情况下可采纳启发函数都是松弛问题的解的耗散问题。其实不能被采纳的启发函数也不是一无是处，常常也是非常有用的。

优势可以直接转化为效率：使用ha的A*算法绝不会比使用hc扩展更多的节点。

论证：每个f(n)<C*的节点都会被扩展，那么h(n)<C*-g(n)的节点必将被扩展。ha>=hc，那么每个被使用ha的A*算法扩展的节点必定也会被使用hc的A*所扩展，而hc还可能引起其他节点的扩展。

因此，使用值更高的启发函数总是更好的。前提可采纳的启发函数

 

 

基于改进Informed-RRT*的路径规划算法
罗伯特技术屋
07-28 1019
针对Informed-RRT*算法在路径规划中存在盲目性、收敛速度慢和优化效率低等问题，提出了一种改进的Informed-RRT*算法。首先，寻找初始路径时引入双向贪婪搜索，加快了初始路径寻找速率；其次，在树的生长过程中引入自适应步长代替固定步长进行生长，使得算法面对不同环境都能找到较优路径；最后，用懒惰采样代替原本的随机采样，在对算法进行处理前删除没有作用的节点，减小了算法运行压力，也加速了算法收敛。实验结果表明，面对复杂环境，优化后的算法能够快速找到较优路径。
启发式搜索算法
Pbw_666的博客
08-24 3646
模拟退火：   算法步骤：给出初始温度，初始解，退火系数等参数。在温度没有达到降到最终设定的温度时，进行退火过程即进行循环迭代。在该温度下，产生新解，并计算目标函数值。如果目标函数值更优，接受新解。否则，会以一定的概率接受错误解。该过程完成，即完成一次退火。算法的核心，在与接受概率的设定。 内容代补充~ ...
TSP-贪心启发式算法求解
cc098818的博客
08-20 3456
1、贪心算法 （1）概念 贪心算法（贪婪算法），是求解最优化问题常见的简单、迅速的算法，它只是做出在当前看来最好的选择，而不可考虑整体 （2）思路 第一步：描述问题和建立数学模型 第二步：把原问题分解成若干个子问题 第三步：对每个子问题进行求解，得到子问题的局部最优解 第四步：把子问题的局部最优解合并成原问题的解 （3）缺点 求的的解可能与原问题的最优解相差较大 2、贪心算法求解TSP 本文用的算...
经典算法研究系列：八、再谈启发式搜索算法
热门推荐
结构之法 算法之道
02-10 3万+
经典算法研究系列：八、再谈启发式搜索算法作者:July   二零一一年二月十日本文参考：I、  维基百科、II、 人工智能-09 启发式搜索、III、本BLOG内，经典算法研究系列：一、A*搜索算法----------------------------引言：A*搜索算法，作为经典算法研究系列的开篇文章，之前已在本BLOG内有所阐述。但要真正理解A*搜索算法，还是得先从启发式搜索算法谈起。毕竟，A*搜索算法也是启发式算法中的一种。ok，切入正题。一、何谓启发式搜索启发式搜索算法有点像广度优先搜索，不同的是，
L4.1Informed Search
m0_74331272的博客
03-17 1180
在人工智能的搜索算法中，启发式搜索（Informed Search）是相对于无信息搜索（Uninformed Search）的一种改进方法。它利用问题的。
启发式搜索
weixin_30340819的博客
06-12 300
启发式搜索 启发式搜索就是在状态空间中的搜索对每一个搜索的位置进行评估，得到最好的位置，再从这个位置进行搜索直到目标。这样可以省略大量无谓的搜索路径，提高了效率。在启发式搜索中，对位置的估价是十分重要的。采用了不同的估价可以有不同的效果。 在启发式搜索中，我们每次找到当前“最有希望是最短路径”的状态进行扩展。对于每个状态的我们用函数F来估计它是否有希望。F包含两个部分： F = G + ...
A* 算法（启发式搜索）
Rp的博客
02-12 2724
A* 算法 百度百科： A*算法，A*（A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法，也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近，最终搜索速度越快。 别称： 别称：启发式搜索 表达式: f(n)=g(n)+h(n)f(n)=g(n)+h(n)f(n)=g(n)+h(n) 原理 公式表示为： f(n)=g(n)+h(n)f(n)=g(n)+h(n)f(n)...
启发式搜索 (Heuristically Search)-【贪婪最佳优先搜索】和【A*搜索】
小小何先生的学习之旅
02-22 1万+
  搜索是人工智能里面研究的一个核心问题，像强化学习其本质我也是理解为一种搜索算法，不过其用了一些值函数近似的方法，并做了进一步改良，使其功能更加强大。近些年来也有非常多学术研究者慢慢开始将两者融汇贯通发顶会了。比如像Goog的planet，Muzero以及将熵用于蒙特卡洛树搜索中平衡探索和利用的关系等等。 启发式搜索   启发式搜索(Heuristically Search)又称为有信息搜索(I...
rrt算法的matlab代码-ENPM661-Informed-RRT-Star:该存储库包含基于采样的算法RRT、RRT*和Informed
06-07
rrt算法的matlab代码ENPM661-Informed-RRT-Star 该存储库包含基于采样的算法 RRT、RRT* 和 Informed RRT* 的 MATLAB 代码。 该项目是马里兰大学 2018 年Spring学期 ENPM661 自主机器人规划课程的一部分。 RRT算法 ...
机器人轨迹规划RRT-RRPstar-informed RRPstar-PRM算法python代码
03-13
在机器人路径规划领域，RRT（ Rapidly-exploring Random Trees）算法是一种广泛应用的搜索算法，它能够在复杂的环境中快速寻找机器人从起点到终点的有效路径。RRT算法的主要思想是通过随机生成树节点并逐步扩展来...
机器人路径规划中informed-RRT*算法的MATLAB实现及其优化策略
最新发布
04-26
内容概要：本文详细介绍了RRT家族中的informed-RRT*算法，这是一种用于机器人路径规划的全局最优轨迹规划算法。文中首先概述了RRT家族的基本成员如RRT、RRT-Connect和RRT*，然后重点讲解了informed-RRT*的工作原理，...
matlab实现三维informed-RRT*算法代码（有详细注释）
05-06
Informed RRT* 算法的核心在于使用一个可接受的椭圆启发式（admissible ellipsoidal heuristic）来指导搜索过程，从而提高算法的效率和解的质量。 #### a. 椭圆启发式 椭圆启发式定义了一个状态空间的子集，这个...
关于启发式搜索算法
weixin_43389824的博客
11-12 7459
启发式搜索（Informed Search / Heuristic Search） 启发式搜索就是利用启发性信息进行制导的搜索。 启发性信息就是有利于尽快找到问题之解的信息。 按其用途划分，启发性信息一般可分为以下三类： (1)用于扩展节点的选择，即用于决定应先扩展哪一个节点，以免盲目扩展。 (2)用于生成节点的选择，即用于决定应生成哪些后续节点，以免盲目地生成过多无用节点。 (3)用于删除节点的...
算法——启发式搜索
m0_60697583的博客
04-16 1383
通过设计适当的启发式函数，可以在大规模的搜索空间中快速找到接近最优解的解决方案。启发式搜索是一类基于估计值（启发式函数）来指导搜索的算法，常见的有 A* 算法。：启发式搜索在游戏博弈中有着广泛的应用，例如在国际象棋、围棋、扑克等游戏中。其原理是在搜索过程中，不仅仅考虑当前的搜索状态，还利用一定的启发式信息来指导搜索方向，从而更加高效地达到目标状态。：启发式搜索还可以用于智能体的决策问题，例如在强化学习中，智能体可以使用启发式搜索来选择动作以最大化累积奖励。
【人工智能】1.问题求解：启发式搜索算法
深思深练 厚积薄发
11-04 7332
A* 算法是启发式搜索算法中的经典，经常应用于路径搜索和规划中。这里以八数码问题状态空间图的搜索为例，初步介绍以A*算法为代表的启发式搜索。 # 一、启发性信息和估价函数 ## 1.启发性信息： 启发式搜索是利用知识来引导搜索过程的，达到减少搜索范围的目标，使得尽量先走“最有希望的方向”，从而降低问题复杂度。**这里就是要根据知识，设计启发性信息（启发函数）**，启发性信息可以： 1）帮助确定扩展节点的信息 2）有效地帮助决定哪些后继节点应被生成 3）能决定在扩展一个节点时哪些节点应从搜索树上被删除 启发性
人工智能--贪婪算法（启发式搜索）
qq_14843167的博客
07-06 1万+
贪婪算法是启发式算法的代表算法之一，其核心思想是每次都选择局部最优解，但该算法并不能保证最后得出的结果是全局最优解。贪婪算法比较典型的案例就是最短路径搜索。之前，大部分的贪婪算法都是基于图的方式寻找最优路径。本篇文章主要借助路径动态规划的案例利用贪婪算法讲解树的最优路径。 相对于图来说，在树的搜索过程中，贪婪算法会遇到很多不可行解，这就需要程序能否返回到最近的一个节点，重新寻找其他的可行路径。下面通过一个示例说明贪婪最佳优先搜索和改进贪婪优化算法具体过程。 问题描述 下图展示了城市之间的路径图，该图包含了城
informed-rrt* 算法
01-20
### Informed-RRT*算法概述 Informed-RRT*是一种用于路径规划的采样基优化算法，它改进了传统的RRT*(Rapidly-exploring Random Tree Star)方法，在探索空间的同时能够更高效地找到最优解。该算法通过构建一个树结构来表示已访问过的状态，并不断更新这棵树以逼近全局最优路径[^1]。 #### 算法特点 - **启发式搜索范围**：不同于标准RRT*, Informed-RRT*利用椭圆约束缩小可能包含最短路径的空间区域，从而减少不必要的样本点生成。 - **渐近收敛性**：随着迭代次数增加，所得到的最佳路径长度逐渐接近理论上的最小值。 - **计算效率高**：由于采用了更为精确的目标导向策略，因此能够在较短时间内获得高质量的结果。 ```python import numpy as np from scipy.spatial import KDTree class Node: def __init__(self, position): self.position = position self.parent = None self.cost = 0.0 def distance(node1, node2): return np.linalg.norm(np.array(node1.position)-np.array(node2.position)) def steer(from_node, to_position, extend_length=float("inf")): new_node = Node(to_position) d = distance(from_node, new_node) if d > extend_length: ratio = extend_length / d new_node.position = tuple((np.array(from_node.position)+ratio*np.subtract(new_node.position, from_node.position)).tolist()) new_node.parent = from_node new_node.cost = from_node.cost + distance(from_node, new_node) return new_node def informed_rrt_star(start, goal, obstacle_list, rand_area, max_iter=200, expand_dis=1.0, path_resolution=0.5): start_node = Node(start) end_node = Node(goal) tree = {start_node} kd_tree = KDTree([node.position for node in tree]) best_cost = float('inf') final_path = [] for i in range(max_iter): rnd_node = sample_free_space(rand_area) nearest_ind = kd_tree.query(rnd_node.position)[1] nearest_node = list(tree)[nearest_ind] new_node = steer(nearest_node, rnd_node.position, expand_dis) if check_collision(new_node, obstacle_list): continue near_nodes = find_near_nodes(new_node, tree, kd_tree) new_node = choose_parent(new_node, near_nodes) tree.add(new_node) kd_tree = KDTree([node.position for node in tree]) rewire(new_node, near_nodes) if is_within_ellipse(new_node, start_node, end_node): temp_end_node = steer(new_node, end_node.position) if not check_collision(temp_end_node, obstacle_list): current_best_cost = calculate_total_cost(temp_end_node) if current_best_cost < best_cost: best_cost = current_best_cost final_path = get_final_course(temp_end_node) return final_path ```
评论 3
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值