定点数与浮点数

最新推荐文章于 2025-08-22 19:33:50 发布

原创最新推荐文章于 2025-08-22 19:33:50 发布 · 1.4k 阅读

13 ·

CC 4.0 BY-SA版权

文章标签：

#数据库 #fpga开发

计算机的计算从来不是简单的事情，我们将各种数值与码制的转换是为了更加高效方便的运算。

除去最简单的二进制码（也就是原码），我们引入补码的概念。

这是用十进制来解释补码的存在，补码的最大作用就是将一个纯粹的减法转换位一个更加简单方便的加法。借助这个想法，我们发明了二补码，如下表所示

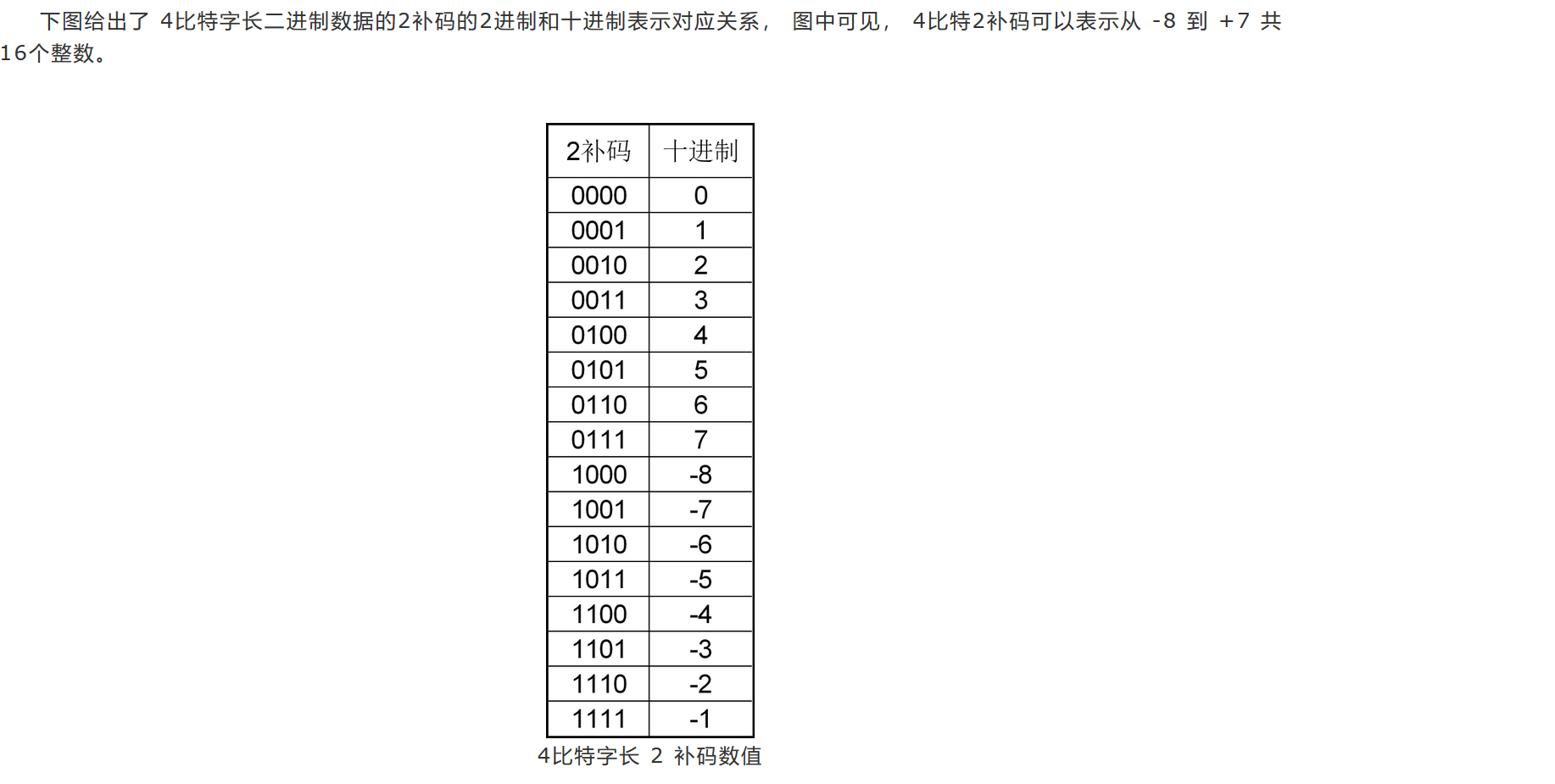
我们可以注意到二补码的最高位是符号位“0”代表整数，“1”代表负数，低三位代表了大小。再正数范围内，数据位和我们所理解的原码相同，但是来到负数的范围的时候，情况就完全不一样了，实际上负数的数据位可以有很方便的计算法则。具体是这样的，将负数的相反数（正数）的数据为按位取反再加上1就能够得到这个负数的数据位了。（注意，使用二补码进行的四则运算的结果也都是二补码），然后二补码得到其真值，若为整数就是读数据位就行了，对于负数的结果，如果不去背表的话，那么其真实值应该是其数据位减1再取反。

值得注意的是， 2补码格式还有一个优良的累加溢出性质：当多个2补码数据相加时，如果加法的中间结果溢出，但是如果理论上的最终结果是不溢出的，则2补码数的加法结果也不会溢出。举例如下：

在4比特字长，2补码格式，计算 -3 -9 + 5
利用上面结果， -3-9 得到 4比特的 7，即0111
4比特字长，5的2补码为 0101，再加上7， 0101+0111 = 1100 ，即4比特字长中，2补码的 -4

以上这种累加溢出特性，在进行信号处理和数值分析等科学计算任务时非常有用，可以先通过理论分析出计算结果的最大字长，然后以之作为累加器字长，对于大规模计算任务能够节省资源提高效率。

也就是中间的溢出和最终结果无关。

浮点数与定点数

可以看出浮点数是被拆分成三部分，最后通过特定的计算来求出最终值。整个数据字长被分为符号位、指数、小数（尾数）三部分。其中，尾数被折算为一个介于1和2之间的数据，然后根据折算出来的指数再确定小数点的位置。由于小数点的位置是随着数据内容动态确定的，浮点数也因此而得名。浮点数的优点是能够有效的利用数据字长，由于采用了指数方法，这种格式能够有效的表示较大和较小的数值。

浮点数的相乘是较为简单的，就是各指数进行相加然后尾数进行相乘。

当来到浮点数相加的时候，就要先进行小数对齐才能够进行加法

十进制定点小数

进行算法的时候，输入计算机的数实际上并不是小数，只有程序员知道这是个小数，并且对其进行处理。并且他是通过小数点的位置进行划分的，也就是以小数点的位置决定谁是整数谁是小数，比较符合直觉。

这一部分缺陷会在后续进行算法的时候进行补偿

有关浮点数与定点数的相互转换：

首先，我们需要知道Qm.n这个定点数的格式，其中m代表m位用于表示整数（含符号），n位用于表示小数。（m好像跟转换没有什么直接的关系）

有一个关键概念就是定标因子，其大小位2^n，我们这边用Scale表示。

然后还有一个概念就是饱和值，当浮点数转换为定点数的时候，有一个范围，大小是

[2^(N-1)，2^(N-1)-1]。

比较中要的概念讲解完了就到了实操环节，我们注意看步骤

例：使用Q1.7的方式转换 float = 0.6548

确定定标因子：Scale = 2^7

缩放：Scale * float = 83.8114(非整数，进行量化（Quantize）)

量化：ceil(向上取整),floor（向下取整）,round（四舍五入），这边使用floor，得83

饱和（Saturate）：83并未超出范围

反向过来转换

直接使用定点值除以一个定标因子Scale，83/2^7 = 0.6484375

定点数的加法：

直接将转化过来的两个数相加就完事了实际上，保证最后的小数位数相同即可

定点数乘法：

将转化之后的定点数进行相乘，然后要更具定标因子Scale将结果除以Scale来调整小数位置。这时就得到了结果的定点数，再/scale就是浮点数了。

下面是用于验证浮点数转化为定点数进行运算，并且计算误差的示例代码

#include <stdio.h>

#define FL  7 // fraction length 
#define SCALE_FL     (1<<7)
#define SCALE_FL_2   (1<<(FL*2))
mult_test(){//浮点数转换位定点数进行乘法 

  float a_f, a_q; char  a_i;
  float b_f, b_q; char  b_i;
  float c_f, c_q; short c_i;

  a_f =  -0.999 ;
  b_f =   0.999 ;
  a_i = a_f * SCALE_FL ;    // fixed point value, S1I0F7
  b_i = b_f * SCALE_FL ;
  a_q = a_i *1.0/ SCALE_FL ;    // quant value
  b_q = b_i *1.0/ SCALE_FL ;

  c_i = a_i * b_i;
  c_q = c_i*1.0 / SCALE_FL_2;//定点数相乘之后，再进行移位去除小数的干扰，再除以定标因子 
  c_f = a_f * b_f;


  printf("# Mult Test\n");
  printf("# Data Quant Fraction length is %d bit\n", FL);
  printf("# a_f =  %-10f, a_i = %-8d 0x%-8x , a_q = %f\n", a_f, a_i, a_i, a_q);
  printf("# b_f =  %-10f, b_i = %-8d 0x%-8x , b_q = %f\n", b_f, b_i, b_i, b_q);
  printf("# c_f =  %-10f, c_i = %-8d 0x%-8x , c_q = %f\n", c_f, c_i, c_i, c_q);
  printf("#\n");

}
add_test(){//测试加法 

  float a_f, a_q; char  a_i;
  float b_f, b_q; char  b_i;
  float c_f, c_q; short c_i;

  a_f =  -0.999 ;
  b_f =  -0.999 ;
  a_i = a_f * SCALE_FL;    // fixed point value, S1I0F7
  b_i = b_f * SCALE_FL;
  a_q = a_i *1.0/ SCALE_FL;    // quant value
  b_q = b_i *1.0/ SCALE_FL;

  c_i = a_i + b_i;
  c_q = c_i*1.0 / SCALE_FL;
  c_f = a_f + b_f;


  printf("# ADD Test\n");
  printf("# Data Quant Fraction length is %d bit\n", FL);
  printf("# a_f =  %-10f, a_i = %-8d 0x%-8x , a_q = %f\n", a_f, a_i, a_i, a_q);
  printf("# b_f =  %-10f, b_i = %-8d 0x%-8x , b_q = %f\n", b_f, b_i, b_i, b_q);
  printf("# c_f =  %-10f, c_i = %-8d 0x%-8x , c_q = %f\n", c_f, c_i, c_i, c_q);
  printf("#\n");

}

float_check(){


  float v_f = 1.125;
  void   *p = NULL;
  unsigned int v_f_i = 0;
  unsigned int S, E, M;
  
  printf("# Float Check\n");
  p = &v_f;
  v_f_i = *((unsigned int *) p);
  printf("# v_f = %f, hex val v_f_i = 0x%x \n", v_f, v_f_i );
  S = v_f_i >> 31; E = (v_f_i >> 23)&((1 << 8) - 1); M = v_f_i & (( 1 << 23)-1);
  printf("# S = %d, E = %d, M = 0x%x \n", S, E, M);
  printf("#\n");


}
main(){

  printf("# Fixed point Demo LAB\n\n");
  mult_test();
  add_test();
  float_check();
 

  printf("# \n");
  printf("# Done, press Enter key to quit\n");
  getch();
}