深入剖析回归（二）L1，L2正则项，梯度下降

一、回归问题的定义

回归是监督学习的一个重要问题，回归用于预测输入变量和输出变量之间的关系。回归模型是表示输入变量到输出变量之间映射的函数。回归问题的学习等价于函数拟合：使用一条函数曲线使其很好的拟合已知函数且很好的预测未知数据。

回归问题分为模型的学习和预测两个过程。基于给定的训练数据集构建一个模型，根据新的输入数据预测相应的输出。

回归问题按照输入变量的个数可以分为一元回归和多元回归；按照输入变量和输出变量之间关系的类型，可以分为线性回归和非线性回归。

 

一元回归：y = ax + b

多元回归：

二、回归问题的求解

2.1解析解

2.1.1 最小二乘法

最小二乘法又称最小平方法，它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。

2.1.2利用极大似然估计解释最小二乘法

现在假设我们有m个样本，我们假设有：

误差项是IID，根据中心极限定理，由于误差项是好多好多相互独立的因素影响的综合影响，我们有理由假设其服从高斯分布，又由于可以自己适配theta0，是的误差项的高斯分布均值为0，所以我们有

所以我们有：

也即：

 表示在theta给定的时候，给我一个x，就给你一个y

那么我们可以写出似然函数：

由极大似然估计的定义，我们需要L(theta)最大，那么我们怎么才能是的这个值最大呢？两边取对数对这个表达式进行化简如下：

需要 l(theta)最大，也即最后一项的后半部分最小，也即：

目标函数（损失函数）

所以，我们最后由极大似然估计推导得出，我们希望 J(theta) 最小，而这刚好就是最小二乘法做的工作。而回过头来我们发现，之所以最小二乘法有道理，是因为我们之前假设误差项服从高斯分布，假如我们假设它服从别的分布，那么最后的目标函数的形式也会相应变化。

好了，上边我们得到了有极大似然估计或者最小二乘法，我们的模型求解需要最小化目标函数J(theta)，那么我们的theta到底怎么求解呢？有没有一个解析式可以表示theta?

2.1.3 theta的解析式的求解过程

我们需要最小化目标函数，关心 theta 取什么值的时候，目标函数取得最小值，而目标函数连续，那么 theta 一定为 目标函数的驻点，所以我们求导寻找驻点。

求导可得：

最终我们得到参数 theta 的解析式：

 关于向量、矩阵求导知识参见 http://www.cnblogs.com/futurehau/p/6105236.html

上述最后一步有一些问题，假如 X'X不可逆呢？

我们知道 X'X 是一个半正定矩阵，所以若X'X不可逆或为了防止过拟合，我们增加lambda扰动，得到

从另一个角度来看，这相当与给我们的线性回归参数增加一个惩罚因子，这是必要的，我们数据是有干扰的，不正则的话有可能数据对于训练集拟合的特别好，但是对于新数据的预测误差很大。

2.1.4正则化

L2-norm: （Ridge回归）

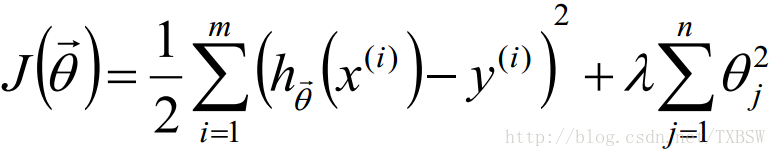
L1-norm: （Lasso回归）

　　

L1-norm 和 L2-norm都能防止过拟合，一般L2-norm的性能更好一些。L1-norm能够进行特选择对数据进行降维 产生稀疏模型，能够帮助我们去除某些特征，因此可以用于特征选择。

Elastic Net：

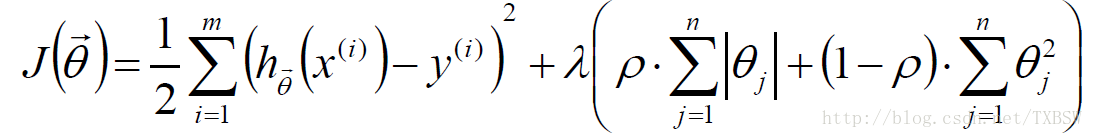
L1-norm 和 L2-norm都能防止过拟合，一般L2-norm的效果更好一些。L1-norm能够产生稀疏模型，能够帮助我们去除某些特征，因此可以用于特征选择。

L1-norm 和 L2-norm的直观理解：摘自 http://lib.csdn.net/article/machinelearning/42049

 

正则化（Regularization）

机器学习中几乎都可以看到损失函数后面会添加一个额外项，常用的额外项一般有两种，一般英文称作 ℓ 1 -norm 和 ℓ 2 -norm ，中文称作 L1正则化 和 L2正则化 ，或者 L1范数 和 L2范数 。

L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓『惩罚』是指对损失函数中的某些参数做一些限制。对于线性回归模型，使用L1正则化的模型建叫做Lasso回归，使用L2正则化的模型叫做Ridge回归（岭回归）。下图是Python中Lasso回归的损失函数，式中加号后面一项 α | | w | | 1 即为L1正则化项。

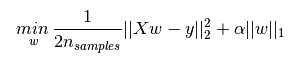
下图是Python中Ridge回归的损失函数，式中加号后面一项 α | | w | | 2 2 即为L2正则化项。

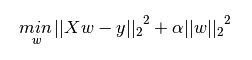
一般回归分析中回归 w 表示特征的系数，从上式可以看到正则化项是对系数做了处理（限制）。 L1正则化和L2正则化的说明如下：

• L1正则化是指权值向量w中各个元素的绝对值之和，通常表示为||w||1
• L2正则化是指权值向量w中各个元素的平方和然后再求平方根（可以看到Ridge回归的L2正则化项有平方符号），通常表示为||w||2

一般都会在正则化项之前添加一个系数，Python中用 α 表示，一些文章也用 λ 表示。这个系数需要用户指定。

那添加L1和L2正则化有什么用？ 下面是L1正则化和L2正则化的作用 ，这些表述可以在很多文章中找到。

• L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择
• L2正则化可以防止模型过拟合（overfitting）；一定程度上，L1也可以防止过拟合

稀疏模型与特征选择

上面提到L1正则化有助于生成一个稀疏权值矩阵，进而可以用于特征选择。为什么要生成一个稀疏矩阵？

稀疏矩阵指的是很多元素为0，只有少数元素是非零值的矩阵，即得到的线性回归模型的大部分系数都是0. 通常机器学习中特征数量很多，例如文本处理时，如果将一个词组（term）作为一个特征，那么特征数量会达到上万个（bigram）。在预测或分类时，那么多特征显然难以选择，但是如果代入这些特征得到的模型是一个稀疏模型，表示只有少数特征对这个模型有贡献，绝大部分特征是没有贡献的，或者贡献微小（因为它们前面的系数是0或者是很小的值，即使去掉对模型也没有什么影响），此时我们就可以只关注系数是非零值的特征。这就是稀疏模型与特征选择的关系。

L1和L2正则化的直观理解

这部分内容将解释 为什么L1正则化可以产生稀疏模型（L1是怎么让系数等于零的） ，以及 为什么L2正则化可以防止过拟合 。

L1正则化和特征选择

假设有如下带L1正则化的损失函数： 

J = J 0 + α ∑ w | w | (1)

其中 J 0 是原始的损失函数，加号后面的一项是L1正则化项， α 是正则化系数。注意到L1正则化是权值的 绝对值之和 ， J 是带有绝对值符号的函数，因此 J 是不完全可微的。机器学习的任务就是要通过一些方法（比如梯度下降）求出损失函数的最小值。当我们在原始损失函数 J 0 后添加L1正则化项时，相当于对 J 0 做了一个约束。令 L = α ∑ w | w | ，则 J = J 0 + L ，此时我们的任务变成 在 L 约束下求出 J 0 取最小值的解 。考虑二维的情况，即只有两个权值 w 1 和 w 2 ，此时 L = | w 1 | + | w 2 | 对于梯度下降法，求解 J 0 的过程可以画出等值线，同时L1正则化的函数 L 也可以在 w 1 w 2 的二维平面上画出来。如下图：

 

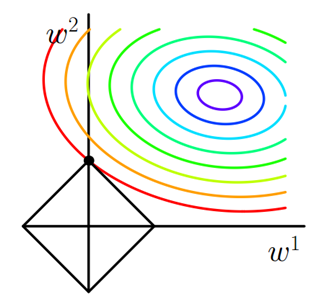
图1 L1正则化

图中等值线是 J 0 的等值线，黑色方形是 L 函数的图形。在图中，当 J 0 等值线与 L 图形首次相交的地方就是最优解。上图中 J 0 与 L 在 L 的一个顶点处相交，这个顶点就是最优解。注意到这个顶点的值是 ( w 1 , w 2 ) = ( 0 , w ) 。可以直观想象，因为 L 函数有很多『突出的角』（二维情况下四个，多维情况下更多）， J 0 与这些角接触的机率会远大于与 L 其它部位接触的机率，而在这些角上，会有很多权值等于0，这就是为什么L1正则化可以产生稀疏模型，进而可以用于特征选择。

而正则化前面的系数 α ，可以控制 L 图形的大小。 α 越小， L 的图形越大（上图中的黑色方框）； α 越大， L 的图形就越小，可以小到黑色方框只超出原点范围一点点，这是最优点的值 ( w 1 , w 2 ) = ( 0 , w ) 中的 w 可以取到很小的值。

类似，假设有如下带L2正则化的损失函数： 

J = J 0 + α ∑ w w 2 (2)

同样可以画出他们在二维平面上的图形，如下：

 

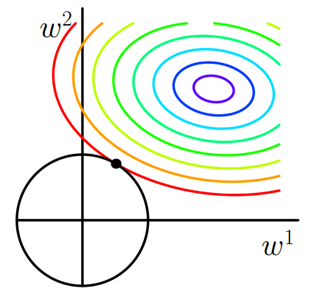
图2 L2正则化

二维平面下L2正则化的函数图形是个圆，与方形相比，被磨去了棱角。因此 J 0 与 L 相交时使得 w 1 或 w 2 等于零的机率小了许多，这就是为什么L2正则化不具有稀疏性的原因。

L2正则化和过拟合

拟合过程中通常都倾向于让权值尽可能小，最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程，若参数很大，那么只要数据偏移一点点，就会对结果造成很大的影响；但如果参数足够小，数据偏移得多一点也不会对结果造成什么影响，专业一点的说法是『抗扰动能力强』。

那为什么L2正则化可以获得值很小的参数？

以线性回归中的梯度下降法为例。假设要求的参数为 θ， h θ ( x )是我们的假设函数，那么线性回归的代价函数如下： 

J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) (3)

那么在梯度下降法中，最终用于迭代计算参数 θ 的迭代式为：  

θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x ( i ) j (4)

其中 α 是learning rate. 上式是没有添加L2正则化项的迭代公式，如果在原始代价函数之后添加L2正则化，则迭代公式会变成下面的样子：  

θ j : = θ j ( 1 − α λ m ) − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x ( i ) j (5)

其中 λ 就是正则化参数 。从上式可以看到，与未添加L2正则化的迭代公式相比，每一次迭代， θ j 都要先乘以一个小于1的因子，从而使得 θ j 不断减小，因此总得来看， θ 是不断减小的。

最开始也提到L1正则化一定程度上也可以防止过拟合。之前做了解释，当L1的正则化系数很小时，得到的最优解会很小，可以达到和L2正则化类似的效果。

正则化参数的选择

L1正则化参数

通常越大的 λ 可以让代价函数在参数为0时取到最小值。下面是一个简单的例子，这个例子来自 Quora上的问答 。为了方便叙述，一些符号跟这篇帖子的符号保持一致。

假设有如下带L1正则化项的代价函数： 

F ( x ) = f ( x ) + λ | | x | | 1

其中 x 是要估计的参数，相当于上文中提到的 w 以及 θ . 注意到L1正则化在某些位置是不可导的，当 λ 足够大时可以使得 F ( x ) 在 x = 0 时取到最小值。如下图：

 

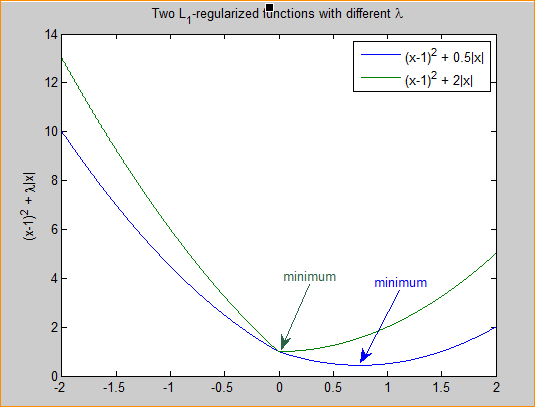
图3 L1正则化参数的选择

分别取 λ = 0.5 和 λ = 2 ，可以看到越大的 λ 越容易使 F ( x ) 在 x = 0 时取到最小值。

L2正则化参数

从公式5可以看到， λ 越大， θ j 衰减得越快。另一个理解可以参考图2， λ 越大，L2圆的半径越小，最后求得代价函数最值时各参数也会变得很小。

 2.2 梯度下降算法

我们在上边给出了最小二乘法求解线性回归的参数theta,实际python 的 numpy库就是使用的这种方法。

当然了，这需要我们的参数的维度不大，当维度大的时候，使用解析解就不适用了，这里讨论梯度下降算法。

2.2.1梯度下降法步骤：

　　初始化theta

　　沿着负梯度方向迭代，更新后的theta使得J(theta)更小。

　　其中α：学习率 步长

　　

梯度下系那个示意图如下：

每次迭代找到一个更好的，最后得到一个局部最优解，不一定是全局最优，但是是堪用的。

2.2.2 具体实现

梯度方向：

2.2.2.1 批量梯度下降算法：(BGD)

由于在线性回归中，目标函数收敛而且为凸函数，是有一个极值点，所以局部最小值就是全局最小值。

2.2.2.2随机梯度下降算法：(SGD)

拿到一个样本就下降一次。实际中随机梯度下降算法其实是更适用的。出于一下亮点考虑：

1.由于噪声的存在，不能保证每个变量都让目标函数下降，但总的趋势是下降的。但是另一方面，由于噪声的存在，随机梯度下降算法往往有利于跳出局部最小值。

2.流式数据的处理

2.2.2.3 mini-batch SGD(实际中都是简称为SGD)

拿到若干个样本的平均梯度之后在更新梯度方向。

SGD随机梯度下降

如上图所示，一个批量梯度下降，一个随机梯度下降，最终效果其实是相近的。

今天先搞这么多吧，虽然是东拼西凑的，但是这些都是我自己理解过之后才去粘贴的

上个经典的干货：

#!/usr/bin/python
# -*- coding:utf-8 -*-

import numpy as np
from sklearn.linear_model import LinearRegression, RidgeCV, LassoCV, ElasticNetCV
from sklearn.preprocessing import PolynomialFeatures
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.exceptions import ConvergenceWarning
import matplotlib as mpl
import warnings

def xss(y, y_hat):
    y = y.ravel()
    y_hat = y_hat.ravel()
    # Version 1
    tss = ((y - np.average(y)) ** 2).sum()
    rss = ((y_hat - y) ** 2).sum()
    ess = ((y_hat - np.average(y)) ** 2).sum()
    r2 = 1 - rss / tss
    # print 'RSS:', rss, '\t ESS:', ess
    # print 'TSS:', tss, 'RSS + ESS = ', rss + ess
    tss_list.append(tss)
    rss_list.append(rss)
    ess_list.append(ess)
    ess_rss_list.append(rss + ess)
    # Version 2
    # tss = np.var(y)
    # rss = np.average((y_hat - y) ** 2)
    # r2 = 1 - rss / tss
    corr_coef = np.corrcoef(y, y_hat)[0, 1]
    return r2, corr_coef


if __name__ == "__main__":
    warnings.filterwarnings(action='ignore', category=ConvergenceWarning)
    np.random.seed(0)
    np.set_printoptions(linewidth=1000)
    N = 9
    x = np.linspace(0, 6, N) + np.random.randn(N)
    x = np.sort(x)
    y = x**2 - 4*x - 3 + np.random.randn(N)
    x.shape = -1, 1
    y.shape = -1, 1
    print("- - - - -")
    # 形如 1.00000000e+02  表示1.000*10^2 即1.00乘以10的2次幂
    print (np.logspace(-3, 2, 5))
    print(np.logspace(-2, 9, 5))
    print(np.logspace(0, 0, 5))
    print(np.logspace(0, 1, 5))
    print('- - - - - -')
    # 线性回归的目的是要得到输出向量Y和输入特征X之间的线性关系,求出线性回归系数θ，也就是Y=Xθ,
    # 其中Y的维度为mx1,X的维度为mxn，而θ的维度为nx1,m代表样本个数,n代表样本特征的维度

    # 损失函数:损失函数是用来评价模型的预测值f(x)与真实值Y的不一致程度,它是一个非负实值函数 通常用L(Y,f(x))表示,损失函数越小,模型的性能就越好
    # 正则化项:为了防止损失函数过拟合的问题，一般会在损失函数中加上正则化项,增加模型的泛化能力
    models = [Pipeline([
        ('poly', PolynomialFeatures()),
        # 损失函数:J(θ)=1/2(Xθ−Y)T(Xθ−Y) 优化方法：梯度下降和最小二乘法,scikit中采用最小二乘
        # 使用场景:只要数据线性相关，LinearRegression是我们的首选,如果发现拟合或者预测的不够好，再考虑其他的线性回归库
        ('linear', LinearRegression(fit_intercept=False))]),
        # Ridge回归(岭回归)损失函数的表达形式：J(θ)=1/2(Xθ−Y)T(Xθ−Y)+1/2α||θ||22(线性回归LineaRegression的损失函数+L2（2范式的正则化项）)
        # a为超参数 alphas=np.logspace(-3, 2, 50) 从给定的超参数a中选择一个最优的,logspace用于创建等比数列 本例中 开始点为10的-3次幂,结束点10的2次幂,元素个数为
        # 50,并且从这50个数中选择一个最优的超参数
        # linspace创建等差数列
        # Ridge回归中超参数a和回归系数θ的关系,a越大，正则项惩罚的就越厉害，得到的回归系数θ就越小,最终趋近与0
        # 如果a越小,即正则化项越小，那么回归系数θ就越来越接近于普通的线性回归系数

        # 使用场景:只要数据线性相关，用LinearRegression拟合的不是很好，需要正则化，可以考虑使用RidgeCV回归,
        # 如何输入特征的维度很高,而且是稀疏线性关系的话， RidgeCV就不太合适,考虑使用Lasso回归类家族
        Pipeline([
            ('poly', PolynomialFeatures()),
            ('linear', RidgeCV(alphas=np.logspace(-3, 2, 50), fit_intercept=False))]),
        Pipeline([
            ('poly', PolynomialFeatures()),
            # 损失函数:J(θ)=1/2m(Xθ−Y)T(Xθ−Y)+α||θ||1 线性回归LineaRegression的损失函数+L1（1范式的正则化项）)
            # Lasso回归可以使得一些特征的系数变小,甚至还使一些绝对值较小的系数直接变为0，从而增强模型的泛化能力
            # 使用场景:对于高纬的特征数据,尤其是线性关系是稀疏的，就采用Lasso回归,或者是要在一堆特征里面找出主要的特征，那么
            # Lasso回归更是首选了
            ('linear', LassoCV(alphas=np.logspace(-3, 2, 50), fit_intercept=False))]),
        Pipeline([
            ('poly', PolynomialFeatures()),
            # 损失函数：J(θ)=1/2m(Xθ−Y)T(Xθ−Y)+αρ||θ||1+α(1−ρ)/2||θ||22  其中α为正则化超参数，ρ为范数权重超参数
            # alphas=np.logspace(-3, 2, 50), l1_ratio=[.1, .5, .7, .9, .95, .99, 1] ElasticNetCV会从中选出最优的 a和p
            # ElasticNetCV类对超参数a和p使用交叉验证，帮助我们选择合适的a和p
            # 使用场景:ElasticNetCV类在我们发现用Lasso回归太过(太多特征被稀疏为0),而Ridge回归也正则化的不够(回归系数衰减太慢)的时候
            ('linear', ElasticNetCV(alphas=np.logspace(-3, 2, 50), l1_ratio=[.1, .5, .7, .9, .95, .99, 1],
                                    fit_intercept=False))])
    ]
    mpl.rcParams['font.sans-serif'] = [u'simHei']
    mpl.rcParams['axes.unicode_minus'] = False
    np.set_printoptions(suppress=True)

    plt.figure(figsize=(18, 12), facecolor='w')
    d_pool = np.arange(1, N, 1)  # 阶
    m = d_pool.size
    print("==================",m)
    clrs = []  # 颜色
    print(np.linspace(16711680, 255, m))
    for c in np.linspace(16711680, 255, m):
        clrs.append("#%06x" % int(c))

    line_width = np.linspace(5, 2, m)
    titles = '线性回归', u'Ridge回归', u'LASSO', u'ElasticNet'
    tss_list = []
    rss_list = []
    ess_list = []
    ess_rss_list = []
    for t in range(4):
        model = models[t]
        plt.subplot(2, 2, t+1)
        plt.plot(x, y, 'ro', ms=10, zorder=N)
        for i, d in enumerate(d_pool):
            model.set_params(poly__degree=d)
            model.fit(x, y.ravel())
            lin = model.get_params('linear')['linear']
            output = '%s：%d阶，系数为：' % (titles[t], d)
            if hasattr(lin, 'alpha_'):
                idx = output.find('系数')
                output = output[:idx] + ('alpha=%.6f，' % lin.alpha_) + output[idx:]
            if hasattr(lin, 'l1_ratio_'):   # 根据交叉验证结果，从输入l1_ratio(list)中选择的最优l1_ratio_(float)
                idx = output.find(u'系数')
                output = output[:idx] + (u'l1_ratio=%.6f，' % lin.l1_ratio_) + output[idx:]
            print (output, lin.coef_.ravel())
            x_hat = np.linspace(x.min(), x.max(), num=100)
            x_hat.shape = -1, 1
            y_hat = model.predict(x_hat)
            s = model.score(x, y)
            r2, corr_coef = xss(y, model.predict(x))
            # print 'R2和相关系数：', r2, corr_coef
            # print 'R2：', s, '\n'
            z = N - 1 if (d == 2) else 0
            label = '%d阶，$R^2$=%.3f' % (d, s)
            if hasattr(lin, 'l1_ratio_'):
                label += '，L1 ratio=%.2f' % lin.l1_ratio_
            plt.plot(x_hat, y_hat, color=clrs[i], lw=line_width[i], alpha=0.75, label=label, zorder=z)
        plt.legend(loc='upper left')
        plt.grid(True)
        plt.title(titles[t], fontsize=18)
        plt.xlabel('X', fontsize=16)
        plt.ylabel('Y', fontsize=16)
    plt.tight_layout(1, rect=(0, 0, 1, 0.95))
    plt.suptitle(u'多项式曲线拟合比较', fontsize=22)
    plt.show()

    y_max = max(max(tss_list), max(ess_rss_list)) * 1.05
    plt.figure(figsize=(9, 7), facecolor='w')
    t = np.arange(len(tss_list))
    plt.plot(t, tss_list, 'ro-', lw=2, label=u'TSS(Total Sum of Squares)')
    plt.plot(t, ess_list, 'mo-', lw=1, label=u'ESS(Explained Sum of Squares)')
    plt.plot(t, rss_list, 'bo-', lw=1, label=u'RSS(Residual Sum of Squares)')
    plt.plot(t, ess_rss_list, 'go-', lw=2, label=u'ESS+RSS')
    plt.ylim((0, y_max))
    plt.legend(loc='center right')
    plt.xlabel(u'实验：线性回归/Ridge/LASSO/Elastic Net', fontsize=15)
    plt.ylabel(u'XSS值', fontsize=15)
    plt.title(u'总平方和TSS=？', fontsize=18)
    plt.grid(True)
    plt.show()

加点小东西: