作者水平有限,欢迎大家提出文中错误
矩阵方程、线性方程组
A x = b Ax=b Ax=b的行图像
行图像就是在高中一直学习的函数图像,交点为方程组的解
A
=
[
r
o
w
1
(
A
)
r
o
w
2
(
A
)
⋮
r
o
w
m
(
A
)
]
A= \left[ \begin{matrix} row\ 1(A)\\ row\ 2(A)\\ \vdots\\ row\ m(A) \end{matrix} \right]
A=⎣⎢⎢⎢⎡row 1(A)row 2(A)⋮row m(A)⎦⎥⎥⎥⎤
A
x
=
[
r
o
w
1
(
A
)
⋅
x
r
o
w
2
(
A
)
⋅
x
⋮
r
o
w
m
(
A
)
⋅
x
]
=
[
b
1
b
2
⋮
b
m
]
Ax= \left[ \begin{matrix} row\ 1(A)·x\\ row\ 2(A)·x\\ \vdots\\ row\ m(A)·x \end{matrix} \right] = \left[ \begin{matrix} b_1\\ b_2\\ \vdots\\ b_m \end{matrix} \right]
Ax=⎣⎢⎢⎢⎡row 1(A)⋅xrow 2(A)⋅x⋮row m(A)⋅x⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡b1b2⋮bm⎦⎥⎥⎥⎤
[
3
1
1
−
1
]
[
x
1
x
2
]
=
[
1
0
]
\left[ \begin{matrix} 3 & 1\\ 1 & -1\\ \end{matrix} \right] \left[ \begin{matrix} {x_1}\\ {x_2} \end{matrix} \right]= \left[ \begin{matrix} 1\\ 0 \end{matrix} \right]
[311−1][x1x2]=[10]

A x = b Ax=b Ax=b的列图像
列图像强调
A
x
Ax
Ax其实是矩阵
A
A
A各列的线性组合
A
=
[
c
o
l
u
m
n
1
(
A
)
c
o
l
u
m
n
3
(
A
)
…
c
o
l
u
m
n
n
(
A
)
]
A= \left[ \begin{matrix} column\ 1(A) &column\ 3(A) \dots &column\ n(A) \end{matrix} \right]
A=[column 1(A)column 3(A)…column n(A)]
A
x
=
∑
i
=
1
n
x
i
c
o
l
u
m
n
i
(
A
)
=
b
Ax=\sum\limits^n_{i=1}x_i\ column\ i(A) =b
Ax=i=1∑nxi column i(A)=b
[
3
1
1
−
1
]
[
x
1
x
2
]
=
[
1
0
]
\left[ \begin{matrix} 3 & 1\\ 1 & -1\\ \end{matrix} \right] \left[ \begin{matrix} {x_1}\\ {x_2} \end{matrix} \right]= \left[ \begin{matrix} 1\\ 0 \end{matrix} \right]
[311−1][x1x2]=[10]

齐次方程 A x = 0 Ax=0 Ax=0
直接举例:
A
=
[
1
2
2
2
2
4
6
8
3
6
8
10
]
A= \left[ \begin{matrix} 1&2&2&2\\ 2&4&6&8\\ 3&6&8&10 \end{matrix} \right]
A=⎣⎡1232462682810⎦⎤
E
21
,
e
21
=
−
2
E_{21},e_{21}=-2
E21,e21=−2
E
31
,
e
31
=
−
3
E_{31},e_{31}=-3
E31,e31=−3
[
1
2
2
2
0
0
2
4
0
0
2
4
]
\left[ \begin{matrix} 1&2&2&2\\ 0&0&2&4\\ 0&0&2&4 \end{matrix} \right]
⎣⎡100200222244⎦⎤
E
32
,
e
32
=
−
1
E_{32},e_{32}=-1
E32,e32=−1
U
=
[
1
2
2
2
0
0
2
4
0
0
0
0
]
(
e
c
h
e
l
o
n
f
o
r
m
)
U= \left[ \begin{matrix} 1&2&2&2\\ 0&0&2&4\\ 0&0&0&0 \end{matrix} \right](echelon\ form)
U=⎣⎡100200220240⎦⎤(echelon form)
注意此处
U
U
U矩阵有两个主元,所以
r
a
n
k
A
=
2
rank\ A=2
rank A=2
主元所在列被称为主列
p
i
v
o
t
c
o
l
u
m
n
pivot\ column
pivot column,其他列被称为自由列
f
r
e
e
c
o
l
u
m
n
free\ column
free column
对于线性方程组,主元位置对应的变量被称为主变量
p
i
v
o
t
v
a
r
i
a
b
l
e
s
pivot\ variables
pivot variables,其他变量为自由变量
f
r
e
e
v
a
r
i
a
b
l
e
s
free\ variables
free variables
算法继续,将方程组的矩阵形式写回方程组
{
x
1
+
2
x
2
+
2
x
3
+
2
x
4
=
0
2
x
3
+
4
x
4
=
0
\left\{ \begin{aligned} x_1+2x_2+2x_3+2x_4=0\\ 2x_3+4x_4=0 \end{aligned} \right.
{x1+2x2+2x3+2x4=02x3+4x4=0
为什么说
x
2
,
x
4
x_2,x_4
x2,x4是自由变量,是因为
x
2
,
x
4
x_2,x_4
x2,x4可自由取值,通过回代,确定
x
1
,
x
3
x_1,x_3
x1,x3
令
x
2
=
1
,
x
4
=
0
x_2=1,x_4=0
x2=1,x4=0,则
x
1
=
−
2
,
x
3
=
0
x_1=-2,x_3=0
x1=−2,x3=0
令
x
2
=
0
,
x
4
=
1
x_2=0,x_4=1
x2=0,x4=1,则
x
1
=
2
,
x
3
=
−
2
x_1=2,x_3=-2
x1=2,x3=−2
至此求出了
N
(
A
)
N(A)
N(A)的两个基,而这两个基可以张成整个零空间,因为
d
i
m
N
(
A
)
=
n
−
r
=
2
dim\ N(A)=n-r=2
dim N(A)=n−r=2,对这两个基线性组合,每一种线性组合都是
A
x
=
0
Ax=0
Ax=0的解。
但是其实矩阵
U
U
U还可以进一步化简为简化行阶梯形式
R
(
R
e
d
u
c
e
d
r
o
w
e
c
h
e
l
o
n
f
o
r
m
)
R(Reduced\ row\ echelon\ form)
R(Reduced row echelon form)
算法继续
U
=
[
1
2
2
2
0
0
2
4
0
0
0
0
]
U= \left[ \begin{matrix} 1&2&2&2\\ 0&0&2&4\\ 0&0&0&0 \end{matrix} \right]
U=⎣⎡100200220240⎦⎤
E
12
,
e
12
=
−
1
E_{12},e_{12}=-1
E12,e12=−1
U
=
[
1
2
0
−
2
0
0
2
4
0
0
0
0
]
U= \left[ \begin{matrix} 1&2&0&-2\\ 0&0&2&4\\ 0&0&0&0 \end{matrix} \right]
U=⎣⎡100200020−240⎦⎤
最后对
r
o
w
2
row\ 2
row 2做数乘
R
=
[
1
2
0
−
2
0
0
1
2
0
0
0
0
]
(
R
e
d
u
c
e
d
r
o
w
e
c
h
e
l
o
n
f
o
r
m
)
R= \left[ \begin{matrix} 1&2&0&-2\\ 0&0&1&2\\ 0&0&0&0 \end{matrix} \right](Reduced\ row\ echelon\ form)
R=⎣⎡100200010−220⎦⎤(Reduced row echelon form)
其实从
U
U
U到
R
R
R的向上的消元,相当于回代
可以发现
R
R
R的主元列主元行中包含了一个单位阵
I
I
I
R
P
23
=
[
1
0
2
−
2
0
1
0
2
0
0
0
0
]
RP_{23}= \left[ \begin{matrix} 1&0&2&-2\\ 0&1&0&2\\ 0&0&0&0 \end{matrix} \right]
RP23=⎣⎡100010200−220⎦⎤
其中左乘置换矩阵代表列交换
可以将矩阵分块
R
P
23
=
[
I
F
O
O
]
RP_{23}= \left[ \begin{matrix} I&F\\ O&O\\ \end{matrix} \right]
RP23=[IOFO]
整个方程化为
R
P
23
P
32
x
=
0
RP_{23}P_{32}x=0
RP23P32x=0,其中
P
32
x
=
[
x
1
x
3
x
2
x
4
]
=
[
x
p
i
v
o
t
x
f
r
e
e
]
P_{32}x= \left[ \begin{matrix} x_1\\ x_3\\ x_2\\ x_4\\ \end{matrix} \right]= \left[ \begin{matrix} x_{pivot}\\ x_{free}\\ \end{matrix} \right]
P32x=⎣⎢⎢⎡x1x3x2x4⎦⎥⎥⎤=[xpivotxfree]
[
I
F
O
1
∗
2
O
1
∗
2
]
[
x
p
i
v
o
t
x
f
r
e
e
]
=
[
O
2
∗
1
O
2
∗
1
]
\left[ \begin{matrix} I&F\\ O_{1*2}&O_{1*2}\\ \end{matrix} \right] \left[ \begin{matrix} x_{pivot}\\ x_{free}\\ \end{matrix} \right]= \left[ \begin{matrix} O_{2*1}\\ O_{2*1}\\ \end{matrix} \right]
[IO1∗2FO1∗2][xpivotxfree]=[O2∗1O2∗1]
下面构建一个零空间矩阵
N
(
N
u
l
l
s
p
a
c
e
m
a
t
r
i
c
e
s
)
N(Null \ space\ matrices)
N(Null space matrices),满足
R
N
=
0
RN=0
RN=0
零空间矩阵的各列可张成整个零空间
沿用方程
R
P
23
P
32
x
=
0
RP_{23}P_{32}x=0
RP23P32x=0
P
32
N
=
[
X
p
i
v
o
t
X
f
r
e
e
]
P_{32}N= \left[ \begin{matrix} X_{pivot}\\ X_{free}\\ \end{matrix} \right]
P32N=[XpivotXfree]
则
[
I
F
O
1
∗
2
O
1
∗
2
]
[
X
p
i
v
o
t
X
f
r
e
e
]
=
[
O
2
∗
1
O
2
∗
1
]
\left[ \begin{matrix} I&F\\ O_{1*2}&O_{1*2}\\ \end{matrix} \right] \left[ \begin{matrix} X_{pivot}\\ X_{free}\\ \end{matrix} \right]= \left[ \begin{matrix} O_{2*1}\\ O_{2*1}\\ \end{matrix} \right]
[IO1∗2FO1∗2][XpivotXfree]=[O2∗1O2∗1]
I
X
p
i
v
o
t
+
F
X
f
r
e
e
=
O
2
∗
1
IX_{pivot}+FX_{free}=O_{2*1}
IXpivot+FXfree=O2∗1
解得
[
I
F
O
1
∗
2
O
1
∗
2
]
[
−
F
I
]
=
[
O
2
∗
1
O
2
∗
1
]
\left[ \begin{matrix} I&F\\ O_{1*2}&O_{1*2}\\ \end{matrix} \right] \left[ \begin{matrix} -F\\ I\\ \end{matrix} \right]= \left[ \begin{matrix} O_{2*1}\\ O_{2*1}\\ \end{matrix} \right]
[IO1∗2FO1∗2][−FI]=[O2∗1O2∗1]
X
p
i
v
o
t
=
−
F
=
[
−
2
2
0
−
2
]
X_{pivot}=-F= \left[ \begin{matrix} -2&2\\ 0&-2\\ \end{matrix} \right]
Xpivot=−F=[−202−2]
X
f
r
e
e
=
I
=
[
1
1
]
X_{free}=I= \left[ \begin{matrix} 1&\\ &1\\ \end{matrix} \right]
Xfree=I=[11]
消掉置换阵
N
=
[
−
2
2
1
0
0
−
2
0
1
]
N= \left[ \begin{matrix} -2&2\\ 1&0\\ 0&-2\\ 0&1\\ \end{matrix} \right]
N=⎣⎢⎢⎡−210020−21⎦⎥⎥⎤
可以证明
C
(
N
)
=
N
(
A
)
C(N)=N(A)
C(N)=N(A)
非齐次方程 A x = b Ax=b Ax=b
例子1:
[
1
2
2
2
2
4
6
8
3
6
8
10
]
[
x
1
x
2
x
3
x
4
]
=
[
b
1
b
2
b
3
]
\left[ \begin{matrix} 1&2&2&2\\ 2&4 &6&8 \\ 3&6&8&10\\ \end{matrix} \right] \left[ \begin{matrix} x_1\\ x_2\\ x_3\\ x_4\\ \end{matrix} \right] =\left[ \begin{matrix} b_1\\ b_2\\ b_3\\ \end{matrix} \right]
⎣⎡1232462682810⎦⎤⎣⎢⎢⎡x1x2x3x4⎦⎥⎥⎤=⎣⎡b1b2b3⎦⎤
构造增广矩阵
A
u
g
u
m
e
n
t
M
a
t
r
i
c
e
s
[
A
∣
b
]
Augument\ Matrices[A|b]
Augument Matrices[A∣b]
[
1
2
2
2
2
4
6
8
3
6
8
10
b
1
b
2
b
3
]
\left [ \begin{array}{c:c} \begin{matrix} 1&2&2&2\\ 2&4 &6&8 \\ 3&6&8&10\\ \end{matrix}& \begin{matrix} b_1\\ b_2\\ b_3\\ \end{matrix} \end{array} \right ]
⎣⎡1232462682810b1b2b3⎦⎤
通过高斯消元得到
[
1
2
2
2
0
0
2
4
0
0
0
0
b
1
b
2
−
2
b
1
b
3
−
b
2
−
b
1
]
\left [ \begin{array}{c:c} \begin{matrix} 1&2&2&2\\ 0&0 &2&4 \\ 0&0&0&0\\ \end{matrix}& \begin{matrix} b_1\\ b_2-2b_1\\ b_3-b_2-b_1\\ \end{matrix} \end{array} \right ]
⎣⎡100200220240b1b2−2b1b3−b2−b1⎦⎤
可见如果
b
3
−
b
2
−
b
1
≠
0
b_3-b_2-b_1\not=0
b3−b2−b1=0方程无解,原因是那样的话
b
∉
C
(
A
)
b\notin C(A)
b∈/C(A)
假设
b
=
(
1
,
5
,
6
)
b=(1,5,6)
b=(1,5,6)
[
1
2
2
2
0
0
2
4
0
0
0
0
1
3
0
]
\left [ \begin{array}{c:c} \begin{matrix} 1&2&2&2\\ 0&0 &2&4 \\ 0&0&0&0\\ \end{matrix}& \begin{matrix} 1\\ 3\\ 0\\ \end{matrix} \end{array} \right ]
⎣⎡100200220240130⎦⎤
写成线性方程组
{
x
1
+
2
x
2
+
2
x
3
+
2
x
4
=
1
2
x
3
+
4
x
4
=
3
\left\{ \begin{aligned} x_1+2x_2+2x_3+2x_4=1\\ 2x_3+4x_4=3 \end{aligned} \right.
{x1+2x2+2x3+2x4=12x3+4x4=3
首先找一个特解,不妨设所有自由变量都等于0,得
{
x
1
+
0
+
2
x
3
+
0
=
1
2
x
3
+
0
=
3
\left\{ \begin{aligned} x_1+\ \ 0\ \ +2x_3+\ \ 0\ \ =1\\ 2x_3+\ \ 0\ \ =3 \end{aligned} \right.
{x1+ 0 +2x3+ 0 =12x3+ 0 =3
解得
x
3
=
1.5
,
x
1
=
−
2
x_3=1.5,x_1=-2
x3=1.5,x1=−2,则有特解
x
p
a
r
t
i
c
u
l
a
r
=
(
−
2
,
0
,
1.5
,
0
)
x_{particular}=(-2,\ 0,\ 1.5,\ 0)
xparticular=(−2, 0, 1.5, 0)
为什么要先找一个特解,因为对于非齐次线性方程组,解的结构是
x
=
x
p
a
r
t
i
c
u
l
a
r
+
x
n
u
l
l
s
p
a
c
e
x=x_{particular}+x_{null\ space}
x=xparticular+xnull space
证明:
已知
A
x
p
a
r
t
i
c
u
l
a
r
=
b
Ax_{particular}=b
Axparticular=b
A
x
n
u
l
l
s
p
a
c
e
=
0
Ax_{null\ space}=0
Axnull space=0
两边分别相加
A
(
x
p
a
r
t
i
c
u
l
a
r
+
x
n
u
l
l
s
p
a
c
e
)
=
b
A(x_{particular}+x_{null\ space})=b
A(xparticular+xnull space)=b
证毕
所以接下来,只需要求解 N ( A ) N(A) N(A),即可完成求解
A x = b Ax=b Ax=b的解空间
上一节,得知解的结构是
x
=
x
p
a
r
t
i
c
u
l
a
r
+
x
n
u
l
l
s
p
a
c
e
x=x_{particular}+x_{null\ space}
x=xparticular+xnull space
可以看出解空间
S
=
x
p
a
r
t
i
c
u
l
a
r
+
N
(
A
)
S=x_{particular}+N(A)
S=xparticular+N(A),显然
S
S
S不再是向量空间,而是由向量空间
N
(
A
)
N(A)
N(A)平移了(或加上)
x
p
a
r
t
i
c
u
l
a
r
x_{particular}
xparticular的不过原点的空间。
比如线性方程
1
2
x
+
y
−
2
z
=
a
\frac{1}{2}x+y-2z=a
21x+y−2z=a,解空间随
a
a
a的变化如下

r a n k A rank\ A rank A与可解性
行列都不满秩
对于
r
<
m
,
r
<
n
r<m,r<n
r<m,r<n的矩阵方程
A
x
=
b
Ax=b
Ax=b,由矩阵列图像可知只有当
b
∈
C
(
A
)
b \in C(A)
b∈C(A),方程才有解
A
=
[
3
1
−
1
−
3
−
1
1
]
,
b
=
[
a
1
]
A=\left[ \begin{matrix} 3 & 1 & -1\\ -3 & -1 & 1\\ \end{matrix} \right], b=\left[ \begin{matrix} a\\ 1\\ \end{matrix} \right]
A=[3−31−1−11],b=[a1]
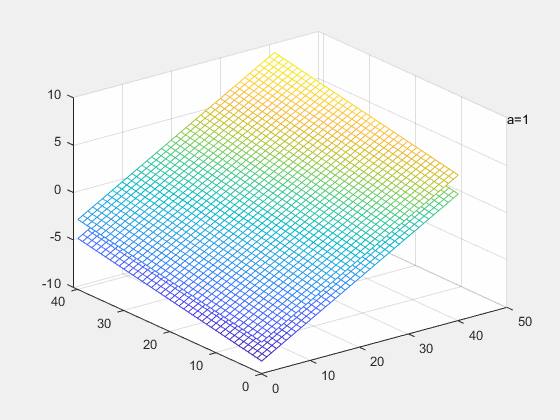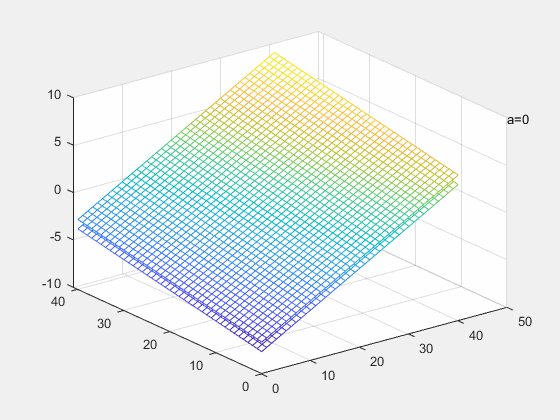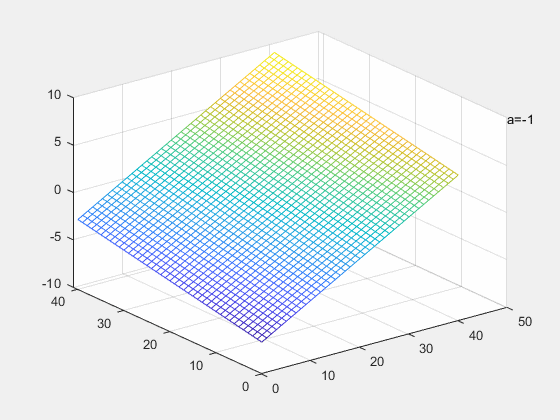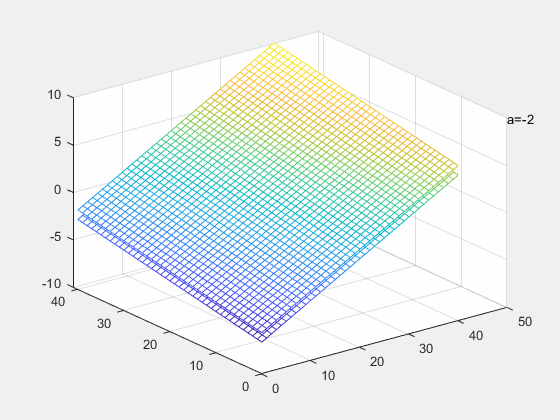
a
=
−
1
a=-1
a=−1,两平面重合,此时方程有无穷解
a
=
1
a=1
a=1,两平面平行,此时方程有无解
此类矩阵的
R
R
E
F
(
R
e
d
u
c
e
d
r
o
w
e
c
h
e
l
o
n
f
o
r
m
)
RREF(Reduced\ row\ echelon\ form)
RREF(Reduced row echelon form)形状为
R
=
[
I
F
O
O
]
R= \left[ \begin{matrix} I & F\\ O & O\\ \end{matrix} \right]
R=[IOFO]
行满秩,列未满秩
此时称线性方程组是欠定的
A
=
[
3
1
1
−
3
1
−
1
]
,
b
=
[
a
1
]
A=\left[ \begin{matrix} 3 & 1 & 1\\ -3 & 1 & -1\\ \end{matrix} \right], b=\left[ \begin{matrix} a\\ 1\\ \end{matrix} \right]
A=[3−3111−1],b=[a1]
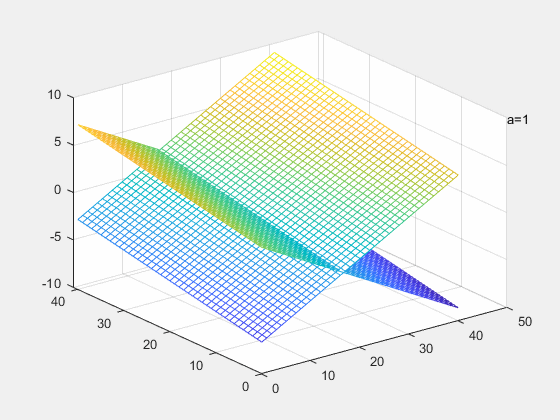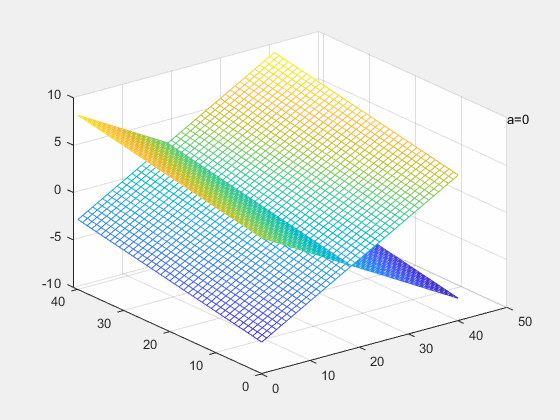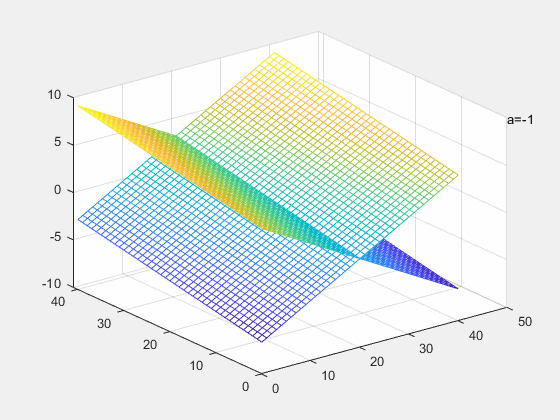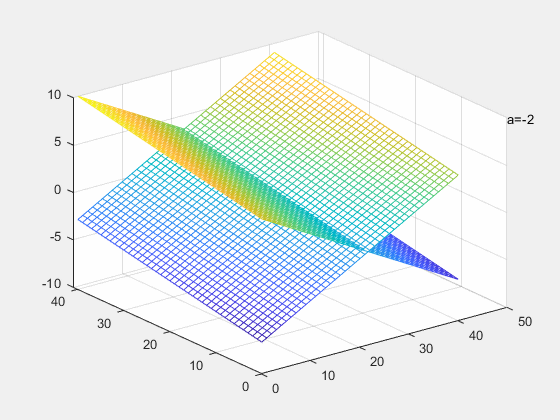
当行满秩的时候,解空间的维度是
n
−
m
n-m
n−m。因为
d
i
m
C
(
A
)
=
m
dim\ C(A)=m
dim C(A)=m,所以
∀
b
∈
R
m
,
b
∈
C
(
A
)
\forall\ b\in\mathbb R^m,b\in C(A)
∀ b∈Rm,b∈C(A),对任意
b
b
b总有解而解无穷
此类矩阵的
R
R
E
F
RREF
RREF形状为
R
=
[
I
F
]
R= \left[ \begin{matrix} I & F\\ \end{matrix} \right]
R=[IF]
列满秩,行未满秩
此时称线性方程组是超定的
A
=
[
3
−
3
1
1
2
−
1
]
,
b
=
[
a
0
1
]
A=\left[ \begin{matrix} 3&-3\\ 1&1\\ 2&-1\\ \end{matrix} \right], b=\left[ \begin{matrix} a\\ 0\\ 1\\ \end{matrix} \right]
A=⎣⎡312−31−1⎦⎤,b=⎣⎡a01⎦⎤
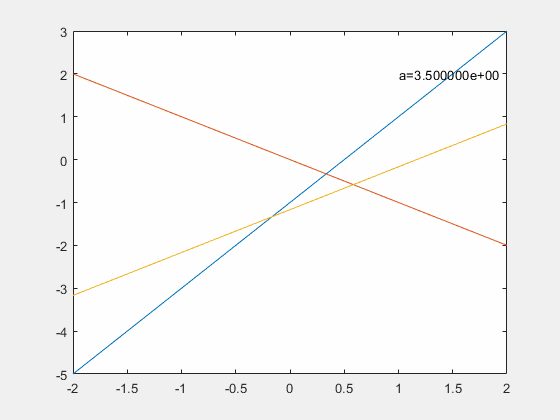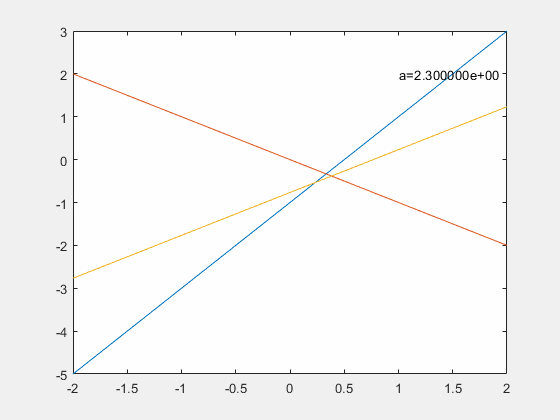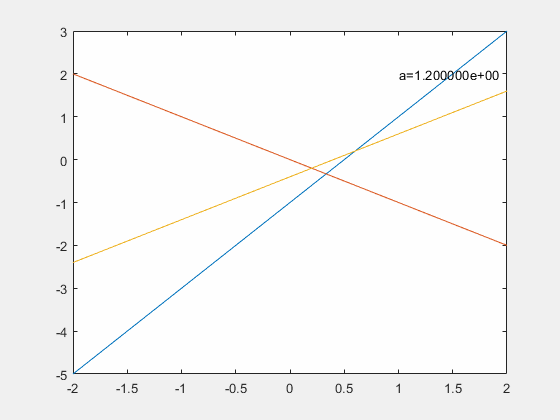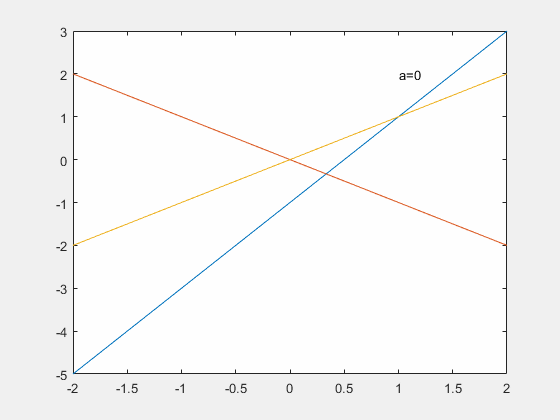
在列满秩的时候,只有当
b
∈
C
(
A
)
b\in C(A)
b∈C(A)时,
A
x
=
b
Ax=b
Ax=b有唯一解,否则无解
此类矩阵的
R
R
E
F
RREF
RREF形状为
R
=
[
I
O
]
R= \left[ \begin{matrix} I\\ O\\ \end{matrix} \right]
R=[IO]
N
(
A
)
=
{
0
}
N(A)=\{0\}
N(A)={0}
满秩
A
=
[
1
0
1
1
1
2
0
−
1
1
]
,
b
=
[
1
1
1
]
A=\left[ \begin{matrix} 1&0&1\\ 1&1 &2 \\ 0&-1&1\\ \end{matrix} \right], b=\left[ \begin{matrix} 1\\ 1\\ 1\\ \end{matrix} \right]
A=⎣⎡11001−1121⎦⎤,b=⎣⎡111⎦⎤

满秩情况下,
A
x
=
b
Ax=b
Ax=b总有解且唯一
此类矩阵的
R
R
E
F
RREF
RREF形状为
R
=
I
R=I
R=I
总之, A x = b Ax=b Ax=b要想可解,充分必要条件是 b ∈ C ( A ) b\in C(A) b∈C(A);而解要想唯一, A A A各列必须线性无关。






















 3753
3753











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








