古诺模型里的纳什均衡

最新推荐文章于 2024-12-18 21:42:14 发布

密言

最新推荐文章于 2024-12-18 21:42:14 发布

阅读量7.3k

点赞数 8

文章标签：学习

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/ThePythonFucker/article/details/124150553

版权

古诺模型描述了两个寡头企业在同质化商品市场中的竞争。每个企业的利润最大化策略是根据对方的产量决定自身产量。市场价格由总产量决定，且随着产量增加而下降。纳什均衡是双方都无法单方面改变策略以提高利润的状态，即两个企业的产量在成本线与需求曲线交点处。然而，这种均衡可能不稳定，因为企业可能会试图偏离均衡以获取更多利润，导致新竞争者的进入。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

古诺模型：市场一共两个参与者

他们的策略就是商品的产量（假设商品都是同质化，也就是一模一样的），设为 $q_{i}$ ，如 $q_{1}$ , $q_{2}$

生产1单位的成本为c

生产成本就是

$c*q_{i}$

如何制定市场价格呢

价格由如下因素决定：两个参数 $a$ 和 $b$

核心思想是两家企业生产越多，商品的市场价格就越低

画图（下图被称为需求曲线）：

横坐标 $q_{1}+q_{2}$ 表示总产量，纵坐标 $P$ 表示市场价格，截距为 $a$ ，斜率为 $-b$

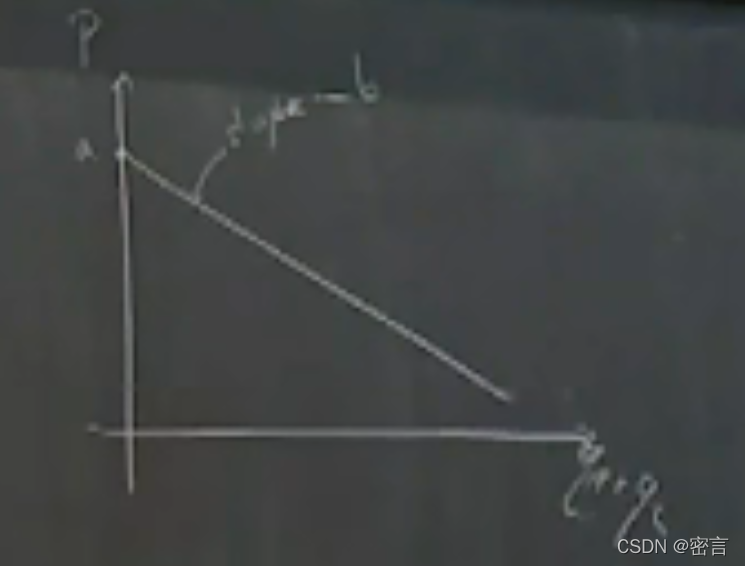
$P$ 是给定的价格，曲线就是对应的需求量

对于公司1来说，它的利润（收益-成本）为

$U(q_{1},q_{2})=P*q_{1}-c*q_{1}$

将需求曲线的公式

$P=a-b(q_{1}+q_{2})$

代入，替换P

就可以得到公司1的利润表达式，同理也可以求出公司2的表达式

$U=a*q_{1}-b*q_{1}^{2}-b*q_{1}*q_{2}-c*q_{1}$

下面如何求出纳什均衡？

我们可以求出参与人1对于2不同产量下的最佳产量，以及参与人2对于1不同产量下的最佳产量（说人话就是对2的每一种选择都找到1在此条件下的最优选择，然后所有的选择连成一条线就是一的曲线）

思路很简单，我们只需要对 $U$ 中的 $q_{1}$ 求导，求二阶导是为了验证确实存在最大值

BR(q2)的图像为

当 $q_{1}$ 取0时， $q_{2}$ 的产量就是

$(a-c)/b$

放到下图里就是成本线和原先曲线的交点，当处于此状态时， $q_{1}$ 如果继续生产，会使点沿曲线右移，会使市场价格低于成本，导致亏本

同理，我们可以用红色的笔画出在 $q_{1}$ 的不同选择下 $q_{2}$ 的最佳应对策略，两条线的交点就是他们的纳什均衡，也就是古诺产出

这不是策略互补博弈，而是策略替代博弈，换句话说，一方增加，另一方就要减少

$A B C$ 三点都达到了市场利润最高，但是双方无法达成协议去保持 $B$ 点的产量，因为总会有一方偷偷改变产量使之达到纳什均衡，最终仍然会回到交点

即使不考虑偷偷违约，在 $B$ 点会吸引新加入者，最终导致新的竞争

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。