【文献阅读】A Survey of Low-bit Large Language Models: Basics, Systems, and Algorithms

arXiv:2409.16694v2 [cs.AI] 30 Sep 2024 9月30

低比特大语言模型综述：基础、系统与算法

摘要

大语言模型（LLMs）在自然语言处理领域取得了显著进展，在各种任务中展现出卓越的性能。然而，高昂的内存和计算需求给其实际部署带来了巨大挑战。低比特量化作为一种关键方法，通过减少模型参数、激活值和梯度的比特宽度，降低了内存使用和计算需求。本文全面综述了针对大语言模型的低比特量化方法，涵盖了基本原理、系统实现和算法策略。首先介绍了低比特大语言模型的基本概念和特定的数据格式，接着回顾了支持不同硬件平台上低比特大语言模型的框架和系统。然后，我们对大语言模型高效低比特训练和推理的技术和工具包进行了分类和分析。最后，我们讨论了低比特大语言模型的未来趋势和潜在进展。从基础、系统和算法的角度进行的系统综述，能够为未来通过低比特量化提高大语言模型的效率和适用性提供有价值的见解和指导。

关键词：大语言模型；量化；低比特；系统；算法

 1 引言

大语言模型（LLMs）（OpenAI等人，2024；图夫龙等人，2023a，2023b；杜比等人，2024；洛日科夫等人，2024；刘等人，2024a）在从文本生成到语言理解等一系列任务中实现了前所未有的性能，彻底改变了自然语言处理领域。然而，它们强大的能力伴随着巨大的计算和内存需求。这在资源有限或高并发的场景中部署这些模型时带来了相当大的挑战。为了解决这些挑战，低比特量化已成为提高大语言模型效率和可部署性的关键方法。

低比特量化是指减少张量比特宽度的过程，这有效地降低了大语言模型的内存占用和计算需求。通过用低比特整数/二进制表示压缩大语言模型的权重、激活值和梯度，量化可以在可接受的精度范围内显著加速推理和训练，并减少存储需求。这种效率对于使先进的大语言模型能够在资源受限的设备上使用至关重要，从而拓宽了它们的应用范围。

图1：LLM量化方法的框架。该图说明了调查的主要领域。 

本文旨在全面综述大语言模型的低比特量化，涵盖与低比特大语言模型相关的基本概念、系统实现和算法方法。与传统模型相比，大语言模型作为基础模型的代表范式，通常具有大量参数，这给有效的量化带来了独特的挑战。如图1所示，第2节介绍了大语言模型低比特量化的基础知识，包括特定于大语言模型的新低比特数据格式和量化粒度。第3节回顾了支持不同硬件平台上低比特大语言模型的系统和框架。然后，我们在第4节和第5节分别对高效训练和推理的低比特量化技术进行分类。对于训练，我们讨论了大语言模型低比特训练和微调的方法。对于推理，我们根据量化感知训练和训练后量化对大语言模型量化方法进行区分。量化感知训练通常用于低比特设置（如二进制量化）。训练后量化在现有研究中更常用，因为它是一种资源高效的流程。为了便于理解，我们首先介绍广泛使用的用于减少异常值影响的等效变换和用于减轻量化误差的权重补偿技术。然后讨论混合精度、将量化与其他压缩方法相结合的技术，以及新量化形式的方法。此外，我们总结了集成这些算法以支持准确低比特大语言模型开发的工具包。最后，第6节探索未来的趋势和方向，讨论新兴的研究领域、潜在的突破以及新技术对大语言模型量化的影响。我们的综述详细描述了低比特大语言模型的基础，全面介绍了通过低比特量化加速训练和推理的系统实现，以及保持和提高量化精度的算法和策略。我们相信这项综述能够提供有价值的见解，并推动大语言模型量化的发展。

 2 低比特大语言模型基础

在本节中，我们从三个方面介绍量化和低比特大语言模型的基本原理：（1）低比特数字格式。为了处理大语言模型中的异常值，低比特浮点数首先被用于量化。并且设计了许多自定义数据格式来处理异常值。然而，整数仍然是主流。（2）量化粒度。为了提高量化大语言模型的性能，更细粒度的量化可以保留更多信息并产生更好的结果。但粗粒度的量化占用更少的存储空间，推理效率更高。（3）动态或静态量化。动态量化不需要校准，因为量化参数是实时计算的，这使得量化模型的准备更加简单。相比之下，静态量化需要对量化参数进行预校准，但它提供更快的推理性能。

 2.1 低比特数字格式

在介绍开始时，我们先从低比特数字格式入手。首先，我们展示被广泛认可的标准格式，但重点关注大语言模型中的差异。其次，我们介绍一些为大语言模型设计的典型自定义格式。

 2.1.1 标准格式

 浮点数：浮点数数据类型在IEEE 754（IEEE，2019）标准中被全面定义，这也是计算机系统中最常用的数字格式。我们将其表示为\(FPk\)，其中\(k\)表示该值在内存中占用的比特数，通常为32、16、8等。浮点数可以统一表示为： \(X_{FP k}=(-1)^{s} 2^{p-bias}(1.mantissa )=(-1)^{s} 2^{p-bias}\left(1+\frac{d_{1}}{2}+\frac{d_{2}}{2^{2}}+...+\frac{d_{m}}{2^{m}}\right)\) 其中，\(s\)是符号位，\(p\)是指数整数，\(bias\)是应用于指数的偏移量，\(m\)是尾数部分的总比特数，\(d_{1}, d_{2}, ..., d_{m}\)表示二进制格式的尾数部分的数字。

对于\(FPk\)值，\(s\)、\(p\)和\(m\)的比特数之和应为\(k\)。 由于大语言模型占用更多内存，较低比特的格式在训练和推理中都被广泛采用。这里我们省略32位数字格式，因为16位及更低比特宽度已成为应用中的主流实践。我们可以根据指数（\(E\)）和尾数（\(M\)）部分的比特分配进一步对每个\(FPk\)进行分类。我们用\(EeMm\)表示子类别。对于\(FP16\)，IEEE 754定义了\(float16\)（也称为半精度或\(FP16\)）和\(bfloat16\)（脑浮点或\(BF16\)），它们可以分别表示为\(E5M10\)和\(E8M7\)。因此，\(bfloat16\)可以用更多的指数比特（与\(FP32\)相同）表示更大的数值范围，同时由于尾数部分比特较少，比\(float16\)更稀疏，这在大语言模型中可能具有前所未有的潜力（亨利等人，2019）。对于\(FP8\)，还有\(E4M3\)和\(E5M2\)，它们都是标准格式，已被一些主流深度学习推理引擎支持，如\(MLC-LLM\)、\(Quanto\)等（详见第3.1.2节）。 

\(NormalFloat\)（\(NF\)）（德特默斯等人，2024）是一种用于大语言模型仅权重量化策略的固定浮点数方法。其数据表示格式遵循浮点数，但\(X_{i}^{NF}\)（\(i \in [0,2^{k}-1]\)）的\(2^{k}\)个值估计为： \(X_{i}^{NF}=\frac{1}{2}\left( quantile \left(N(0,1), \frac{i}{2^{k}+1}\right)+ quantile \left(N(0,1), \frac{i+1}{2^{k}+1}\right)\right)\) 其中，\(quantile (\cdot, q)\)是输入的第\(q\)个分位数，\(N(0,1)\)表示标准正态分布。对于不在 -1到1范围内的张量，我们必须首先使用其最大绝对值对其进行缩放。

为了确保对零的精确表示，它通过估计\(X_{i}^{NF}\)的\(2^{k - 1}\)个值用于负数部分，\(2^{k - 1}-1\)个值用于正数部分，不对称地将数据分为正负两部分，然后在两组中各去除一个零值。\(NF\)估计在每个量化区间内具有几乎相等数量的值，以在量化格式中保留最多信息。 \(Micro Scaling FP\)（鲁哈尼等人，2023）由包括AMD、Arm、英特尔、Meta、微软、英伟达和高通在内的行业联盟成员共同提出和开发，旨在为张量格式的细粒度子块建立统一标准。它对具有各种原始格式（即\(FP8\)、\(FP6\)、\(FP4\)、\(INT8\)）的数据块应用\(E8M0\)缩放因子。缩放块大小表示每个缩放应用的元素数量。它在保持高精度值表示的同时，由于共享缩放，在硬件上具有显著的高效性。 整数：自量化技术出现以来，整数量化就是研究最广泛的量化数据格式。它将浮点数划分为\(2^{k}\)个等间距的离散整数。

公式为： \(X_{INT_{k}}=(-1)^{s}\left(d_{1} 2^{m}+d_{2} 2^{m - 1}+\cdots+d_{m} 2^{0}\right), x \in \mathbb{N}^{+}\) 其中，对于有符号整数，\(m = k - 1\)且\(s \in \{0,1\}\)；对于无符号整数，\(m = k\)且我们认为\(s = 0\)。因此，有符号整数的范围是\([-2^{k - 1}, 2^{k - 1}-1]\)，无符号整数的范围是\([0, 2^{k}-1]\)。 二值化数：二值化是最激进的量化技术，它直接提取值的符号（刘等人，2018；秦等人，2022；李等人，2024d）。这会丢失大部分信息，但在推理中能带来显著的加速和参数压缩。硬件最初将每个比特视为0或1，但开发人员定义不同的逻辑规则和累加算法来实现各种二值化计算。

因此，浮点数可以二值化为\(\{-1, 1\}\)或\(\{0, 1\}\)，这取决于我们在算法中期望单个比特代表什么值。 表1展示了各种标准格式的表示范围。可以看出，即使比特宽度相同，不同的数值表示格式也可能具有显著不同的值范围。具有较大\(E\)的浮点数表示范围更大，但点更稀疏。因此，在为特定模型和任务确定数据格式时，需要在更细的数据区间和更大的数据范围之间进行权衡。

表1 不同数字格式的最小值和最大值（IEEE，2019）

 2.1.2 自定义格式

为了实现更快的计算并更好地拟合大语言模型的数值分布，除了上述标准格式外，许多研究还提出了自定义数字格式。这里我们介绍三种典型的自定义格式。我们省略大语言模型出现之前的工作（坦贝等人，2019），因为它们在大语言模型上的性能尚未得到验证。
 浮点整数（Flint）（郭等人，2022）结合了浮点和整数表示的优点，其表达式为\(X_{Flint }=2^{p - bias } \times(1.mantissa)\)。以基于浮点的乘加单元上的4位Flint为例：
\(p=\left\{\begin{array}{ll} 3-LZD\left( b_{2} b_{1} b_{0}\right), & b_{3}=0 \\ 4+LZD\left(b_{2} b_{1} b_{0}\right), & b_{3}=1 \end{array},\right. mantissa =b_{2} b_{1} b_{0} \ll\left( LZD\left( b_{2} b_{1} b_{0}\right)+1\right)\)
其中，\(LZD\)表示前导零检测器（奥克洛布季亚，1994），用于累积比特串左侧的前导零，\(\ll\)是左移操作，对于基于浮点的Flint4，\(bias = 1\)。它通过将指数集成到整数中来扩展范围。与纯整数相比，Flint可以用有限的比特数表示更大的范围，更适合大语言模型参数的分布。
 自适应偏置浮点（Abfloat）：在异常值 - 受害者对量化（\(OVP\)）（郭等人，2023a）中首次提出，用于处理异常值。与Flint的区别在于，Abfloat对指数应用更大的偏置，并左移\(m\)位以放大尾数前的1，使数值范围更大以覆盖异常值。\(EeMm\)格式的Abfloat值可以表示为：
\(X_{Abffloat }=(-1)^{s} × 2^{p+ bias } \times\left(2^{m}+ mantissa \right)\)
当\(bias = 0\)时，范围与Flint4相似。当\(E2M1\)格式且\(bias = 2\)时，范围变为\(\{12,..,9\}\)。当\(bias = 3\)时，范围进一步扩展到\((24,..,192)\)。与Flint的另一个区别是，Abfloat仅用于异常值，而正常的值存储为\(INT4/8\)或Flint4。这两种数据格式都需要自定义系统支持来定义基本操作（如加法、乘法等）的行为。
 学生浮点（SF）（多策尔等人，2024a）遵循浮点格式，但具有特定的量化固定点，这与上述两种类型不同。\(SF\)是对2.1.1节中\(NF\)的改进，认为参数服从学生t分布\(S(t ; \nu)\)，其概率密度函数为：
\(S(t ; \nu)=\frac{\Gamma\left(\frac{\nu+1}{2}\right)}{\sqrt{\nu \pi} \Gamma\left(\frac{\nu}{2}\right)}\left(1+\frac{t^{2}}{\nu}\right)^{-\frac{\nu+1}{2}}\)
其中，\(t\)和\(\nu\)分别是自变量和自由度，\(\Gamma\)是广义阶乘。
\(\tilde{X}_{i}^{SF}= quantile \left(S(t ; \nu), q_{i}\right), q_{i}=\left\{\begin{array}{ll} \omega+\left(\frac{1}{2}-\omega\right) \frac{i-1}{7} & i \in\{1, ..., 8\} \\ \frac{1}{2}+\left(\frac{1}{2}-\omega\right) \frac{i-8}{8} & i \in\{9, ..., 16\} \end{array}\right.\)
其中\(\omega=\frac{1}{2}(\frac{1}{32}+\frac{1}{30})\)，\(\{q_{1}, ..., q_{8}\}\)和\(\{q_{9}, ..., 16\}\)是两组均匀间隔的分位数。然后我们通过\(X_{i}^{SF}=\frac{\tilde{X}_{i}^{SF}}{max _{i}|\tilde{X}_{i}^{SF}|}\)将\(\tilde{X}^{SF}\)归一化到\([-1,1]\)。随着\(\nu\)增加，t分布的峰值变得更短更宽，\(SF4\)分布更分散。当\(\nu \to \infty\)时，它收敛到标准正态分布（\(NF\)）。与\(NF\)一样，\(SF\)用于仅权重量化（我们将在3.2.1节介绍）。因此，它不需要对基本操作进行底层定义，但需要从\(SF\)到标准格式的自定义反量化。

图2：不同量化粒度的图示。

 2.2 量化粒度

量化粒度是指与缩放因子和零点的每个元素相对应的不同权重/激活分区。它决定了缩放恢复的精细程度和零点的偏移量。图2展示了五种基本的量化粒度类型：张量级、词元级、通道级、组级和元素级。

张量级是最简单、最粗糙的粒度，它对整个张量使用单个缩放因子和零点（张等人，2024c）。它可能是最快的，但可能导致最大的性能下降，因为它无法处理变化范围较大的值。因此，它不适用于精度重要或任务/模型对量化敏感的情况。

词元级仅在大语言模型中使用，意味着每个词元（单词或子单词）都有一个缩放（姚等人，2022

词元级仅在大语言模型中使用，意味着每个词元（单词或子单词）都有一个缩放（姚等人，2022）。它捕捉了不同词元中的细粒度变化。通常，我们对激活采用动态词元级量化，以减少量化误差并确保生成模型中的多样性。

通道级意味着张量内权重的每个通道使用一个缩放，并且可以合并到量化权重中（金等人，2024）。词元级激活和通道级权重通常一起使用。因为对于激活中的第\(i\)个词元和权重中的第\(j\)个通道，相应的\(s_{x_{i}} \in s_{x} \in \mathbb{R}^{T ×1}\)和\(s_{w_{j}} \in s_{w} \in \mathbb{R}^{1 ×C}\)可以首先计算为\(s \in \mathbb{R}^{[1]}\)，并与输出矩阵\(x_{O}\)中的坐标\([i, j]\)相乘。通过这种方式，我们在几乎不增加计算开销的情况下保留了生成性能。

组级通过将具有相同缩放因子的张量或通道分组，平衡了计算复杂度和量化误差。如果每组有\(g\)个词元/通道，它还可以将缩放因子的存储减少\(g\)倍（河野等人，2023；姚等人，2022）。

元素级仅在训练权重时应用，并且总是与另一种量化粒度（如张量级）一起使用（见图2（e））。在推理之前，元素级缩放会合并到量化权重中。因此，在推理时只需要计算张量级缩放来恢复值的大小（李等人，2023）。

不同的量化粒度通常会结合使用。例如，李等人（2023）根据数据分布，对键矩阵使用通道级缩放，对值矩阵使用词元级缩放。更多算法可在5.2.3节中找到。

 2.3 动态和静态量化

动态和静态量化主要指训练后量化（PTQ）中的策略，如图3所示。我们以整数量化为例，其他低比特量化方法的过程类似。

动态量化（克里希纳莫尔蒂，2018；刘等人，2022）校准并存储量化后的权重。通常，它不需要输入数据，而是通过最小化每个权重张量的量化误差来搜索最优的缩放因子\(s_{w}\)和零点\(Z_{w}\)。在推理时，激活值将输入到量化模块中，计算最优的缩放因子\(s_{x}\)和\(Z_{x}\)，然后在与量化权重进行整数通用矩阵乘法（GEMM）之前，通过动态计算的因子将其量化为INT8。激活值的缩放和零点是根据当前输入数据批次实时获得的。因此，缩放因子可以灵活地适应输入数据的分布，带来最小的量化误差。不过，在推理时获取缩放因子会增加额外的计算复杂度。它适用于需要快速部署的场景，因为它不需要校准。

图3 动态和静态量化。绿色框中的操作表示推理过程，框外是生产和准备过程

这张图展示了动态量化（Dynamic Quant）和静态量化（Static Quant）的两种不同方式（权重和激活量化、仅权重量化 ），具体如下：

动态量化（Dynamic Quant）
准备阶段（Preparing）：对权重 \( W_{FP} \) 进行量化，获取量化参数 \( s_w \)（缩放因子）和 \( z_w \)（零点 ），得到量化后的权重 \( W_{INT} \) 。此过程可以使用校准数据（calibration data），也可以不使用数据（data free） 。
推理阶段（Inference）：输入的激活值 \( X_{FP} \) 在推理时才进行量化，获取其量化参数 \( s_x \) 和 \( z_x \) ，得到量化后的激活值 \( X_{INT} \) ，然后使用整数矩阵乘法内核（INT MatMul Kernels）进行计算。动态量化的特点是在推理时实时计算激活值的量化参数，无需提前对激活值进行校准 。

静态量化 - 权重和激活量化（Static Quant - weight & activation）
准备阶段（Preparing）：分别对权重 \( W_{FP} \) 和激活值 \( X_{FP} \)（来自下一层）进行量化，获取权重的量化参数 \( s_w \)、\( z_w \) 和激活值的量化参数 \( s_x \)、\( z_x \) ，得到量化后的权重 \( W_{INT} \) 和激活值 \( X_{INT} \) 。此过程需要校准数据 。
推理阶段（Inference）：量化后的权重 \( W_{INT} \) 和激活值 \( X_{INT} \) 直接使用整数矩阵乘法内核（INT MatMul Kernels）进行计算。由于提前对激活值也进行了校准量化，推理时计算效率更高 。
 
静态量化 - 仅权重量化（Static Quant - weight only）
准备阶段（Preparing）：对权重 \( W_{FP} \) 进行量化，获取量化参数 \( s_w \)、\( z_w \) ，得到量化后的权重 \( W_{INT} \) 。可以使用校准数据或不使用数据 。
推理阶段（Inference）：量化后的权重 \( W_{INT} \) 先进行反量化（Dequantize）变回 \( W_{FP} \) ，然后与输入的激活值 \( X_{FP} \) 一起使用浮点矩阵乘法内核（FP MatMul Kernels）进行计算。这种方式只对权重进行量化，在一些场景下可减少权重存储和传输成本 。

校准数据是什么？：在量化过程中，校准数据（calibration data）是用于确定量化参数（如缩放因子、零点等 ）的数据集合。具体来说：作用原理：通过将校准数据输入模型，观察模型中张量（如权重、激活值）的分布情况。基于这些数据的统计特征，比如均值、标准差、最大值、最小值等，来计算合适的量化参数，使得量化后的模型能在尽量减少精度损失的前提下运行 。例如在确定缩放因子时，可能需要根据校准数据中张量元素的取值范围，找到一个合适的缩放比例，让量化后的数值能较好地近似原始浮点数值。使用场景：主要用于静态量化场景。因为静态量化需要提前确定量化参数，校准数据提供了一个样本集，帮助准确地计算这些参数。而动态量化由于是在推理时实时计算量化参数，虽然也可以使用校准数据来辅助初始化某些参数，但对校准数据的依赖程度相对较低 。数据要求：校准数据应尽可能与模型实际运行时处理的数据分布相似。例如对于一个用于图像分类的神经网络，校准数据应选取具有代表性的图像样本，涵盖不同类别、不同光照、不同分辨率等各种实际场景中可能出现的情况，这样确定的量化参数才能让模型在实际推理时表现良好 。

校准数据怎么获得呢？：在量化模型领域获取校准数据，常见方法如下： 从原始数据集选取
随机抽样：从模型训练使用的原始数据集中，按照一定比例随机抽取数据作为校准数据。例如在图像分类任务中，从海量图像数据里随机选出若干张图像及其对应的标签，组成校准数据集。这样能保证校准数据与原始数据分布相似，让b量化参数适应模型正常处理的数据特征。分层抽样：当原始数据集存在类别不平衡等情况时，采用分层抽样。比如在文本情感分类任务里，数据集包含积极、消极、中性文本数量差异较大，按不同情感类别分层，从每一层按相应比例抽取文本，确保校准数据涵盖各类别特征，使量化参数能兼顾不同类别的数据特性 。 人工合成数据——基于规则生成：针对特定任务，依据一定规则生成数据。在语音识别领域，可利用语音合成工具，按照常见语音模式、语速、语调等规则生成模拟语音数据，作为校准数据，补充真实语音数据不足，丰富数据多样性。生成对抗网络（GAN）等技术：借助 GAN 或变分自编码器（VAE）等深度学习模型生成数据。如在医学图像量化校准中，使用 GAN 让生成器学习真实医学图像分布，生成类似但不同的图像作为校准数据，扩充数据量，还能生成一些少见的病理图像情况，提升模型对复杂情况的适应性 。 领域内公开数据集——许多领域有公开的标准数据集，可直接选用或部分选用作为校准数据。如计算机视觉领域的 ImageNet 、MNIST 数据集；自然语言处理领域的 GLUE 、SQuAD 数据集等。这些数据集经过广泛研究和验证，数据质量高、分布明确，使用它们能让校准过程更具通用性和可比性，也便于与其他研究成果进行对比分析 。

静态量化（白等人，2021）使用一小部分训练数据集作为校准数据。通过将样本输入模型，我们找到权重和激活（图3中间）或仅权重（图3右侧）的最优缩放因子，并在推理过程中固定这些因子。这允许在准备阶段评估量化模型，确保量化不会显著损害模型性能。对于推理，图3中间将激活量化为低比特，并与量化权重进行低比特通用矩阵乘法（德特默斯等人，2022b）。对于图3右侧，权重将被反量化为浮点数，在进行浮点通用矩阵乘法（林等人，2024a）之前，激活不会被量化，因此我们将其称为仅权重量化。

 3 框架和系统支持

在大语言模型出现后的短短几年里，出现了许多支持大语言模型便捷使用的框架。在本节中，我们选择了一些与量化相关的知名代表性框架和工具，并根据以下类别进行总结和介绍：（1）量化推理框架，为大语言模型应用的快速开发和部署提供全面的库和应用程序编程接口（API）；（2）量化系统支持，为量化方法提供底层核心功能。接下来，我们重点关注不同框架和库中对大语言模型的量化支持。

 3.1 量化推理框架

我们在表2中列出了代表性的推理框架。目前，在性能或使用方面没有单一的推理框架占据主导地位。然而，一些经典的深度学习框架，如TensorRT - LLM、ONNX - runtime、Transformers（Huggingface）、OpenVINO、PowerInfer、PPLNN和Xorbits Inference，已经集成了对大模型高效推理的支持。此外，在大模型出现后出现的其他推理框架，是专门为大语言模型提出的，如bitsandbytes、ctransformers、MLC - LLM、DeepSpeed - MII、vLLM、LMDeploy、LightLLM、QServe、llama.cpp、llama2.c、inferflow、ScaleLLM、SGLang、gpt - fast、FastChat、OpenLLM等。这些框架轻量级，并集成了许多针对大模型的专门优化技术。

Framework	Algorithms	Model family	Device or Engine	W bit &A bit	Weight - only bit	KV Cache bit	Granularity	Institution
TensorRT - LLM	AWQ, GPTQ, SmoothQuant	Mixture - of - Expert (e.g. Mixtral), Transformer - like (e.g. Llama), Multi - modal LLMs (e.g. LLaVA)	NVIDIA GPU	W fp8 A fp8, W int8 A int8, W int4 A fp8	int4, int8	fp16, fp8, int8	tensor - wise, token - wise, channel - wise, group - wise(128)	NVIDIA
Transformers	AQLM, AWQ, AutoGPTQ, EETQ, HQQ, ExLlama, QAT, Quanto, SmoothQuant	Mixture - of - Expert (e.g. Mixtral), Transformer - like (e.g. Llama), Multi - modal LLMs (e.g. LLaVA)	x86 64 CPU, Apple MPS, NVIDIA GPU, ARM CPU	W fp8 A fp8, W int8 A int8	int4, int8	fp16, int2, int4, int8	tensor - wise, token - wise, channel - wise, group - wise(128)	HuggingFace
OpenVINO	AWQ, GPTQ, SmoothQuant	Mixture - of - Expert (e.g. Mixtral), Transformer - like (e.g. Llama), Multi - modal LLMs (e.g. LLaVA)	x86 64 CPU, Intel GPU, NVIDIA GPU	W int8 A int8	int4, int8	fp16, fp8, int8	tensor - wise, channel - wise, group - wise(32, 64, 128)	Intel
ONNX - Runtime	GPTQ, HQQ, RTN	Mixture - of - Expert (e.g. Mixtral), Transformer - like (e.g. Llama), Multi - modal LLMs (Phi)	x86 64 CPU, NVIDIA GPU	W int8 A int8	int4	fp16	tensor - wise, token - wise, channel - wise, group - wise(32, 128)	Microsoft
PowerInfer	-	Mixture - of - Expert (e.g. Mixtral), Transformer - like (e.g. Llama), Multi - modal LLMs (e.g. LLaVA)	AMD GPU, NVIDIA GPU, x86 64 CPU, Apple M CPU	fp16	int2, int3, int4, int5, int6, int8	fp16	group - wise(32, 256)	Shanghai Jiao Tong University
PPLNN	-	Mixture - of - Expert (e.g. Mixtral), Transformer - like (e.g. Llama)	NVIDIA GPU	W int8 A int8	int8	fp16, int8, int4	token - wise, channel - wise, group - wise(128)	OpenMMLab & SenseTime
Xorbits Inference	AWQ, GPTQ	Multi - modal (Yi - VL), Transformer - like (e.g. Llama), Mixture - of - Expert	CPU, Apple Metal, NVIDIA GPU	fp16	int2, int3, int4, int5, int6, int8	fp16	group - wise(32, 256)	Xorbits
bitsandbytes	LLM.int8()	Mixture - of - Expert (e.g. Mixtral), Transformer - like (e.g. Llama)	AMD GPU, NVIDIA GPU, x86 64 CPU	W int8 A int8	int2, int4, int8, fp8	fp16	channel - wise	HuggingFace
DeepSpeed - MII	FP6 - LLM, ZeroQuant	Mixture - of - Expert (e.g. Mixtral), Multi - modal LLMs (e.g. LLaVA), Transformer - like (e.g. Llama)	NVIDIA GPU	W int8 A int8	fp6	fp16	token - wise, channel - wise	Microsoft
vLLM	AQLM, AWQ, GPTQ, SmoothQuant, SqueezeLLM	Mixture - of - Expert (e.g. Mixtral), Multi - modal LLMs (e.g. LLaVA), Transformer - like (e.g. Llama)	AMD GPU, NVIDIA GPU, TPU, XPU, x86 64 CPU, AWS Neuron	W fp8 A fp8, W int8 A int8	int4, int8, fp6	fp16, fp8	tensor - wise, channel - wise, token - wise, group - wise(32, 64, 128)	University of California, Berkeley
ctransformers	ExLlama, GPTQ	Transformer - like (e.g. Llama)	AMD GPU, NVIDIA GPU	fp16	int2, int3, int4, int5, int6, int8	fp16	group - wise(32, 256)	Ravindra Marella
MLC - LLM	-	Transformer - like (e.g. Llama), Multi - modal LLMs (e.g. LLaVA), Mixture - of - Expert	AMD GPU, NVIDIA GPU, Apple Metal, Intel GPU, Mobile GPU	W fp8 A fp8	int3, int4, int8	fp16	tensor - wise, channel - wise, group - wise(32, 40, 128)	MLC
LMDeploy	AWQ, GPTQ	Mixture - of - Expert (e.g. Mixtral), Multi - modal LLMs (e.g. LLaVA), Transformer - like (e.g. Llama)	NVIDIA GPU, NVIDIA Jetson	W int8 A int8	int4	int4, int8	tensor - wise, token - wise, channel - wise, group - wise(128)	Shanghai AI Lab
LightLLM	AWQ, GPTQ	Mixture - of - Expert (e.g. Mixtral), Transformer - like (e.g. Llama), Multi - modal LLMs (e.g. LLaVA)	NVIDIA GPU NVIDIA Jetson	W int8 A int8	int4, int8, fp6	fp16, int8	token - wise, channel - wise, group - wise(128)	SenseTime
QServe	QoQ	Mixture - of - Expert (e.g. Mixtral), Transformer - like (e.g. Llama), Multi - modal LLMs (e.g. LLaVA)	NVIDIA GPU	W int4 A int8, W int8 A int8	fp16	fp16, int8, int4	tensor - wise, token - wise, channel - wise, group - wise(128)	MIT EECS
llama.cpp	AWQ	Mixture - of - Expert (e.g. Mixtral), Multi - modal LLMs (e.g. LLaVA), Transformer - like (e.g. Llama)	AMD GPU, NVIDIA GPU	fp16	int2, int3, int4, int5, int6, int8	fp16	group - wise(32, 256)	ggml
llama2.c	-	Transformer - like (e.g. Llama)	NVIDIA GPU, Intel CPU, ARM CPU	fp16	int8	fp16	group - wise	Andrej Karpathy
inferflow	AWQ	Mixture - of - Expert (e.g. Mixtral), Transformer - like (e.g. Llama)	NVIDIA GPU, x86 64 CPU, ARM CPU	fp16 only	int2, int3, int4, int5, int6, int8	fp16	group - wise(32, 256)	InferFlow
ScaleLLM	-	Mixture - of - Expert (e.g. Mixtral), Transformer - like (e.g. Llama)	NVIDIA GPU, x86 64 CPU	fp16	int4	fp16	channel - wise, group - wise(32, 64, 128)	Vectorch
SGLang	AWQ, GPTQ	Mixture - of - Expert (e.g. Mixtral), Transformer - like (e.g. Llama), Multi - modal (e.g. LLaVA)	NVIDIA GPU	W fp8 A fp8, W int8 A int8	int4, int8, fp6	fp16, fp8	tensor - wise, channel - wise, token - wise, group - wise(32, 64, 128)	LMSYS
gpt - fast	GPTQ	Mixture - of - Expert (e.g. Mixtral), Transformer - like (e.g. Llama)	AMD GPU, NVIDIA GPU	fp16	int4, int8	fp16	channel - wise, group - wise	Pytorch
FastChat	AWQ, GPTQ	Transformer - like (e.g. Llama)	AMD GPU, Metal, NVIDIA GPU, Intel XPU, Ascend NPU	fp16	int4	fp16	group - wise(128)	LMSYS
OpenLLM	AWQ, GPTQ, SqueezeLLM	Mixture - of - Expert (e.g. Mixtral), Transformer - like (e.g. Llama)	AMD GPU, NVIDIA GPU	fp16	int4	fp16	group - wise(128)	BentoML

表2 量化大语言模型的推理框架

 3.1.1 即用型算法

随着大语言模型量化算法的出现，一些典型方法已被集成到大多数框架中，而有些方法可能最初在特定框架中开发和发布。我们在表2中列出了每个主流框架中最常用的算法。一些方法被大多数框架采用，如GPTQ（弗兰塔尔等人，2022）、AWQ（林等人，2024a）、SmoothQuant（肖等人，2023）等。这些方法具有几个优点：量化后精度高、性能高效、能无缝集成到现有实现流程中，并且用户友好。

此外，一些算法得到多个框架的支持。例如，LLM.int8()（德特默斯等人，2022b）在bitsandbytes（HuggingFace中）得到了很好的支持，它允许直接从HuggingFace Hub存储和加载8位权重，并将线性层中的权重量化为8位。FP6 - LLM（夏等人，2024）集成在DeepSpeed - FastGen中，用于实现6位浮点仅权重量化的运行时量化。它通过统一的配置选项实现6位权重的大语言模型的高效量化和反量化。值得注意的是，Transformers（由HuggingFace开发）和QServe（由MIT EECS的林等人，2024b开发）集成了大多数算法，并提供了全面的用户手册和详细示例，便于深度学习研究人员和开发人员快速上手。

 3.1.2 比特宽度支持

比特宽度的支持通常反映了推理框架或引擎对量化系统实现的全面程度。根据其在加速大语言模型中的位置和功能，可分为三类：

• 仅权重比特：意味着仅对权重进行量化，同时保持激活值为FP16（林等人，2024a）。量化后的权重将使用预先获得的缩放因子反量化回FP16，然后与FP16激活值进行FP16矩阵乘法（mma）。因此，它理论上支持任意比特宽度的非均匀量化。通过减少计算设备与存储主机之间的数据传输延迟（因为权重数据量较小）来实现加速，但权重的反量化会消耗额外的时间。详细的加速效果将在3.2.1节讨论。
• 权重和激活比特：意味着算法同时对权重和激活进行量化，并在底层进行低比特矩阵乘法（MatMul）（例如，在NVIDIA GPU的PTX ISA 8.5中，指令mma.sync.aligned.shape.row.col.s32.u4.u4.s32表示乘数的数据类型是4位无符号整数）。所有框架都支持INT8和FP16矩阵乘法。然而，受硬件计算能力和指令集支持操作的限制，只有部分框架具有INT4和FP8矩阵乘法功能。很少有框架支持不同比特宽度的权重和激活（如\(W_{int 4} A_{int8 }\)），这需要使用汇编的通用矩阵向量乘法（GEMV）指令自定义计算内核（埃吉亚扎里安等人，2024a）。需要注意的是，如果要使用低比特矩阵乘法，硬件架构必须支持特定的低比特计算，并且需要将驱动程序升级/降级到相应版本，以实现真正的低比特计算并获得期望的加速比。
• KV缓存比特：列出了键值（Key - Value，KV）缓存的比特宽度。作为一种缓存技术，随着批量大小和序列长度的不断增加，KV缓存的内存消耗会迅速增长，可能超过模型大小。因此，对KV缓存进行量化可以显著减少模型推理期间的内存使用。有几项工作致力于对KV缓存进行量化（胡珀等人，2024；岳等人，2024；刘等人，2024c）。与仅权重量化算法类似，量化后的键值对通常需要在矩阵乘法前反量化为浮点数，否则需要特定的系统支持低比特与浮点数的乘法。除了列出的比特宽度，所有框架都支持FP16的KV缓存，这意味着直接存储激活值。

我们还列出了量化粒度。用户应参考手册，确保量化粒度应用于权重、激活或KV缓存。我们整理了每个框架的粒度支持情况，作为选择适合实现所需计算内核框架的参考。

 3.1.3 目标平台

众多厂商在深度学习硬件领域竞争激烈。作为当今深度学习GPU领域的先驱之一，NVIDIA GPU得到了大多数框架的支持。同时，vLLM、bitsandbytes、llama.cpp、ctransformers、MLC - LLM和PowerInfer也支持AMD GPU。对于一些其他处理单元，如TPU、XPU、Metal和其他硬件，系统支持相对有限。一些致力于将大语言模型推广到边缘设备的框架更有可能扩展对这些平台的支持，如MLC - LLM、ONNX - Runtime和llama.cpp。然而，需要注意的是，表5中支持低比特量化和硬件部署的框架不能保证任何量化模型都能在列出的每个硬件上进行部署。用户应仔细参考手册获取指导。不过，我们编制的表格可能有助于减少寻找可能满足部署需求的合适框架所需的时间。

 3.1.4 模型家族

所有框架都支持自定义模型定义，并能无缝集成外部模型库，如HuggingFace Hub。为了帮助用户快速上手，框架为常用模型提供了预定义的规范文件。我们大致可以将大模型分为三类：类Transformer大语言模型（如Llama、Orion、Baichuan、ChatGLM、Falcon）、混合专家模型（如Mixtral、Mistral、DeepSeek）、多模态大语言模型（如LLaVA）。然而，并非外部模型库中包含的所有大模型都能得到顺利支持，因为框架集成新算法存在滞后性。因此，用户应参考框架提供的模型库，并确保在从外部模型库导入超出支持模型列表的新模型之前，目标模型没有额外的底层系统要求。

 3.2 量化系统支持

在实际实现中，令人困惑的是，一些量化算法虽然降低了权重或激活的比特宽度，但并没有加快推理速度。因此，一个关键问题浮现出来：量化究竟如何实现真正的加速和存储节省？为了回答这个问题，我们首先需要明确模型推理中涉及的数据传输过程。

图4概述了权重和激活在多级缓存系统中的数据传输过程，展示了量化大语言模型的一般数据流。GPU通常采用具有多个级别的分层缓存结构，每个级别具有不同的大小和输入输出速度。片上缓存（L2缓存、共享内存和寄存器）提供更快的访问速度，但容量有限，而片外缓存（设备内存或全局内存、主机内存）提供更大的容量，但访问速度较慢。因此，在当今的大语言模型推理框架中，我们需要以高度并行的单指令多线程（SIMT）范式分段加载和计算数据，以确保可接受的推理速度。
 主机内存→设备内存：对于权重，我们将一层的权重从主机内存加载到设备的全局内存。带宽相对较低，每个方向为25GB/s（以NVIDIA A100为例，史密斯，2020）。如果进行了量化，权重通常采用紧凑格式，因此可以节省时间。激活值在推理期间最初在设备上生成，不需要从主机复制。
 片外内存→片上内存：我们将准备进行矩阵乘法的一部分权重和激活值从片外全局内存复制到片上L2缓存和共享内存。一次复制的数据量基本上由矩阵乘法（MatMul）内核的设计决定，通常是SIMT在一次内核执行中计算的元素数量的倍数。在A100中，带宽为1555GB/s。
 共享内存→寄存器：为了更快地计算，量化/反量化操作和矩阵乘法通常在寄存器中进行。因此，我们需要将权重和激活值以小块的形式从共享内存复制到寄存器。带宽为19400GB/s，这需要比PCIe多10倍以上的线程数和1/780的计算强度。
 卸载（寄存器→共享内存→片外内存）：计算结果被复制或累加到共享内存的相应元素中。完成对该数据块的计算后，共享内存上的结果被卸载到片外内存。在移动到下一个数据块之前，可以释放存储上一个数据块权重和激活值的内存。

以上，我们以线性层的矩阵乘法为例，明确了数据传输过程。只有在此之后，我们才能回答这个问题：量化如何减少延迟和存储？为了实现实际的推理加速和存储节省，我们需要从底层到高层的量化系统全面支持。

在以下部分，我们根据作用范围展示量化的系统支持：仅权重量化、权重和激活量化、KV缓存量化以及量化和反量化。我们首先介绍大多数框架中的常见通用做法。虽然这些做法可能不是最有效的，但它们具有高可扩展性和通用性，允许快速轻松地集成新算法和实现。然后，我们介绍几种自定义设计。这些研究调查了加速和生成质量的瓶颈，并针对特定范围提出了更快的解决方案。图5展示了权重或激活的量化如何减少推理时间（以4位整数量化为例，也可以是任何其他低比特数据格式）。图6说明了量化的KV缓存如何影响推理。两个图中的加速时间线都根据与FP16相比的时间消耗，将整个过程清晰地分为三类：加速（绿线）、减速（深灰色线）和无影响（浅灰色线）。

图4 推理期间缓存系统中权重和激活的数据传输。带宽和延迟以NVIDIA A100官方报告的数据为例

这张图展示了NVIDIA A100中数据从主机（Host）到设备（Device），再到矩阵乘法内核（MatMul Kernels）的传输路径及相关内存层级结构，具体如下：
 数据传输层级及参数
Host与Device（Off - chip）间：

•     - 通过PCIe连接，带宽为25GB/s ，延迟为1470ns。主机内存（Host Memory）中的数据（如权重 \( W_{FP} \) ）传输到设备的全局内存（Global Memory，容量80GB ）。
• Device（Off - chip）内部：
•     - 全局内存（Global Memory）到二级缓存（L2 Cache，容量40MB ），带宽1555GB/s ，延迟404ns。
•     - L2 Cache到共享内存（Shared Memory，容量256KB ） ，带宽4000GB/s ，延迟150ns。
• Device（On - chip）内部：
•     - 共享内存（Shared Memory）到寄存器（Registers，FP类型 ） ，通过ldmatrix和lds指令传输，带宽19400GB/s ，延迟27ns 。寄存器中的数据最终进入矩阵乘法内核（MatMul Kernels）进行计算。

 数据传输路径
权重数据 \( W_{FP} \) 路径：从主机内存出发，经PCIe传输到设备的全局内存，再依次经过L2 Cache、Shared Memory，最终到达寄存器，进入MatMul Kernels。
激活数据 \( X_{FP} \) 路径：也可从全局内存出发，经L2 Cache、Shared Memory，到达寄存器，进入MatMul Kernels 。此外，还存在异步复制（Async_Copy）路径，用于激活数据在不同层级间的传输。

图中数据体现了不同内存层级间的数据传输带宽和延迟差异，反映了NVIDIA A100内部数据传输的架构和性能特点 ，有助于理解在GPU上进行矩阵乘法运算时数据的流动过程和效率瓶颈所在。

 3.2.1 仅权重量化

在大模型出现前后，模型推理的基本瓶颈都是数据传输和存储成本，这在普通小模型中常常被忽视。由于数据量巨大，传输延迟不容忽视，甚至超过计算延迟，成为大语言模型推理的主要挑战。因此，仅权重量化应运而生，它压缩权重并减轻了各级缓存之间的数据复制负担（林等人，2024a；弗兰塔尔等人，2022）。

仅权重量化相关的过程如图5（a）和（b）所示。仅权重量化和权重与激活量化都需要事先将权重打包为较低比特宽度。权重打包仅在推理前进行一次，消耗的计算资源和时间很少。权重数据被分配到多个线程，每个线程根据以下步骤处理一块数据：（1）通过预先获得的缩放因子将权重量化为较低比特宽度；（2）将它们密集地打包到uint32单元中，没有空闲比特；（3）卸载并存储到主机内存中。因此，与浮点权重相比，打包后的权重在存储上有显著减少。

见图5（b）中的加速时间线，仅权重量化通过减少数据量减轻了从主机内存到片上内存的数据传输负担。然而，由于通用内核仅接受相同数据类型的输入，它在进行矩阵乘法之前引入了额外的权重反量化。只要反量化所花费的时间短于数据传输节省的时间，仅权重量化就能带来加速效果，实际情况确实如此。正是大语言模型中参数传输的过载，使得仅权重量化在实践中具有价值。因此，即使使用浮点矩阵乘法内核，仅权重量化仍然可以加速大语言模型的推理。

对于自定义设计，由于仅权重量化将权重反量化回FP16，在量化权重准备期间可以用任意比特宽度打包权重。许多工作提出了3位、5位、6位权重量化（施等人，2024；弗兰塔尔等人，2022；夏等人，2024）。此外，由于量化后的权重在矩阵乘法前必须反量化到更高比特宽度，因此不必设计从低比特数到实值的线性映射。换句话说，我们可以将整数映射到任意浮点数，并采用查找表进行反量化（多策尔等人，2024a；德特默斯等人，2024）。为了充分利用存储并减少推理期间权重反量化的时间，研究人员在特定平台上设计了自定义后端以支持高效推理。例如，FP6 - LLM（夏等人，2024）设计了完整的GPU内核，以支持更快的FP6→FP16反量化和权重的密集存储。SpQR（德特默斯等人，2023）具有基于GPU的高效解码后端，通过稀疏量化处理异常值并实现负载均衡。

图5 量化的数据传输过程：（a）量化权重准备（权重打包）；（b）仅权重量化；（c）权重和激活量化

这组图展示了量化过程中权重打包、仅权重量化和权重与激活量化的流程 ：
 （a）Prepare (pack weight)
数据传输：权重 \( W_{FP} \) 从主机内存（Host Memory）经PCIe传输到全局内存（Global Memory），再到共享内存（Shared Memory） 。
量化与打包：在共享内存中对 \( W_{FP} \) 进行量化，获取量化参数 \( s_w \) ，得到量化后的 \( W_Q \)（以int32表示 ）。以4比特量化为例，通过移位等操作将 \( W_Q \)（int32）转换为 \( W_Q \)（uint4） ，并打包存储。最终打包后的 \( W_Q \)（uint32）经PCIe返回主机内存，可实现约8倍存储节省。

（b）Process of weight - only quantization
数据传输：打包后的量化权重 \( W_Q \)（uint32）从主机内存经PCIe传输到全局内存，再到共享内存，激活值 \( X_{FP16} \) 也传输到共享内存 。
反量化与计算：在寄存器中，量化权重 \( W_Q \) 经多线程并行反量化，与缩放因子 \( s_w \) 运算后变回 \( W_{FP16} \) 。然后 \( W_{FP16} \) 与 \( X_{FP16} \) 进入浮点矩阵乘法内核（FP MatMul Kernels ）进行计算，计算结果经寄存器、共享内存等返回全局内存 。图中还标注了加速、减速和无影响的时间线。

（c）Process of weight & activation quantization
数据传输：打包后的量化权重 \( W_Q \)（uint32）和量化参数 \( s_w \) 从主机内存经PCIe传输到全局内存，激活值 \( X_{FP16} \) 也传输到全局内存，再到共享内存 。
量化与计算：在寄存器中，对 \( X_{FP16} \) 进行多线程并行量化，得到 \( X_Q \)（uint4） 。之后 \( X_Q \) 与量化权重 \( W_Q \) 进入整数矩阵乘法内核（INT MatMul Kernels ）进行计算，计算结果经寄存器转换等操作，最终经共享内存返回全局内存 。同样标注了加速、减速和无影响的时间线。

这些图详细呈现了不同量化方式下数据在内存层级间的传输、量化及计算过程，有助于理解低比特量化在实际运算中的工作机制 。

 3.2.2 权重和激活量化

遵循传统的量化实践，权重和激活都被量化为低比特宽度，并且矩阵乘法内核也由低比特指令实现。我们在图5（c）中展示了加速时间线，加速的过程包括缓存系统中的权重传输以及低比特矩阵乘法。额外的操作是在矩阵乘法之前将激活从FP16量化为低比特整数，以及在矩阵乘法之后将结果从INT32转换为FP16的数据类型转换。与仅权重量化相比，权重和激活量化能产生更大的加速效果，因为计算密集型的矩阵乘法通常可以通过更低比特宽度的内核加速，这些内核使用更高效的指令和更高的并行度。同时，建议简化激活量化的复杂度，以最小化运行时量化所花费的时间。然而，实际的加速比在很大程度上取决于硬件设计，例如浮点和整数处理单元的数量。

至于定制设计，有两类技术：（1）更快的量化和反量化（或数据类型转换）。例如，QQQ（Zhang等人，2024d）提出了更快的FP16→INT8激活量化、INT4→INT8权重反量化以及INT32→FP16矩阵乘法结果转换，以加速推理过程中的数据格式转换。这项工作基于Kim等人（2022），他们首次引入了更快的INT4→FP16数据类型转换。除了加速，其他方法则试图去除该过程。Tender（Lee等人，2024b）提出了一种分解量化技术，以消除推理过程中的运行时反量化/量化。（2）更快的矩阵乘法内核。通用矩阵向量乘法（GEMV）在适应各种比特宽度方面比通用矩阵乘法（GEMM）更灵活、高效，甚至可以接受具有两种比特宽度的输入矩阵，如INT1INT8和INT3INT8（Wang等人，2023）。通过组合矩阵与向量的几个乘积，我们可以在不填充或产生空闲比特的情况下获得所需结果。例如，EETQ引入的GEMV算子比GEMM内核快13 - 27%。SqueezeLLM（Kim等人，2023）提出了基于查找表（LUT）的GEMV矩阵乘法，在不支持整数矩阵乘法指令的硬件架构上支持高效的4比特矩阵乘法内核。AQLM（Egiazarian等人，2024a）设计了W1A16和W2A8矩阵乘法内核，以直接接收极低比特宽度的输入矩阵并进行计算，而无需反量化或数据类型转换。

 3.2.3 KV缓存量化

KV缓存（即键值缓存）用于优化逐词预测文本令牌的生成模型。尽管模型每次仅生成一个令牌，但每个令牌都依赖于先前的上下文。为避免重复计算，KV缓存作为存储先前键值结果的内存库，以便在后续生成中重用。然而，其存储量高度依赖于序列长度、隐藏层大小、注意力头数量等因素。量化是一种有效的压缩存储方法。整个过程如图6所示。

KV缓存随着序列化输入数据在运行时生成和更新。在推理过程中，来自线性层的\(K_{new}\)和\(V_{new}\)首先被量化，然后连接到已存储的量化键值列表末尾，形成新的列表。当缓存大小超过其限制时，最早的键值对将被丢弃。然后，在使用新生成的查询\(Q_{new}\)进行多头注意力前向传播之前，将矩阵反量化为FP16。我们在加速时间线中展示了KV缓存量化对推理的影响。与FP KV缓存相比，量化后的KV缓存占用更少的设备内存，并且由于数据字节数较小，在缓存系统中的KV数据传输时间也更短。

主要有三种量化KV缓存的技术：（1）量化为更低比特宽度。QoQ（Lin等人，2024b）将KV压缩为4比特，并提出了SmoothAttention以防止因低比特宽度导致的精度下降。KIVI（Zirui Liu等人，2023）甚至开发了一种无需调优的2比特KV缓存量化算法。Yang等人（2024）提出了一种混合精度策略，将最早的KV量化为较低比特宽度，同时为新的KV保留更多比特。（2）量化窗口。许多研究推迟对KV对的量化，仅在全精度KV列表长度超过窗口大小时，对一批数据进行量化。（3）跳过\(K_{new}\)的反量化。像WKVQuant（Yue等人，2024）这样的方法将FP\(K_{new}\)和\(V_{new}\)连接到反量化后的\(K_{prev}\)和\(V_{prev}\)，在K和V矩阵中保留当前令牌的更多信息，然后在满足条件时对\(K_{new}\)和\(V_{new}\)进行量化并存储到KV缓存中。（4）优化异常值。KV矩阵中存在词元级异常值，因此诸如用更高比特宽度存储异常值或减轻异常值幅度等方法可以提高性能（Dong等人，2024；Liu等人，2024c；Kang等人，2024；Lin等人，2024b）。我们省略此类别的详细内容，因为其一般做法与整个模型的量化方法类似。

图6 KV缓存量化示意图

这张图展示了多头注意力（Multi - Head Attention）机制中涉及量化操作的流程，以及对数据传输和存储的影响 ，具体如下：
 模块输入与量化
输入层：分别有三个线性层 \( Q\_Linear \)、\( K\_Linear \)、\( V\_Linear \) ，对应产生查询（Query）、键（Key）、值（Value）相关数据。其中 \( K\_Linear \) 和 \( V\_Linear \) 输出的数据会经过量化（Quantize）操作 。
 缓存机制与数据更新
缓存模块：存在 \( K \) Cache 和 \( V \) Cache ，分别存储之前的键值对 \( K\_prev \) 和 \( V\_prev \) 。新生成的 \( K_{new} \) 和 \( V_{new} \) 会与缓存中的数据进行合并更新。例如，从 \( K \) Cache 中取出索引为 \( [0:L - 1] \) 的数据，与新的 \( K_{new} \)（索引为 \( [L] \) ）合并 ；\( V \) Cache 同理。在这个过程中，还涉及数据的丢弃（drop）操作。
 量化与反量化
量化与反量化操作：量化后的 \( K \)（\( K_{INT} \) ）会经过反量化（Dequantize）变回 \( K_{FP} \) ，与未经过量化的 \( Q_{FP} \) 以及量化后再变回浮点形式的 \( V_{FP} \) 一起进入多头注意力前向传播（Multi - Head Attention Forward）模块进行计算 。
 性能影响标注
右侧时间线：图右侧标注了不同操作对速度的影响，绿色表示加速（Speedup），灰色表示减速（Slow down），浅灰色表示无影响（Not affect） 。同时指出这种量化方式能够实现更快的数据传输（Faster data transmission）和更少的存储占用（Less storage） 。

整体而言，该图呈现了多头注意力机制中结合量化操作的运行流程，以及其在性能优化方面的特点 。

 3.2.4 量化和反量化

在本节中，我们大致将量化分为三类：（1）浮点数量化，将高比特浮点数转换为低比特浮点数。（2）整数量化，主要指将浮点数划分为等间距的整数。这里我们省略将高比特宽度整数重新量化为低比特宽度的情况，因为在实际应用中很少使用，并且很少有研究提出更快的整数转换实现。（3）二值化，包括符号函数和布尔函数。
 浮点数量化：将高比特宽度浮点数量化为低比特宽度实际上是对尾数比特的裁剪。这是因为与低比特宽度的目标值相比，高比特宽度的源值通常在指数和尾数部分具有更多或相等的比特数。算法3.2.4给出了将FP32量化为FP8的示例。我们遵循Micikevicius等人（2022）总结其一般过程如下：
    缩放：由于目标值占用更少的比特宽度，其表示范围可能会大幅缩小，无法传达大部分数据。将源值缩放到合适的范围可以在量化为FP8后最好地保留信息。缩放因子通过学习或校准预先获得。
    检查溢出/下溢：检查源值是否超出FP8范围的上限或下限。如果是，则直接返回最大值或最小值。如果未溢出，则检查指数部分是否低于FP8格式可以表示的最小正规格化数。如果是，我们将该值除以FPx中的最小非规格化数，四舍五入到最接近的整数，然后乘以最小非规格化数。该整数确定尾数比特的值，指数比特全部设置为零。
    复制和舍入：如果值既未超出FP8的范围也未下溢，我们从源FP32值中复制较低的e比特到目标FP8值。然后通过四舍五入将尾数裁剪为m比特。值得注意的是，舍入和溢出/下溢处理在实际应用中对于保持数值稳定性和精度都至关重要。然而，由于尾数比特的减少，在转换为较低比特宽度时精度下降是不可避免的。
 浮点反量化：将浮点数反量化为更高比特宽度很直接。在FP格式系统中，低比特宽度值的指数和尾数比特宽度都不会超过高比特宽度值。因此，我们可以直接从原始值（比特数较少）中提取并复制符号位、指数和尾数到目标值（比特数较多）相应部分的最高有效位。然后对指数和尾数部分的其余比特进行零填充。
 整数量化：我们首先通过除以缩放因子\(s \in \mathbb{R}^{+}\)将浮点数缩放到INTk的表示范围，并加上零点\(z \in \mathbb{Z}\)来移动夹紧范围（Wu等人，2020）。round()是四舍五入函数，clamp(\(\cdot, q^{min }, q^{max }\))将值限制在k比特的表示范围内，在对称量化中\(q^{max } = 2^{k - 1}-1\)，在非对称量化中\(q^{min } = 0\)，\(q^{max } = 2^{k}-1\)。因此，整体量化公式可以写为：
\(X_{INT_{k}}=clamp\left(round\left(\frac{X_{FP}}{s}\right)+z, q^{min}, q^{max}\right)\)
其中，缩放因子s可以初始化为\(s_{0}=(q^{max } - q^{min }) / (X_{FP}^{max } - X_{FP}^{min })\)，\(X_{FP}^{max }\)和\(X_{FP}^{min }\)是最大值和最小值。

对于系统支持，许多框架将Marlin量化（Frantar和Alistarh，2024）作为标准过程。伪代码算法2概述了Marlin量化的步骤，并以4位整数量化为例。值被量化并存储为具有所需比特宽度的无符号整数。将进行额外的预/后移位以获得有符号值。因此，我们首先通过s缩放\(X_{FP 32}\)值并将其舍入为整数。然后，加上\(2^{k - 1}\)将值移动到uINT4（4位无符号整数）范围内的非负整数。我们省略C++内置数据类型转换函数float2uint的细节。为便于理解，我们通过双重for循环解释第4到8行的打包过程，实际实现为第9到11行。在4位量化中，每8个值被打包为一个uINT32，量化后的矩阵大小是原始的四分之一。通过使用\(i::8\)，我们沿着维度C从i开始提取每8个值，每次增加8，默认结束（直到维度C的末尾）。然后将值左移\(4  i\)，将4位值放置到相应的比特范围，在右侧留下\(4  i\)个零，以便在进行或运算后保留先前存储的量化值。

有几种自定义算法引入了更快的数据类型转换。QQQ（Zhang等人，2024d）设计了一种更快的FP16到INT8转换，名为FastFP16toINT8。它首先将FP16值加上128，移动到uINT8的表示范围。接着，再加上1024，有效地将uINT8的8位转换并放置到FP16尾数的较低段。最后，从FP16中提取较低的8位，并与0x80进行异或运算，得到所需的INT8格式。在实践中，整个过程可以进一步简化为融合乘加（FMA）、排列（PRMT）和异或操作。
 整数反量化：指通过乘以缩放因子将整数投影回实数，可以表示为：
\(\hat{X}_{FP}=s \cdot\left(X_{INT x}-z\right) \approx X_{FP}\)
因此，在许多工作中，s也可以通过从候选值中搜索来初始化，以找到最优值（Wei等人，2023b）：
\(s_{candidate }=\frac{i}{num_{i}} s_{0}, i \in \mathbb{Z}^{+}, i \in\left(0, num_{i}\right)\)
\(s.t. min \left\| X_{FP}-\hat{X}_{FP}\right\| _{p}\)
其中\(num_{i}\)表示候选值的数量，通常设置为50、100等（Yuan等人，2024；Wei等人，2023b）。s也可以是一个可学习的参数（Wei等人，2023b；Shao等人，2023）。在大语言模型出现之前，寻找更好的s的方法就已经得到了广泛研究（Ding等人，2024；Wei等人，2023a）。

对于系统支持，我们首先根据打包方式解包元素，然后将它们乘以相应的缩放因子，缩放因子可以是张量级、通道级、词元级等2.2节中描述的粒度。也提出了自定义实现，SINT4toS8 Li等人（2023a）设计了一种通过乘以16实现更快的INT4到INT8转换的方法。
 二值化：采用符号或布尔函数提取符号：
\(X_{sign}=\left\{ \begin{array}{ll} {1,}&{X_{FP} \geq 0, \\ -1, & X_{FP}<0, \end{array} X_{bool}=\left\{ \begin{array} {ll}{1,}&{X_{FP} \geq 0,}\\ {0,}&{X_{FP}<0.}\end{array} \right. \right.\)
使用符号函数还是布尔函数取决于算法设计，即我们期望比特代表什么值。例如，二值化Transformer通常在注意力分数和ReLU激活后使用布尔函数，而线性函数中的权重和激活采用符号函数。由于硬件通常将比特视为0或1，我们可以组合指令来实现任何期望的矩阵乘法。例如，在NVIDIA GPU上，mma指令将0/1比特矩阵视为0和1进行按位累加操作（popcount）。因此，为了获得正确的累加结果，popcount函数设计了不同的算术规则，即如果每次遇到0就减去1，我们可以得到符号函数的结果。它有许多加速实现，如查找表、nifty popcnt（Wilkes等人，1958）、hacker popcnt（Warren，2012）、hakmem popcnt等。
 二值化反量化：只需乘以缩放因子s，即\(\hat{X}_{FP}=s \cdot X_{sign / bool }\)以保留原始值的大小。很容易理解，二值化会丢失大量信息。因此，由于性能急剧下降，很少有研究致力于二值化大语言模型。由于显著的加速和存储减少，深入研究二值化大语言模型是有价值的，但可能需要超越符号和布尔函数的新公式。DB - LLM（Chen等人，2024a）提出通过分解为两个1位权重矩阵进行2位权重量化，理论上在矩阵乘法中效率更高。

 4 高效大语言模型训练的量化策略

 4.1 低比特训练

使用低比特加速大语言模型（LLMs）训练存在多种策略。常用技术包括BF16、FP16、FP8和INT8训练。
 FP16训练：在所有数据格式中，BF16训练广泛应用于大语言模型，因其在训练期间通常较为稳定。然而，这需要诸如A100、4090、H100等具备Ampere或Hopper架构的硬件支持。对于像Volta或Turing架构（如V100、T4）这类较旧的硬件，该数据格式不可用。在这些情况下，FP16常被用于加速训练，甚至一些小型计算机视觉模型也会采用。由于FP16的指数位较少，它面临更高的下溢或溢出风险。因此，提出了损失缩放策略以保留较小或较大的梯度幅度。详细过程如算法3所示。
 FP8训练：鉴于一些硬件供应商（如NVIDIA或AMD）推出了支持FP8或FP4格式的新架构。为在进行少量修改的情况下实现理想的加速效果，我们可利用供应商提供的Transformer Engine库。尽管FP8类型提供的动态范围足以存储特定的激活或梯度，但无法同时满足所有激活和梯度的存储需求。这使得适用于FP16的单一损失缩放因子策略在FP8训练中不再适用，而需要为每个FP8张量使用不同的缩放因子。缩放过程可表示为：
\(FP8\_MAX = maximum\_representable(fp8\_format)\)
\(exp = get\_exponent \left(FP8\_MAX / a_{max}\right)\)
\(new\_scaling\_factor = 2.0^{exp}\)
其中，fp8格式代表如E4M3或E5M2等格式，FP8_MAX是该格式下的相关最大值，\(a_{max}\)是张量的最大绝对值。然后，我们可以用exp计算新的缩放因子。然而，新缩放因子的计算不能在线进行，因为这会导致更多的内存访问。最佳实践是采用延迟缩放策略。该策略依据之前若干次迭代中观察到的绝对值最大值来选择缩放因子，这使得FP8计算能够充分发挥性能，但需要存储最大值的历史记录作为FP8算子的额外参数。在表3中，我们列出了支持低比特浮点训练的流行框架和引擎，包括微软的Deepspeed、英伟达的Megatron - LM和GraphCore的UnitScaling。
 INT8训练：在训练过程中，除了模型的权重参数，还需保存优化器所需的梯度以及权重或梯度的备份信息。这使得大语言模型庞大的参数规模在微调期间成为更为突出的内存瓶颈，限制了它们在更广泛应用场景中的部署。INT8训练（Zhu等人，2020）被视为一种直接减少训练期间梯度内存使用的方法。然而，反向传播中量化的不稳定性使得大语言模型的训练更加不稳定，甚至可能导致崩溃。QST（Zhang等人，2024g）提出同时优化内存使用的三个关键来源：模型权重、优化器状态和中间激活。除了将大语言模型的权重量化为4比特，并引入一个单独的侧网络（该网络使用大语言模型的隐藏状态进行特定任务的预测），QST还采用了几个低秩适配器和无梯度下采样模块，显著减少了可训练参数的数量，从而节省了优化器状态的内存。Q - GaLore（Zhang等人，2024f）指出，GaLore使用奇异值分解（SVD）投影梯度的内存节省策略会带来显著的时间成本。为解决这一问题，Q - GaLore根据梯度收敛统计自适应更新梯度子空间，并将投影矩阵保持为INT4格式，权重保持为INT8格式，使得Llama - 7b能够在单个16GB GPU上从头开始训练。Jetfire（Xi等人，2024）采用INT8数据流来优化内存访问，并使用逐块量化方法来保持预训练Transformer的精度。4 - bit Optimizer（Li等人，2024a）使用较小的块大小，并提出利用行和列的信息来实现更好的量化，还进一步发现了量化二阶矩时的零点问题，并使用线性量化器解决了该问题。

算法3 采用FP16精度的权重更新算法

1. 步骤1：将输入的32位浮点数 \( X_{FP32} \) 除以缩放因子 \( s \)，得到未缩放的32位浮点数 \( X_{unscaled FP32} \) ，即 \( X_{unscaled FP32} = X_{FP32}/s \) 。这一步是为后续的量化操作做准备，通过缩放调整数值范围。
2. 步骤2：计算指数部分的最小值 \( e_{min} \) ，公式为 \( e_{min} = -(1 << (e - 1)) + 1 \) 。这里 \( << \) 是按位左移操作，此步骤确定了低比特浮点数表示中指数部分能取到的最小数值 。
3. 步骤3：计算指数部分的最大值 \( e_{max} \) ，公式为 \( e_{max} = (1 << (e - 1)) \) 。确定了低比特浮点数表示中指数部分能取到的最大数值 。
4. 步骤4：计算一个与精度相关的参数 \( m \) ，公式为 \( m = x - e - 1 \) 。这里 \( x \) 未在给定算法前文中说明含义，推测是与数据特性或量化规则相关的一个值，该参数后续用于处理尾数部分。
5. 步骤5：计算低比特浮点数（FP8 ）理论上指数部分能表示的最大值对应的数值 \( X_{e FP8} \) ，公式为 \( X_{e FP8} = e_{max} + 2^{8 - 1} << 23 \) 。这一步确定了指数部分在理论最大取值下对应的数值，用于后续判断和计算。
6. 步骤6：计算低比特浮点数（FP8 ）理论上尾数部分能表示的最大值对应的掩码 \( X_{m FP8} \) ，公式为 \( X_{m FP8} = ~(0x007FFFFF >> m) & 0x007FFFFF \) 。通过位运算得到与尾数最大值相关的掩码值 。
7. 步骤7：计算低比特浮点数（FP8 ）理论上能表示的最大值 \( X_{theomax FP8} \) ，公式为 \( X_{theomax FP8} = X_{e FP8} + X_{m FP8} \) 。综合指数和尾数的最大值，得到整个浮点数能表示的理论最大值 。
8. 步骤8 - 11：检查是否发生指数溢出。如果未缩放的32位浮点数 \( X_{unscaled FP32} \) 大于 \( clipmax \) 和理论最大值 \( X_{theomax FP8} \) 中的较小值，将结果 \( X_{FP8} \) 设置为 \( clipmax \) 和 \( X_{theomax FP8} \) 中的较小值；如果 \( X_{theomax FP8} \) 小于 \( clipmin \) 和 \( -X_{theomax FP8} \) 中的较大值，将结果 \( X_{FP8} \) 设置为 \( clipmin \) 和 \( -X_{theomax FP8} \) 中的较大值 。这部分通过比较来处理可能超出表示范围的数值，避免溢出错误。
9. 步骤13 - 15：提取未缩放的32位浮点数 \( X_{unscaled FP32} \) 的符号位 \( X_{sign FP8} \) 、指数位 \( X_{e FP8} \) 和尾数位 \( X_{m FP8} \) ，分别通过按位与操作得到，即 \( X_{sign FP8} = X_{unscaled FP32} \& 0x80000000 \) 、\( X_{e FP8} = X_{unscaled FP32} \& 0x7F800000 \) 、\( X_{m FP8} = X_{unscaled FP32} \& 0x007FFFFF \) 。为后续判断和处理做准备。
10. 步骤16 - 18：检查是否发生指数下溢。如果 \( (X_{e FPx} >> 23) - 2^{x - 1} < e_{min} + 1 \) ，计算次规范数 \( X_{min FP8}.subnorm = 1 / (1 << ((1 << (e - 1)) + m - 2)) \) ，然后将 \( X_{FPx} \) 设置为 \( round2int(X_{unscaled FP32} /X_{min FP8}.subnorm)X_{min FP8}.subnorm \) 。这部分处理指数过小的情况，避免下溢错误。
11. 步骤20 - 21：对尾数进行舍入操作。先计算 \( R_m = (X_{m FP8}<<m) \& 0x007FFFFF + 0x3F800000 \) ，然后将 \( R_m \) 进行舍入操作 \( R_m = round2int(R_m - 1) \) 。通过这些操作调整尾数的精度 。
12. 步骤22：进一步处理尾数，公式为 \( X_{m FP8} = (X_{m FP8}>>(23 - m) + R_m)<<(23 - m) \) 。通过位运算和舍入结果进一步调整尾数 。
13. 步骤23：将符号位 \( X_{sign FP8} \) 、指数位 \( X_{e FP8} \) 和处理后的尾数位 \( X_{m FP8} \) 组合起来，得到最终的8位浮点数 \( X_{FP8} \) ，即 \( X_{FP8} = X_{sign FP8} + X_{e FP8} + X_{m FP8} \) 。
14. 步骤25：返回量化后的8位浮点数 \( X_{FP8} \) 。

表3 低比特训练系统

 4.2 针对参数高效微调（PEFT）的量化策略

经过良好预训练的大语言模型具有出色的泛化能力，在微调过程中表现出良好的迁移性和适应性，使其在各种下游任务中具有潜在的应用价值。然而，大语言模型庞大的参数规模在微调期间造成了显著的内存瓶颈，限制了它们更广泛的应用。因此，引入了参数高效微调（PEFT）的概念，以解决资源受限情况下大语言模型的微调问题（Ding等人，2023；Han等人，2024）。

随着大语言模型微调需求的出现，人们发现量化可以减少微调过程中的内存使用；一些方法改进了传统的量化感知训练（QAT），显著降低了每次更新时的参数负载，而另一类方法则将量化与低秩适应（LoRA）微调方法相结合。

 4.2.1 结合量化的部分参数微调

以往的量化感知训练方法所需资源几乎与全参数训练相同，这使得它们在资源受限的微调场景中不可行。因此，提出了部分参数微调策略。PEQA（Kim等人，2024）遵循简单的量化感知训练方法。但在对权重W进行量化后，它获取缩放因子\(s_{0}\)和定点数\(\bar{W}_{0}\)，然后保留W并仅训练\(s_{0}\)。OWQ（Lee等人，2024a）在混合精度量化后仅更新高精度的“弱列”。

 4.2.2 低比特低秩适应

低秩适应（LoRA）（Hu等人，2021）冻结预训练权重，仅训练低秩矩阵。尽管它将可训练参数减少了10,000倍，但并未减小预训练模型权重本身的大小，因此仅将微调的内存需求降低了3倍。

像QLoRA（Dettmers等人，2024）这样的方法利用低比特量化，通过对量化后的大语言模型进行LoRA微调进一步减少内存占用。他们首先使用训练后量化（PTQ）方法将预训练的大语言模型量化为低比特：
\(W_{q} \leftarrow quant(W)\)
其中W是每一层的权重。然后，在微调过程中，他们冻结所有权重参数，仅更新LoRA，前向传播如下：
\(Y = X \cdot dequant(W)+X \cdot A B\)
其中X是每一层的输入。

在这些方法中，矩阵A通常用随机高斯值初始化，而B初始化为全零。这种方法不仅显著减少了模型权重参数的内存占用，还确保了优化器在微调期间仅需存储LoRA的梯度，大大降低了内存使用。QLoRA（Dettmers等人，2024）引入使用Normal Float对W进行双重量化，既实现了良好的精度保持，又节省了内存，使得在单个48GB GPU上对650亿参数的预训练模型进行微调成为可能。IR - QLoRA（Qin等人，2024）将信息论融入QLoRA范式，通过信息校准和连接提高了微调性能。LoRA +（Hayou等人，2024）表明，为LoRA中的矩阵A和B设置不同的学习率能够实现高效的特征学习。QDyLoRA（Rajabzadeh等人，2024）和Bayesian - LoRA（Meo等人，2024）在LoRA中采用了更灵活的秩分配。

此外，一些方法旨在在LoRA微调后获得可部署的量化合并模型。QA - LoRA（Xu等人，2023）使用INT格式对W进行量化，并将\(X \cdot A^{i ×r} B^{r ×o}\)调整为\(mean(X) \cdot A^{\frac{i}{L} ×r} B^{r ×a}\)，使得微调后的AB能够无损地合并到INT格式的\(w_{q}\)中，在部署时无需额外计算。另一方面，L4Q（Jeon等人，2024）保持\(A \in \mathbb{R}^{i ×r}\)的维度，并直接使用完整的量化感知训练前向传播方法，同时更新A、B和W + AB的量化器参数s和b。虽然L4Q在预训练期间没有通过量化减少权重的内存占用，但优化器仍然无需保留权重的梯度，从而得到一个可直接部署且精度更高的微调量化模型。

许多方法已经认识到LoRA的初始化对这些基于量化的参数高效微调方法的有效性有显著影响。因此，它们旨在在微调前最小化\(\left\|W-(W_{q}+A B)\right\|_{F}\)。LoftQ（Li等人，2023c）和LQ - LoRA（Guo等人，2023b）都通过迭代计算实现这一目标：\(Q_{t} \leftarrow quant(W - A_{t - 1} B_{t - 1}^{\top})\)和\(A_{\ell}\)，\(B_{t} \leftarrow S V D(W - Q_{t})\)。LQ - LoRA还建议纳入校准数据，将最小化目标调整为\(\left\|\sqrt{F} \odot(W-(W_{q}+A B))\right\|_{F}^{2}\)，其中F是W的Fisher信息矩阵，\(\odot\)表示Hadamard乘积。此外，LQ - LoRA引入动态量化配置，以更好地适应资源限制。

图7展示了不同的LoRA结构。图7（a）代表像QLoRA这样在微调阶段不改变大语言模型任何部分且保留完整原始LoRA结构的方法（Dettmers等人，2024；Qin等人，2024；Hayou等人，2024；Li等人，2023c）。图7（b）代表像QA - LoRA这样在微调阶段也不改变大语言模型任何部分，但修改原始LoRA结构的方法（Xu等人，2023）。图7（c）代表像L4Q这样修改原始LoRA结构并使用类似于量化感知训练的训练过程的方法（Jeon等人，2024）。（a）和（b）在微调期间仅需要量化后的大语言模型权重\(W_{q}\)，而（c）需要存储预训练的全精度权重\(W_{f p}\)。（a）仅旨在降低训练成本，微调后无法直接生成量化模型，而（b）和（c）在微调后可以直接集成LoRA模块以生成可部署的量化模型。

图7 不同LoRA结构示意图

 5 高效大语言模型推理的量化算法

本节将探讨大语言模型量化的算法。量化算法大致可分为两种主要方法：量化感知训练（QAT）和训练后量化（PTQ）。量化感知训练将量化集成到训练/微调过程中，使模型能够学习并适应量化约束，从而最小化因低精度导致的精度损失。相比之下，在训练后量化场景中，我们给定一个预训练的浮点模型和少量校准数据，旨在无需端到端训练过程即可生成准确的量化模型。我们将详细研究这些量化算法。在本节结束时，我们希望我们的综述能全面系统地收集适用于大语言模型的各种量化算法、它们的实现策略以及对模型性能和效率的影响。

 5.1 量化感知训练

表4总结了大语言模型的不同量化感知训练方法。LLM - QAT（Liu等人，2023b）是探索大语言模型量化感知训练的开创性工作。为克服训练数据的限制，它提出了无数据知识蒸馏，使全精度模型的教师logits与量化模型的学生logits对齐。在LLM - QAT之后，BitDistiller（Du等人，2024）在自蒸馏阶段采用非对称裁剪策略进行非对称量化。EfficientQAT（Chen等人，2024b）通过将量化感知训练分为两个连续阶段，显著降低了训练成本。第一阶段优化每个块的所有参数，然后第二阶段仅优化整个网络的量化参数。为开启极端量化水平的新时代，BitNet（Wang等人，2023）用原始线性层替换了BitLinear层并从头开始训练。其变体BitNet b1.58（Ma等人，2024a）对每个参数使用三值权重，实现了近乎无损的性能。

表4 不同量化感知训练方法的比较

 5.2 训练后量化

训练后量化（PTQ）是一种对预训练模型应用量化的技术。与量化感知训练不同，训练后量化不需要模型在训练时使用量化模块。这使得训练后量化成为部署最初以高精度训练的模型的一种非常实用的方法。当访问训练数据受限或重新训练计算成本高昂时，训练后量化特别有用。因此，随着大语言模型的发展，在过去几年中，训练后量化算法显著增加，因为它们的训练成本较低。

为了更好地介绍，我们系统地将训练后量化算法分为几类，如图8所示。

图8 训练后量化算法概述

 5.2.1 等效变换

许多研究（Luo等人，2020；Bondarenko等人，2021；Wei等人，2023b；Xiao等人，2023）都强调了大语言模型中存在显著的异常值。这些异常值给量化带来了巨大挑战，因为它们迫使大量正常值用有限的比特数表示，从而导致较大的量化误差和精度下降。因此，近年来出现了许多算法，旨在缓解大语言模型中的异常值问题。

在所有解决异常值问题的算法中，等效变换是最具代表性和有效性的方法之一。将等效变换应用于语言模型的开创性工作之一是异常值抑制（OS）（Wei等人，2022）。OS拆分了LayerNorm函数，并将LayerNorm的参数\(\gamma\)迁移，以避免异常值。
\(X_{j}=X_{j}' \cdot \gamma_{j}\)
然后LayerNorm变为非缩放形式，下一层的权重可以吸收\(\gamma\)：
\(W\left(x \odot\left[\begin{array}{c}\gamma_{1} \\ \gamma_{2} \\ \cdots \\ \gamma_{n}\end{array}\right]\right)=\left(W \odot\left[\begin{array}{llll}\gamma_{1} & \gamma_{2} & \cdots & \gamma_{n} \\ \gamma_{1} & \gamma_{2} & \cdots & \gamma_{n} \\ \cdots & & \\ \gamma_{1} & \gamma_{2} & \cdots & \gamma_{n}\end{array}\right]\right) x\)
通过这种方式，OS可以抑制异常值。从OS方法开始，随后出现了许多等效变换技术。大多数等效变换方法通过使权重或激活中的异常值分布更加对称和平滑，来减轻异常值对量化的影响，其公式如下：
\(\begin{aligned} Y & =X W+B \\ & =\left[(X-\Delta) \cdot M^{-1}\right] \cdot[M \cdot W]+(B+\Delta \cdot W), \end{aligned}\)
其中\(\Delta\)是用于使输入中异常值分布对称的移位因子，M是用于使分布更平滑的矩阵。通过采用上述等效变换，许多现有量化方法在各种量化设置和场景下都取得了最先进（SOTA）的性能。

基于实现方式，等效变换可进一步细分为三类：移位变换、缩放变换和旋转变换。我们将分别对每一类进行详细介绍。
 移位变换：大语言模型中的异常值在不同通道上呈不对称分布。这种不对称表示可能导致由小范围通道组成的张量整体范围非常大，从而在量化过程中带来困难。为了解决这个问题，OS +（Wei等人，2023b）首先提出了通道级移位变换，通过如下公式调整通道间的激活，以减轻不对称的影响：
\(\hat{X}=X-\Delta\)
其中\(\Delta \in \mathbb{R}^{c ×1}\)是一个行向量，用于移动激活的每个通道。需要注意的是，此操作不是对称量化中使用的传统移位操作，而是在通道级上进行的，为逐张量量化提供了更好的分布。具体来说，OS + 以手工方式定义\(\Delta\)：
\(\Delta_{j}=\frac{max \left(X_{:, j}\right)+min \left(X_{:, j}\right)}{2}\)
通过通道级移位，张量范围缩小到最大通道范围，消除了不对称异常值的影响。然而，手工设置等效参数会导致次优结果。因此，OmniQuant（Shao等人，2023）被提出，通过最小化块级量化误差以可微的方式确定最优移位参数：
\(arg min _{\Delta}\left\| \mathcal{O}(W, X)-\mathcal{O}\left(Q_{w}(W ; \Delta), Q_{a}(X ; \Delta)\right)\right\| \)
其中\(\mathcal{O}\)表示大语言模型中Transformer块的映射函数，\(Q_{w}(\cdot)\)和\(Q_{a}(\cdot)\)分别表示权重和激活量化器，\(\Delta\)是移位参数。块级最小化易于优化且资源需求最小。因此，通过逐块优化目标函数，可以比OS + 中直接计算更高效、更节省资源地获得更有效的移位向量。然而，OmniQuant需要对可学习参数进行微调，否则容易出现梯度爆炸等问题。与OmniQuant类似，AffineQuant（Ma等人，2024b）也采用基于学习的移位操作。

我们在图9中展示了移位变换的示意图。移位因子\(\Delta\)可以融合到LayerNorm和权重矩阵中，因此无需额外开销。
 缩放变换：移位变换有效地解决了激活中异常值的不对称分布问题，减小了由不对称导致的大数值范围。然而，这仅有助于逐张量量化，并未降低逐通道量化的难度，因为它没有从根本上消除激活中跨通道分布的异常值。为了进一步减少异常值对量化的影响，SmoothQuant（Xiao等人，2023）最初提出使用缩放变换。它基于一个关键观察：尽管由于异常值的存在，激活比权重更难量化，但不同的词元在其通道间表现出相似的变化（Dettmers等人，2022a）。基于这一观察，SmoothQuant通过引入一种数学上等效的逐通道缩放变换，将量化难度从激活转移到权重上，从而显著平滑了通道间的幅度：
\(Y=\left(X diag(\Phi)^{-1}\right) \cdot(diag(\Phi) W)=\hat{X} \hat{W}\)
其中\(\Phi\)是平滑因子。需要注意的是，\(diag(\Phi)\)对应于公式20中的矩阵\(M\)，但它是一个对角矩阵，用于实现逐通道平滑。SmoothQuant引入了一个超参数\(\alpha\)作为迁移强度，以控制从激活到权重迁移的难度大小，使用以下公式：
\(\Phi_{j}=\frac{max \left(\left|X_{j}\right|\right)^{\alpha}}{max \left(\left|W_{j}\right|\right)^{1-\alpha}}\)
然而，这种方法需要多次试验来确定不同模型的最佳迁移强度，例如，\(\alpha = 0.5\)对于所有OPT（Zhang等人，2022）和BLOOM（Le Scao等人，2023）模型来说是一个平衡较好的点。

受SmoothQuant的启发，FPTQ（Li等人，2023b）认为在计算激活平滑尺度时无需考虑权重，而通过非线性无损映射保留所有激活值至关重要。这种映射需要满足两个标准：（1）与正常值温和接触；（2）严厉抑制异常值。基于此，他们采用对数函数来改进平滑矩阵\(\Phi\)的计算：
\(\Phi_{j}=\frac{max \left(\left|X_{j}\right|\right)}{log _{2}\left(2+max \left(X_{j}\right)\right)}\)
除了FPTQ，许多其他工作也遵循了SmoothQuant的方法。OS + 和AWQ（Lin等人，2024a）都使用基于搜索的方法来找到平滑尺度。然而，这两种方法的优化目标和搜索空间不同。OS + 的优化目标是：
\(\Phi^{}=arg min _{\Phi} \mathbb{E}\left\| Q\left((X-\Delta) \cdot diag(\Phi)^{-1}\right) Q\left(diag(\Phi) \cdot W^{\top}\right)+\hat{b}-\left(X W^{\top}+b\right)\right\| _{F}^{2}\)
为了简化搜索空间，OS + 优化异常值阈值\(t\)，将激活范围超过\(t\)的通道压缩到\((-t, t)\)，其他通道保持不变。这将问题简化为单变量问题。然后使用网格搜索来找到使目标最小化的\(t\)。找到最优\(t\)后，缩放向量计算如下：
\(\Phi_{j}=max \left(1.0, \frac{max \left(X_{:, j}-\Delta_{j}\right)}{t}\right)\)
AWQ发现权重通道的显著性实际上由激活尺度决定。为此，它采用激活感知优化目标，并使用非常简单的搜索空间：
\(\Phi=\Phi_{x}^{\alpha}, \alpha^{}=arg min _{\alpha}\left\| Q\left(W \cdot diag\left(\Phi_{x}^{\alpha}\right)\right)\left(diag\left(\Phi_{x}^{\alpha}\right)^{-1} \cdot X\right)-W X\right\| \)
其中\(\Phi_{x}\)是激活的平均幅度（逐通道），并使用单个超参数\(\alpha\)来平衡对显著通道和非显著通道的保护。

除了基于搜索的方法，一些方法使用基于学习的技术来找到最优缩放矩阵。OmniQuant和AffineQuant也学习缩放矩阵。在公式23中，OmniQuant同时学习移位因子\(\Delta\)和缩放矩阵\(diag(\Phi)\)。然而，OmniQuant仅在对角矩阵范围内进行优化。AffineQuant（Ma等人，2024b）认为这种有限的搜索范围可能导致显著的量化误差，降低了量化方法在低比特场景下的通用性。它提出学习一个通用的可逆矩阵，对权重和激活进行等效仿射变换，从而取得更好的结果。

我们也在图10中展示了缩放变换的示意图。与移位变换一样，缩放因子\(\Phi\)可以合并到层归一化（LayerNorm）和权重矩阵中。
 旋转变换：旋转变换最早由QuIP（Chee等人，2024）引入。QuIP基于这样一种见解，即当权重和海森矩阵不相关时，量化效果更好。这意味着权重应具有相似的幅度，并且需要精确舍入的方向不应与坐标轴对齐。简单来说，如果一个权重矩阵满足：
\(max (W) \leq \mu\| W\| _{F} / \sqrt{m n}\)
则称其为\(\mu\) - 不相关的，其中\(mn\)是矩阵元素的数量，\(\|\cdot\|_{F}\)是弗罗贝尼乌斯范数。QuIP表明，在权重矩阵的左右两侧乘以正交矩阵可以降低不相关性，这相当于对权重矩阵进行旋转变换。QuIP使用克罗内克结构的正交矩阵，允许快速进行额外计算。在此基础上，QuIP（Tseng等人，2024a）用哈达玛矩阵替换了这些矩阵，通过更好的不相关性增强了量化效果，并加速了前向传递，因为哈达玛变换可以通过\(O( nlogn )\)次加法运算来计算。

这两种方法都针对仅权重量化。在这些方法的基础上，QuaRot（Ashkboos等人，2024）引入了一种权重和激活量化方法，该方法也对KV缓存进行量化。QuaRot分两个阶段进行操作。第一阶段，对模型权重进行全精度处理，并在模型的前向传递中添加两个哈达玛操作。第二阶段，使用现有方法对权重进行量化，并将量化操作集成到前向传递中，用于在线激活量化。

然而，QuIP中的正交矩阵以及QuIP和QuaRot中的哈达玛矩阵都是随机生成的。尽管这些工作表明这些随机生成的矩阵在一定程度上可以缓解异常值问题，但它们并非最优。SpinQuant（Liu等人，2024e）发现量化网络的性能会因不同的旋转矩阵而有显著差异。例如，在MMLU基准测试中，根据所使用的旋转，下游零样本推理任务的平均准确率可能会波动高达13个点。因此，SpinQuant提出了一种基于学习的旋转变换。旋转矩阵使用凯莱随机梯度下降（Cayley SGD）方法进行学习，优化目标如下：
\(R^{}=arg min _{R \in \mathcal{M}} \mathcal{L}_{Q}(R | W, X)\)
这里，\(\mathcal{M}\)表示斯蒂费尔流形，即所有正交矩阵的集合。\(\mathcal{L}_{Q}(\cdot)\)表示任务损失。通过使用学习到的矩阵，与随机矩阵相比，性能显著提高，方差也大大减小。SpinQuant（Liu等人，2024e）中的示意图有效地展示了旋转变换的整个过程，因此我们借用它用于我们的目的，如图11所示。

我们可以观察到，缩放变换和旋转变换可用于大语言模型量化的不同部分。QServe（Lin等人，2024b）是一个为高效大语言模型服务共同设计的量化系统，它结合了缩放和旋转变换。由于在线计算旋转矩阵需要额外开销，QServe使用缩放变换代替旋转操作，从而避免了额外开销。

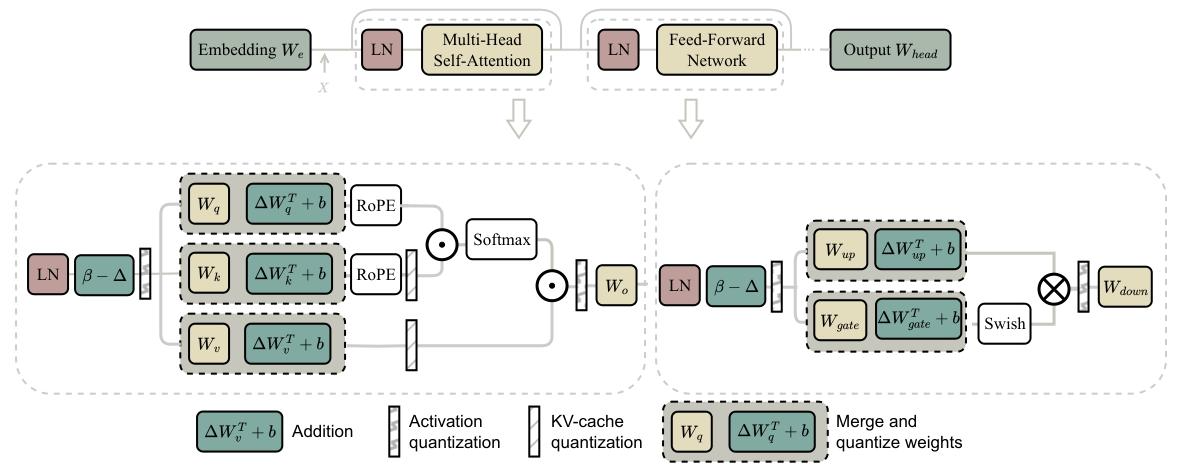
图9 移位变换整体示意图。\(\Delta\)可以合并到层归一化（LayerNorm）的参数\(\beta\)和权重矩阵中

图10 缩放变换整体示意图。\(\Phi\)可以合并到层归一化（LayerNorm）的参数\(\gamma\)和权重矩阵中

图11 旋转变换整体示意图。旋转后的激活值异常值更少，更易于量化。\(R_{1}\)和\(R_{2}\)是随机矩阵，可以合并到权重矩阵中。\(R_{3}\)和\(R_{4}\)不能合并，通常是哈达玛矩阵

 5.2.2 补偿

权重补偿技术最初源于最优脑损伤（OBD）（LeCun等人，1989），它涉及对目标函数进行泰勒级数展开。该方法假设在移除任何给定参数后，其余参数对目标函数的影响保持不变。基于OBD，OBS（Hassibi等人，1993）和OBQ（Frantar和Alistarh，2022）通过求解海森矩阵的逆来计算每个参数权重对目标函数的影响。同时，它们计算一个补偿项应用于其余权重，以抵消每次权重调整引入的误差。

尽管逐个权重量化方法在较小模型上取得了令人满意的性能，但在扩展到较大模型时，计算开销变得过高。为了加速量化，GPTQ（Frantar等人，2022）逐列对权重进行量化，并使用二阶信息补偿舍入误差。具体来说，该算法通过调整全精度权重子集\(R\)的更新\(\delta_{R}\)，来补偿量化权重\(Quant(W_{i})\)引起的量化误差：
\(W_{i}=\underset{W_{i}}{argmin} \frac{\left(Quant\left(W_{i}\right)-W_{i}\right)^{2}}{\left[H_{R}^{-1}\right]_{i i}}\)
\(\delta_{R}=-\frac{W_{i}-Quant\left(W_{i}\right)}{\left[H_{R}^{-1}\right]_{i i}} \cdot\left(H_{R}^{-1}\right)_{:, i}\)
其中海森矩阵\(H_{R}=2 X_{R} X_{R}^{\top}\)。基于GPTQ，随后提出了几项工作。QuantEase（Behdin等人，2023）利用坐标下降法为未量化的权重计算更精确的补偿。QQQ（Zhang等人，2024e）对OS +（Wei等人，2023b）转移的权重采用GPTQ方法。

 5.2.3 混合精度

如前所述，大语言模型的激活和权重中广泛存在异常值，这给量化带来了重大挑战。因此，许多大语言模型混合精度方法的动机是分别以更高精度表示少量异常值，以较低精度表示其他值。同样，根据混合精度的粒度，方法可分为元素级、通道级和张量级，如2.2节所述。
 元素级：SpQR（Dettmers等人，2023）率先证明权重中也存在异常值。它根据敏感性识别并分离这些异常值权重，将它们保存为高度稀疏的高精度矩阵。SqueezeLLM（Kim等人，2023）对非显著权重采用非均匀量化，实现了近乎无损的性能。类似地，CherryQ（Cui和Wang，2024）定义了异质性来识别关键的“樱桃”参数。为了探索极高的压缩率，PB - LLM（Shang等人，2023）首次对大语言模型中的非显著权重进行二值化。由于PB - LLM仍然为10% - 30%的显著权重分配高精度，BiLLM（Huang等人，2024）对显著权重采用残差近似，对非显著权重采用组量化，将大语言模型权重的量化比特宽度降低到1.08比特。GEAR（Kang等人，2024）将混合精度的概念扩展到KV缓存压缩，并使用低秩矩阵来近似量化残差。
 通道级：LLM.int8()（Dettmers等人，2022a）根据异常值通道将权重和激活分为两个独立部分，以最小化激活中的输出量化误差，有效地减少了推理期间的GPU内存使用。OWQ（Lee等人，2024a）提出了一种基于敏感性的混合精度方案，通过海森矩阵度量来识别弱列。此外，OWQ还提供弱列调整（WCT），以实现针对特定任务的精确参数高效微调。RPTQ（Yuan等人，2023）观察到激活中跨通道的不同范围给量化带来了挑战。因此，RPTQ将通道重新排序到不同的簇中，并分别进行量化。Atom（Zhao等人，2024）对激活采用动态重新排序，对权重采用静态重新排序，以与相应的激活通道保持对齐。Atom进一步将KV缓存量化为4比特，显著提高了服务吞吐量。受信息论的启发，CQ（Zhang等人，2024b）将多个键/值通道耦合在一起并联合量化。
 张量级：DecoQuant（Liu等人，2024b）旨在通过对局部张量进行张量分解来转移量化难度。MOE PTQ基准（Li等人，2024b）研究了不同块、专家和线性层之间的权重比特数，揭示了不同数量的权重比特是有效的。

 5.2.4 组合

尽管目前大模型的量化方法已经取得了相对较好的结果，但在极高压缩率下，由于低比特量化的表示能力有限，其性能仍然不尽如人意。目前，常用的压缩方法包括低秩分解、模型稀疏化和模型蒸馏，人们探索将它们与量化相结合。

低秩：虽然量化感知训练通常被认为能提供最佳精度，但其高昂的内存成本使其难以应用于大语言模型。因此，一些方法考虑引入LoRA或其他矩阵分解方法，作为训练后量化和量化感知训练之间的折衷方案。与3.3节中讨论的参数高效微调不同，这些方法旨在使用LoRA或SVD等技术减少量化误差，以获得更接近全精度模型的量化模型，而不是在微调数据集上增强学习能力。一些工作使用LoRA实现了参数高效的量化感知训练。LR - QAT（Bondarenko等人，2024）在正向传递中计算\(s clamp((W_{q}+A^{i ×r} B^{r ×o}))\)，在反向传递中不更新W，使得在单个具有24GB内存的消费级GPU上训练70亿参数的大语言模型成为可能。这种方法在微调后得到了一个对量化友好的模型。LLM - QFA旨在通过单个超网训练生成具有各种比特宽度的模型，利用LoRA的低资源成本显著降低了这种生成方法的资源开销。INT2.1（Chai等人，2023）利用LoRA将优化目标从最小化每层或每块的量化误差转移到最小化模型的整体输出误差。通过端到端的微调，它缩小了输出分布与其相应的原始全精度输出分布之间的差距。其他工作通过矩阵分解减少量化误差。LQER（Zhang等人，2024a）将SVD应用于量化误差，并使用激活诱导的缩放矩阵引导奇异值分布向期望的模式发展。Delta - CoMe（Ping等人，2024）发现应用SVD后，增量权重的奇异值呈现长尾分布，并提出了一种混合精度增量量化方法，对这些奇异值对应的奇异向量使用高比特表示。ZeroQuant - V2（Yao等人，2023）引入了一种优化的低秩补偿方法，通过利用量化误差的SVD得到的低秩矩阵来增强模型质量恢复。LCQ（Cai和Li，2024）使用秩大于1的低秩码本进行量化，解决了在高压缩比下使用秩一码本时的精度损失问题。

稀疏化：模型稀疏化旨在去除不重要的权重以加速模型，而量化则进一步使用低比特表示减少剩余权重。因此，这两种方法可以有效地互补使用。SDQ（Jeong等人，2024）首先根据幅度尽可能地对大语言模型的权重进行稀疏化，直到大语言模型的质量受到显著影响（例如，困惑度增加1%）。然后，它使用混合精度量化方法处理异常值。然而，这种方法没有考虑到两种方法的耦合。稀疏化和量化往往相互冲突。稀疏化倾向于保留大语言模型中绝对值较大的参数（Han等人，2015；Sun等人，2023），而量化更喜欢参数值的范围更小（Wei等人，2023b）。结果，稀疏化过程中保留的参数可能会降低量化的性能。JSQ（Guo等人，2024）设计了一种新的稀疏性度量来解决这个问题：

\(\begin{aligned} & I_{i j}=\| X\| _{2} \cdot\| W\|, \\ & A_{i j}=max \left(\hat{Y}_{: i}\right)-min \left(\hat{Y}_{: i}\right), \\ & where \hat{Y}=X \cdot(\Theta(W ; i ; j))^{\top}, \\ & S_{i j}=I_{i j}+\lambda A_{i j} . \end{aligned}\)

这里，\(\Theta(W ; i ; j)\)表示在W中将第\(i\)行和第\(j\)列的元素设置为0时的辅助权重矩阵。\(\lambda\)是一个权衡因子。通过使用这个度量，可以在保留异常值以获取更多信息和最小化激活范围以实现更好的量化之间取得更好的平衡。

量化：除了将量化与其他压缩方法相结合，不同的量化技术也可以集成以获得更好的结果。最近的一项工作（Sharify等人，2024）将SmoothQuant和GPTQ结合在一起。实际上，大多数等效变换方法和补偿量化方法是正交的，可以合并以进行进一步探索。

 5.2.5 更多量化形式

除了整数量化，更多形式的量化正在被引入大语言模型，因为它们也可以将32位或16位模型的平均比特宽度压缩到4位或更低。虽然这些方法在节省内存时并不总是能带来显著的加速优势，但它们通常会提高精度。

更多量化数据类型：整数量化通常为整个块分配一个单一的缩放因子，并将每个元素单独量化为一个整数。这减少了内存使用，并且在对权重和激活都进行量化后，还能够加速定点运算。然而，随着对大语言模型量化精度要求的提高，人们提出了更匹配原始值分布的格式。与分位数量化一起提出的Normal Float（Dettmers等人，2021，2024），是基于权重分布遵循正态分布的假设。它被认为是一种信息论上最优的数据类型，可确保每个量化区间从输入张量中分配到相等数量的值。然而，Dotzel等人（Dotzel等人，2024b）进行的统计分析发现，大多数大语言模型的权重和激活分布遵循学生t分布。基于此，他们推导出了一种新的理论上最优的格式——Student Float（SF4）。浮点（FP）量化与NF/SF相比，具有更好的硬件支持，并且比整数量化更灵活，能够更有效地处理长尾或钟形分布。由于FP可以支持指数和尾数比特的灵活分配，人们提出了几种分配方案。FPQ（Liu等人，2023a）通过联合格式和最大值搜索，并结合预移指数偏差来确定FP量化器。FP8量化（Kuzmin等人，2022）通过评估量化误差等指标测试了各种分配方案，并提出了用于可学习分配和量化的FP8量化模拟。

向量量化：向量量化（VQ）联合量化多个向量维度。它通过学习码本\(C_{1}, \ldots, C_{M}\)来实现，每个码本包含\(2^{B}\)个向量（对于B比特代码）。为了编码给定的数据库向量，VQ将其划分为条目子组，然后从学习到的码本中选择一个向量来编码每个组。第\(i\)层的部分权重通过从每个码本中选择一个代码并求和来编码：
\(\hat{W}_{i, j}=\sum_{m = 1}^{M} C_{m} d_{i j m}\)
其中\(d_{i j m} \in \mathbb{R}^{2^{B}}\)表示第\(i\)个输出单元、第\(j\)组输入维度和第\(m\)个码本的独热码。

为了表示第\(i\)层的完整权重，只需连接：
\(\hat{W}  i=\hat{W}_{1} \oplus \ldots \oplus \hat{W}_{d_{i n} / g}\)
其中\(\oplus\)表示连接。

Transformer - VQ（Lingle，2023）将向量量化（VQ）应用于注意力的键向量序列，将注意力的复杂度降低到线性。大多数其他VQ工作专注于优化码本\(C_{m} \in \mathbb{R}^{2^{B}}\)，以及由独热\(d\)表示的离散代码。AQLM（Egiazarian等人，2024b）以输入自适应的方式学习权重矩阵的加法量化，并跨每个Transformer块联合优化码本参数。QuIP（Egiazarian等人，2024b）使用向量量化来利用不相关权重中固有的球形次高斯分布，通过引入基于高度对称的E8晶格的硬件高效码本。GPTVQ（van Baalen等人，2024）将一个或多个列的量化与对其余未量化权重的更新交错进行，使用每层输出重建均方误差（MSE）的海森矩阵信息，并通过使用整数量化和基于SVD的压缩进一步压缩码本。PV - Tuning（Malinovskii等人，2024）指出使用直通估计器（STE）会导致次优结果，并提出在微调期间对尺度、码本、零点（连续参数）和分配（离散代码）进行交替迭代优化策略。QTIP（Tseng等人，2024b）使用有状态解码器将码本大小与比特率和有效维度分离，以实现超高维量化。

 5.3 量化工具包和基准测试

 5.3.1 工具包

为了对大语言模型进行量化，通常有三种基本策略：量化感知训练（QAT）、训练后量化（PTQ）和参数高效微调（PEFT）。

致力于提供全面比较的量化工具包在各个方面对流行的模型和量化算法都有很好的支持。大多数工具包包括像Llama系列、Mixtral、Vicuna等知名模型。那些更关注模型多样性的工具包，如QLLM - Eval，对各种模型有进一步的支持。在算法方面，LLMC、LMQuant和MI - optimize专注于不同量化算法的性能，并为比较提供统一、公平、全面的基准测试。所有基准测试都基于一个或几个推理框架作为后端，并为用户定义和评估任何自定义模型和算法提供接口。

 5.3.2 评估

基准测试中的评估展示了量化大语言模型最有趣的方面，即效率和生成质量。我们在表5中列出了详细的评估指标。对于效率，推理效率通过可部署性和吞吐量来衡量，这是大语言模型压缩中最关键的特征（Lin等人，2024b；Gong等人，2024）。通常，减少参数的存储理论上可以加快推理速度，但这取决于实际的系统实现。基准测试为我们提供了一个公平且方便的手段，来区分具有实际加速和存储节省效果的算法和实现。生产效率通过校准时间来衡量，它表明了训练后量化算法所需的时间和计算资源成本（Gong等人，2024）。消耗大量资源的方法通常具有更好的生成质量，而那些所需时间较少的方法可能生成性能较差。这是生产量化大语言模型时的一个权衡。对于生成质量，它有很多方面，如困惑度、准确性、逻辑性、完整性、可信度等（Lin等人，2024b；Gong等人，2024；Li等人，2024c；Liu等人，2024d）。大多数基准测试评估涌现能力，这是大语言模型的关键特征。具体来说，模型和算法在各种场景下进行测试，如对话、长上下文或多任务（Li等人，2024c）。并且一些基准测试关注生成内容的安全性，并评估大语言模型的可信度和鲁棒性（Li等人，2024c；Liu等人，2024d）。

表5 大语言模型的量化工具包和基准测试

 6 未来趋势和方向

随着大语言模型量化领域的不断发展，一些新兴趋势和研究方向有望塑造其未来。本节探讨了量化技术、模型架构和硬件设计方面的预期进展，这些进展将推动量化模型在效率、性能和应用方面的改进。
 量化技术：尽管取得了进展，但量化技术仍面临一些挑战。首先，一个主要问题是大语言模型（LLMs）中异常值的来源尚不清楚，这是进一步降低量化比特宽度的重大障碍。旨在揭示这些异常值背后内部机制的研究至关重要，将为该领域提供有价值的见解，有可能推动量化技术的发展并实现更高效的模型。其次，在可接受的精度范围内突破最小比特表示的界限非常有价值。在保持性能的同时实现尽可能低的比特宽度，可以充分利用硬件能力并最大化其潜力。第三，探索混合比特量化的统一策略，包括比特选择和层内/层间比特分配，对于优化模型性能和效率至关重要。当前方法主要强调层内混合精度，往往忽略了层间混合精度的潜在好处。最后，开发语义引导的策略以实现更低比特的量化和键值（KV）缓存的压缩将是一个主要重点。在长上下文长度的推理过程中，主要瓶颈通常在于KV缓存的大量内存使用。因此，确定有效的KV缓存压缩方法对于克服这一限制和提高模型效率至关重要。
 模型架构：模型架构的创新也将发挥关键作用。首先，将探索对处理多种模态的模型进行量化，以确保在不同数据类型和应用中的效率。其次，研究将扩展到包括对新出现的模型结构（如混合专家（MOE）和其他大规模架构）的量化策略。第三，探索量化与模型大小之间的关系，将为优化较小模型的性能同时管理量化权衡提供见解。
 硬件设计：硬件和量化协同设计的进展对于释放新的潜力至关重要。第一个重点领域是开发用于新型极低比特量化的系统。低比特表示的创新格式和高效的系统实现可能为摩尔定律带来的挑战提供新的解决方案。第二个领域涉及使用更低比特精度（如FP4）加速训练。对支持这种低比特精度训练的硬件的研究对于在保持性能的同时加快模型训练至关重要。

 7 结论

在本综述中，我们深入探讨了大语言模型（LLMs）的低比特量化技术，强调了它们在解决将这些模型部署在受限环境中时所面临的计算和内存挑战方面的重要性。我们首先阐明了低比特量化的基本原理，包括专门为大语言模型设计的新型数据格式和粒度。我们对系统和框架的回顾展示了支持不同硬件平台上低比特大语言模型的各种方法和工具。我们还对优化训练和推理的各种技术进行了分类和讨论，提供了对当前方法的全面理解。最后，我们探索了该领域的未来方向和新兴趋势，强调了潜在的研究领域和技术进步，这些可能会进一步提高大语言模型量化的效率和有效性。随着大语言模型研究领域的不断发展，本综述旨在成为推动低比特量化技术发展的宝贵资源。