前言
1. 概率与似然? 结果相同,只是视角不同。
概率是给定某一参数值,求某一结果的可能性。
例如,抛一枚匀质硬币,抛10次,6次正面向上的可能性多大?
解读:“匀质硬币”,硬币的密度参数是0.5,“抛10次,六次正面向上”这是一个结果,概率(probability)是求这一结果的可能性。
似然是给定某一结果,求某一参数值的可能性。
同理,极大似然估计就是给定一个结果,求使得结果发生可能性最大的参数
例如,抛一枚硬币,抛10次,结果是6次正面向上,其是匀质的可能性多大?
解读:“抛10次,结果是6次正面向上”,这是一个给定的结果,问“匀质”的可能性,即求参数值=0.5的可能性。
2. 最大与极大?
别激动,其实是一个东西
1.1 极大似然原理
极大似然原理其实最简单的理解就是:样本所展现的状态便是所有可能状态中出现概率最大的状态。
一个试验有若干个可能结果A1,A2,A3,…,An,若一次实验的结果是Ai发生,则自然认为Ai在所有可能结果中发生的概率最大,当总体X的未知参数θ待估时,应用这一原理,对X的样本(X1,X2,…,Xn)做一次观测实验,得到样本观察值(x1,x2,…,xn)为此一次试验结果,那么参数θ的估计值应该取为使得这一结果发生的概率为最大才合理,这就是极大似然估计法的基本思想。

1.2 均方误差的来源
我们平时使用的误差函数中均方误差无疑是回归问题中最常用的一种。但大家有没有想过,它是如何来的呢。这里便是通过极大似然估计法来确定的。
首先我们可以知道的是我们采用的特征向量x并不能包括所有的因素,即部分特征我们并没有纳入考虑。比如考虑房价的样本特征,我们不可能将卖房人的心情等等作为特征纳入输入,于是这些便成了干扰项。我们把所有的干扰项用一项ε来代替。于是我们可以得到y与x的关系式为:

这里我们将做一个概率的假设:ε为一个满足正态分布的独立随机变量,即ε~N(μ,σ^2)。
这个假设并没有严格的证明,但是根据大量的观察,我们发现大部分干扰性的随机变量符合正态分布,并且这个假设也能使得我们的拟合足够的精确,所以我们选择相信这个假设。
那么我们可以知道y与X的分布关系为
![]()
即

需要注意的是在上面的公式中,θ是固定的参数常数。现在用极大似然估计法来思考这个问题。我们已经有了一个样本空间D,那么产生这个样本空间的概率为:

这里写成关于θ的函数是因为这样方便使用极大似然估计法来思考。为了方便后续计算,取正相关的对数。

即现在我们需要使得l(θ)最大,上式我们可以发现前一项为常数,不予考虑,那么问题便转化为使得减号后面的想要最小。由于σ也是常系数我们提出来,那么剩下的问题就是调节系数θ使得

最小。
这不正是误差函数吗?然后接下来就是采用不同的优化方法使得E(θ)的值最小
是不是明白极大似然估计的原理了呢?一句话总结,就是针对一个问题,选定一个概率分布(如高斯分布,伯努利分布等等),然后求解其中的参数,如μ和σ,这变成似然方程了。哈~
也可以从贝叶斯分类来考虑,这其中也用到了极大似然估计
2.1 贝叶斯决策
首先来看贝叶斯分类,我们都知道经典的贝叶斯公式:

其中:p(w):为先验概率,表示每种类别分布的概率;
![]() :类条件概率,表示在某种类别前提下,某事发生的概率;
:类条件概率,表示在某种类别前提下,某事发生的概率;
而![]() 为后验概率,表示某事发生了,并且它属于某一类别的概率,有了这个后验概率,我们就可以对样本进行分类。
为后验概率,表示某事发生了,并且它属于某一类别的概率,有了这个后验概率,我们就可以对样本进行分类。
后验概率越大,说明某事物属于这个类别的可能性越大,我们越有理由把它归到这个类别下。
经典例子:
已知:在夏季,某公园男性穿凉鞋的概率为1/2,女性穿凉鞋的概率为2/3,并且该公园中男女比例通常为2:1,
问题:若你在公园中随机遇到一个穿凉鞋的人,请问他的性别为男性或女性的概率分别为多少?
从问题看,就是上面讲的,某事发生了,它属于某一类别的概率是多少?即后验概率p(y|x)。
设:![]()
由已知可得:

男性和女性穿凉鞋相互独立,所以![]()
(若只考虑分类问题,只需要比较后验概率的大小,的取值并不重要)。
由贝叶斯公式算出:
2.2 问题引出
但是在实际问题中并不都是这样幸运的,我们能获得的数据可能只有有限数目的样本数据,而先验概率 和类条件概率(各类的总体分布)
和类条件概率(各类的总体分布) 都是未知的。这时候,一种可行的办法就是先对先验概率和类条件概率进行估计,然后再套用贝叶斯分类器。
都是未知的。这时候,一种可行的办法就是先对先验概率和类条件概率进行估计,然后再套用贝叶斯分类器。
先验概率的估计较简单,可以直接用训练样本中各类出现的频率估计。
类条件概率的估比较困难,原因包括:概率密度函数包含了一个随机变量的全部信息;样本数据可能不多;特征向量x的维度可能很大等等。
解决的办法就是,把估计完全未知的概率密度 转化为估计参数,此时就需要用到极大似然估计。
转化为估计参数,此时就需要用到极大似然估计。
当然了,如果使用极大似然估计,概率密度函数的选取就显得很重要,结果受模型选择的影响很大,这也是它的一个缺点。
2.3 重要前提
当然,极大似然估计需要满足如下几个前提才可以发挥作用:
1.训练样本的分布能代表样本的真实分布。
2.每个样本集中的样本都是所谓独立同分布的随机变量 (iid条件),
3.有充分的训练样本。
2.4 求解极大似然函数
ML估计:求使得出现该组样本的概率最大的θ值。

实际中为了便于分析,定义了对数似然函数(不是新概念,就是取了对数后的似然函数,为了防止连乘之后数值太小造成下溢):


然后就是求上式关于θ的导数,令其为零,出去取得最大值的θ。具体实现看下面的例子。
2.5 极大似然估计的例子
例1:设样本服从正态分布 ,则似然函数为:
,则似然函数为:

它的对数:

求导,得方程组:

联合解得:

似然方程有唯一解 :,而且它一定是最大值点,这是因为当
:,而且它一定是最大值点,这是因为当 或
或 时,非负函数
时,非负函数 。于是U和
。于是U和 的极大似然估计为
的极大似然估计为 。
。
2.6 Python实现
def log_likelihood(theta, F, e):
return -.5*np.sum(np.log(2*np.pi*e**2)+(F-theta[0])**2/(e**2))借助scipy的optimize进行优化
from scipy import optimize
def neg_log_likelihood(theta, F, e):
return -log_likelihood(theta, F, e)
theta_gauss = [900, 5]
theta_est = optimize.fmin(func=neg_log_likelihood, x0=theta_gauss, args=(F, e))
总结
最大似然估计的缺点:受概率模型的影响太大。
类条件概率模型的选择显得尤为重要。如果假设的类条件概率模型正确,则通常能获得较好的结果。但如果假设模型出现偏差,将导致非常差的估计结果。
常见的是正态分布的概率密度函数
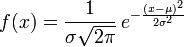
























 4630
4630

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








