LeetCode_直方图最大面积(Largest Rectangle in Histogram)

一、题目

Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

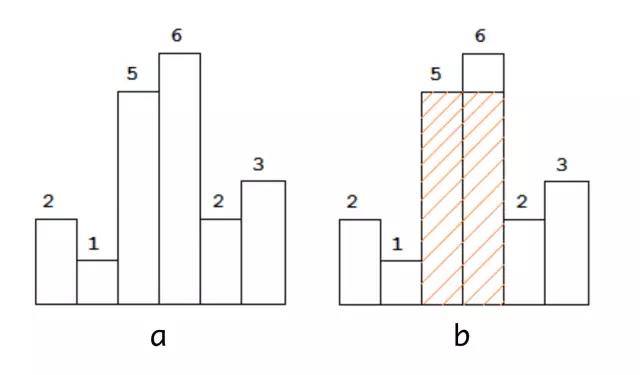
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

The largest rectangle is shown in the shaded area, which has area = 10 unit.

For example,Given height = [2,1,5,6,2,3],return 10.

LeetCode 84题：Largest Rectangle in Histogram，给定一个直方图（下图a），求直方图中能够组成的所有矩形中，面积最大为多少。对于图a来说，我们很容易看出来面积最大的矩形为高度为5和6的直方图组成的矩形（图b隐形部分），其面积为5 * 2 = 10。

---

二、解题

1.感想

如果就对于图片的示例而言，许多人一看就知道答案了，压根就不需要太多的思考，可是正是因为这种定性的思考，让我们慢慢没法“知其所以然”，也让我们慢慢失去了举一反三的思考方式，就图片的示例而言，之所以我们一看就能看出答案，是因为示例的例子数据太少了，如果数据很多的时候我们能一看就看出答案吗？所以无论面对什么样的题目，我们都不能放弃“知其所以然”，从根本解决问题。

2.暴力搜索

这道题目一个显而易见的解决方法就是暴力搜索：找出所有可能的矩形，然后求出面积最大的那个。要找出所有可能的矩形，只需要从左到右扫描每个立柱，然后以这个立柱为矩形的左边界（假设为第i个），再向右扫面，分别以（i+1, i+2, n）为右边界确定矩形的形状。

这符合我们本能的思考过程：要找出最大的一个，就先列出所有的可能，比较大小后求出最大的那个。然而不幸的是，本能的思考过程通常是简单粗暴而又低效的，就这个题目来说，时间复杂度为N^2 。

3.使用动态规划

用left[i]表示第i个柱子可以最多向左延伸至第left[i]个柱子，形成一个矩形，right[i]则表示向右延伸。遍历两次，分别计算出这两个数组。

再遍历一次，即可求出所有的柱子可以形成的最大的矩形面积。为了减少边界的判断，可以使用哨兵ÿ