Discovering Physical Concepts with Neural Networks
原文作者:Raban Iten,Tony Metger, Henrik Wilming, Lídia del Rio, and Renato Renner
翻译者:Wendy
S1 资源和方法( Materials and Methods)
这项工作中使用的神经网络的输入是观察数据和问题,输出大小是潜在神经元的个数,编码器和解码器的大小。假设编码器和解码器足够大,不会限制网络的表达能力,(并且足够小,可以有效训练),那么编码器和解码器中潜在神经元的数量对于结果并不重要。模型的训练由训练样本的数量,批量大小,训练的步骤,学习率和参数β的值确定(第S4部分会详细讲解)。为了测试网络的效果,我们使用了训练时未使用的数据,对于表S1和S2的结果(在S5中会有详细的介绍)中给出的实例。我们在这里只是给出参考值。
源代码,以及与网络结构有关的细节和训练过程,以及经过预训练的SciNet网络可以在以下链接中获取:
https://github.com/eth-nn-physics/nn physical concepts.
这些网络模型都是用tensorflow实现的,对于所有的示例,在一台标准笔记本电脑上,训练过程仅仅需花费几个小时。


S2 与先前工作的详细比较(Detailed comparison with previous work)
神经网络已经成为解决问题的标准工具,在这些问题中,我们希望不遵循特定算法或不对可用数据施加结构的情况下进行预测,并且它们已被广泛应用于物理问题。例如,在凝聚态物理学中以及通常在多体环境中,神经网络已被证明对表征相变和学习局部对成性特别有用。
在量子光学中,基于自动搜索技术和强化学习技术的方案已用于生成新的实验装置。参考文献[9]中使用投影仿真来自主发现具有最大通用性的实验构建块。
与我们实验有关的,神经网络已经用于有效地表示特定量子系统的波函数。特别地在参考文献[12]中,变分自动编码器用于固定测量基础上近似特定量子态测量结果的分布,并且神经网络的大小可以提供状态复杂性的估计。相反,我们的方法不再仅仅关注对于一个给定量子状态的有效表示,它不是为了特定的量子系统而设计的。尽管如此,SciNet可以用于生成简单量子系统的任意态的表示而无需重新训练网络模型。这就可以使我们能够提取有关表示(小)量子系统任何状态所需的自由度的信息。
文献[26]提出了另一种以无监督的方式提取物理知识的方法。作者展示了在假设输入来自Boltzmann分布的假设下如何提取经典统计力学中系统的相关自由度。他们用信息论来指导受限玻尔兹曼机(一种概率神经网络)的无监督训练,以近似概率分布。
不同的工作重点是使用神经网络和其他算法技术来更好地理解人类如何获得对物理学的直观解释。
最近,从动态系统的时间序列数据中以无监督方式提取了物理变量。参考文献[37]中的网络结构建立在交互网络[38,39,40]上,非常适合由以称对方式交互的几个对象组成的物理系统。网络结构中包含的先验知识使网络可以概括为与训练期间所见情况大不相同的情况。
在过去的几年中,有意义的进展是从数据中获取动力学方程,这个问题被成为NP难题。这些工作大部分都在输入数据中搜索动力学方程模型,在参考文献[43,44,45]中神经网络中使用了新的变量集,以使新变量的演化近似线性(受Koopman 理论的推动)。在S4,5节中给出的实例中使用与[43,44,45]中使用的网络结构类似,这对应于SciNet的一种特殊情况,它具有繁琐的问题的输入和随时间变化的潜在表示。在这个潜在表示中发展系统的概念已经用于机器学习中,如从视频数据中提取相关特征。
参考文献[52]向人工智能物理学家迈进了一步,其中来自复杂环境的数据被自动分成与系统相对应的部分,其中来自环境的复杂数据被自动分成与系统相对应的部分,这些部分可以用简单的物理定律来解释。然后,机器学习系统尝试统一为数据的不同部分找到它的基础“理论”。
S3 最小化表示(Minimal representations)
在这里,我们描述了设计SciNet并帮助其查找编码物理原理的有用表示形式时需要用到的一些理论基础。给定数据集,找到包含所有所需信息的数据的简单表示通常时一件复杂的事情。 SciNet应自行恢复此类表示;但是,我们鼓励它在训练期间学习简单的表示形式。为此,我们必须指定所需表示的所需属性。在这种情况下,我们的方法遵循了关于表征学习理论的几篇著作的思想[53,54,55,56,57,58]。
为了进行理论分析,我们在数据上引入了一些其他结构,这些结构时表述所需表示形式所需的。我们考虑实值数据,我们认为该数据时从一些未知的概率分布中采样的。即,我们将随机变量分配给观察值O,问题Q,潜在表示R和答案A。我们使用约定,随机变量X=(X1,X2,…,X|X|),表示样本X∈R|X|,其中|X|表示空间的维度。特别地,|R|将会符合潜在表示神经元的个数。
对于三元组(O,Q,a_corr)所描述的数据,我们需要以下属性来表示不相关(足够)的表示R(由编码器映射E:O→R定义),其中函数a_corr表示为O×Q→A,输入观察值o∈O和问题q∈Q得到的答案a∈A和实际答案之间的差值。
- 充足(平滑的解码器):存在一个平滑的映射D:R×Q→A,如D(E(o),q)=a_corr(o,q),对于所有可能的观察值o∈O和q∈Q。
- 不相关的:代表元素集合{R1,R2,…R|R|}都是相互独立的。
属性1:假设编码器映射E对观察值 o ∈ O的所有信息进行编码,这些信息对于回答所有可能的问题q ∈Q是必须的。我们要求解码器是平滑的,因为这使我们能够给潜在表示中存储的参数数量赋予一个明确定义的维度含义。(请参阅S3.1节)
属性2:意味着了解潜在表示中的某些变量不会提供有关任何其他潜在变量的任何信息;请注意,这取决于观察值的概率分布。
我们将最小不相关表示R定义为具有最少参数|R|的不相关(足够)表示。这使我们认为是物理数据的“简单”表示形式正式化。
如果不假设解码器是平滑的,则从理论上讲,只有一个潜在变量就足够了,因为实数可以存储无限量的信息。因此,标准信息论中的方法(如信息瓶颈[59,60,61])并不是正确的变量数量形式化工具。在 S3.1节中,我们使用微分几何中的方法来证明变量数量为|R|。最小(足够)的表示形式对应于回答所有可能问题所需的观测数据中相关自由度数量。
S3.1 解释潜在变量的数量(Interpretation of the number of latent variables)
以上,我们要求潜在表示应该包含最少数量的潜在变量;我们现在将此数字与给定数据的结构相关联。根据命题2的定义,潜在神经元的最小数量对应于回答所有可能提出问题所需的观测数据中的相关自由度。
为了简单起见,我们在这里用集合而不是随机变量来描述数据。注意,概率结构仅在第S3节中用于属性2,在这里,我们仅对潜在神经元的数量感兴趣,而不是它们相互独立。因此,我们考虑三元组(O,Q,a_corr),其中O和Q是包含观察值数据和问题的集合,函数a_corr:(o,q)→a发送一个观察值o ∈O和一个问题q ∈Q去正确回答问题a ∈A。
直观地,我们认为三元组(O,Q,a_corr)至少有n维,假如Q中存在问题可以从观察值中捕获n个自由度。从某种意义上说,这种要求的平滑性是自然的要求,因为我们希望在小的扰动下,答案对输入的依赖性会很强。正式定义如下:
定义1(数据集的维度):考虑由三元组描述的数据集(O,Q,a_corr)其中,a_corr:O×Q→A,所有集合都是由实值组成,
我们说如果存在n维子流形,则该三元组的维数至少为n,O_n ⊆ O ,问题q1,…,qk ∈Q由此存在函数
像 f : On → f(On) 一样是一个变分函数。
推论2:(SciNet的最小表示)对于由至少三倍维数数据(足够)的潜在表示,至少需要n个潜在变量。
证明:通过假设,存在一个n维的子流形O_n ⊂O,k个问题q1,…,qk ,像f : On →In := f(On)是一个可谓同构函数。我们通过反正这个定义:假设存在一个由编码器描述的(足够)表示E : O → Rm ⊂ Rm其中m < n 潜在变量。通过表示的充分性,存在一个光滑的解码器D : Rm ×Q → A像D(E(o),q) = a_corr(o,q) 对于所有的观察值 o ∈O和问题q ∈Q,我们可以定义一个光滑的映射:
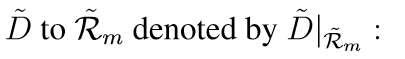
是一个光滑的映射。但是根据Sard定理(参见[62]),图](https://i-blog.csdnimg.cn/blog_migrate/d8f217e76b8f5eea5f7879979f0ffb3f.png)
我们可以将自动编码器视为SciNet的特例,我们总是提出相同的问题,并期望网络重现观察输入值。因此,一个自动编码器可以由一个三元组(O,Q = {0},a_corr : (o,0) → o)来描述。作为命题2的推论,我们表明,在自动编码器的情况下,所需的潜在变量数与描述观察输入的“相关”自由度数相对应。相关自由度在表示学习这种情况下称为(潜在隐藏)生成因子(参见[57]),可以用光滑的非退化数据生成函数H的域维来描述,定义如下:
定义3:如果存在一个开放子集N_d ⊂G,使得函数H对N_d 的限制H|_N_d : N_d → H(N_d) 是微分同构的,则光滑函数H : G ⊂ Rd → Rr 是非退化的。
可能会想到H是在高维观测空间中将数据的一维表示发送到流形上。
推论4(自动编码器的最小表示):
证明:


S4 神经网络(Neural networks)
关于神经网络和深度学习,详细的讲解请见参考文献[3],这里仅仅给出一个很简短的介绍。

单个神经元(Single artificial neuron) 神经网络的构建块是单个神经元(如图S1a所示)。我们认为一个神经元由多个实值输入x1,…,xn 和一个经过激活函数之后的输出,

其中权重 wi ∈ R和偏差 b ∈ R 都是可调参数。一个神经元的输出本身有时会用激活值来表示,并且有多种不同的激活函数可以选择。为了实现本文的实例,我们使用指数线性激活函数(ELU) ,(如图S1b所示),将参数α > 0的ELU函数定义为
神经网络(Neural network) 通过将神经元分层排列并将第i层神经元的结果作为第(i+1)层神经元的输入,来构建(前馈)神经网络(参见图S1c)。整个神经网络可以看作函数F : Rn → Rm,其中 x1,…,xn 对应于第一层(输入层)中神经元的激活。输入层的激活值形成第二层的输入值,第二层是隐藏层(神经网络中除了输入层和输出层,其他均称为隐藏层)。在完全连接网络的情况下,第(i+1)层中的每个神经元都将第i层中所有神经元的激活值作为输入。最后一层中的m个神经元的激活被称为输出层,然后被解释为函数F的输出。可以证明,神经网络是通用的,在某种意义上说,任何连续功能都可以通过使用足够多的隐藏层神经元而被一个仅有一个隐藏层的前馈神经网络很好的近似模拟。有关结果的数学说明,请参见[64,65],可视化在[3]中给出。
训练(Training) 神经网络中的权重和偏差参数不是通过手动调整的,而是通过训练样本优化的,已知输入——输出(x,F*(x)),我们想尽可能的近似F*(x)。我们可以将神经网络视为一类由θ参数化的函数{Fθ}_θ,其中包含网络中所有神经元的权重和偏差参数。一个损失函数 C (x,θ) 用来测量对于输入x,网络的输出F_θ(x) 和期望的输出F*_θ(x)之间的差值。例如,最常用的一个损失函数是
一个网络的权重和偏差的初始化都是随机的。通过梯度下降算法来更新参数θ。通过对损失函数求对所有输入x的梯度下降方向改进。实际上,所有训练样本上的梯度平均值通常被较小样本的训练样本上的平均值(称为最小批量)所替代。然后,该算法称为随机梯度下降。反向传播算法用于有效地执行梯度下降步骤(详细信息见参考文献[3])。
S4.1 变分自动编码器(Variational auto-encoders)
SciNet 的实现使用了所谓的变分自动编码器(VAE)的改进版本。标准的VAE体系结构不包括SciNet 使用的问题输入,而是尝试从表示形式中重建输入,而不仅仅是回答问题。VAEs 是表示学习领域中使用的一种特定体系结构。在这里,我们详细介绍了表征学习的目标和VAEs 的详细信息。
表示学习(Representation learning) 表示学习的目标是将高维输入向量x映射到低维表示 = (z1,z2,…,zd),通常称为潜在向量。表示形式z仍应包含有关x的所有相关信息。对于自动编码器,z表示重建后的X。这是由(低维)表示越好,可以从中恢复原始数据越完整这个想法所激发的。具体来说,自动编码器使用神经网络(编码器)将输入x映射到一个小数平坦的神经元。然后,另一个神经网络(解码器)用于重建输入的估计值,即z→x~ 。在训练过程中,对编码器和解码器进行优化,以最大程度地提高重建精度,并达到x=x~。
概率编码器和解码器(Probabilistic encoder and decoder) 代替考虑确定性映射x→z和z→x~,我们用编码器和解码器的条件概率分布p(z|x) 和p( x˜|z)泛化。这是由贝叶斯(Bayesian )思想所激发的,即编码器可以提供最优信息量的陈述,可以输出所有潜在矢量的概率分布的描述而不是输出单个估计。解码器具有相同的推理。我们使用记号 z ∼ p(z)表示根据分布 p(z)随机选择 z。
我们不能通过分析数据来表示一般的情况,所以我们做一个限制性的假设来简化设置。首先,我们假设输入可以通过神经网络的编码器和解码器进行完美的压缩和重建,即假想理想分布 p(z|x)和p( x˜|z)可以达到x=x˜都可以被参数族{pφ(z|x)}φ和{pθ(x˜ |z)}θ记住。我们进一步假设,通过每个神经元彼此独立的潜在表示可以实现这一目标pφ(z|x) =Π_i pφ(z_i|x)。如果对于给定的潜在表示维数d很难发现这些分布,我们可以尝试增加表示的神经元数量以解开它们。最后,我们做一个简单的假设,该假设可以通过良好的结果来证明是后验的:我们可以通过仅对每个潜在神经元使用独立正态分布来达到p(z|x) 的良好近似, pφ(zi|x) = N(µi,σi), 其中 µi是均值, σi是方差。我们可以认为编码器将x映射到向量 µ = (µ1,…,µd)和σ = (σ1,…,σd)。然后按照如下方法学习φ和θ 的最佳值:
- 参数(权重和偏差)为φ的编码器将输入x映射到pφ(z|x) = N[(µ1,…,µd),(σ1,…,σd)];
- 从pφ(z|x)中得到潜在表示z;
- 具有参数(权重和偏差)为θ 的解码器将潜在矢量z映射到 pθ( x˜|z);
- 更新参数φ和θ 以在解码器分布pθ( x˜|z)下最大化原始输入x的可能性。
更新参数的技巧(Reparameterization trick) 从pφ(z|x)中采样获得潜在矢量z的操作相对于网络的参数φ和θ是不可区分的。然而,使用随机梯度下降训练网络是必须的,通过参考文献[53]中引入了的重新参数化技巧解决了这个问题:如果 pφ(zi|x) 是一个均值为 µi标准差为σi的高斯分布,我们可以使用辅助随机数代替采样操作εi ∼ N(0,1)。然后可以通过zi = µi +σiεi来生成潜在变量zi ∼ N(µi,σi) 。采样 εi 不会干扰梯度下降,因为 εi 独立于训练参数φ和θ。或者,可以将这种采样方式视为将噪声注入到潜在层。
β-VAE成本函数(β-VAE cost function) 在参考文献[53]中导出了用于优化参数φ和θ的易计算的成本函数。在参考文献[57]中扩展了此成本函数,以鼓励在潜在变量z1,…,zd的独立性,参考文献[57]中的成本函数即为β-VAE成本函数。
其中h(z) 是潜在变量z的先验分布,通常是单位高斯分布,β ≥ 0是常数,DKL是 Kullback-Leibler (KL)散度,表示概率之间的准距离度量分布,
让我们对β-VAE成本函数背后的原理做一个直观的解释。第一项是对数似然因子,它鼓励网络高精度重建输入数据。它表示“对于每个z,解码后我们恢复为原始输入x的可能性有多大?”并从pφ(z|x)采样到的z上取似然对数 pθ(x|z) 的期望值(这里可以用使用其他品质因数代替对数),以模拟编码。实际上,这种期望通常是用一个样本来估计的,如果选择的小批次足够大,效果会很好。
第二项是鼓励解码器重建表示,用KL散度的标准属性来度量。我们的目标是最小化潜在表示zi与输入值x,因此,我们可以通过最小化他们之间的KL散度DKL [p(z)||Πi p(zi)] 来实现。对于其他带有独立zi的分布h(z) =Πi h(zi),这个KL散度满足:
KL散度进一步与其突出的论点相结合,意味着
结合以上的式子,我们可以得到
右边的项恰好对应于成本函数的第二项,因为在训练中我们尝试使 Ex∼p(x) Cβ(x)最小化。选择较大的参数β也会影响潜在表示z的大小,从而激励网络学习有效的表示。有关大β效应的实证检验,参见参考文献[57];有关使用信息瓶颈方法的另一理论论证,参见[58]。
为了简单表示Cβ,我们进一步假设pφ(z|x) = N(µ,σ)。此外,我们假设解码器的输出 pθ(x˜ |z)是具有均值x^和固定协方差矩阵σ ^= 1 √2的多元高斯分布。在这些假设下,β-VAE成本函数可以被写成:
常数项C不会对用于训练的梯度有所贡献,因此可以忽略。(常数的导数为0)
S5 有关物理实验的详细信息( Details about the physical examples)
接下来,我们将提供有关我们应用了SciNet的四个简单物理系统实例的更多信息,这些实例在正文中已被简单提到。
S5.1 阻尼摆( Damped pendulum)
我们首先考虑经典物理中的一个简单实验——阻尼摆。详细描述如方框S1所示。时间演化系统用一个可微分的方程表示−κx−b x’ = mx’’, 其中k是弹簧常数,决定振荡的频率,b是阻尼因子,保持质量m不变(它是比例系数,可以通过定义k’= κ/m ,b’= b/m),因此k和b是唯一可变的参数。我们在这里考虑弱阻尼的情况,在方框S1中给出了运动方程的解。
我们选择一个具有3个隐藏神经元的SciNet网络结构。作为输入,我们提供了摆锤关于位置的时间序列,并要求SciNet预测将来某一时间的位置(有关详细信息请参见框S1)。训练后由SciNet给出的预测的准确性如图S3a所示。
在没有给与任何物理概念的情况下,SciNet会从(模拟的)时间序列数据中提取出摆锤x坐标的两个相关的物理参数,并存储最小的潜在表示。如图S3b所示,第一个神经元几乎线性的依赖于b,并且几乎独立于k,而第二个潜在神经元仅线性的依赖于k。因此,SciNet恢复了物理学家使用的与时间无关的参数k。第三个潜在神经元几乎是恒定的,并且不提供任何其他信息,换句话说,SciNet认识到两个参数足以对这种情况进行编码。


S5.2 角动量守恒( Conservation of angular momentum)
物理学中最重要的概念之一是守恒定律,例如能量守恒和角动量守恒。尽管它们与对成性的关系使它们本身对物理学家来说很有趣,但守恒定律对实际也很重要。如果两个系统复杂的相互作用,我们可以使用守恒定律从另一个系统的行为中判断一个系统行为,而无需研究它们之间相互作用的细节。因此对于某些类型的问题,守恒量充当多个系统联合特性的压缩表示。
我们考虑图S4中所示和方框S2中描述的散射实验,其中两个点状粒子碰撞。给定两个粒子的初始角动量和其中一个的最终轨迹,物理学家可以使用总角动量守恒来预测另一个粒子的轨迹。
为了了解SciNet是否以与物理学家相同的方式利用角动量守恒,我们用框S2中描述的(模拟的)实验数据对它进行训练,其中包含一个隐藏神经元,并加上高斯噪声以表明编码和解码器的稳定性。SciNet确实完成了物理学家的工作,并将总角动量存储在潜在表示中(图S4b)。这个例子表明,SciNet可以恢复守恒定律,并建议通过压缩数据并询问有关多个系统联合特性的问题自然而然地出现。


S5.3 量子位表示( Representation of qubits)
量子状态层析成像是一个很热门的研究领域。理想情况下,我们寻找一个稳定可信的量子系统状态表示形式,例如波函数:一种表示形式,该表示形式存储了所有必要信息,以预测该系统上任意测量结果的概率。但是,要指定一个可信的量子系统表示,就不必对系统进行所有理论上可能的测量。 如果一组测量足以重建完整的量子态,则将这组称为断层扫描。
在这里,我们表明,仅基于(模拟)实验数据,而没有给出任何关于量子理论的假设,SciNet可以很好地再现小量子系统的状态并可以做出准确的预测。 尤其是,这使我们能够推断系统的大小,并从断层摄影中将不完整的测量集区分出来。 方框S3总结了设置和结果。
n个量子位上的(纯)状态可由归一化复矢量ψ ∈ C2n, 表示。其中,当且仅当两个状态ψ和ψ’相差一个全局相位因子时,即存在φ∈R使得ψ=e^ iφ ψ’时,才能确定这两个状态。全局相位因子的归一化条件和不相关性将量子态的自由参数数量减少了两个。由于复数有两个实参数,单量子位状态由2×2^1 -2= 2描述真实参数,和两个量子比特的状态由2×2 ^2 -2= 6描述真实参数。
在这里,我们考虑n个量子位二进制投影测量。就像状态一样,这些测量可以用向量ω∈C2n描述,测量结果用0表示ω上的投影,否则用1表示。然后,在状态ψ上的量子系统上测量ω时得到结果0的概率为 p(ω,ψ) = |<ω,ψ>| ^2,其中<·,·>表示C2n上的标准标量积。
为了生成SciNet的训练数据,假设我们在实验室中有一个或两个量子位,可以在任意状态下进行准备,并且能够在集合M中执行二进制投影测量。我们随机选择n1个测量值M1:= {α1,…,αn1}⊂M,我们由此来确定量子系统的状态。我们在同一个量子态ψ上多次执行M1中的所有测量,以估计第i次测量的测量值为0的概率p(αi,ψ)。 这些概率构成了对SciNet的观察输入。
为了参数化度量ω(其结果概率应由SciNet预测),我们选择另一组随机度量M2 := {β1,…,βn2} ⊂ M。概率p(βi,ω)作为给SciNet的问题输入。我们总是假设我们在M2中选择了足够的测量值,以便它们可以区分所有可能的测量值ω∈M,即,我们假设M2在层析成像上是完整的。然后,SciNet必须预测用于测量M2的概率p(ω,ψ)。 当执行测量ω时,状态ψ的结果为0。
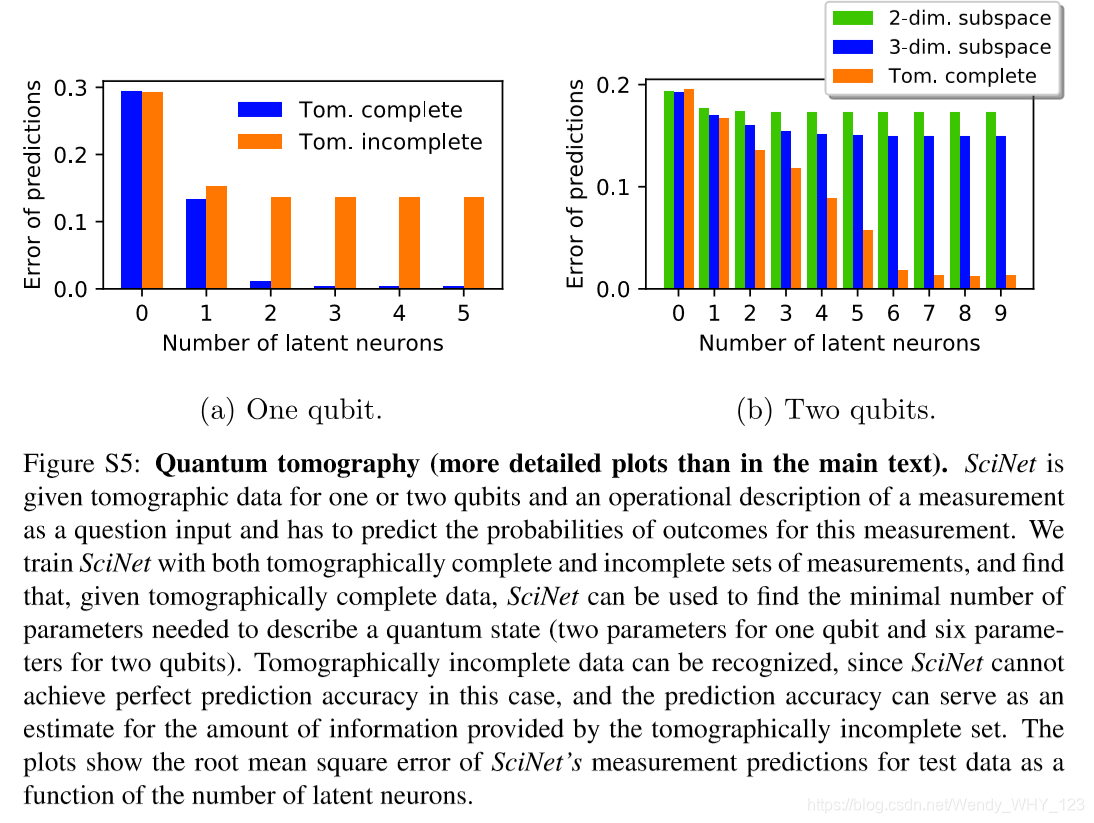
我们针对一个和两个量子位用不同对(ω,ψ)训练SciNet,并保持测量集M1和M2固定。 对于单量子位情况,我们选择n1 = n2 = 10,而对于双量子位情况,我们选择n1 = n2 = 30。 结果显示在图S5中。
改变潜伏神经元的数量,我们可以观察到预测质量如何提高,因为我们允许在ψ表示中使用更多参数。 为了使由于网络随机初始化而引起的统计波动最小化,每个网络规范都要进行3次训练,并使用测试数据上均方差预测误差最低的运行。
对于要在成像上完成M1的情况,图S5中的图显示了当潜伏神经元的数量分别由两个到六个时,一个或两个量子位的情况,预测误差的下降。这与参数的数量一致 需要描述一个或两个量子位的状态。 因此,SciNet允许我们从断层成像的完整测量数据中提取基础量子系统的维数,而无需任何有关量子力学的先验信息。
SciNet还可以用于确定测量集M1在断层成像方面是否完整。 为了生成图像上不完整的数据,我们从所有二进制投影测量的子集中随机选择M1中的测量。 具体而言,与M1中的测量相对应的量子态被限制为k个正交态的随机实线性叠加,即(实)k维子空间。 对于单个量子位,我们使用二维子空间。 对于两个量子位问题,我们同时考虑了二维和三维子空间。
在关于状态ψ的断层图像不完整数据情况下,不管潜伏神经元的数量如何,SciNet不可能完美地预测最终测量结果(见图S5)。因此,我们可以从SciNet的输出中推断出M1是一组不完整的测量值。此外,该分析为断层扫描不完全测量提供的信息量提供了定性度量:在两个量子位的情况下,将子空间维数从两个增加到三个会导致更高的预测精度,并且所需的潜伏神经元数量也会增加。

S5.4 太阳系的日心模型( Heliocentric model of the solar system)
正文中已经给出了有关该示例的所有详细信息,并在方框S4中进行了总结。

S6 循环参数的表示(Representations of cyclic parameters)
在这里,我们解释了学习循环参数表示的神经网络的困难,这在量子位示例的上下文中被提及(有关计算机视觉的详细讨论,请参见S5.3节,[67,68])。 通常,如果我们要表示的数据O形成一个封闭的流形(即无边界的紧凑流形),例如一个圆,一个球体或一个Klein瓶,就会出现此问题。 在这种情况下,需要多个坐标图来描述该流形。
例如,让我们考虑位于单位球面O上的数据点O = {(x,y,z) : x² + y² + z²= 1}, 我们希望将其编码为一个简单的表示形式。可以使用球坐标φ∈[0,2π)和θ∈[0,π](全局)对数据进行参数化,其中(x,y,z)= f(θ,φ):=(sinθcosφ,sinθsinφ,cosθ)。我们希望编码器执行映射f-1,其中为简单起见,定义f-1((0,0,1))=(0,0)和f-1((0,0,-1))=( π,0)。对于θ∈(0,π),此映射在球体上φ= 0的点上不连续。因此,使用神经网络作为编码器会导致问题,因为此处介绍的神经网络只能实现连续功能。在实践中,网络被迫以平均陡峭的连续功能逼近编码器中的不连续性,这导致接近不连续性的点产生高误差。
在量子示例中,出现了相同的问题。为了用两个参数对一个量子比特状态ψ进行参数化,可以使用具有θ∈[0,π]和φ∈[0,2π)的布洛赫球:状态ψ可以写成ψ(θ,φ)=(cos(θ/ 2), eiφsin(θ/ 2))(详细内容请参阅[69] )。理想情况下,编码器将执行E : o(ψ(θ,φ)) := (|hα1,ψ(θ,φ)i|2,…,|hαN1,ψ(θ,φ)i|2) → (θ,φ) 对于固定二元投影测量值αi∈C2,但是,这样的编码不是连续的。 实际上,假设编码器是连续的,则会导致以下矛盾:
我们在第二个等式中使用了φ的周期性,以及Bloch球面表示和标量积(因而是o(ψ(θ,φ)))以及编码器(假设)在φ中是连续的事实 在第三个平等。




























 1166
1166

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








