2 Denoising Diffusion Probabilistic Model (DDPM)
目录
2 Denoising Diffusion Probabilistic Model (DDPM)
2.2 The magical scalars √αt and 1 − αt
2.5 Rewrite the Consistency Term
2.6 Derivation of q_φ(x_t−1|x_t, x_0)
2.9 Inversion by Direct Denoising (InDI)
在本节中,我们将讨论Ho等人[4]的DDPM。如果您在网上被数千个教程混淆,请确保 DDPM 不复杂。您需要了解的所有内容都是以下摘要:
扩散模型是增量更新,其中整体的组装为我们提供了编码器-解码器结构。从一种状态到另一个状态的转换是通过降噪器实现的。
为什么增加。就像把巨船的方向转向一样。你需要慢慢地将船转向你想要的方向,否则你就会失去控制。同样的原则也适用于你的生活、你的公司人力资源、你的大学管理、你的配偶、你的孩子和你的生活周围的任何东西。“一次结束一次英寸!”(Credit:Sergio Goma,他们在电子成像 2023 年发表该评论。)
扩散模型的结构如下所示。它被称为变分扩散模型[5]。变分扩散模型具有一系列状态 x0, x1, ..., xT:·
- x0:它是原始图像,与 VAE 中的 x 相同。
- xT :它是潜在变量,与 VAE 中的 z 相同。由于我们都是惰性的,我们希望 xT ∼ N (0, I)。
- x1, ..., xT -1:它们是中间状态。它们也是潜在变量,但它们不是白高斯的。
变分扩散模型的结构如图7所示。正向和反向路径类似于单步变分自编码器的路径。不同之处在于编码器和解码器具有相同的输入输出维度。所有前向构建块的组装将为我们提供编码器,所有反向构建块的组装将为我们提供解码器。

图 7:变分扩散模型。在该模型中,输入图像为x0,白噪声为xT。中间变量(或状态)x1,。, xT -1 是潜在变量。从 x_t-1 到 x_t 的转换类似于 VAE 中的前向步骤(编码器),而从 x_t 到 x_t-1 的转换类似于 VAE 中的反向步骤(解码器)。然而,请注意,这里的编码器/解码器的输入维度和输出维度是相同的。
2.1 Building Blocks
过渡块 第t个过渡块由三个状态x_t−1,x_t和x_t+1组成。得到状态x_t有两种可能的路径,如图8所示。
- 从x_t−1到x_t的正向过渡。相关的转换分布是 p(x_t|x_t−1)。简而言之,如果您告诉我们 x_t-1,我们可以根据 p(x_t|x_t-1) 告诉您 x_t。然而,就像 VAE 一样,转换分布 p(x_t|x_t−1) 永远不会访问。但是这没事。像我们这样的懒惰的人只会用高斯q_φ(x_t|x_t−1)来近似它。我们将稍后讨论确切的形式 q_φ,但它只是一些高斯。
- 反向转换从 x_t+1 到 x_t。同样,我们永远不知道 p(x_t|x_t+1),但这是好的。我们只使用另一个高斯 p_θ (x_t|x_t+1) 来近似真实分布,但它的平均值需要由神经网络估计。
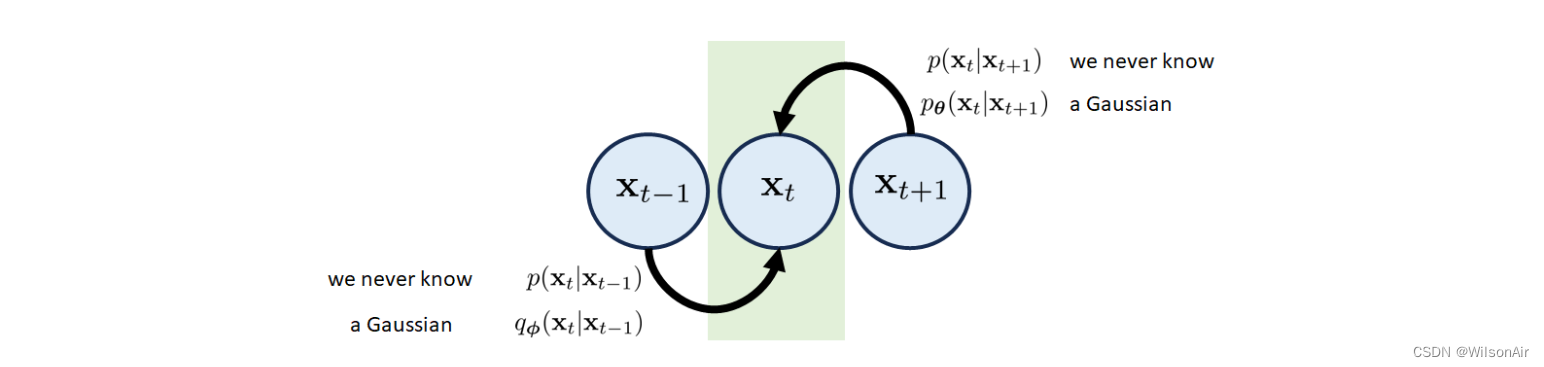
图 8:变分扩散模型的转换块由三个节点组成。过渡分布 p(xt|xt+1) 和 p(xt|xt−1) 无法访问,但我们可以通过高斯来近似它们。
初始块. 变分扩散模型的初始块集中在状态x_0上。由于我们研究的所有问题都是从x_0开始的,所以只有从x_1到x_0的反向转换,也没有从x−1到x0的反向转换。因此,我们只需要担心p(x_0|x_1)。但是由于我们可能永远不会知道 p(x_0|x_1) 的真实分布,我们通过高斯 p_θ (x_0|x_1) 来近似它,其中平均值是通过神经网络计算的。有关说明,请参见图 9。

图 9:变分扩散模型的初始块侧重于节点 x0。由于在时间 t = 0 之前没有状态,我们只从 x1 到 x0 有反向转换。
最终块. 最后一个块专注于状态 x_T。请记住 x_T 应该是我们最终的潜在变量,它是一个高斯白噪声向量。因为它是最后一个块,只有从 x_T-1 到 x_T 的前向转换,并且没有像 x_T+1 到 x_T 那样。正向跃迁近似为q_φ(x_T |x_T−1),即高斯。有关说明,请参见图 10。

图 10:变分扩散模型的最终块集中在节点 xT 上。由于时间 t = T 后没有状态,我们只有一个从 x_T -1 到 x_T 的前向转换。
了解过渡分布。在我们进一步继续之前,我们需要稍微绕道一下过渡分布 q_φ(x_t|x_t−1)。我们知道它是高斯的。但是我们仍然需要知道它的正式定义,以及这个定义的起源。
过渡分布 q_φ(x_t|x_t−1)。在去噪扩散概率模型中,过渡分布q_φ(x_t|x_t−1)定义为:
换句话说,均值为,方差为1−α_t。比例因子 √α_t 的选择是确保方差幅度被保留,以便在多次迭代后不会爆炸和消失。
例。让我们考虑高斯混合模型
给定转移概率,我们知道
对于混合模型,很难表明 x_t 的概率分布可以通过 t = 1, 2, ..., T 的算法递归计算:
其中 μ_{1,t−1} 是 t-1 处的平均值,μ_{1,0} = μ_1 是初始平均值。类似地,σ^2 _{1,t−1} 是 t-1 处的方差,σ^2_{1,0} = σ^2_1 是初始方差。
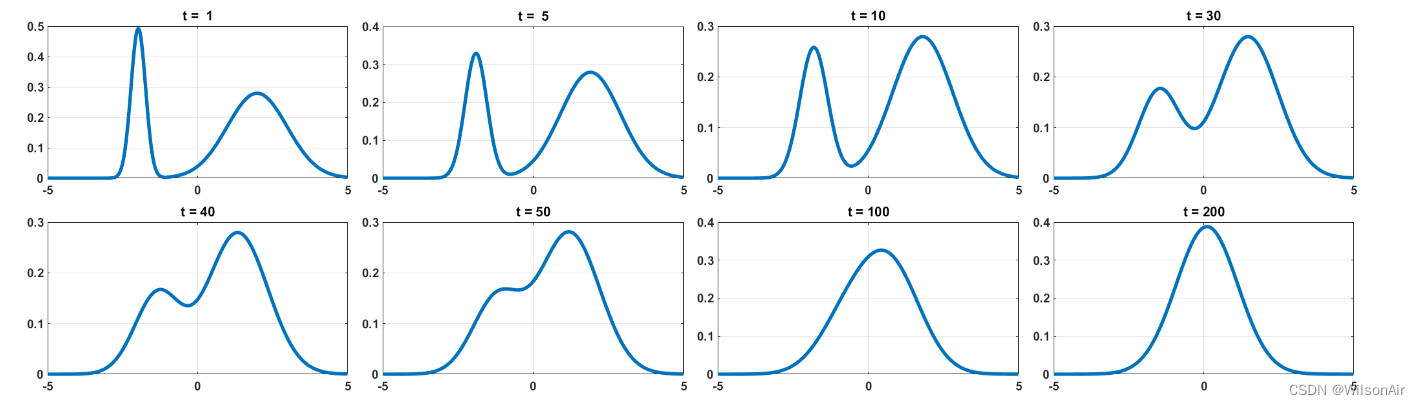
在下面的图中,我们展示了 π_1 = 0.3、π_2 = 0.7、μ_1 = -2、μ_2 = 2、σ_1 = 0.2 和 σ_2 = 1 的示例。对于所有 t,速率定义为 α_t = 0.97。我们绘制不同 t 的概率分布函数。
(随着时间t增大,p_t(x)趋向于标准的正态分布. wilson)
备注。对于那些想理解我们如何推导方程(16)中混合模型的概率密度的人,我们可以展示一个简单的推导。考虑一个混合模型
如果我们考虑一个新变量
其中 ε ∼ N (0, I),则 y 的分布可以通过使用总概率定律推导出来:
由于 y|k 是高斯随机变量 x 和另一个高斯随机变量 ε 的线性组合,并且 y 将保持为高斯。平均值是
因此,
。这完成了推导。
2.2 The magical scalars √αt and 1 − αt
你可能想知道,对于上述转移概率,genie(去噪扩散的作者)如何提出魔法标量√αt 和 (1 − αt)。为了揭开这一点,让我们从两个不相关的标量 a ∈ R 和 b ∈ R 开始,我们将转换分布定义为
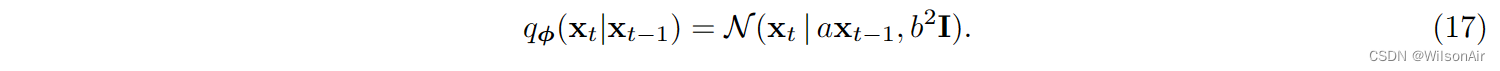
这是经验法则:
为什么 √αt 和 1 - αt?
我们希望选择 a 和 b 使得当 t 足够大时,x_t 的分布将变为 N (0, I)。事实证明答案是 a = √α 和 b = √1−α。
证明。我们想证明 a = √α 和 b = √1− α。对于等式 (17) 所示的分布,等效采样步骤为:
考虑到这一点:如果存在随机变量 X ∼ N (μ, σ^2),则可以通过定义 X = μ + ση 来等效地从该高斯中提取 X,其中 η ∼ N (0, 1)。
我们可以进行递归以表明
上面的有限和是独立高斯随机变量的总和。平均向量 E[w_t] 保持为零,因为每个人都的均值为零。协方差矩阵(对于零均值向量)为
当 t → ∞ 时,对于任何 0 < a <1,在 t = ∞ 时的极限处,
因此,如果我们想要lim t→∞Cov[w_t] = I (因此x_t的分布将接近N (0, I),那么b =√1−a^2。现在,如果我们让a =√α,那么b =√(1−α)。这将给我们
或者等效地,
。如果您更喜欢调度程序,您可以用 α_t 替换 α。
2.3 分布q_\phi (x_t|x_0) 
通过对魔法标量的理解,我们可以谈论分布 。也就是说,如果给定 x_0,我们想知道 x_t 将如何分布
条件分布
。条件分布
由下式给出:
where
.
证明。要了解为什么这种情况,我们可以重新进行递归,但这次我们分别使用√αtxt−1和(1−αt)I作为均值和协方差。这将给我们:
因此,我们有两个高斯的总和。但是由于两个高斯的总和仍然是一个高斯的,我们只能计算它的新协方差(因为平均值保持为零)。新的协方差是
回到Eqn(22),我们可以证明递归被更新为xt−2和噪声向量εt−2的线性组合:
因此,如果我们定义
,我们可以证明
换句话说,分布
是
与链 x0→x1→ ... → x_T-1 → x_T 相比,新分布 的效用是其一次性正向扩散步骤。在正向扩散模型的每一步中,由于我们已经知道x_0并且我们假设所有子序列转换都是高斯的,我们将立即知道任何 t 的 x_t。情况可以从图 11 来理解。
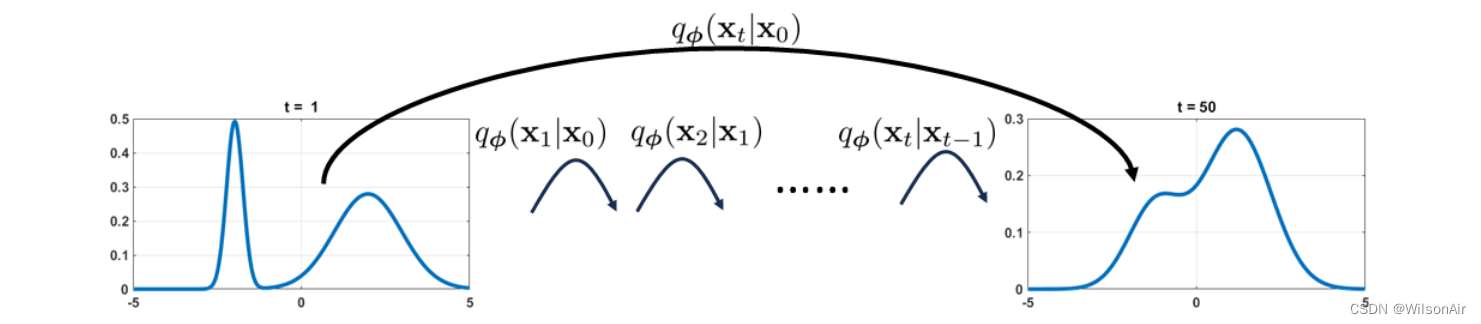
图 11:和
之间的差异。
例。对于高斯混合模型,使得
,我们可以证明时间 t 的分布为
如果您好奇概率分布 p_t 如何随时间 t 演变,我们在图 12 中展示了分布的轨迹。您可以看到,当我们在 t = 0 时,初始分布是两个高斯的混合。随着我们按照等式(26)中定义的转换取得进展,我们可以看到分布逐渐变成单个高斯 N (0, 1)。
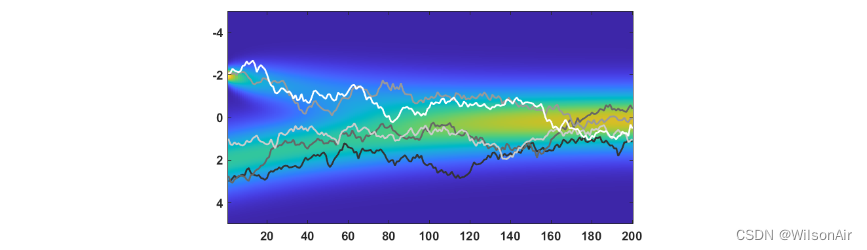
图 12:高斯混合的轨迹图,随着我们将概率分布转移到 N (0, 1) 的进展。
在同一图中,我们叠加并显示随机样本 x_t 的一些瞬时轨迹作为时间 t 的函数。我们用于生成样本的方程是
![]()
正如您所见,x_t 的轨迹或多或少遵循分布 p_t(x)。
2.4 Evidence Lower Bound
现在我们理解变分扩散模型的结构,我们可以写下 ELBO,从而训练模型。变分扩散模型的 ELBO 是
我们可以解释这个 ELBO 的含义。这里的 ELBO 由三个部分组成:
- 重建。重建项基于初始块。我们使用对数似然 p_θ (x_0|x_1) 来衡量与 p_θ 相关的神经网络可以从潜在变量 x_1 中恢复图像 x_0 的好坏。期望取自 q_φ(x_1|x_0) 的样本,它是生成 x_1 的分布。如果你感到困惑为什么我们想从 q_φ(x_1|x_0) 中抽取样本,那么只用想想样本 x_1 应该来自哪里。样本 x_1 不来自天空,由于它们是中间潜在变量,因此它们是由前向转换 q_φ(x_1|x_0) 创建的。因此,我们应该从q_φ(x_1|x_0)生成样本。
- 先验匹配。先验匹配项基于最终块。我们使用 KL 散度来衡量 q_φ(x_T |x_T -1) 和 p(x_T ) 之间的差异。第一个分布 q_φ(x_T |x_T -1) 是从 x_T-1 到 x_T 的正向转换。这是如何生成 x_T。第二个分布是 p(x_T )。由于我们的懒惰,p(x_T) 是 N (0, I)。我们希望 q_φ(x_T |x_T -1) 尽可能接近 N (0, I)。这里的样本是从 q_φ(x_T-1|x_0) 中提取的 x_T-1,因为 q_φ(x_T -1|x_0) 提供了前向样本生成过程。
- 一致性。一致性项基于转换块。有两个方向。正向转换由分布q_φ(x_t|x_t−1)决定,而反向转换由神经网络p_θ (x_t|x_t+1)决定。一致性项使用 KL 散度来衡量偏差。期望取自联合分布 q_φ(x_t−1, x_t+1|x_0) 的样本 (x_t−1, x_t+1) 取。Oh,q_φ(x_t−1,x_t+1|x_0)是什么?不用担心。我们将很快摆脱它。
此时,我们将跳过训练和推理,因为这个公式还没有准备好实现。我们将讨论更多的技巧,然后我们将讨论实现。
等式的证明 (27)。让我们定义以下符号:x_0:T = {x_0, ..., x_T } 表示从 t = 0 到 t = T 的所有状态变量的集合。我们还记得先验分布 p(x) 是图像 x_0 的分布。所以它等价于 p(x_0)。考虑到这些,我们可以证明
(第二步相当于x_0的边缘分布,通过对x_1:T的积分实现,因为 后者积分为1;第三步这里引入q_fai也相当于作者把自己的预测网络加入到分布的实现中,这也很自然;第四步在上一节关于VAE的 Evidence Lower Bound 公式 4 中有所介绍,也跟概率论与数理统计中第五版 P96:设Y是随机变量X的函数:Y=g(X)(g是连续函数). 则有 E(Y)=E[g(X)] 。有关,这里方括号内的表示g(X),即关于X的函数,期望符号的下标应该是为了表示变量X. wilson 2024.4.3)
现在,我们需要使用 Jensen 不等式,它指出对于任何随机变量 X 和任何凹函数 f ,它认为 f (E[X]) ≥ E[f(X)]。通过认识到 f (·) = log(·),我们可以证明
让我们仔细看看 p(x_0:T )。检查图 8,我们注意到如果我们想解耦 p(x_0:T ),我们应该对 x_t−1|x_t 进行调节。这导致:
对于q_φ(x_1:T |x_0),图8表明我们需要对x_t|x_t−1进行条件反射。然而,由于顺序关系,我们可以写
(这里使用q_φ来考虑前向过程 0 - T. wilson)
将Eqn(29)和Eqn(30)代入Eqn(28),可以证明
上述第一项可以进一步分解为两个期望
重建项可以简化为
我们使用了条件x_1:T |x_0等价于 x_1|x_0 的事实。
先验匹配项为
我们注意到条件期望可以简化为仅采样 x_T 和 x_T -1,因为 log[ p(x_T ) / q_φ(x_T |x_T-1) ] 仅取决于 x_T 和 x_T -1。
最后,我们查看乘积项。我们证明
通过将 p(x_0|x_1) 与 p_θ (x_0|x_1) 和 p(x_t|x_t+1) 替换为 p_θ (x_t | x_t+1),我们完成。
(最后一项即为一致性项,用来保证前后转换的一致性。Wilson)
2.5 Rewrite the Consistency Term
上述变化扩散模型的夜间是我们需要从联合分布 q_φ(x_t−1, x_t+1|x_0) 中抽取样本 (x_t−1, x_t+1)。我们不知道q_φ(x_t−1,x_t+1|x_0)是什么!当然,它是一个高斯的,但我们仍然需要使用未来的样本x_t+1来绘制当前样本x_t。这是奇怪的,不有趣。
检查一致性项,我们注意到 q_φ(x_t|x_t−1) 和 p_θ (x_t|x_t+1) 沿两个相反的方向移动。因此,我们不可避免地需要使用x_t−1和x_t+1。我们需要问的问题是:我们是否可以提出一些东西,这样我们不需要处理两个相反的方向,而我们能够检查一致性?(这是重写一致性项目的动机。 Wilson)
因此,这里是称为贝叶斯定理的简单技巧。
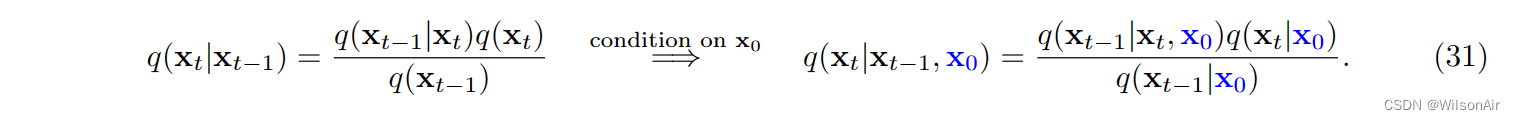
随着条件顺序的这种变化,我们可以通过添加更多条件变量 x_0 将 q(x_t|x_t−1, x_0) 切换到 q(x_t−1|x_t, x_0)。方向 q(x_t−1|x_t, x_0) 现在平行于 p_θ (x_t−1|x_t),如图 13 所示。因此,如果我们想重写一致性项,一个自然的选择是计算 q_φ(x_t−1|x_t, x_0) 和 p_θ (x_t−1|x_t) 之间的 KL 散度。
(所以现在的这个一致性是由贝叶斯定理引出来的,很顺理成章哇!Wilson)
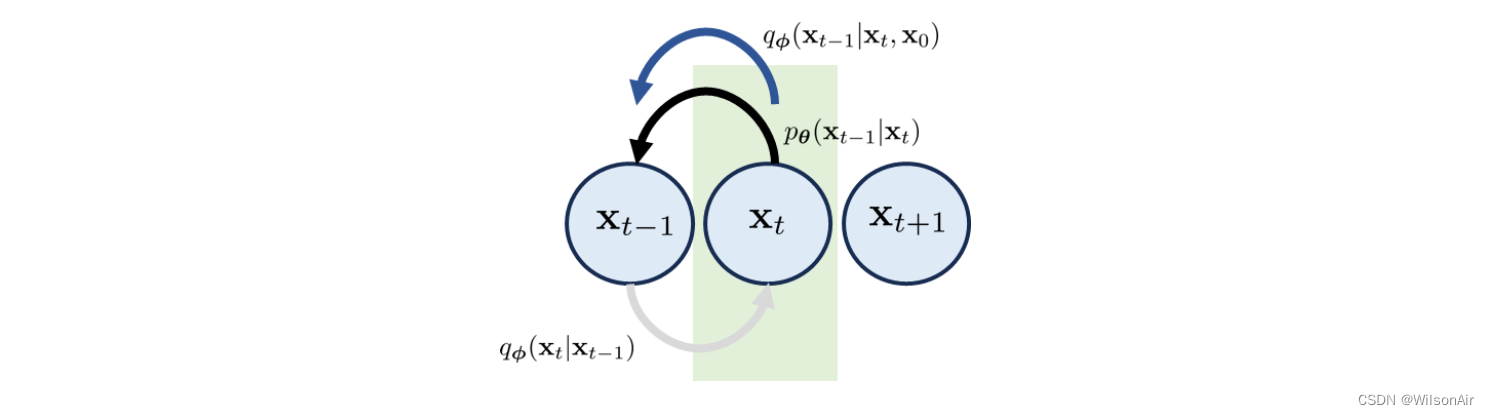
图13:如果我们考虑Eqn(31)中的贝叶斯定理,我们可以定义一个方向平行于p_θ (x_t−1|x_t, x_0)的分布q_φ(x_t−1|x_t, x_0)。
如果我们设法经过几个(无聊)代数推导,我们可以证明 ELBO 现在是:
变分扩散模型的 ELBO 是:
让我们快速做出三种解释:
- 重建。新的重建项与以前相同。我们仍然最大化对数似然。
- 先验匹配。新的先验匹配被简化为 q_φ(x_T |x_0) 和 p(x_T ) 之间的 KL 散度。变化是由于我们现在以 x_0 为条件。因此,不需要从 q_φ(x_T-1|x_0) 中抽取样本并采用期望。(这里是合并了当中的采样过程,从而使得x_T可以直接由x_0与正态分布的加权和。Wilson)
- 一致性。新的一致性项目与之前的项目在两种方面不同。
- 首先,运行索引 t 从 t = 2 开始,并在 t = T 结束。以前从 t = 1 到 t = T - 1。与此相伴是分布匹配,现在在 q_φ(x_t−1|x_t, x_0) 和 p_θ (x_t−1|x_t) 之间。
- 因此,我们没有使用前向转换来匹配反向转换,而是使用 q_φ 来构建反向转换并使用它来与 p_θ 匹配。(相当于重写了式子30,由反向的变为x_0出发。Wilson)
等式 (32) 的证明。我们从Eqn(28)开始,表明:
让我们考虑第二项:(就是把式子31的贝叶斯定理代入进来,Wilson)
其中最后一个方程使用的事实包括:对于任何序列 a_1 , ... , a_T ,我们有
回到等式 (33),我们可以看到
其中我们在分子和分母中取消 q_φ(x_1|x_0),因为对于任何正常数 a、b 和 c,log a/b + log b/c = log a/c。这将给我们
最后一项是
最后,将 p(x_t−1|x_t) 替换为 p_θ (x_t−1|x_t),将 p(x_0|x_1) 替换为 p_θ (x_0|x_1)。得证!
最后再贴一遍ELBO的公式:
2.6 Derivation of q_φ(x_t−1|x_t, x_0)
现在我们知道变分扩散模型的新 ELBO,我们应该花一些时间讨论其核心组件,即 q_φ(x_t−1|x_t, x_0)。简而言之,我们想要展示的是
- q_φ(x_t−1|x_t, x_0) 不像你认为的那样疯狂。它仍然是一个高斯。
- 由于它是一个高斯的,它完全由均值和协方差来表征。事实证明
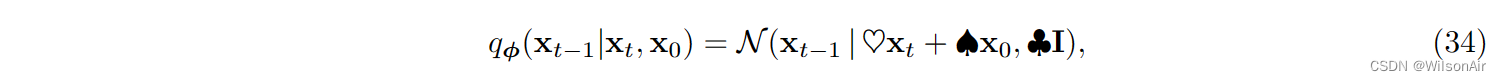
对于某些神奇标量 ♡、♠ 和 ♣ 定义如下。
分布 q_φ(x_t−1|x_t, x_0) 采用以下形式:
其中:
Eqn(35)的有趣部分是 q_φ(x_t−1|x_t, x_0) 完全由 x_t 和 x_0 表征。估计均值和方差不需要神经网络!(你可以将其与VAE进行比较,其中需要一个网络。)由于不需要网络,所以真的没有“学习”什么东西。如果我们知道 x_t 和 x_0,则自动确定分布 q_φ(x_t−1|x_t, x_0)。没有猜测,没有估计,什么都没有。
这里的实现很重要。如果我们查看一致性项,它是许多 KL 散度项的总和,其中第 t 个项是
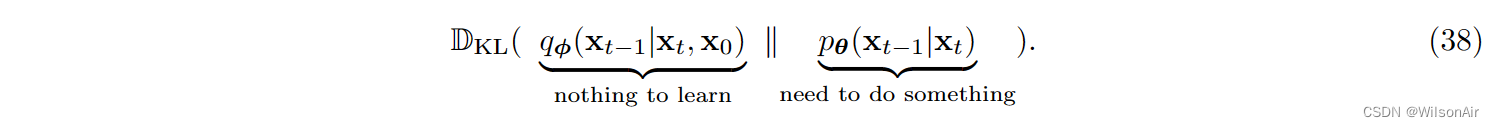
正如我们刚才所说,与 q_φ(x_t−1|x_t, x_0) 无关。但是我们需要对 p_θ (x_t−1|x_t) 做一些事情,以便我们可以计算 KL 散度。
因此,我们应该做什么。我们知道 q_φ(x_t−1|x_t, x_0) 是高斯的。是的,没有开玩笑。我们没有理由为什么它是高斯的。但是由于 p_θ 是我们可以选择的分布,我们当然应该选择更容易的东西。(其实高斯分布有许多优秀的性质可以用来模拟真实世界,其次,他参数量少,建模很方便,这应该是最大的选择理由,Wilson) 。如果我们想快速计算 KL 散度,那么显然我们需要假设 p_θ (x_t−1|x_t) 也是高斯的。为此,我们选择
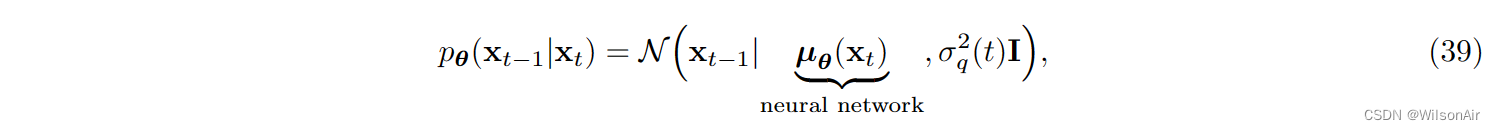
我们假设可以使用神经网络确定平均向量。至于方差,我们选择方差为 。这与等式 (37) 相同!因此,如果我们用 p_θ (x_t−1|x_t) 并排放置 Eqn (35),我们注意到两者之间存在平行关系:
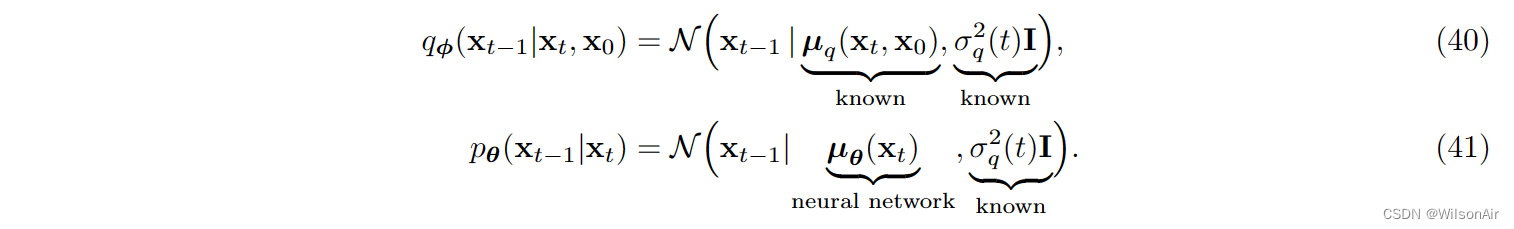
因此,KL散度简化为
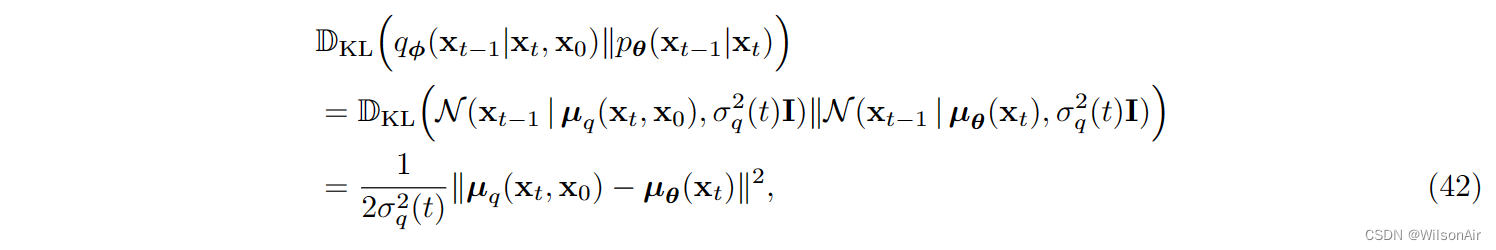
其中我们使用了两个相同方差高斯之间的 KL 散度只是两个均值向量之间的欧氏距离平方这一事实。
如果我们回到等式 (32) 中 ELBO 的定义,我们可以将其重写为
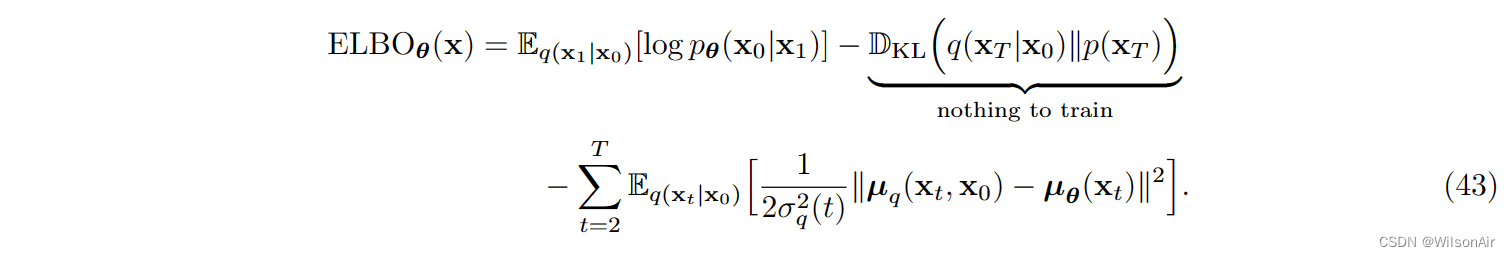
一些观察结果很有趣:
- 我们删除了所有下标 φ,因为只要我们知道 x_0,q 就完全被描述为。我们只是在每个 x_1, ..., x_T 中添加(不同级别的)白噪声。这将为我们提供一个 ELBO,它只需要我们对 θ 进行优化。
- 参数 θ 是通过网络 μ_θ (x_t) 实现的。它是 μ_θ (x_t) 的网络权重。
- q(x_t|x_0) 的采样是根据 Eqn (21) 完成的,它指出
。
- 给定 x_t ∼ q(x_t|x_0),我们可以计算 log p_θ (x_0|x_1),它只是 log N (x_0 | μ_θ (x_1), σ^2_q (1)I)。因此,一旦我们知道 x1,我们就可以将其发送到网络 μ_θ (x_1) 以返回平均估计。然后将使用平均估计来计算可能性。
在我们进一步下降之前,让我们通过讨论如何确定 Eqn (35) 来完成故事。
等式 (35) 的证明。使用Eqn(31)中所述的贝叶斯定理,如果我们评估以下高斯函数的乘积,则可以确定q(x_t−1|x_t, x_0)
为简单起见,我们将处理向量是标量。那么上述高斯函数的乘积将变成
我们考虑以下映射:
考虑一个二次函数
我们知道,无论我们如何重新排列术语,得到的函数仍然是一个二次方程。f (y) 的最小化器是结果高斯的平均值。因此,我们可以计算 f 的导数并表明
设置 f'(y) = 0 产生
我们注意到
。所以,
类似地,对于方差,我们可以检查曲率 f ''(y)。我们很容易证明
取倒数将给我们
2.7 Training and Inference
Eqn (43) 中的 ELBO 表明我们需要找到一个可以以某种方式最小化这种损失的网络 μ_θ:
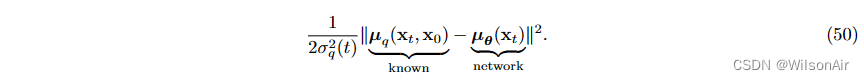
但是“去噪”概念来自哪里。要了解这一点,我们从 Eqn (36) 中回忆,即
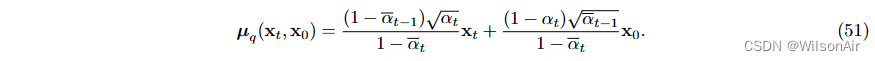
由于 μ_θ 是我们的设计,我们没有理由不能将其定义为更方便的东西。所以这里是一个选项:

将Eqn(51)和Eqn(52)代入Eqn(50)将给我们
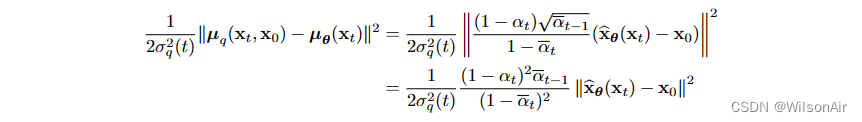
因此ELBO可以简化为
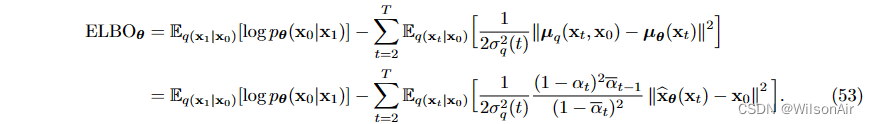
第一项是
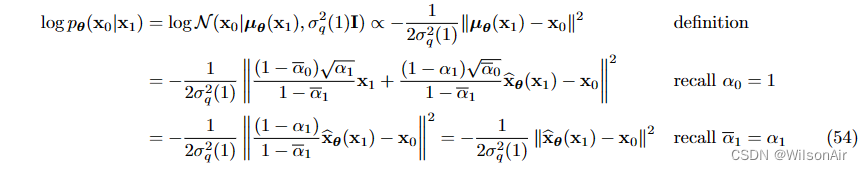
将 Eqn (54) 代入 Eqn (53) 将简化 ELBO 作为
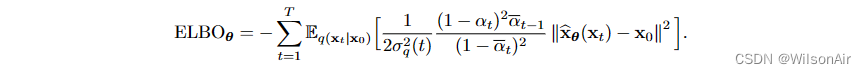
因此,神经网络的训练归结为一个简单的损失函数:
去噪扩散概率模型的损失函数:
Eqn (55)中定义的损失函数非常直观。忽略特定 x_t 的常数和期望,感兴趣的主要主题是
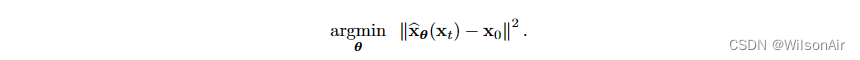
这不仅是一个去噪问题,因为我们需要找到一个网络 ,使去噪后的图像
将接近地面真值x_0。这使得它不是一个典型的去噪器:
- Eq(x_t|x_0):我们不会尝试去噪任何随机噪声图像。相反,我们仔细选择噪声图像是
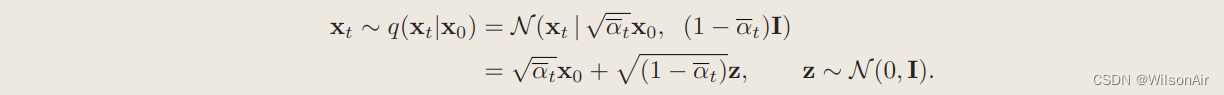
在这里,通过“谨慎”,这意味着我们注入图像的噪声量被仔细控制。
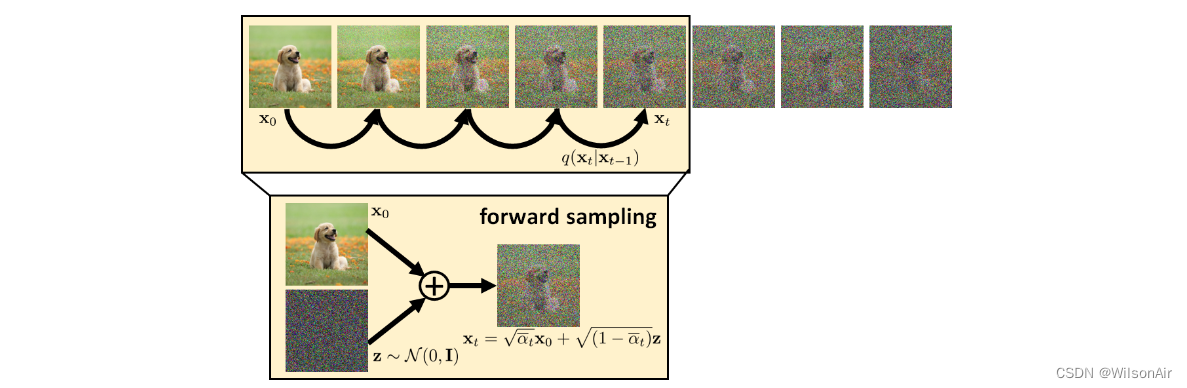
图 14:前向采样过程。前向采样过程最初是一系列操作。但是,如果我们假设高斯,那么我们可以将采样过程简化为一步数据生成。
-
: 我们不会对所有步骤平等地加权去噪损失。相反,有一个调度器来控制每个去噪损失的相对强调。但是,为简单起见,我们可以删除这些。它的影响很小。(通过一个batch 来训练的时候,多个不同步骤之间的损失加权?Wilson)
-
: 求和能够被均匀分布 t ~ Uniform[1,T] 所代替。
训练去噪扩散概率模型。(版本:预测图像)对于训练数据集中的每个图像 x_0:
- 重复以下步骤直到收敛。
- 选择一个随机时间戳 t ~ Uniform[1,T]。
- 绘制样本
,即:
- 取梯度下降步骤
- 你可以批量做到这一点,就像你如何训练任何其他神经网络一样。请注意,在这里,您正在为所有噪声条件训练一个去噪网络
。
一旦训练了去噪器 ,我们就可以将其应用于推理。推理是关于从状态 x_T , x_T -1, ..., x_1 序列上的分布 p_θ (x_t−1|x_t) 中采样图像。因为它是相反的扩散过程,我们需要通过递归执行它:
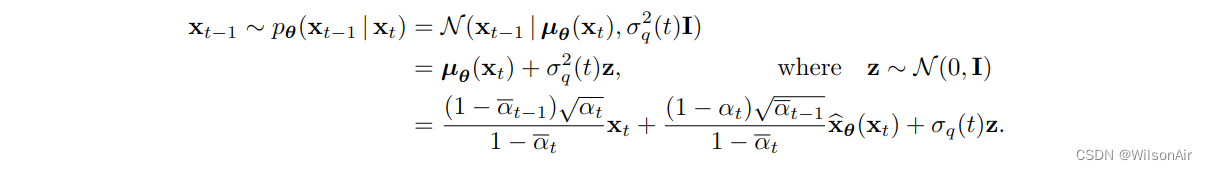
(第二项中学习的是x_0的分布,x_t-1完全由x_0,x_t 获得。 Wilson)
这导致以下推理算法。
降噪认扩散概率模型的推理。(版本:预测图像)
• 你给我们一个白噪声向量 x_T ∼ N (0, I)。
• 对 t = T, T−1 , ...,1。重复以下内容。
• 我们使用经过训练的降噪器计算
。
• 根据以下更新
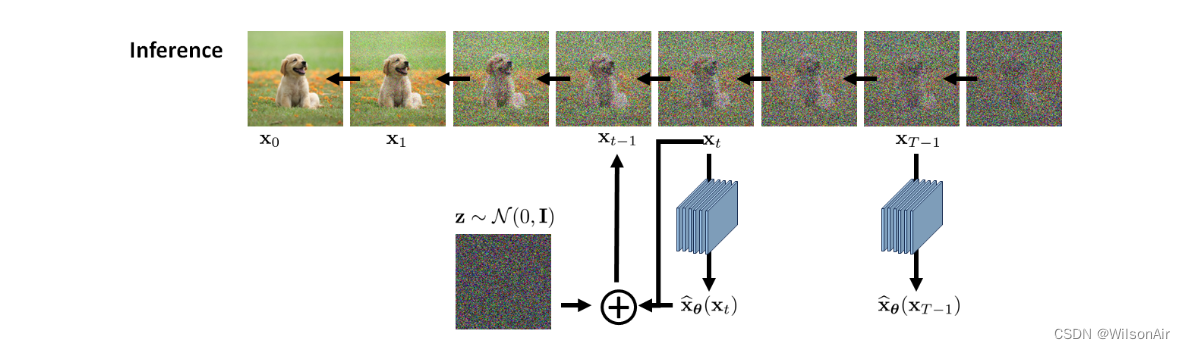
图 16:去噪扩散概率模型的推理。
2.8 基于噪声向量的推导
如果你熟悉去噪文献,你可能知道算法的残差类型预测噪声而不是信号。同样的逻辑也适用于去噪扩散,我们可以学习预测噪音。要了解为什么这种情况,我们考虑 Eqn (24)。如果我们重新排列项目我们将获得的
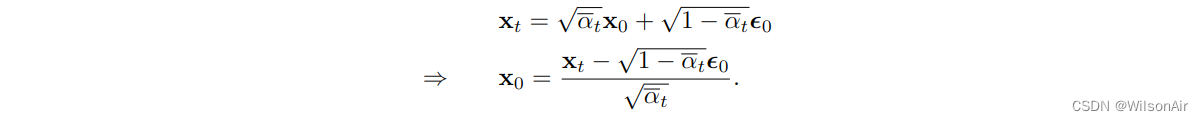
将其代入 μ_q (x_t, x_0),我们可以证明
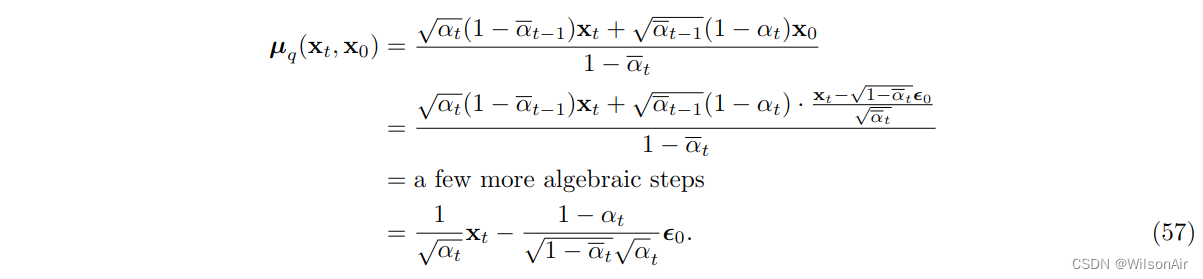
因此,如果我们可以设计我们的均值估计器 μ_θ ,我们可以自由选择它与以下形式匹配:
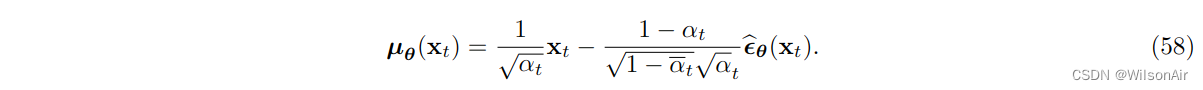
将等式 (57) 和 Eqn (58) 代入 Eqn (50) 将为我们提供一个新的 ELBO
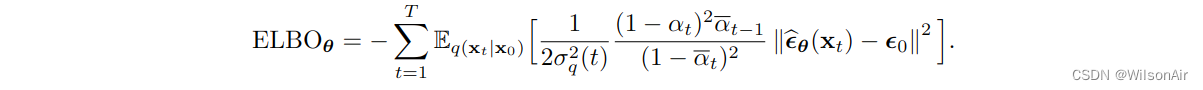
因此,如果您给我们 x_t,我们将返回您预测的噪声。这将为我们提供另一种训练方案
训练降噪扩散概率模型(预测噪声版本)。对于训练数据集中的每个图像 x_0:
- 重复以下步骤直到收敛。
- 选择一个随机时间戳 t ~ Uniform[1,T]。
- 绘制样本
,即:
- 取梯度下降步骤
因此,推理步骤可以通过
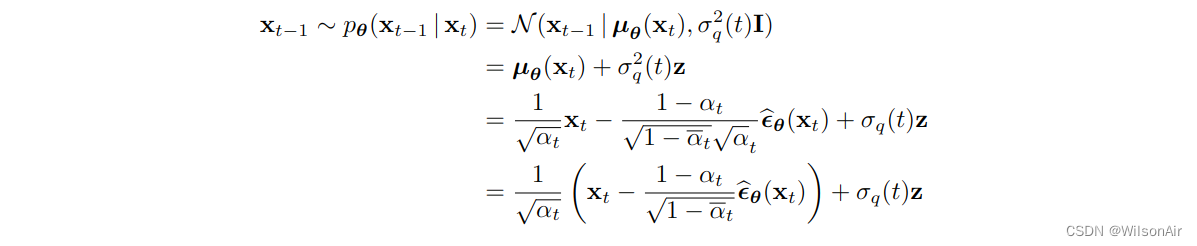
总结在这里,我们有
降噪扩散概率模型的推理。(版本预测噪声):
• 你给我们一个白噪声向量 x_T ∼ N (0, I)。
• 对 t = T, T−1 , ...,1。重复以下内容。
• 我们使用经过训练的降噪器计算
。
• 根据以下更新
2.9 Inversion by Direct Denoising (InDI)
如果我们查看 DDPM 方程,我们将看到更新 Eqn (56) 采用以下形式:
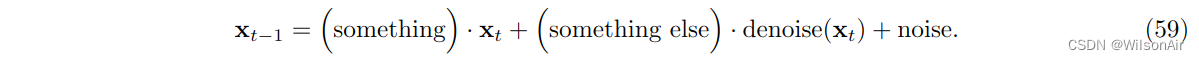
换句话说,第 (t − 1) 个估计是三个项的线性组合:当前估计 x_t、去噪版本 denoise(x_t) 和噪声项。当前的估计和噪声项很容易理解。但是“denoise”是什么。Delbracio 和 Milanfar [6] 的一个有趣论文从纯去噪的角度研究了生成扩散模型。事实证明,这种令人惊讶的简单观点与其他更高级的扩散模型以某种良好的方式一致。
什么是 denoise(x_t)。去噪是一种通用程序,可以从噪声图像中去除噪声。在统计信号处理的早期,一个标准的教科书问题是推导出白噪声的最优去噪器。给定观察模型
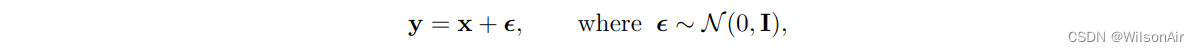
你能构造一个估计量g(·),使均方误差最小化。我们将跳过这个经典问题的解决方案的推导,因为您可以在任何概率教科书中找到它,例如 [7, 章 8]。解决方案是
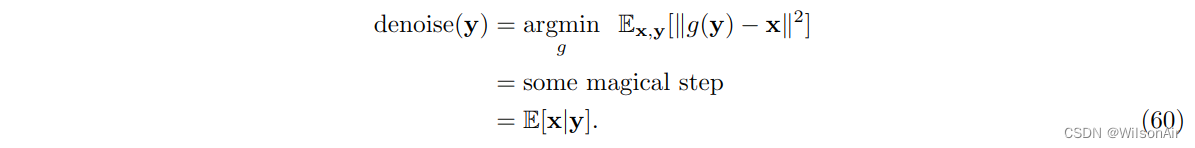
因此,回到我们的问题:如果我们假设
![]()
那么显然去噪器是后验分布的条件期望:
![]()
因此,如果我们给出分布 p_θ (x_t−1|x_t),那么最优降噪器只是该分布的条件期望。这种降噪器称为最小均方误差 (MMSE) 降噪器。MMSE降噪器不是“最佳”降噪器;它只是均方误差的最佳降噪器。由于均方误差不是图像质量的一个很好的度量,因此最小化 MSE 不一定给我们更好的图像。然而,人们喜欢MMSE 这样的降噪器,因为它们很容易推导。
增量去噪步骤。如果您理解 MMSE 降噪器等价于后验分布的条件期望,您将欣赏增量去噪。这是它是如何工作的。假设我们有一个干净的图像x_0和一个噪声图像 y。我们的目标是通过简单的方程形成 x_0 和 y 的线性组合
![]()
现在,考虑时间 t 之前的一个小步骤 τ 。以下结果,如 [6] 所示,提供了一些有用的实用程序:
令 0 ≤ τ < t ≤ 1 ,并假设 x_t = (1 − t)x_0 + t_y,则认为:
如果我们将 定义为左侧,将 x_t 替换为
,并将 E[x_0|x_t] 写为
,则上述方程将变为
(64)
其中 τ 是时间的一个小步骤。
Eqn (64) 给了我们一个推理步骤。如果您告诉我们降噪器并假设您从噪声图像 y 开始,那么我们可以迭代地应用 Eqn (64) 来检索图像 ,
, ... ,
.
Training。迭代方案的训练需要一个生成去噪(x_t)的去噪器。为此,我们可以训练神经网络denoise_θ (其中θ表示网络权重):
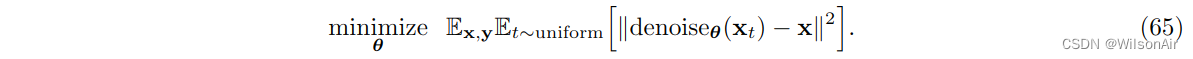
在这里,分布“t ∼ uniform”指定时间步长 t 是从给定分布中采样的。因此,我们正在为所有时间步 t 训练一个降噪器。当您使用来自训练数据集的一对嘈杂和干净的图像时,通常会满足期望 (x, y)。训练后,我们可以通过 Eqn (64) 执行增量更新。
与去噪分数匹配连接。尽管我们还没有讨论分数匹配(这将在下一节中介绍),但上述迭代去噪过程的一个有趣事实是它与去噪分数匹配有关。在高层次上,我们可以将迭代重写为
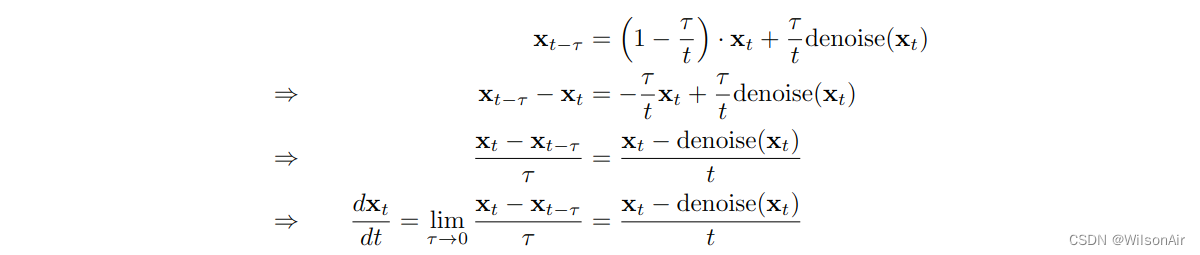
这是一个常微分方程 (ODE)。如果我们让 x_t = x+tε 使得 x_t 中的噪声水平为 ,那么我们可以使用文献中的几个结果来证明

因此,增量去噪迭代等价于去噪分数匹配,至少在由 ODE 确定的极限情况下。
添加随机步骤。上述增量去噪迭代可以配备随机扰动。对于推理步骤,我们可以定义一系列噪声水平 {σ_t | 0 ≤ t ≤ 1},并定义
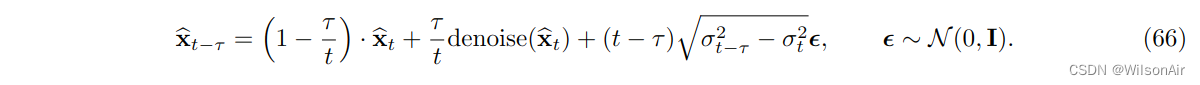
作为或训练,可以通过
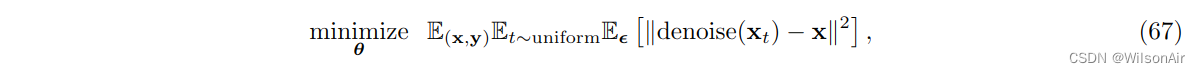
其中 。
祝贺!我们完成了。这是关于DDPM的一切。
DDPM的文献正在迅速爆炸。Sohl-Dickstein等人[10]和Ho等人[4]的原始论文是理解主题的必须阅读。对于更“用户友好的”版本,我们发现罗的教程非常有用[11]。一些后续工作被高度引用,包括Song等人[12]去噪扩散隐式模型。在应用方面,人们一直在使用各种图像合成应用使用DDPM,例如[13,14]。
[4] J. Ho, A. Jain, and P. Abbeel, "Denoising diffusion probabilistic models," in NeurIPS, 2020. https: //arxiv.org/abs/2006.11239.
[6] DELBRACIO M, MILANFAR P. Inversion by Direct Iteration: An Alternative to Denoising Diffusion for Image Restoration[J]. 2023.
[10] J. Sohl-Dickstein, E. Weiss, N. Maheswaranathan, and S. Ganguli, "Deep unsupervised learning using nonequilibrium thermodynamics," in ICML, vol. 37, pp. 2256–2265, 2015. https://arxiv.org/abs/ 1503.03585.
[11] C. Luo, "Understanding diffusion models: A unified perspective," 2022. https://arxiv.org/abs/ 2208.11970.
[12] J. Song, C. Meng, and S. Ermon, "Denoising diffusion implicit models," in ICLR, 2023. https:// openreview.net/forum?id=St1giarCHLP.
[13] R. Rombach, A. Blattmann, D. Lorenz, P. Esser, and B. Ommer, "High-resolution image synthesis with latent diffusion models," in CVPR, pp. 10684–10695, 2022. https://arxiv.org/abs/2112.10752.
[14] C. Saharia, W. Chan, S. Saxena, L. Li, J. Whang, E. L. Denton, K. Ghasemipour, R. Gontijo Lopes, B. Karagol Ayan, T. Salimans, J. Ho, D. J. Fleet, and M. Norouzi, "Photorealistic text-to-image diffusion models with deep language understanding," in NeurIPS, vol. 35, pp. 36479–36494, 2022. https: //arxiv.org/abs/2205.11487.







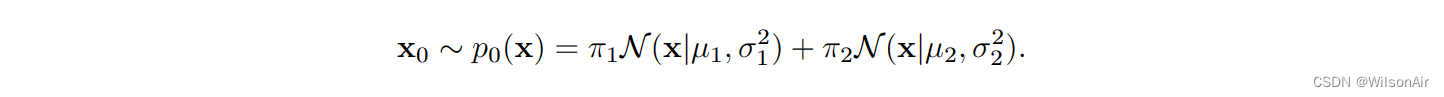
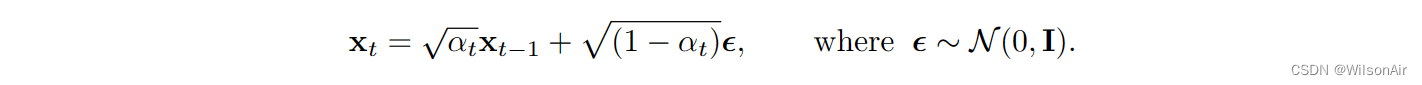
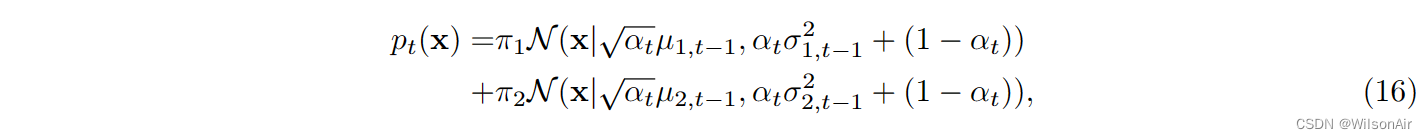
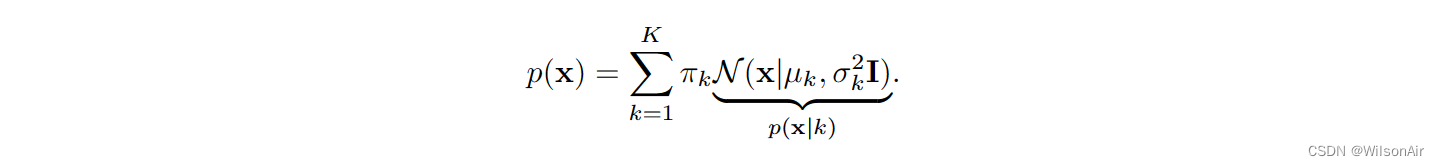
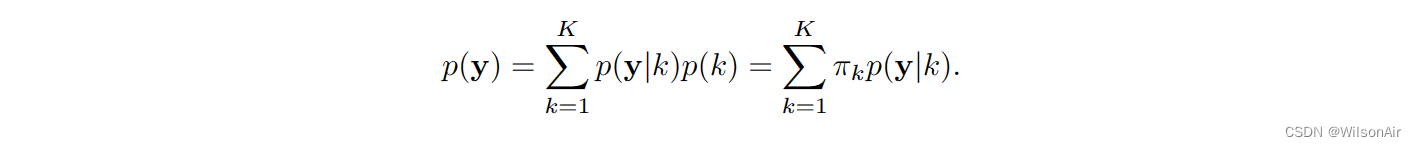
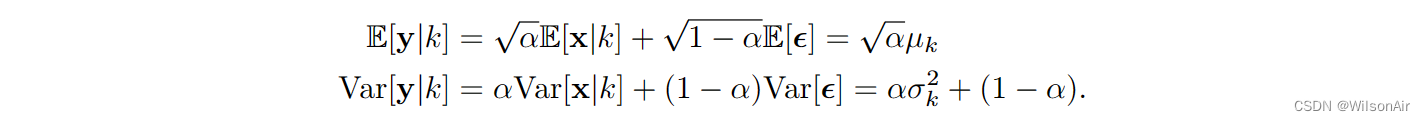
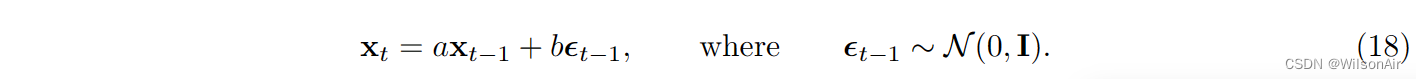
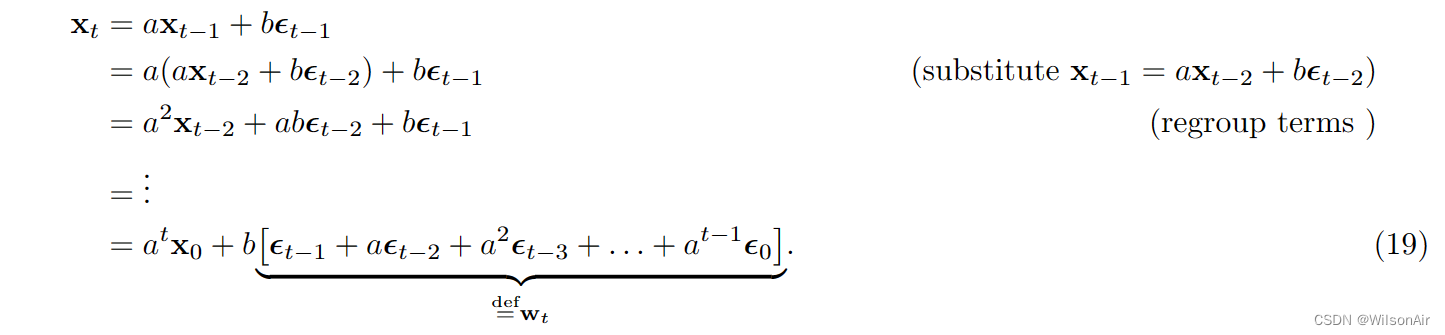
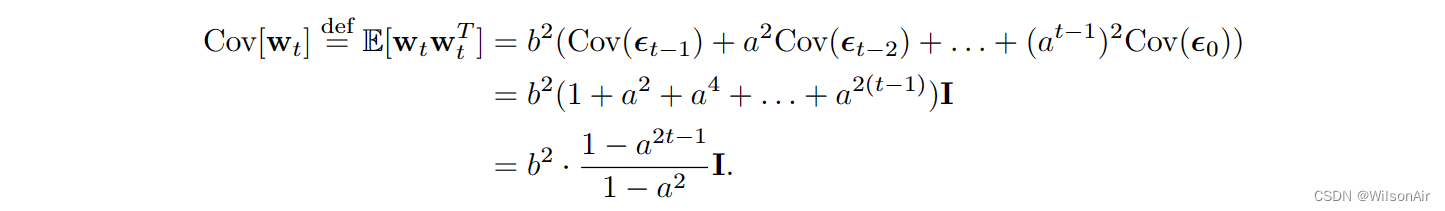
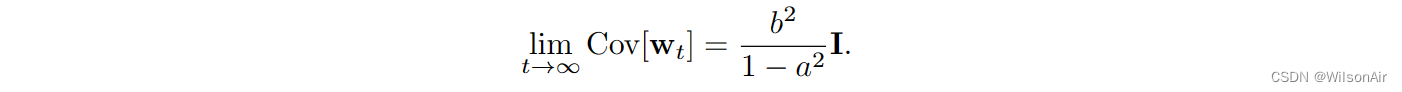
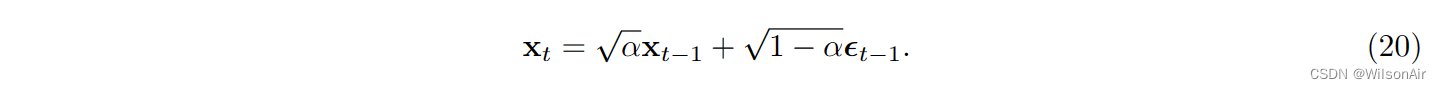
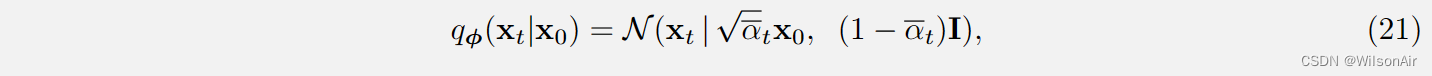
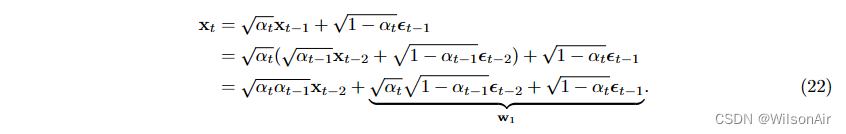
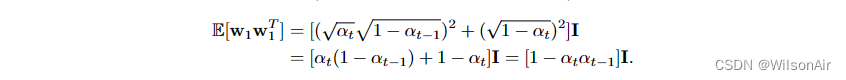
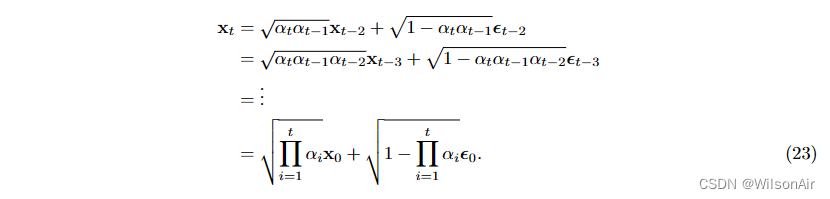
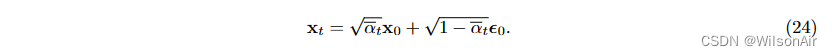
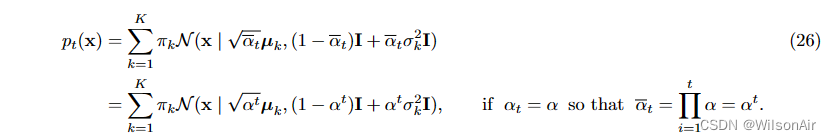


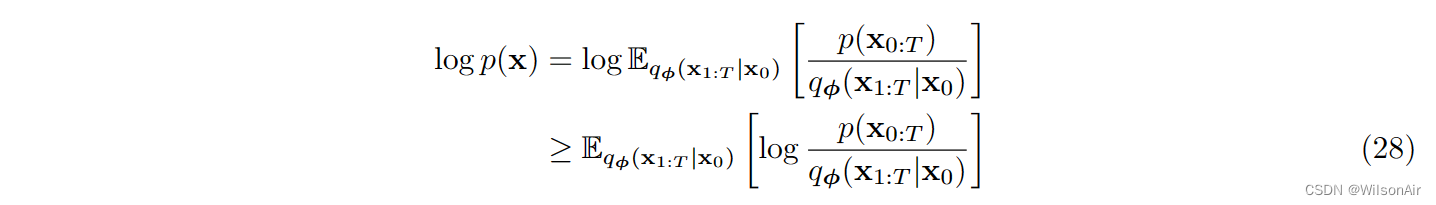
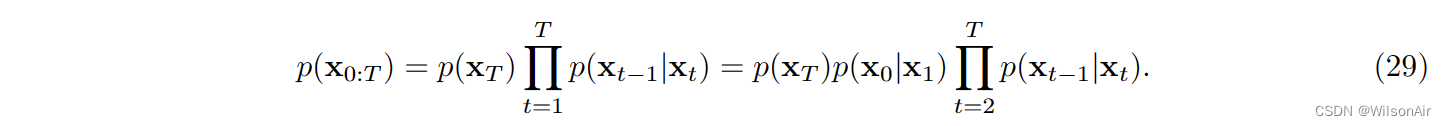
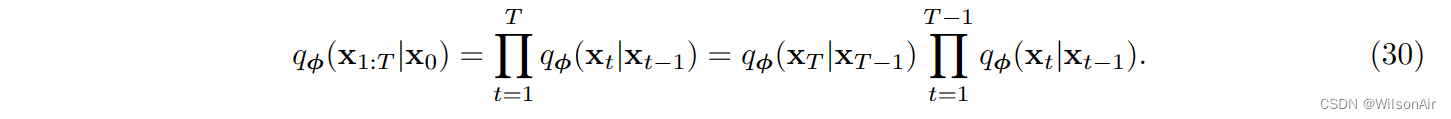
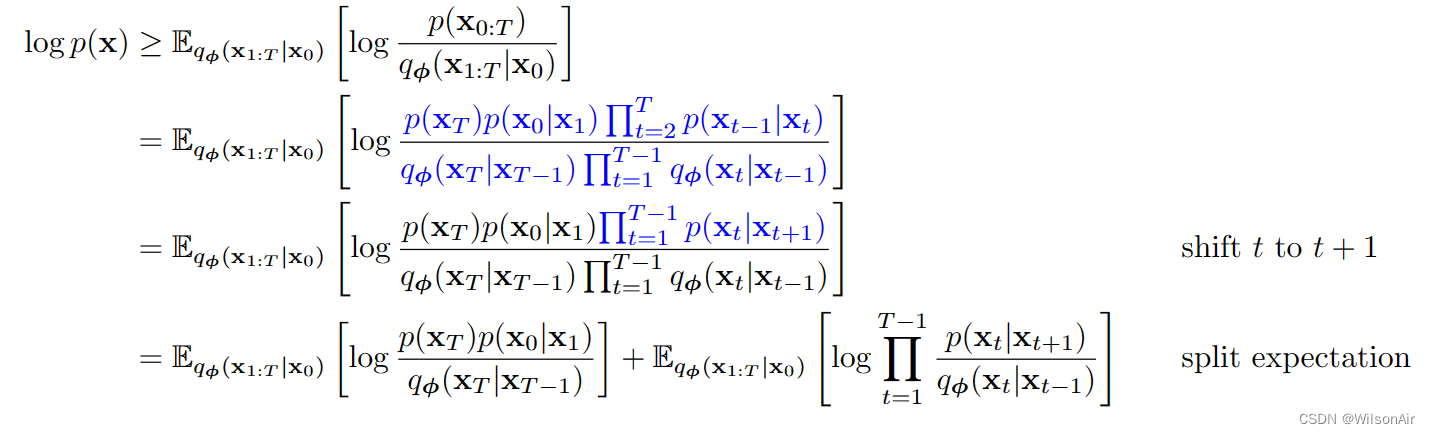
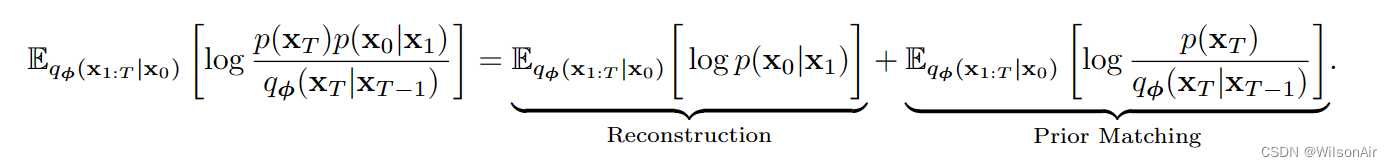
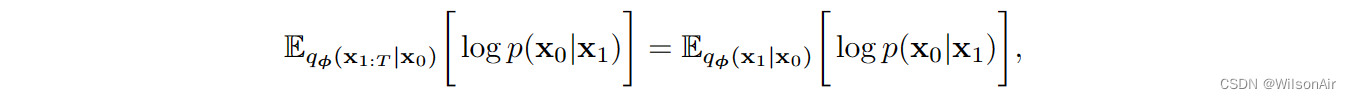
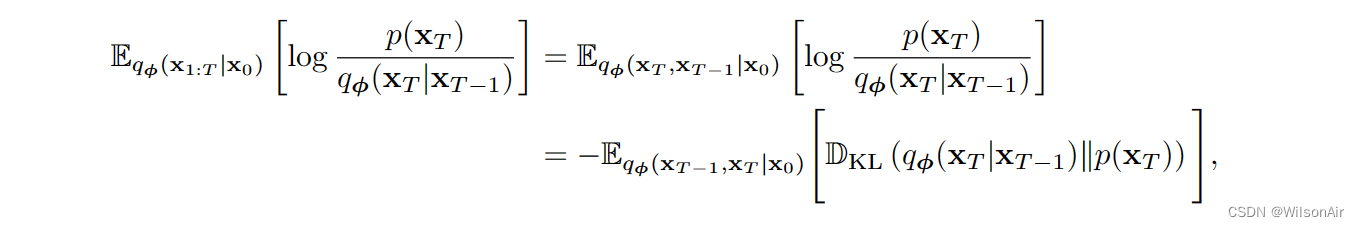
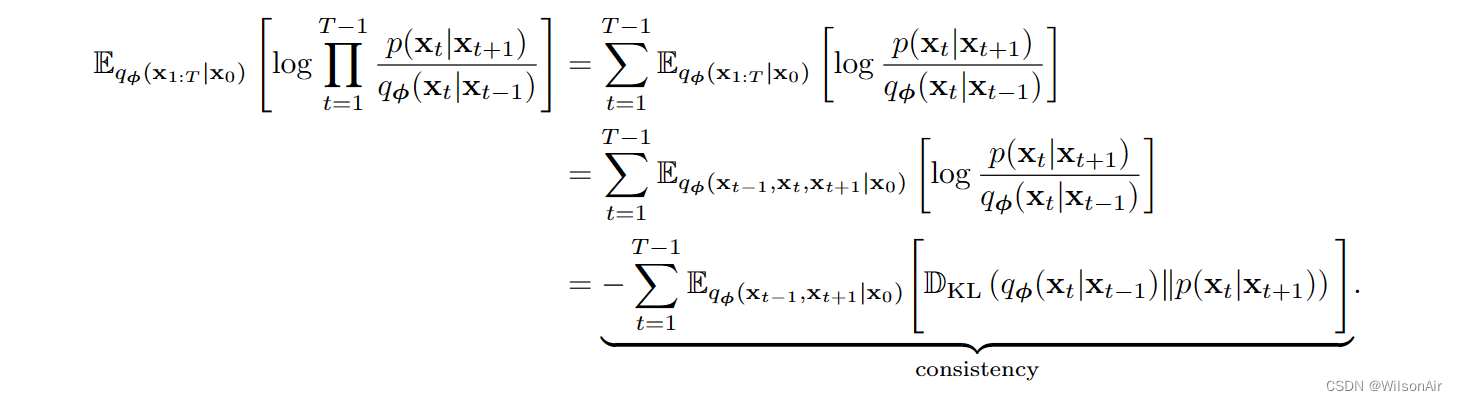
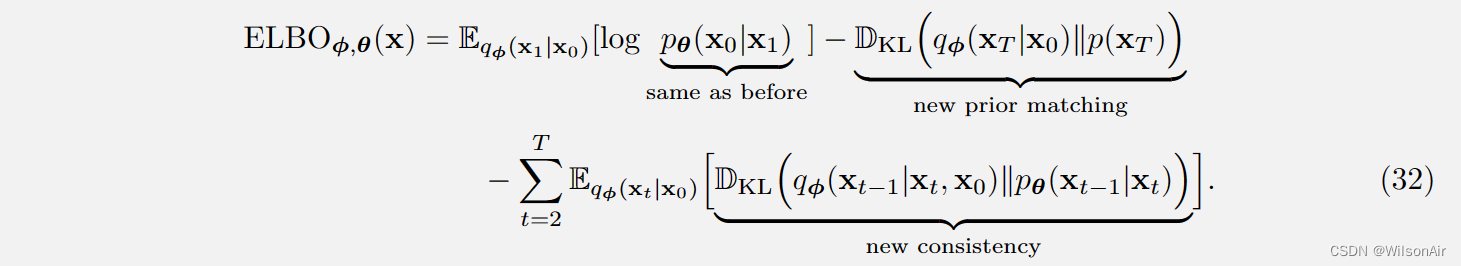
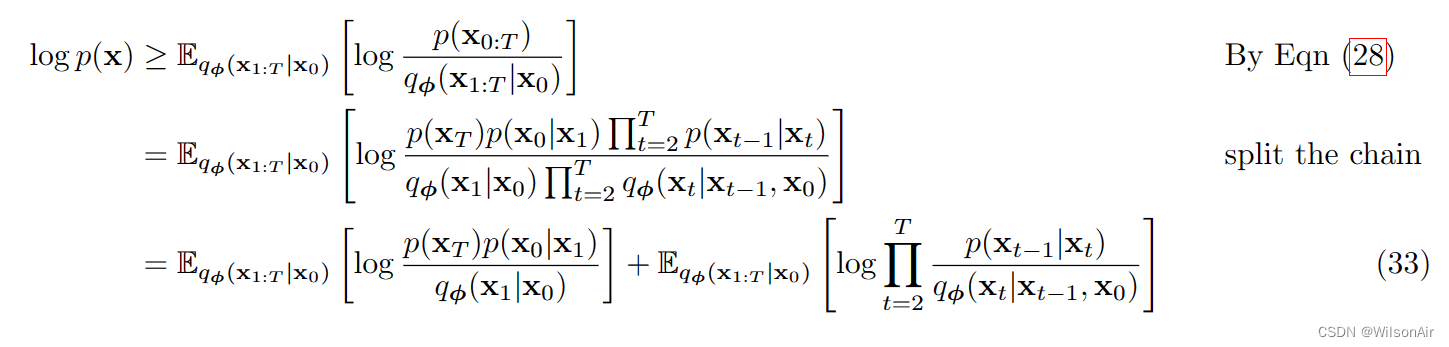
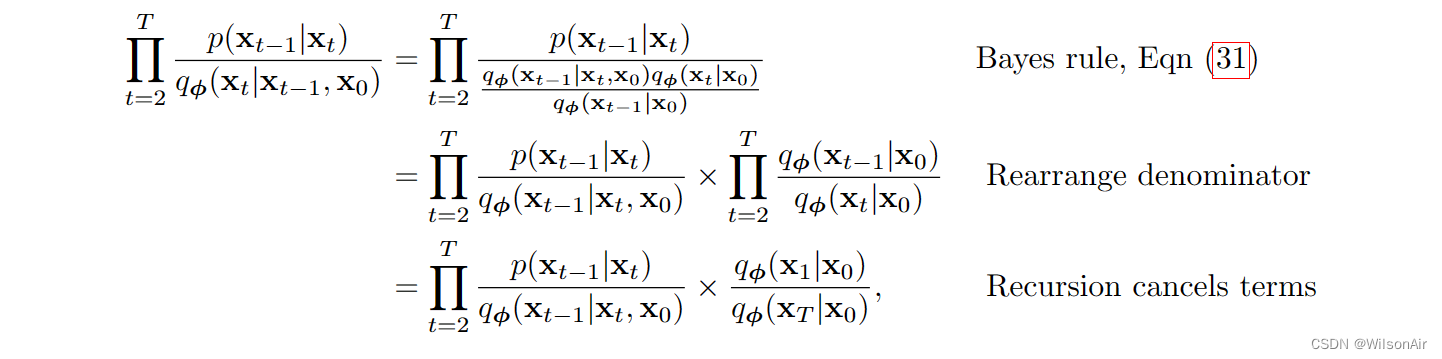
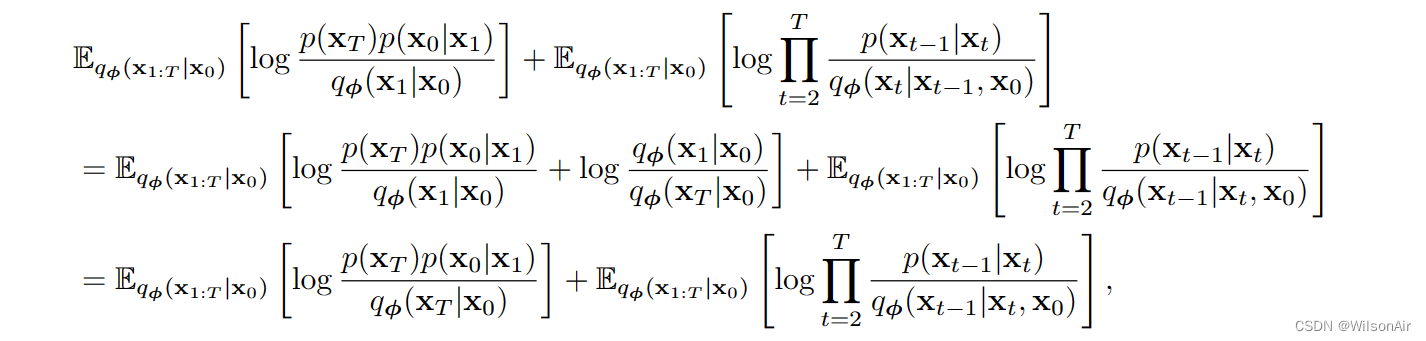
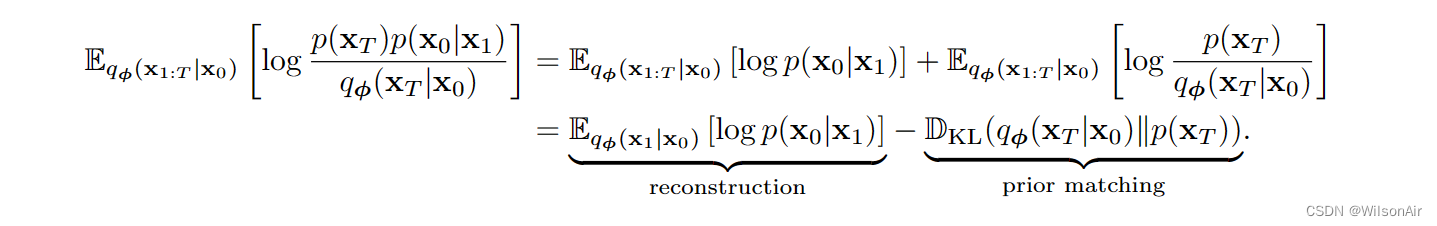
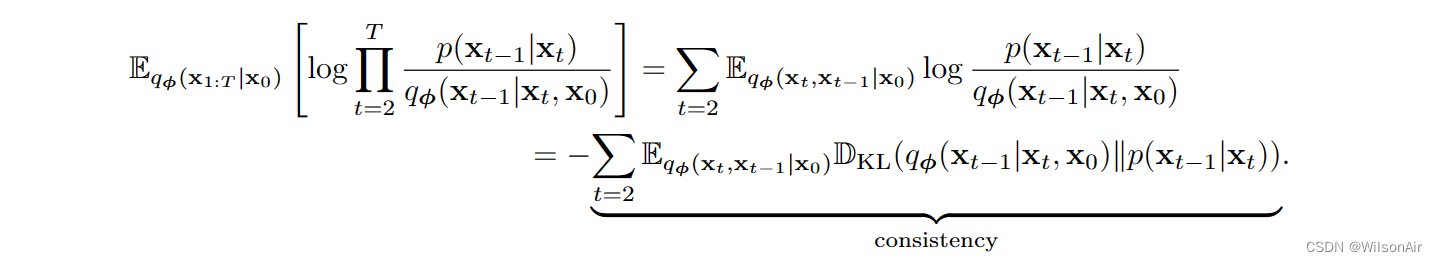
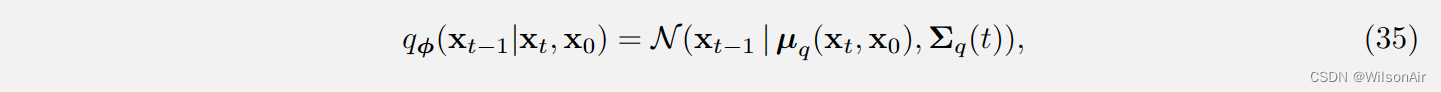
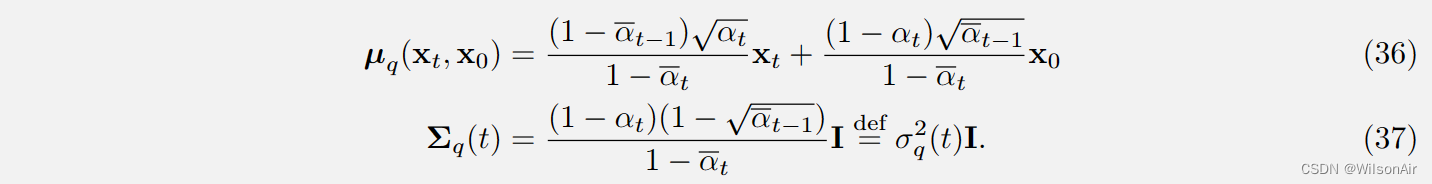
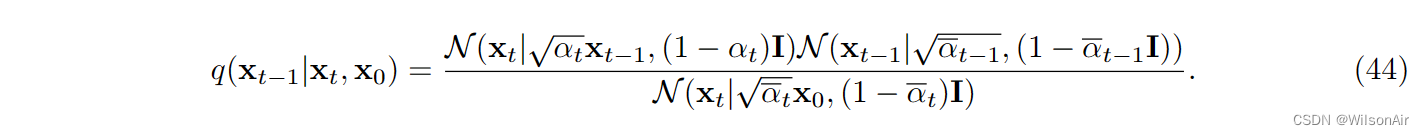
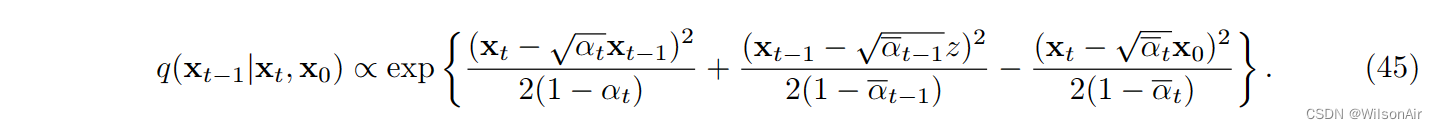
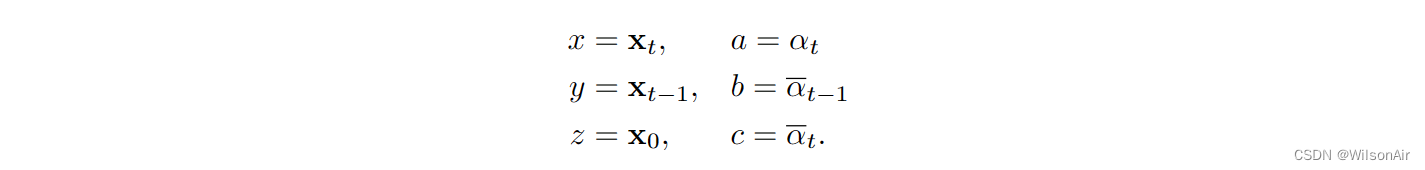
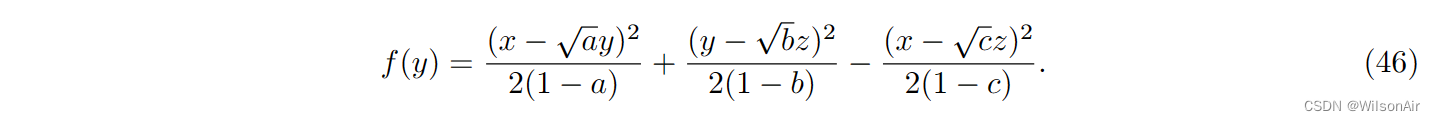
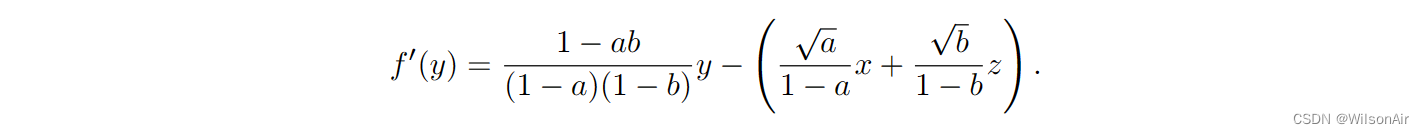
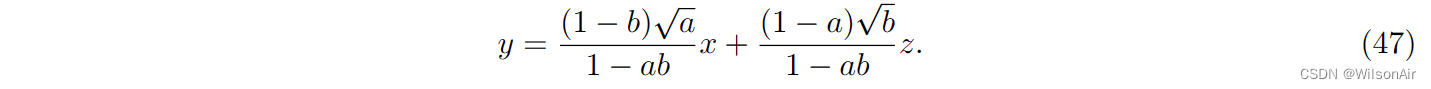
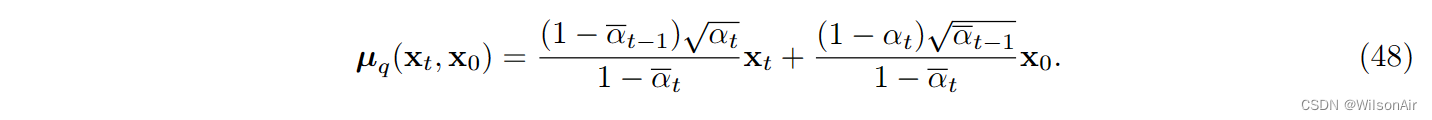
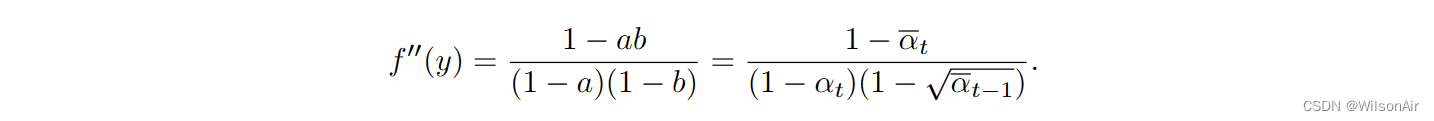
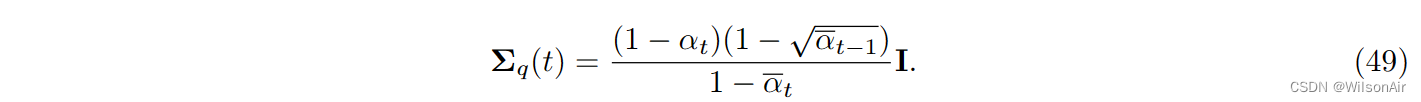
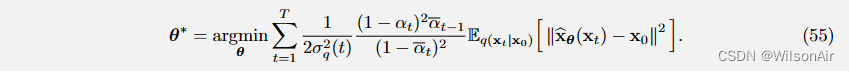
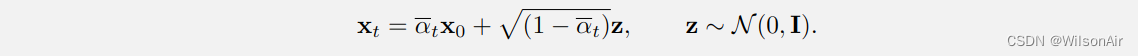
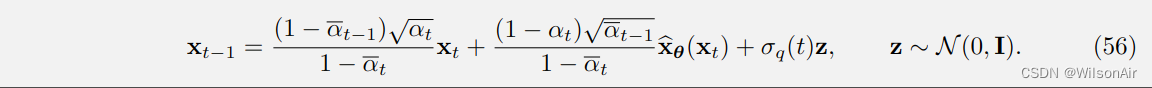
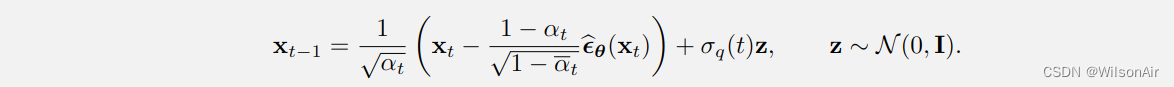
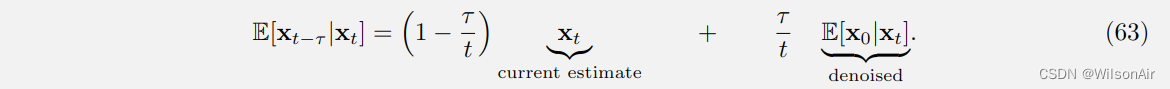














 356
356











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








